算数の記述問題を解くポイント〜グラフや図を積極的に描く・記述を意識した学び・思考力を深めて学力アップ・矢印やメモ書きで簡単に表現・「考えていること」を明確化〜｜中学受験・算数

前回は「算数の「しっかりした思考力」を育てる勉強法〜複数の視点・計算量を減らす戦略・棒グラフなどを描く姿勢・記述問題への対応・小学生らしい姿勢でしっかり描く〜」の話でした。

算数の記述問題を解くポイント：グラフや図を積極的に描く

算数の問題を色々な角度から考えることは、応用力や難問に対する力を磨きます。

それは多角的な視点から見ることになり、複眼的にも考えるようになります。

算数、あるいは中学以降の数学において「複眼的思考」は非常に大事なことです。

志望校が「答えのみ」を求める問題が多い場合でも、「記述式」を意識して学ぶのが良いでしょう。

「記述は難しい」と感じる方がいるかもしれません。

難しく考えすぎず、立式する際は多少の説明文を入れるようにしましょう。

そして、最も大事なことは「図やグラフを積極的に描くこと」です。

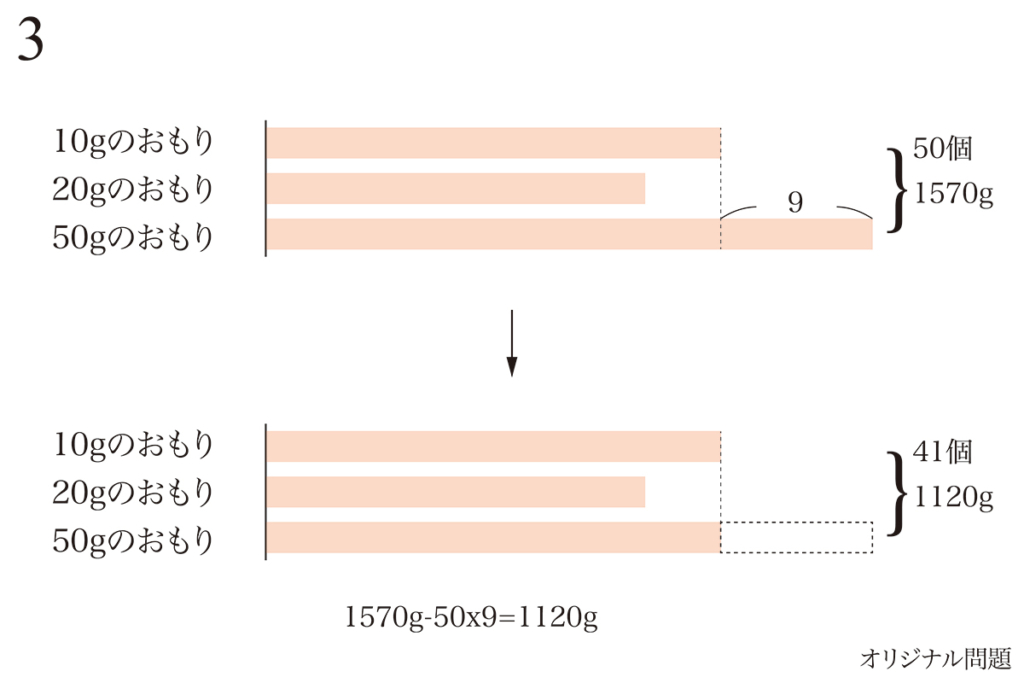
この「おもり」がテーマの問題は、未知数を設定してしっかり立式すれば解けます。

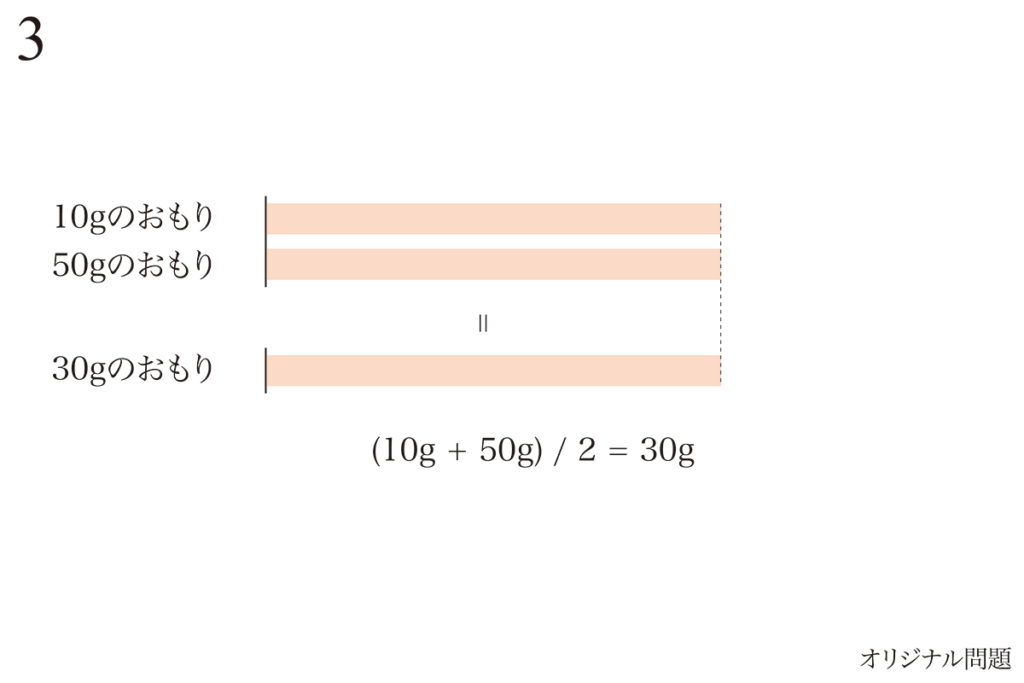
一方で、このような棒グラフが描かれて「平均化」する考え方が表現されていると、

このように採点者・出題者は考えるでしょう。

記述を意識した学び：思考力を深めて学力アップ

上のような表を書いてみるのも良いでしょう。

これらの「グラフを描くか、表を描くか」は問題にもより、考え方にもよります。

受験期後半は志望校が「記述問題を出題しない」場合でも、記述を意識した学びをお勧めします。

それは、「突然、記述問題が出題されても対応できる」からです。

そして、大きな効果は「記述式を意識することで、理解が深まる」からです。

書いてみると色々な発見があり、「思考の軸」が少しずつつくられてゆきます。

すると、問題を解く力も上昇するでしょう。

矢印やメモ書きで簡単に表現：「考えていること」を明確化

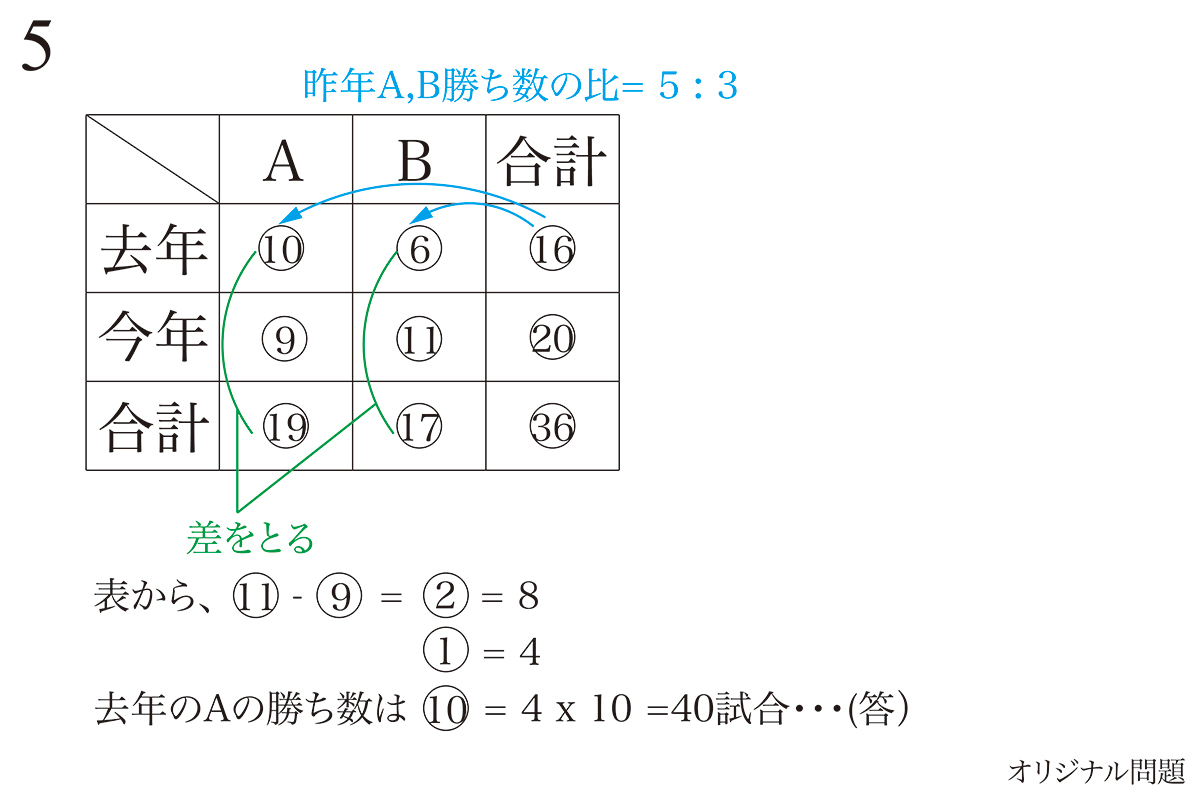
「記述式」と言っても、たくさんの言葉を書く必要はないです。

大学受験の数学ならば、ある程度の論理性やしっかりした文章が望まれます。

中学受験では、メモでも走り書きでも良いので、書くようにしましょう。

上のグラフでは「なぜこのような立式をしているのか」を矢印や「差をとる」とメモ書きで示しています。

記述式の場合、これを書かなくても、

このように採点者は答案を読んでくれます。

それでも良いですが、これらのメモや矢印が書いてあると、

このように高く評価して、良い点数を与えるでしょう。

「簡潔に、端的に」を意識して、自分の思考の流れを表現してみましょう。

これまで、あまり「記述式」を意識してなかった方は少し困るかもしれません。

戸惑う方もいらっしゃるかもしれませんが、まずは書いてみましょう。

これまで、記述式に対する姿勢をご紹介してきましたが、「難しく考えない」ことが大事です。

算数・理科の場合は、ある程度は「良い答案」というのは存在します。

最初は、その「一つの模範解答」を丸ごと書き写してみましょう。

目で追っているだけよりも、書くことは遥かに大事なことで、学びになります。

その際に、出来るだけ「考えながら」書き写しましょう。

色々と自分なりに考えてみると理解が深まり、学力がアップします。

そのプロセスで「記述式への慣れ」が出来てきて、「書き方のコツ」が分かってきます。

「相似形」と「面積比」に着目した解法をご紹介しました。（上記リンク）

「〜と〜は相似形」とか「〜と〜の面積比」など簡単なメモ書きで良いです。

簡単で良いので、「思考の流れ」を書いてみましょう。

メモは「単語をちょっと書く」くらいなイメージです。

それによって、算数の考え方をより深く学べ、多角的に眺める視点が高まります。

そして、記述式への対応にもつながるでしょう。

ただ、式の羅列ではなく「端的に表現」することで算数の思考は磨かれます。

次回は下記リンクです。