前回は「思い切って進んでゆこう〜ポジティブな気持ちで当日まで走ろう〜」でした。
算数の入試問題：様々な工夫
各学校の算数の過去問は、実に様々です。
各科目において、各校の先生方が一生懸命作成している入試問題。
入試問題作成の内情は不明ですが、恐らく、担当者の先生は複数作成しているのでしょう。
来年の入試問題は、
こういう問題が良いのでは・・・
と考えたり、日頃、中学生・高校生相手に授業する中で、
あ、これに関して、
面白い入試問題が作れそうだ・・・
と考えている先生もいらっしゃるでしょう。
「非常に工夫を凝らしている問題」や「少しひねって複雑にしている問題」など様々な入試問題。
中には、大人や大学生が考えても、
これはちょっと
難しい・・・
という問題もあります。
例えば、理科や社会の知識の問題は、その分野に詳しくない限り、大人が見ても、
全然
分からない・・・
ことが沢山あります。
えっ？
そうなの？
大人や大学生は、大学まで
勉強しているから、ある程度知っているんじゃないの？
高校生以降になると、自分の好きな科目に集中する傾向があります。
そして、大学では教養学部（ない場合もあります）を過ぎて、専門課程に入ります。
すると、「専門のこと以外は何もやらない」のが基本になります。
そこで、「専門分野は、非常に出来る」ようになりますが、「それ以外は出来ない」のです。
僕は、理科でバネ・てこ・電気など分野は「ある程度わかる」のですが、生物は全然分かりません。
生物の問題は、見た瞬間に
あ、全然
分からない。
という感じで、「考える気もしない」のが実情です。
このように理科・社会の暗記分野は、「大人・大学生」でも分からないのは、沢山あります。
その中、非常に多岐にわたることを習得・暗記する中学受験生は、大変な苦労と思います。
高校数学は別としても、小学生の算数の基本は、大抵の大人は「分かる」はずです。
でも、「多くの中学入試の問題は、大人にとっても難しい」のです。
なぜなの？
それは、「算数の基本性質」の理解だけでは、解けない問題が多数あるからです。
さらに、中学受験が過熱化した1970年代以降50年経過し、沢山の問題が出題されました。
その中、様々な出題者の先生方は、
誰も見たことがない
問題を作ろう・・・
と考えて、「新たな状況を設定して考える」問題を作ったり、
類似問題はあるが、
ここを少し捻って、特徴出そう・・・
と考えて、先生方の「力作」を出題してきます。
それを「解く」中学受験生は、それら「様々な工夫」に対する力をつける必要があります。
過去問の取り組み方：得点力を高める
受験する学校によりますが、算数は大問3~5題の問題を40~60分で解くことが多いです。
難易度や問題の分量によりますが、問題文を読んで、
あの解き方で、
いけるかな？
と、「パッと取りかかれるか、どうか」で、大きな影響が出るでしょう。
出題形式によりますが、「最初に小問が沢山出る」形式の場合。
この場合は、恐らく、多くの受験生が、
あっ！
あれだ！
と「手が動く」ことが想定されて出題されているでしょう。
そのような小問は、「答えだけ」の場合が多く、計算力なども問われます。
考え方が合っていても、計算ミスしたらX（バツ）なので、
そう・・・
計算ミスしないのは大事だよ・・・
日頃から、ある程度の小問・計算はやっておく必要があります。
そして、大抵の場合にある「様々工夫された大問」は、とても差がつく部分です。
算数の「合格者平均と全体平均の大きな違い」は、大問から生まれています。
「大問ばかり」の場合、難易度によりますが、「合否を分ける問題」があります。
大問は文章が長くて、
状況を理解するのが一苦労・・・
時々、問題文が非常に長い問題が算数・理科で見受けられます。
算数・理科の「思考力を問う」には、「問題文はシンプル」で「考える時間を多く」が理想です。
一方で、問題文が非常に長い問題は、
状況をしっかり
理解する学力をみたい・・・
という意図が出題者にあるのかもしれません。
状況をしっかり・明確に理解する姿勢
大抵は「食塩水が二つ」の食塩水・てんびん算の問題。
「食塩水が三つ」になると、途端に難しく感じられる場合があります。
てんびん算の原理としては、食塩水が三つでも四つでも五つでも「同じ」です。
ところが、「考える対象が増える」と混乱してしまいがちです。
食塩水とかが、
沢山あるのは苦手かも・・・
こういう「状況が複雑な問題」は、自分で「状況を絵に描く」ことをしましょう。
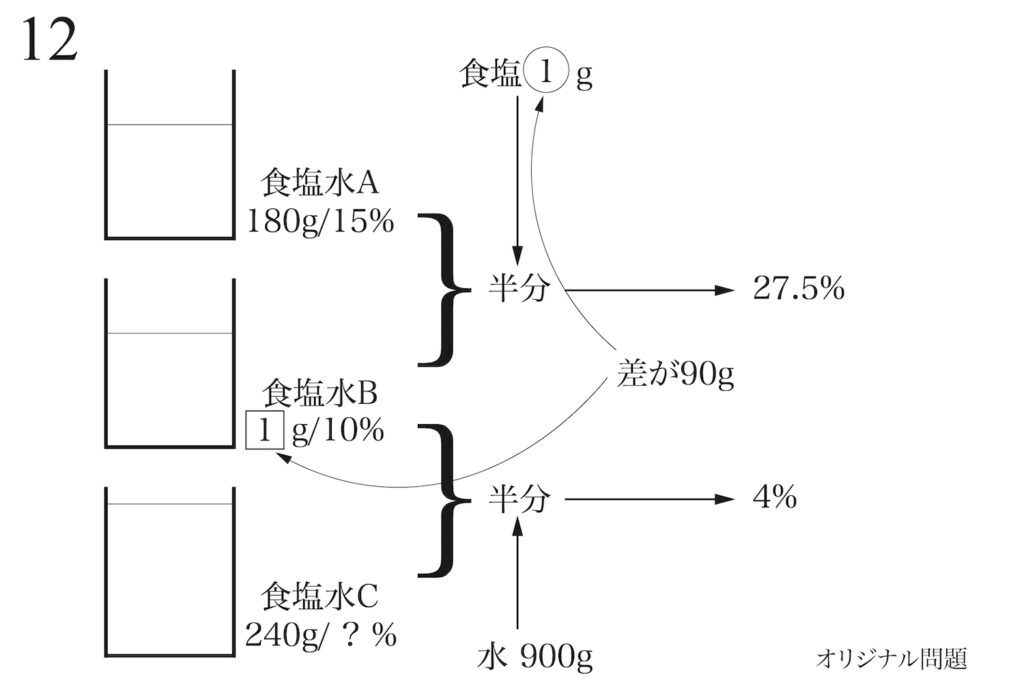
上記のように、「文章で描かれた複雑な状況」を「簡単な絵に描く」と、
随分
わかりやすいね！
これなら、
出来そう！
と、「見かけが複雑」でも、状況を絵に描けば、分かりやすくなります。
そして、「多くの問題を解くよりも、志望校の過去問を習得して身につけること」が非常に大事です。
過去問は早めに取り組んで、「志望校の出題者が何を求めているのか」を理解しましょう。
・状況を「簡単な絵に描く」ことで、理解する
・「絵を描く」時間はかかりますが、「描くプロセス」で解き方・ポイントが見えてくる
・志望校の過去問を習得して、身につける
・過去問は早めに取り組んで、「志望校の出題者が何を求めているのか」を理
瞬発力を鍛える姿勢
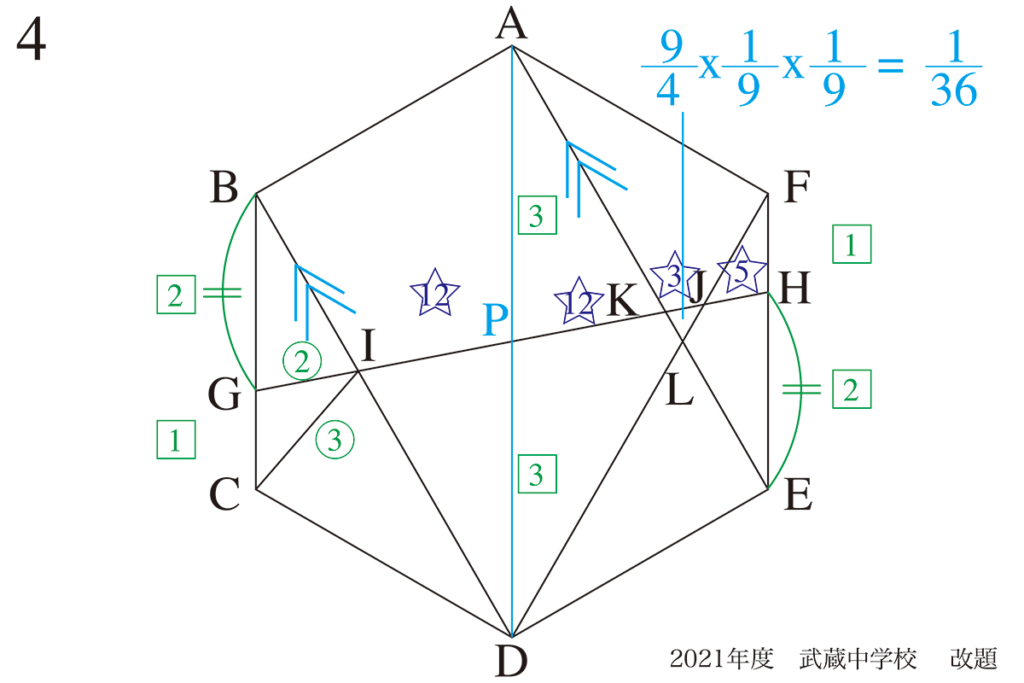
難しい問題をじっくり取り組むことが、難関校〜最難関校受験生は大事です。
そして、算数は「解いたことのない問題」に対して、「パッと」取り掛かる力も大事です。
1題でも良いですから、出来るだけ毎日「初見の問題」を解きましょう。
今まで「やったことのない問題」です。
塾の教材やお持ちの問題集等で、こういう問題があれば良いでしょう。
「中学への算数」は問題集として最高で、おすすめです。
難関校以上の学校を志望する方には、「白百合学園」の算数も良いでしょう。
白百合の算数は、問題文が分かりやすく、適度な難易度の問題が多いのが、とても良いです。
初見の問題をやるときは、「難しすぎない問題」が良いでしょう。
これ以上、参考書・問題集を
増やすのは大変・・・
と思う方もいるかと思いますので、一つの参考としてください。
このような「新しい問題を解くため」に新しい参考書を購入するとき、大事なことがあります。
それは、「1題でも取り組めれば良い」と考えることです。
この問題集は
全部やろう！
と思うと、大変すぎて、テンションが上がらないことがあります。
大事なこと・勉強目的は、
一題一題しっかり
学んで、学力を上げる！
ことで、「問題集をやる」ことは「手段の一つ」です。
このように、算数は総合力・瞬発力を日々鍛える学び方により、成績が上がるでしょう。
