前回は「てんびん算のコツ・食塩水の問題・解き方 3〜難しいことは分ける・比と濃度と量・状況や現象に対する直感・「なぜ？」とバランス・「混ぜる」を描いて理解・仮定して考える〜」の話でした。
食塩水が3つ以上の「てんびん算」
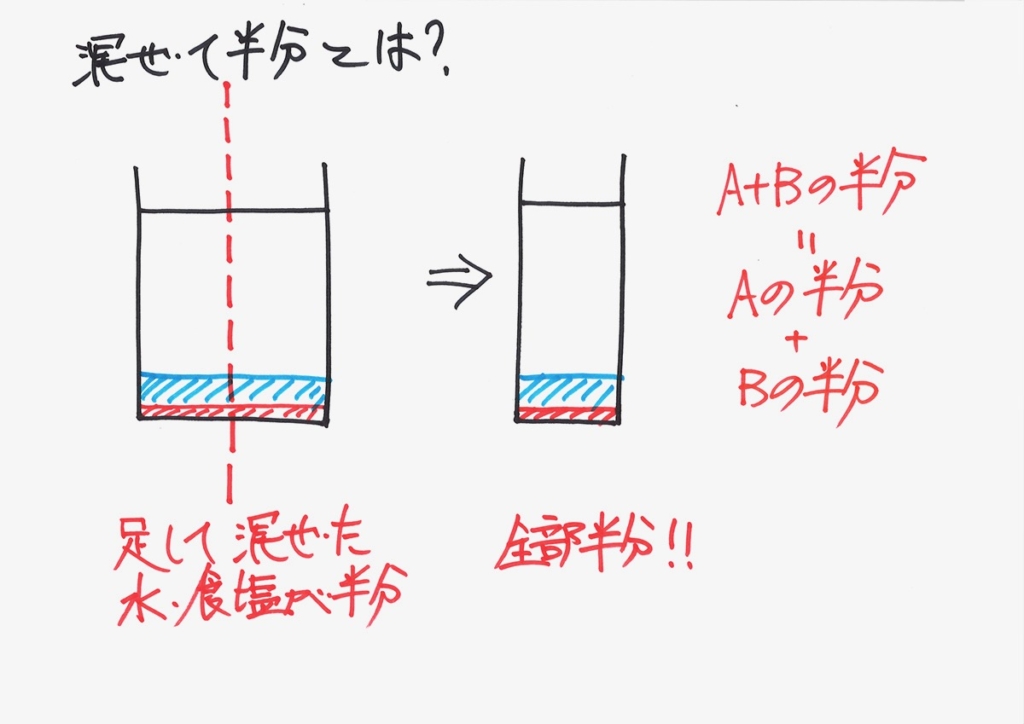
この問題の最も本質で大事なところである、「混ぜて半分」が理解できました。
この問題の良いところは、「算数と理科の両方にまたがる」ことです。
「食塩水を混ぜる」ことは、日常生活では「なかなかしないこと」です。
描いてみれば、イメージがしやすいです。
男子小学生確かに「食塩水を混ぜる」のは
問題だけだね・・・
女子小学生理科実験で
一回だけ、食塩水混ぜたよ！
理科実験でもなければ、日常生活で「何かと何かを混ぜる」ことは少ないです。
ここで、「何かと何かを混ぜる」と「何かが生まれる可能性がある」ので、非常に大事なことです。
これで、てんびんのイメージが出来たので、立式出来そうです。
男子小学生食塩水が3つだと、
難しそう・・・
女子小学生あまりやったことが、
ないけど・・・
てんびん算・てこの原理は、「おもりがいくつになろうと同じ」です。
そこで、食塩水が3つ、あるいはそれ以上の問題があっても、
男子小学生同じように考えれば
良いんだ！
「考える対象が増えても同じ」と考えるようにしましょう。
未知数設置のコツ：計算を簡単に
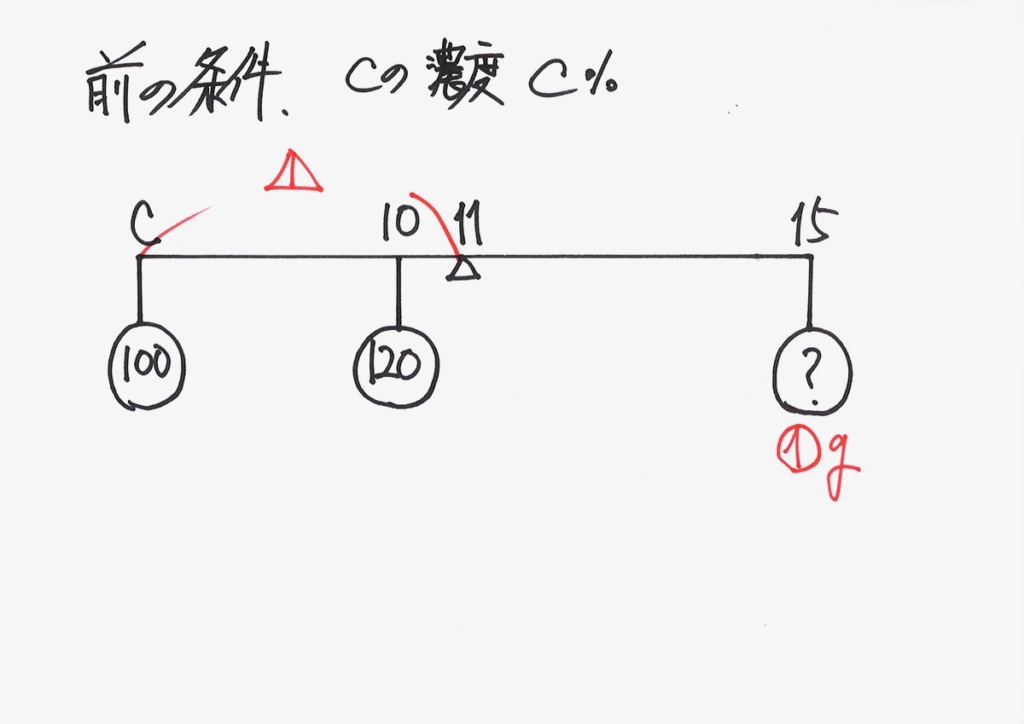
Bの量・Cの濃度を未知数で考えましょう。
ここでは、「Cの濃度と11%の差」を未知数とします。
男子小学生え？なんで？
Cの濃度を未知数にするんじゃないの？
それでも良いですが、「差を未知数」にした方が、「計算が簡単だから」です。
女子小学生「Cの濃度を未知数にする」方が
分かりやすそうだけど・・・
実際に、計算してみましょう。
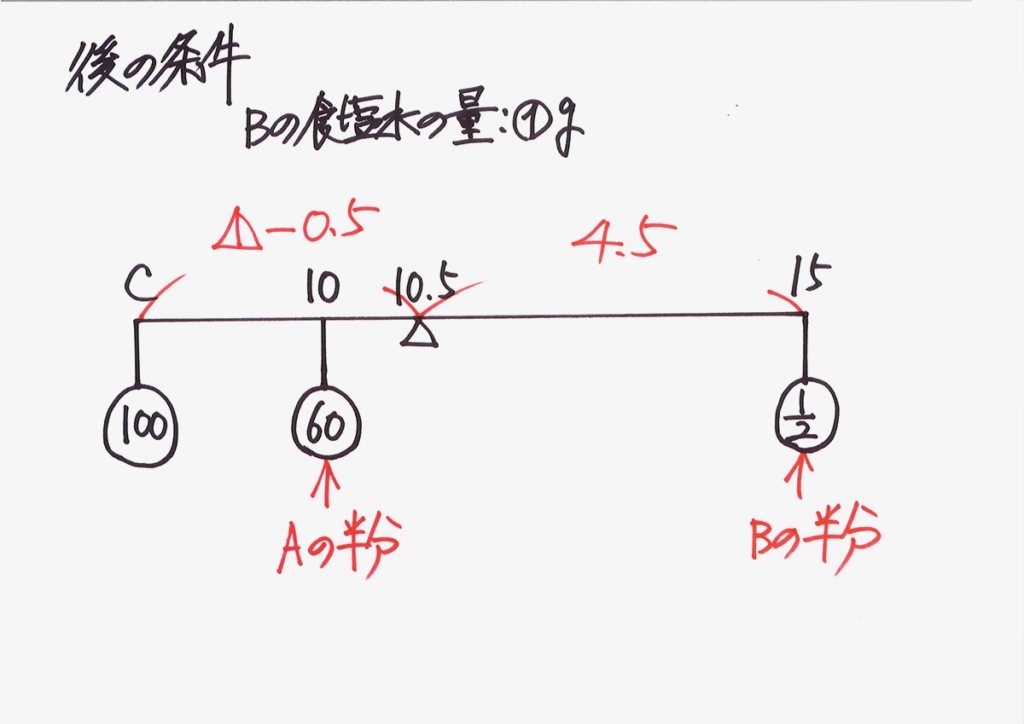
後の条件は、上のようになります。
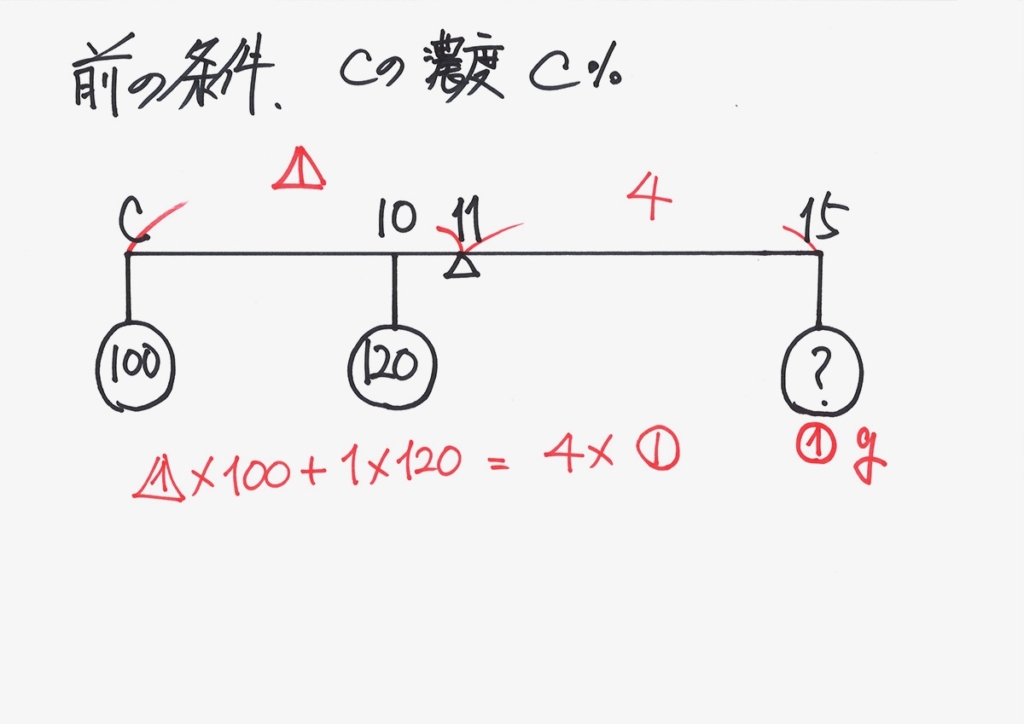
ここからは、バランスとって、立式してゆきましょう。
支点の左側と右側の釣り合いは、「重さx長さ（支点からの距離）」です。
女子小学生確かに、「Cの濃度と11%の差を未知数」の方が、
計算が楽かも・・・
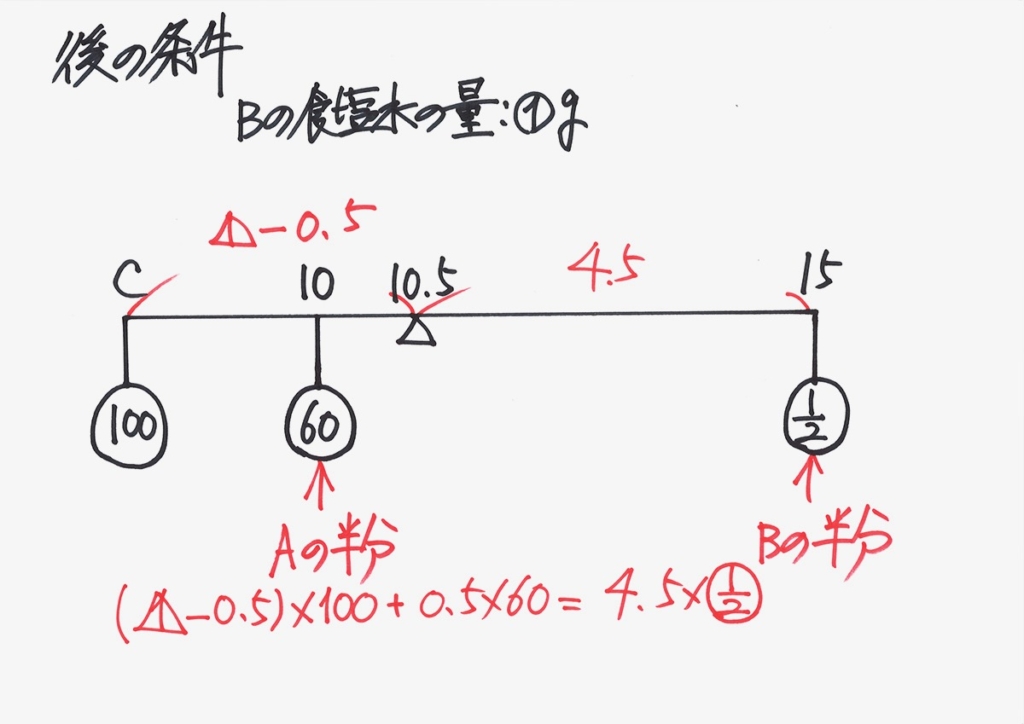
二つの未知数に、二つの（独立した）条件式が出たので、解けます。
計算ミスを防ぐ=「同じもの」を探す
この数式を解くだけですが、こういう時は「同じものがないかな？」と考えましょう。
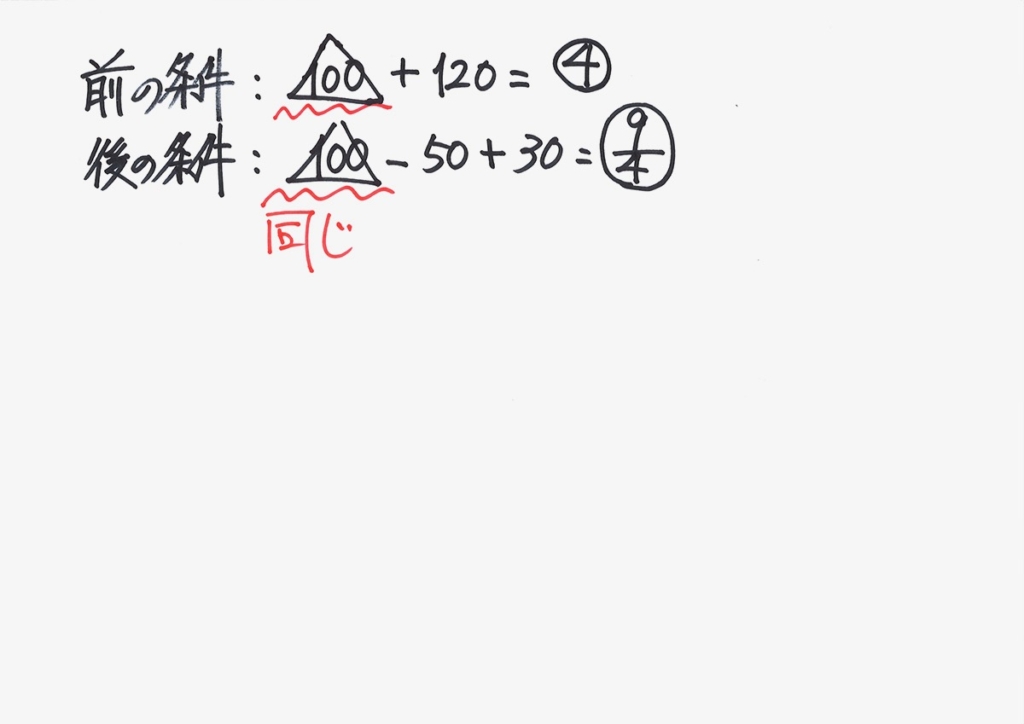
同じものがあると、計算が楽です。
男子小学生「同じもの」が
あったね！
女子小学生同じ量だから、
計算出来そう！
辺々引くと、同じものは消えます。
Bの量・Cの濃度が求まりました。
男子小学生てんびん算って、
便利だね。
女子小学生解いてて、
イメージ出来るから、楽しいかも！
「中学への算数」では、方程式的視点で考えています。
両方の視点で出来るようになると、「多角的視野」が広がるでしょう。
方程式のみで立式すると、計算が複雑になる傾向があります。
試験の時、複雑な計算式を解くと、間違える可能性があります。
出来るだけ「計算が簡単に」なるように考えましょう。
それには、日頃から「多角的視点で考える」ことが大事です。
記事とは異なる、てんびん算の解き方をご紹介しました。
これは、著者の方の考えに対する「異議」ではありません。
「こういう考え方もできるよ」という、一つのご紹介です。
記事が多角的視点を提示しており、様々考えを執筆されている著者の方には敬意を持ちます。
次回は下記リンクです。
