前回は「てんびん算のコツ・難問・解き方 2〜3つの食塩水・描いて気づくこと・食塩水を混ぜる・食塩と水を分離して描く・紙の上で半分に・「頭の中」の世界は自由〜」の話でした。
難しいことは分ける：比と濃度と量
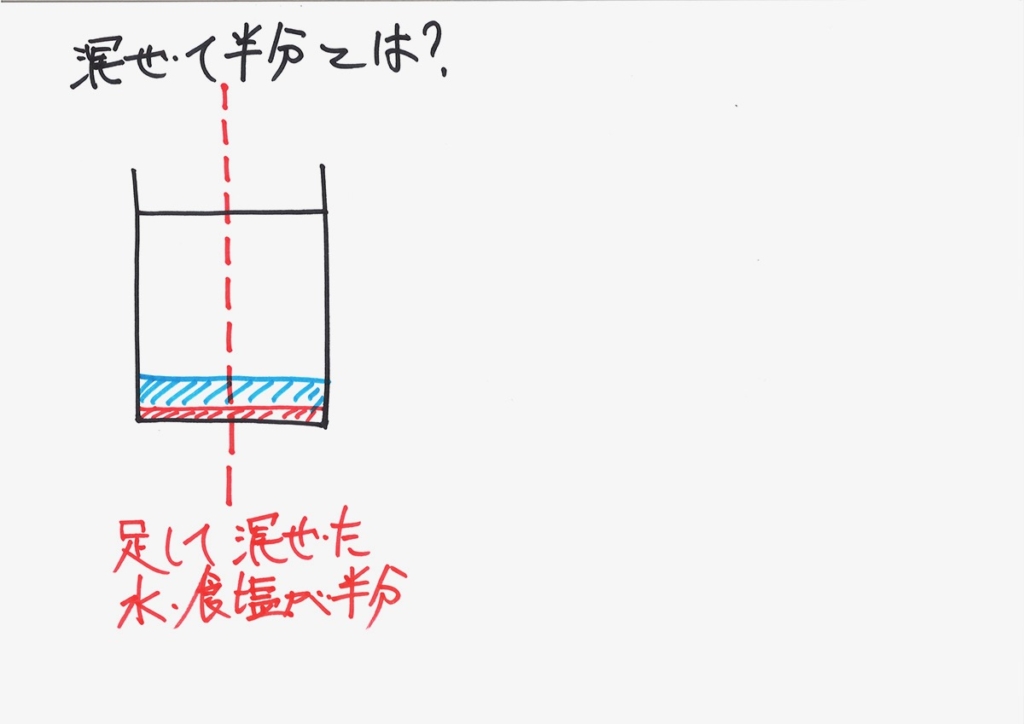
AとBの食塩水を「混ぜて、半分」にすると、濃度も重さも不明になってしまいます。
こういう「分からない」時は、「分割して考える」と良いでしょう。
方程式で立式すれば、こういう複雑な現象は「数値化して、粛々と解く」ことが可能です。
一方で、しっかりと状況を判断・理解する姿勢は、算数では特に大事です。
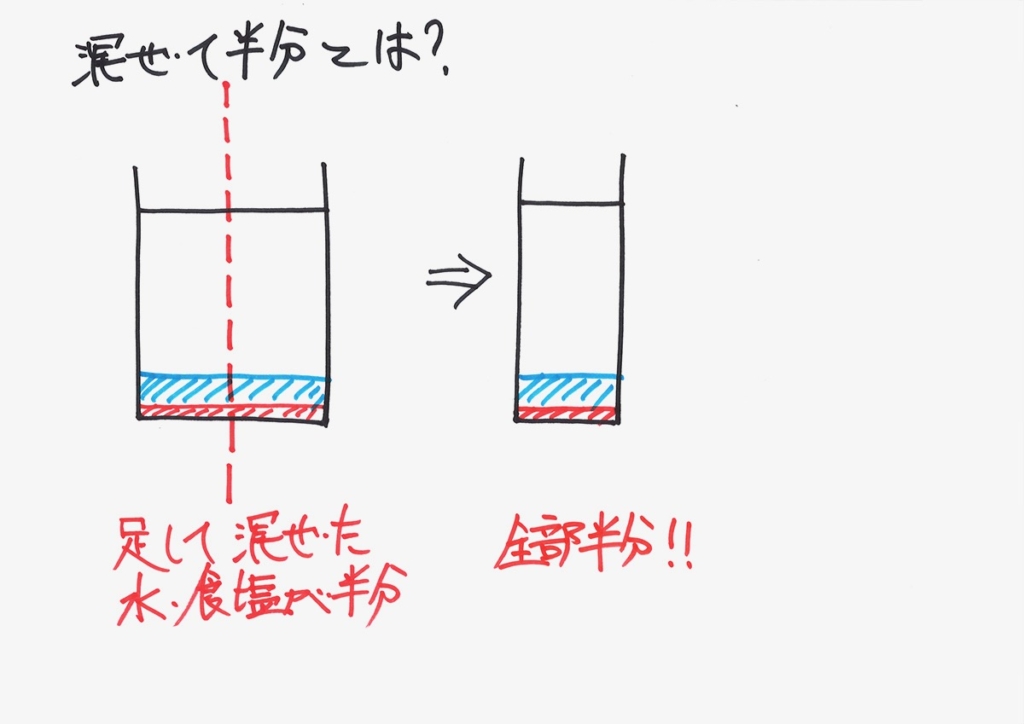
「食塩水を混ぜる」に対して、「水と食塩をそれぞれ分割して」考えました。
すると、「混ぜて半分」なので、文字通り「食塩も水も半分」になります。
男子小学生ということは、
ひょっとして・・・
男子小学生分かったよ！
「A+Bの半分」の正体が！
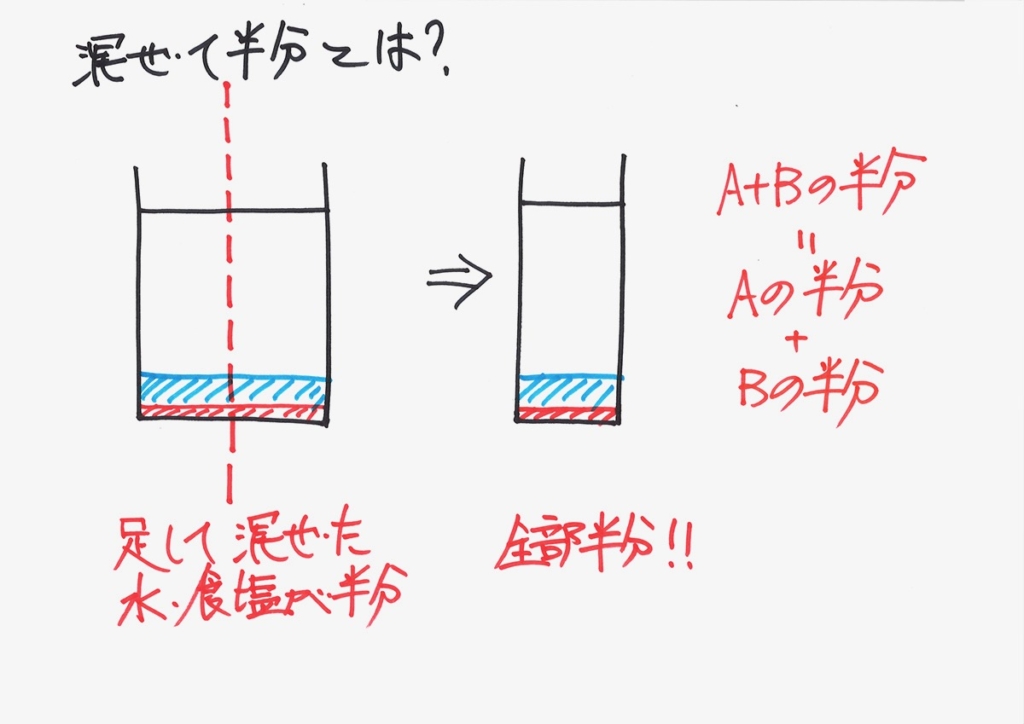
女子小学生「A+Bの半分」は
「Aの半分+Bの半分」だね！
女子小学生これは
面白いかも！
こうして「あっ、分かった！」という時は、とても嬉しいです。
「分かる楽しさ」を楽しみながら、学びを進めてゆくと良いです。
「A+Bの半分」は「Aの半分+Bの半分」です。
これで、状況が把握できました。
「混ぜる」を描いて理解：仮定して考える
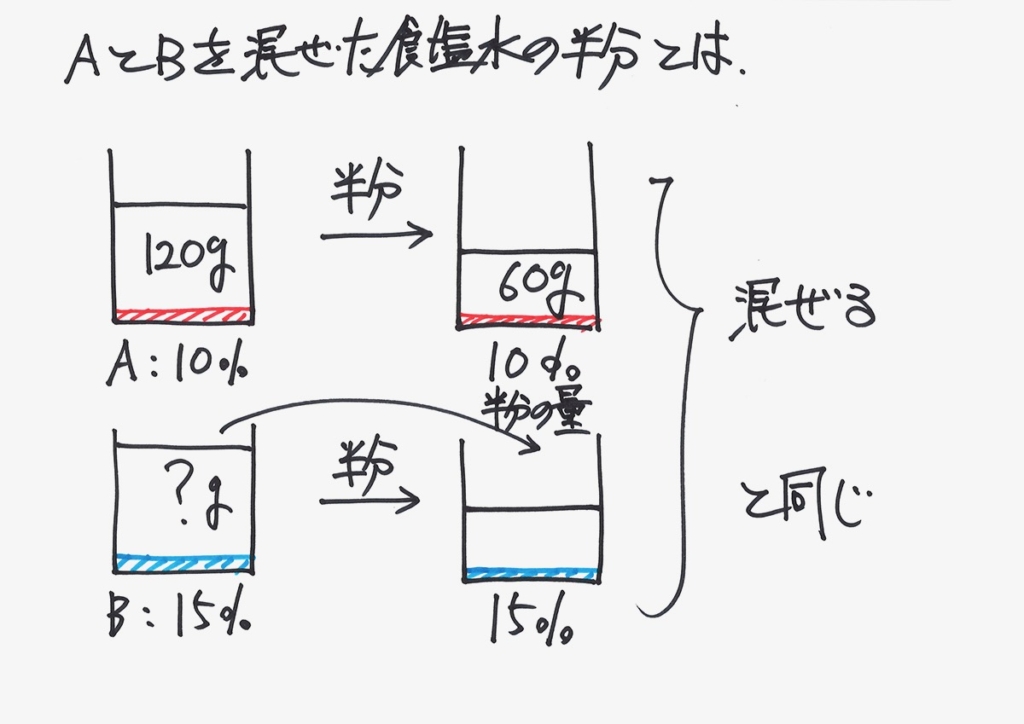
後の条件で「混ぜて半分」は「半分にして混ぜる」であることを考えましょう。
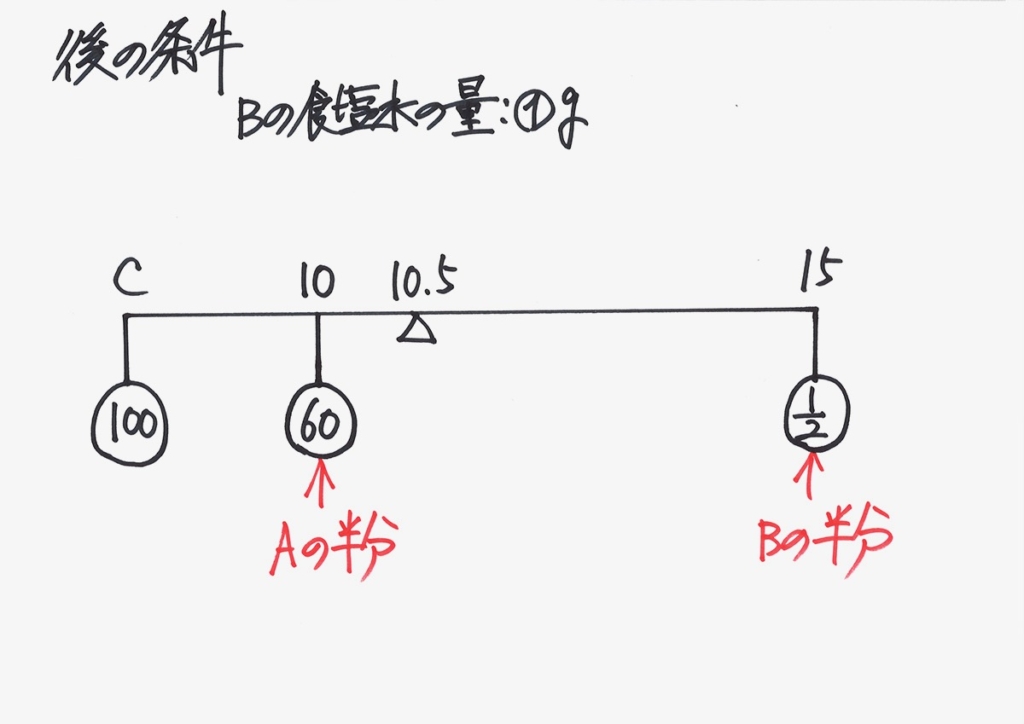
女子小学生これなら、
バランスが考えられね！
男子小学生少し
解けそうな感じになったね！
男子小学生でも、ちょっと待って・・・
Cの濃度は、分からないんだよね・・・
女子小学生濃度によっては、つり合いのどちらになるか、
分からない・・・
釣り合いの、右か左かでバランスが変わります。
Cの濃度が「てんびんの右の方だったら、どうなるか」を考えてみましょう。
2つの条件を、もう一度まとめて描いてみましょう。
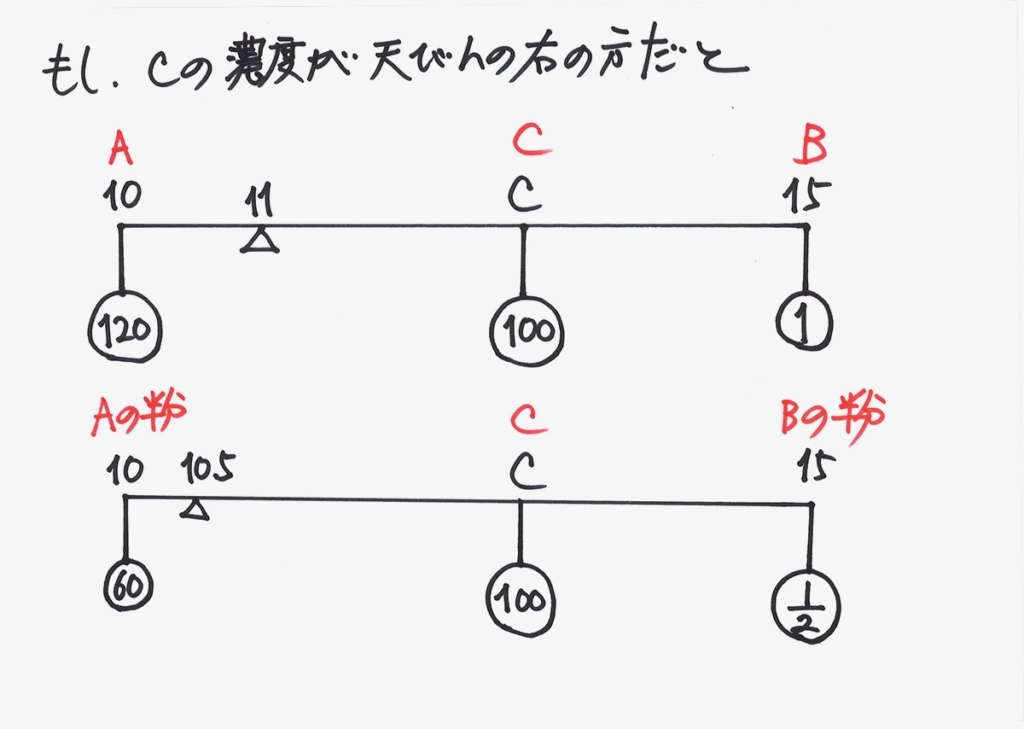
男子小学生あれ？
これつり合うかな？
女子小学生なんだか、
右の方が、大きそう・・・
状況や現象に対する直感：「なぜ？」とバランス
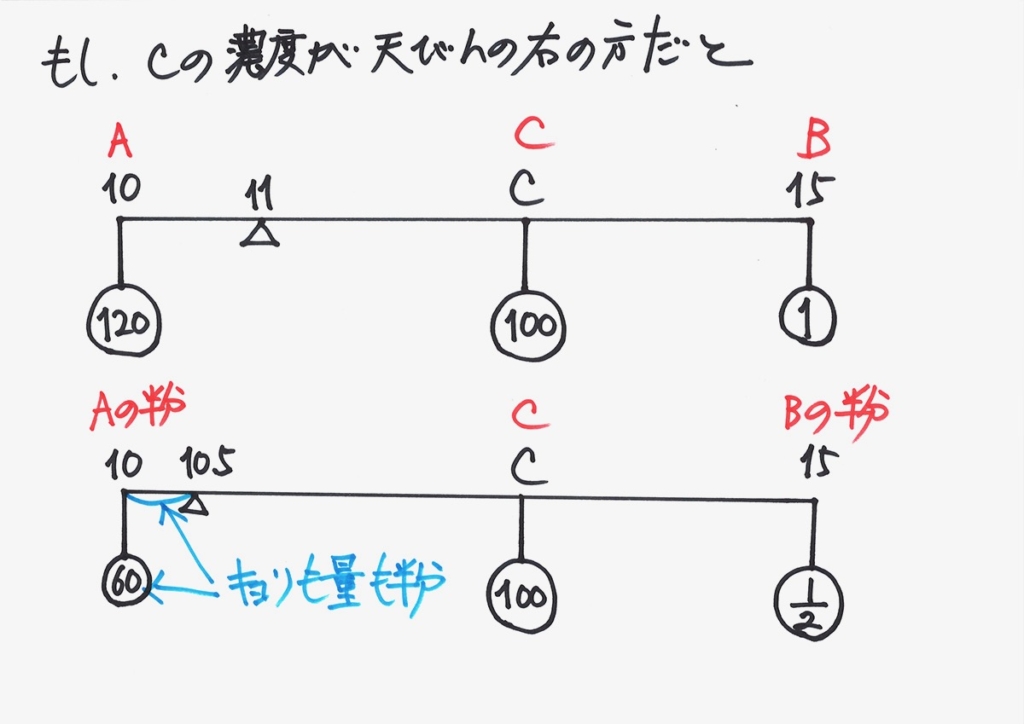
「てんびん」のつり合いは、「重さx長さ（支点からの距離）」です。
二つの条件で、左側のAは「重さも長さ（支点からの距離）も半分」です。
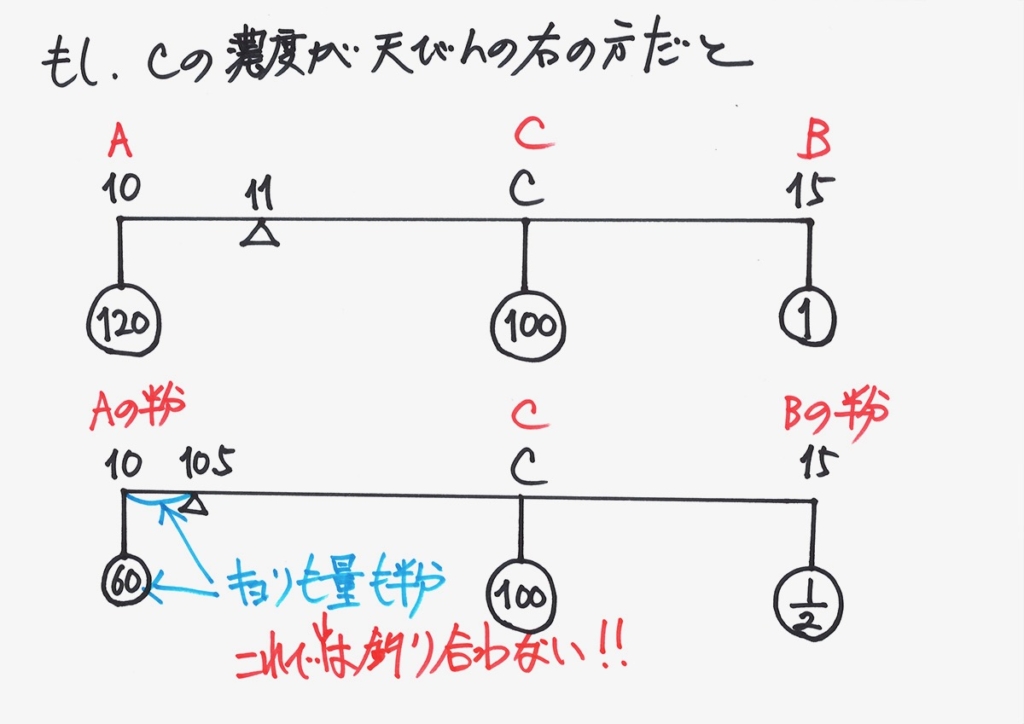
男子小学生これでは、視点の右側の
「回転する力」が大きいね！
女子小学生これは
つり合うのが難しそう・・・
この状況では、「つり合うことは出来ない」と直感で分かります。
そこで、Cの濃度は「てんびんの左の方」になります。
「つり合わない」は、「感覚的に分かる」ことが大事です。。
このように、「状況・現象に対する直感」を大事にすると算数や理科は理解力が深まるでしょう。
算数や理科の「てんびん」は「つり合う」ことが多いですが、
内野吉貴「なぜつり合うのかな？」と
バランスを考えると良いです。
もし「ちゃんと計算して考えたい」方は、計算してみましょう。
計算してみると、おかしなこと（矛盾）になります。
余力のある方は、トライしてみましょう。
これで、てんびんが作れました。
男子小学生ここまで
来たら、出来そう！
女子小学生あとは
計算すれば良さそうだね！
バランスを考えて、解いてみましょう。
次回は下記リンクです。
