前回は「てんびん算と食塩水の問題〜「なぜ？」と考え方・上皿てんびんのイメージ・「てんびん=バランスを取る」こと〜」の話でした。
実社会と「てんびん算」：「なぜ？」の理解
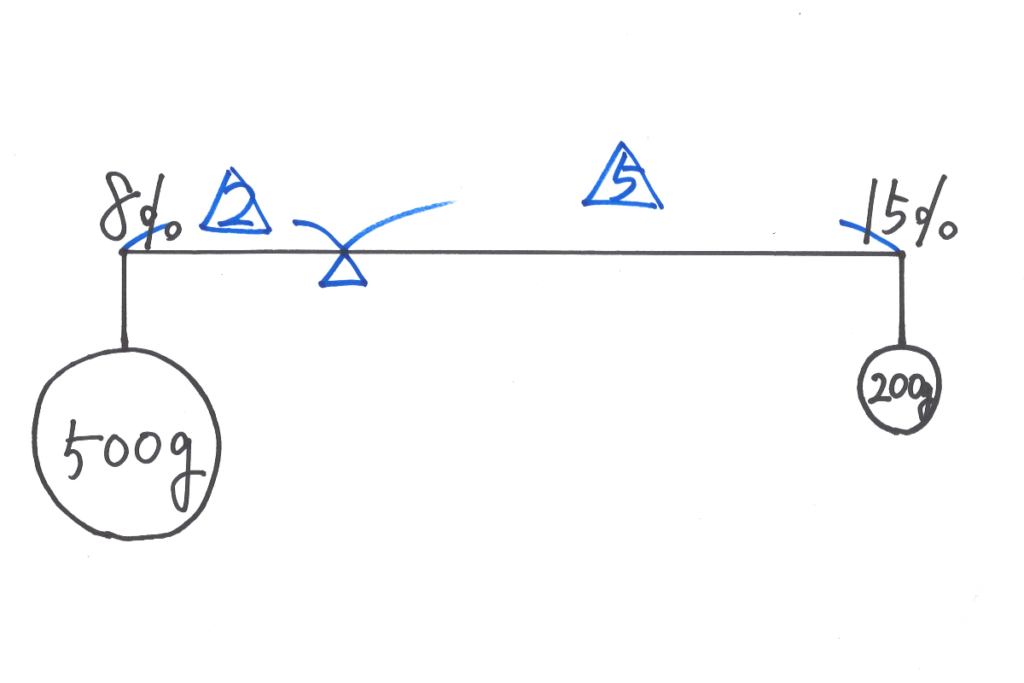
「バランスを取る」という本質的な考え方の「てんびん算」。
このコンセプトは、実社会でも大変有効です。
例えば、株式投資をしていて、ある株を100円で300株購入したとします。
その後、同株が急落し79円になったとします。
この場合、20%以上の含み損を抱え、頭を抱えてしまいます。
日本人Pこれは
弱ったな・・・
株式投資をしている方なら、誰しも経験することです。
株価はまた戻るかもしれませんし、さらに上昇するかもしれません。
場合によっては、下落した時はチャンスです。
日本人Pチャンスなのか・・・
それとも、さらに下落するのか・・・
日本人P・・・・・
少し考えてみて、
日本人Pこれは
チャンスだ！
「チャンス」と判断したとします。
どのくらいの株を購入して、購入金額を下げるのが良いでしょうか。
・本質的には「混ぜること」=「バランスをとること」
・両側が「つり合う」イメージを大事に
この時、てんびん算のコンセプトが生きます。
ここでは、思い切って400株購入して、取得株価を下げましょう。
食塩水の時と同様に、今回は株価を濃度と同じように考えて、株数を水量と考えます。
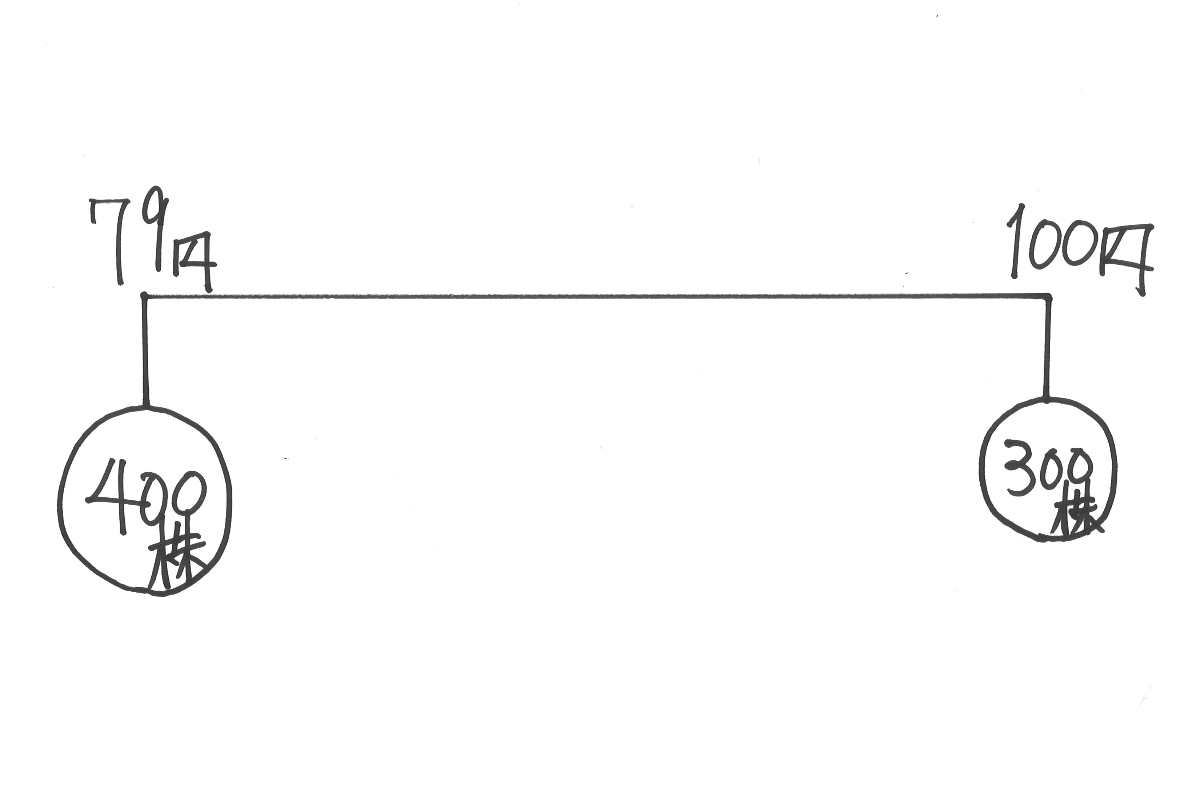
100円の時の300株より多いので、「79円と100円の中央の89.5円」よりは下がりそうです。
食塩水の時と同じように、株数でバランスが取られ、釣り合います。
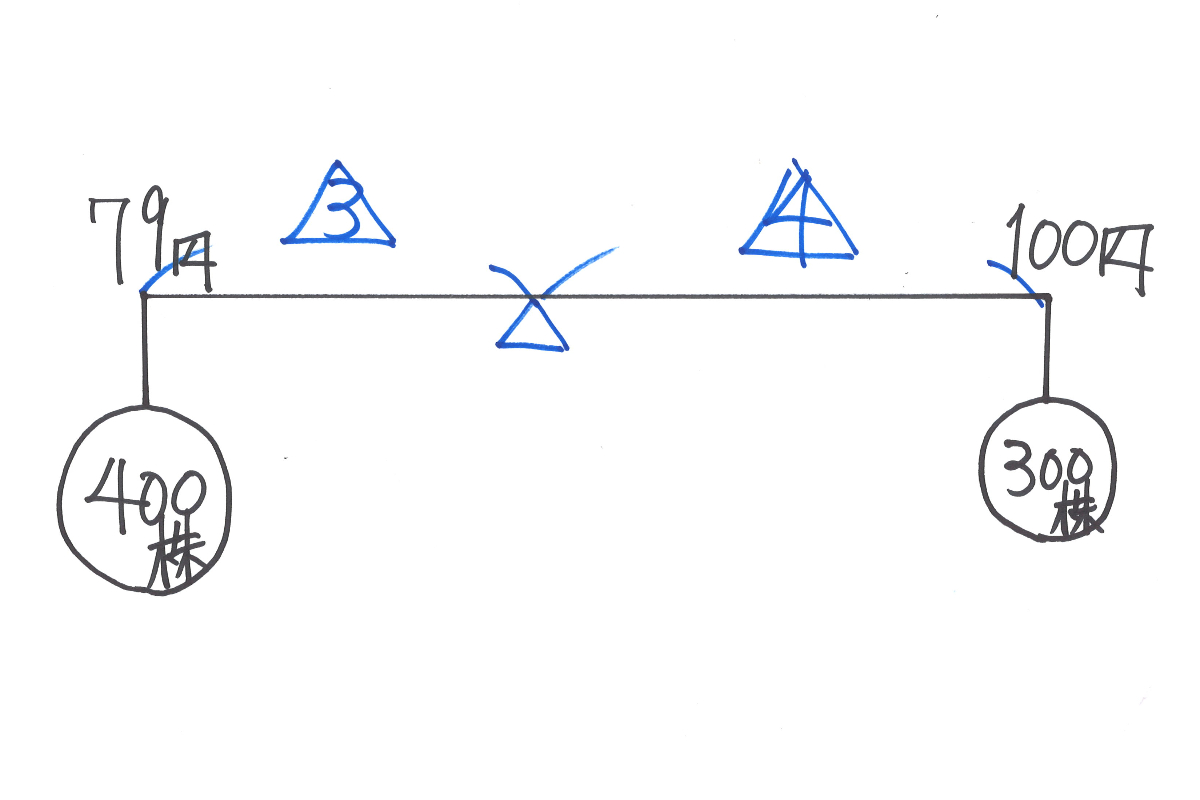
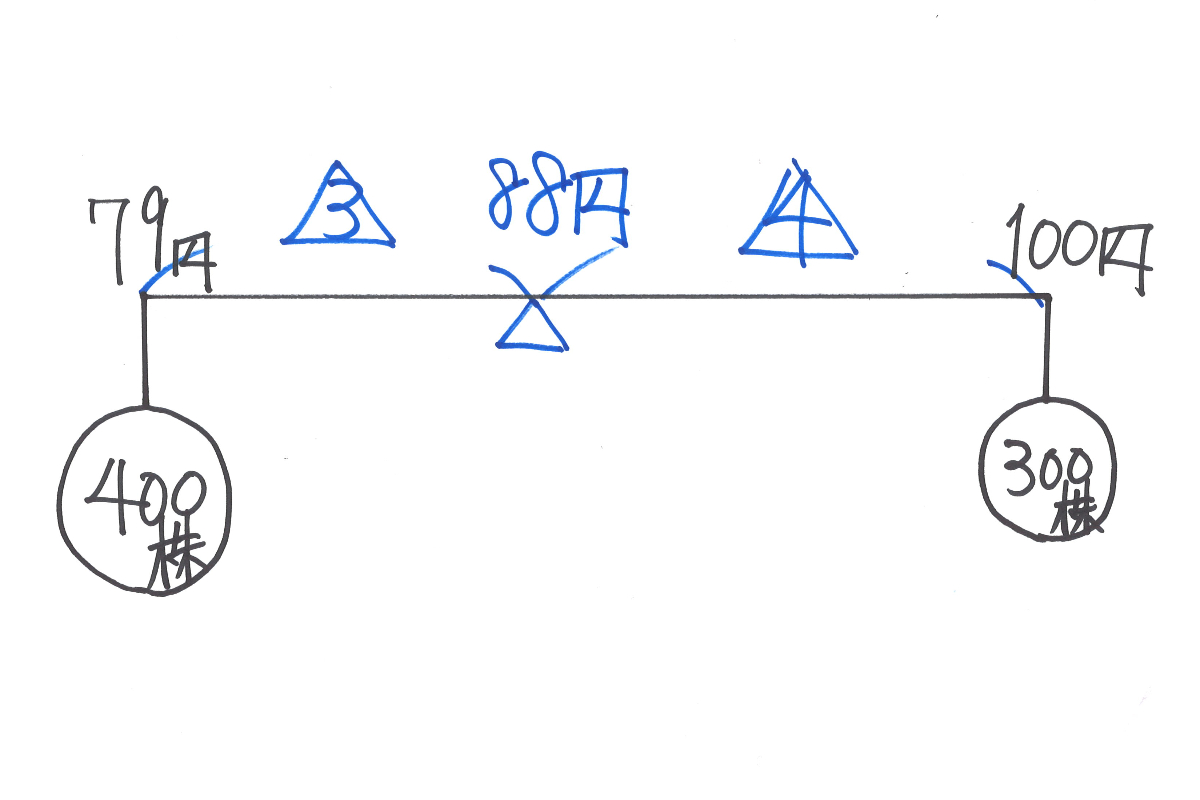
ここで、100-79=21円を「3:4」に按分します。
すると、21/7=3円となり、釣り合いの株価は、
79+3×3=88円と計算できます。
「算数的コンセプト」と実生活
実際の株式投資の際には、これほど綺麗な数字にならないことが多いです。
中学受験の算数では、「食塩水の濃度と量が想定」された上で問題が作成されています。
そのため、食塩水の濃度は大抵は整数か小数点一位くらいの、比較的綺麗な数字になります。
「3つの食塩水とてんびん算」に関する話を、上記リンクでご紹介しています。
大まかな数字を頭に描くことは、時間も掛からず大変有効です。
株式投資に限らず、取引先との交渉等色々な実社会で、このコンセプトは役立ちます。
実生活において、高校生の時に習う微分積分を使用することは、ほとんどありません。
数学者・サイエンティスト以外の一般的な方は、
日本人P社会人になって
微分積分は一切使わない・・・
日本人P微分積分は、
大学2年くらいまでかな・・・
「微分積分は使わない」や「微分積分は実社会と無関係」という方も多いでしょう。
一方で、こういうコンセプトを理解しておくと、実生活の幅が広がるでしょう。
このように「基本的な算数の考え方」は、知っておくと重宝します。
子どもと一緒に親も学ぶ機会：子どもと接する貴重な時
「本質的なコンセプト」を頭で考えながら仕事したり、生活してみるのも面白いです。
子どもが中学校受験の勉強をしている時は、一緒に勉強したり考える方もいるでしょう。
男子小学生この問題分からないんだけど、
パパ、分かる？
受験生の父親う〜んと、
これはね・・・
せっかく学んだ算数を、ただ「受験のため」にするではなく、活用する方法があるかもしれません。
学んだことを様々に展開することは、頭を使うので能力の向上につながります。
そして、なにより楽しいです。
受験生の父親確かに、
こう考えると・・・
受験生の父親こうなって、
こうなるな・・・
「てんびん算のコンセプト」に限らず、色々な考え方を頭で思い描いてみるのも面白いです。
子どもと一緒に、楽しみながら学べると一番良いでしょう。
男子小学生てんびん算が
なんとなく、分かってきた・・・
受験生の父親要するに、
「バランスをとる」ことだね。
子どもパパと一緒に勉強したら、
ちょっと分かった！
子どもが喜んでくれたら、親としても嬉しいことです。
すると、子どもの知的好奇心が大いに刺激されることでしょう。
そして、その「知的好奇心」のアップは、学力アップにもつながると考えます。
次回は下記リンクです。
