てんびん算と食塩水の問題〜「なぜ？」と考え方・上皿てんびんのイメージ・「てんびん=バランスを取る」こと〜｜中学受験・算数

前回は「成績アップと育む好奇心〜身近な「なぜ？」を大事に・大発明家エジソンを生んだ「なぜ？」の気持ち・コップの氷を見て「なぜだろう？」〜」の話でした。

てんびん算の基本：「なぜ？」と考え方

今回は「てんびん算」のご紹介です。

中学受験算数のコンセプトの一つ、「てんびん算」は多くの方がご存知かと思います。

中学受験した人は、

ご存知の方が多いと思います。

小学校高学年の子どもは、

塾などで習っているかもしれません。

中学受験の算数においては、「比」や「図形」など、数学的に本質的な事柄もあります。

図形問題の考え方のポイントを、上記リンクでご紹介しています。

あるいは「てんびん算」や「旅人算」などのように、「解法テクニック」的な考え方もあります。

僕は「テクニック」は、テストにはある程度有効ですが、長期的視点からは弊害もあると考えています。

「コンセプト」や「アイデア」などの言葉で表現したいと思います。

「てんびん算」のコンセプトは、非常に本質的・直感的です。

問題の解法としては、非常に優れていると思います。

てんびん算の具体例：上皿てんびんのイメージ

例えば、食塩水を混ぜる問題で、

上記のような問題があります。

基本的な考え方は、下記になります。

もちろん「正しい」です。

「てんびん算」の考え方は、次のようになります。

まずは、てんびんを描きます。

そして、8%の濃度のところに「500gのおもり」、15%の濃度のところに「200gのおもり」を置きます。

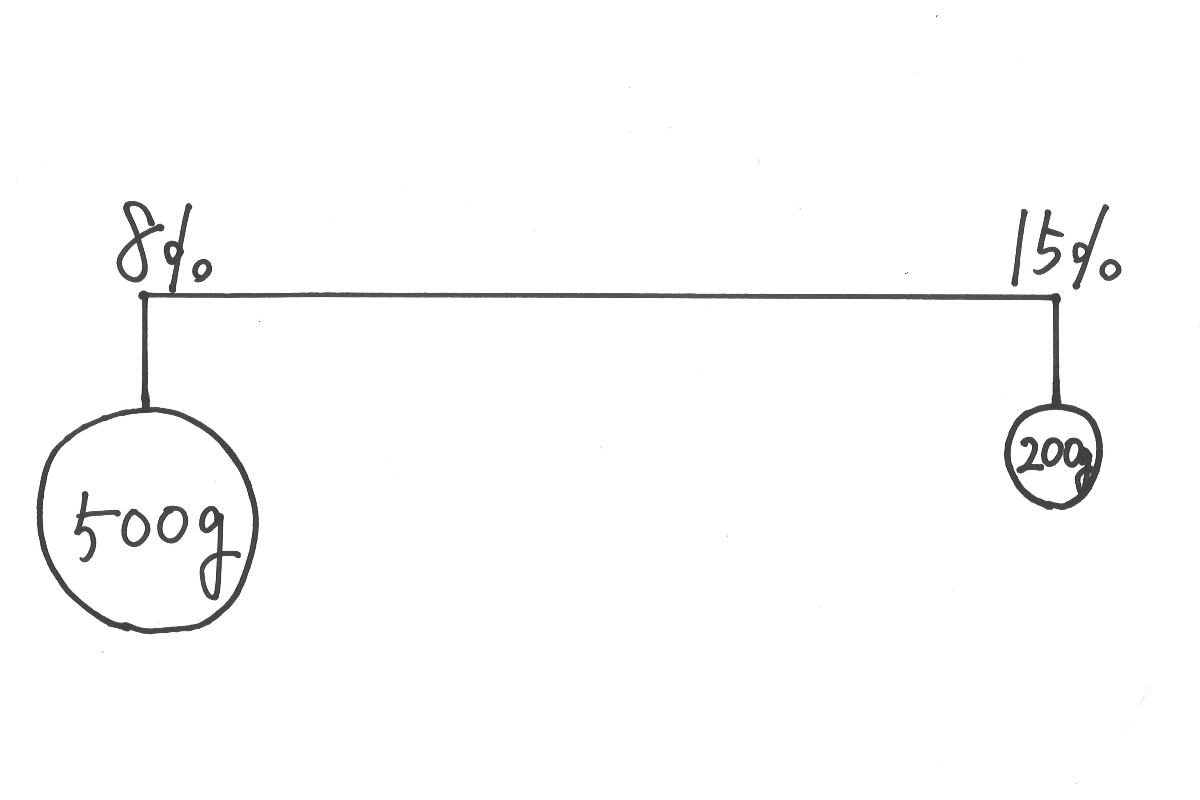
これらの天秤が「どこでつりあうのか」を考えると、

てこの原理（モーメント）で、下記のようになります。

ですから、8%と15%の間の7%を按分して、下記の通り10%になります。

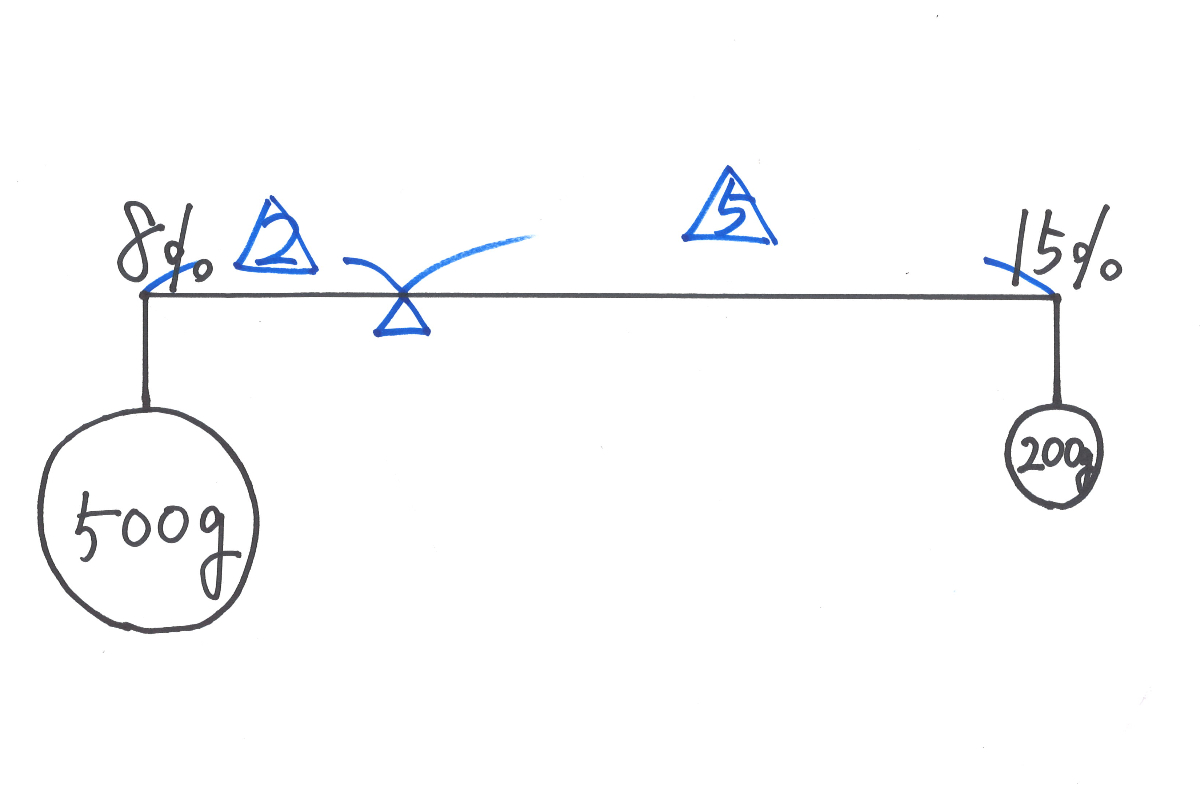
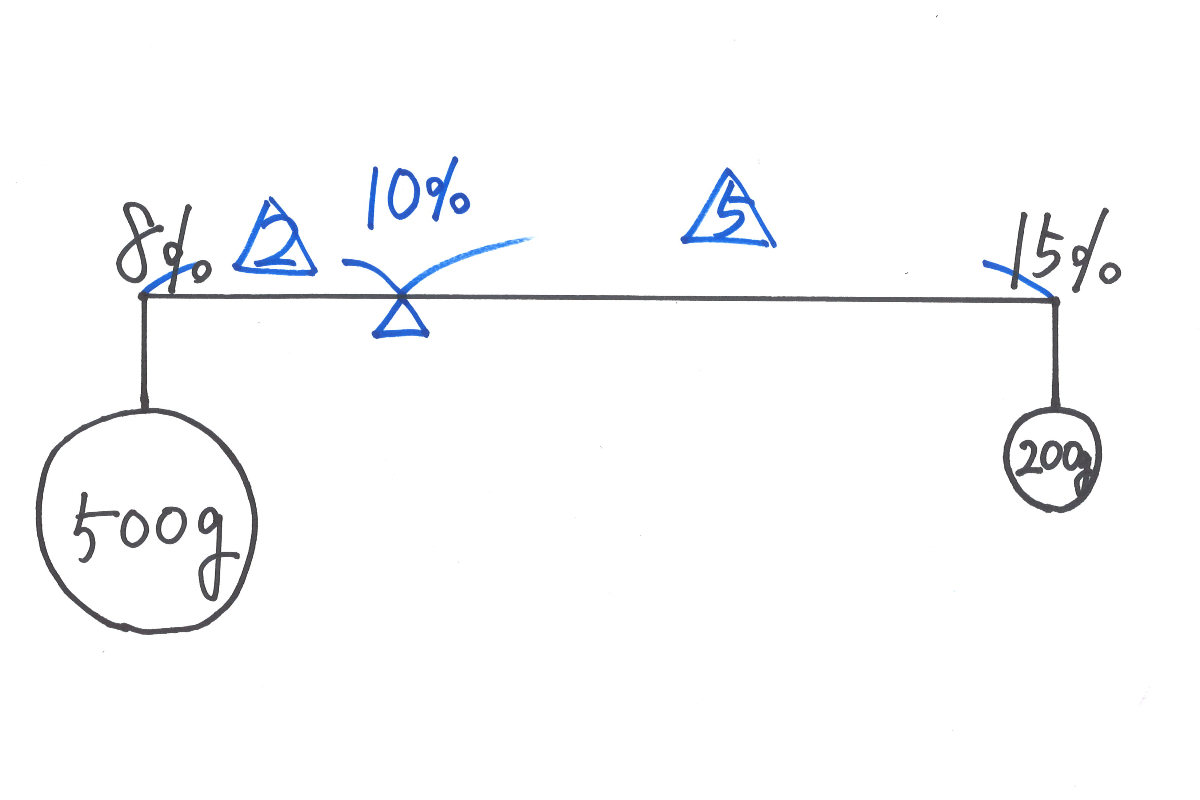
「てんびん=バランスを取る」こと

この考え方は、混ぜる食塩水の数が3つなど多くなっても同じです。

3つの食塩水・てんびん算の話を、上記リンクでご紹介しています。

また、濃度がわからない場合など、非常に効果的に解くことができます。

解法としてわかりやすく、時間も短くできます。

この考え方は「物事のバランスを取る」ことで、非常に本質的です。

実社会で取引をしたり、協議したりする場合でも、「バランスを取る」ことは大事です。

てんびん算で「バランス感覚」養いつつ、問題解決能力も高めみましょう。

てんびん算を単に「解法テクニックの一つ」として学ぶのではなく、そこにある原理を考えてみましょう。

その「面白い」という気持ちが大事です。

その気持ちを大事にして、色々と勉強してみましょう。

次回は下記リンクです。