前回は「方程式ではなく大事な「小学生らしい」柔軟な思考〜中学受験算数と一次方程式・「方程式で解く」とは考えない姿勢〜」の話でした。
中学受験算数と二次方程式
今回は、中学受験算数における「二次方程式の扱い」に関する話です。
①などの二元・三元一次方程式を「方程式」と考えずに、立式して解くのは良い面があります。
未知数を設定して「条件に応じて立式して計算」すれば、大抵の問題は解けます。
途中の計算が少し煩雑になる場合がありますが、
男子小学生この問題は
どうやって解こうかな・・・
女子小学生う〜ん、
全然分からない・・・
「悩んで手が止まる」くらいなら、「未知数を置いてドンドン計算する」方が良い面があります。
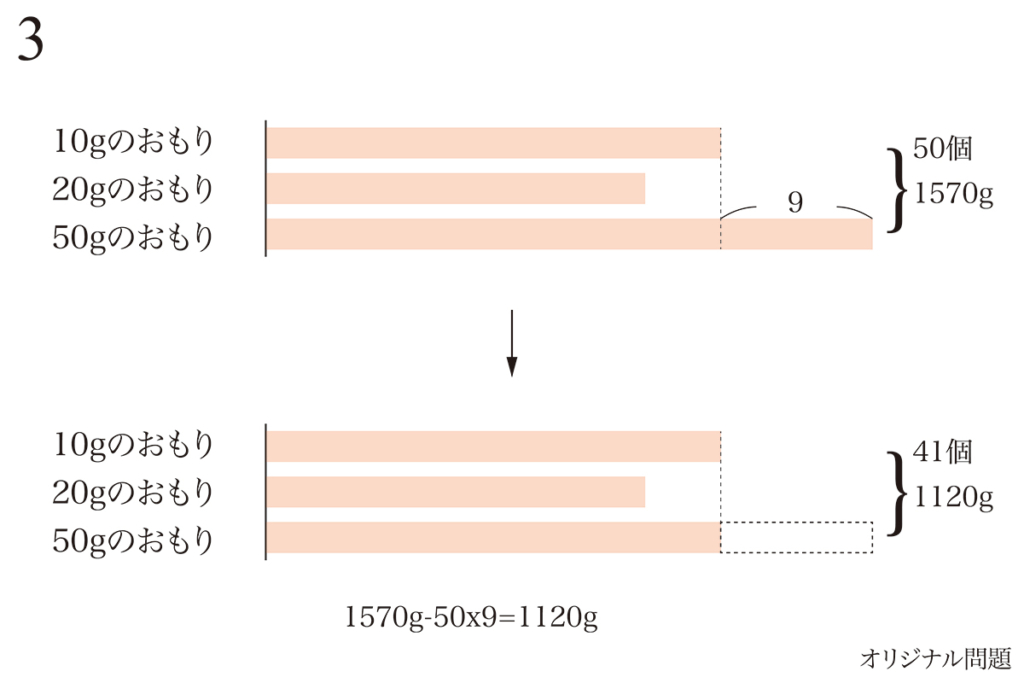
一方で、「闇雲に未知数を設定しない」で、小学生らしい柔軟な思考で算数を学ぶことは大事です。
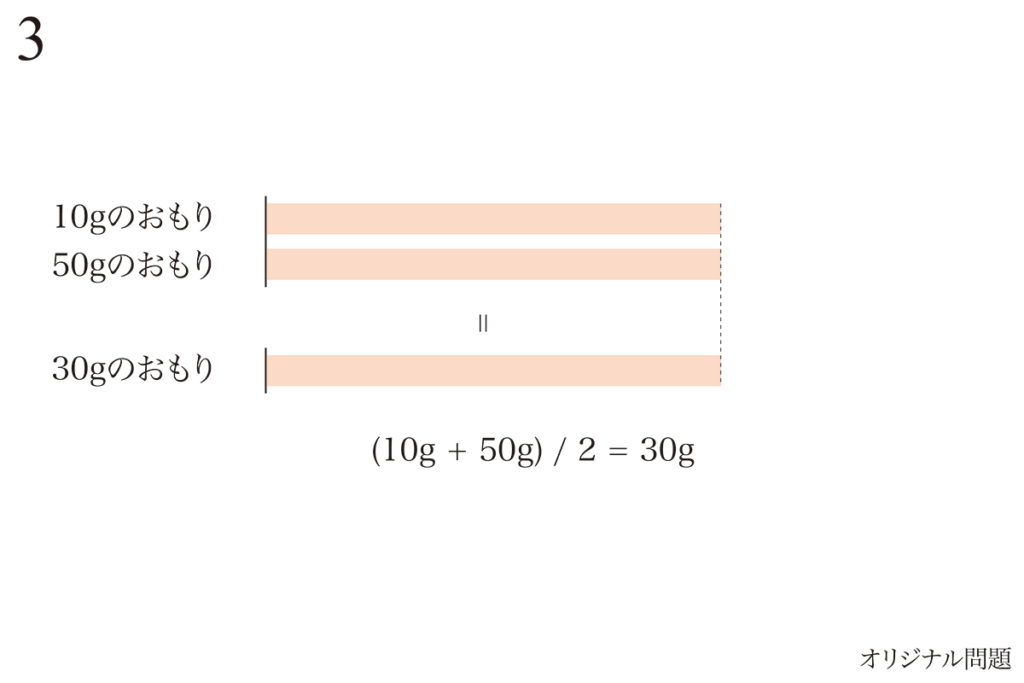
「平均をとる」という考え方は、とても本質的で「算数の発想」としてはオススメです。（上記リンク）
上の例のように、「未知数同士が掛けられていない」方程式を一次方程式と呼びます。
「未知数同士が掛けられる」場合は、二次方程式、三次方程式・・・となり、難易度が急上昇します。
中学受験の小学生は、普通は「一次方程式まで」で、二次方程式は中学生になってからです。
ところが、中学受験生の中には「二次方程式で解く」方もいます。
面積算のような問題において、
女子小学生縦をx、
横をyとおいて・・・
こう計算すると、二元二次方程式となります。
僕が小学生の時は、
男子小学生A俺は二次方程式が
解けるんだ！
このような塾のクラスメートに対して、
小学生の筆者えっ、二次方程式！
すごいなあ・・・
驚いた、というよりも驚愕した経験があります。
それほど、一次方程式と二次方程式では難易度が全然違います。
そもそも「二次方程式」という言葉自体が、小学生にとって「とても難しい」ように感じられます。
二次方程式の発想と算数のセンス：方程式とセンスは無関係
実は、面積算などの問題を二次方程式で計算してみると、
男子小学生Axyが共通だから、
消せる・・・
多くの場合、xyの項が引き算によって容易に消去できます。
すると、
男子小学生Axyがなくなって、xとyだけの
式になった・・・
そのため、実際は二元一次方程式となるので、いつもの「よく考えるやり方」と同一になります。
その意味では「大した差がない」様にも思います。
結果的に「大して変わらない」のですが、それでも「未知数同士を掛ける」のは高度な発想です。
慣れてしまえば、中学受験の問題では「二次の項が現れても、消える」ので、難しくないかもしれません。
女子小学生でも、やっぱり未知数同士掛けるのは、
とても難しい気がする・・・
この「二次方程式の発想」が「難しくない」方は、学んでも良いでしょう。
ところが、大抵の小学生にとっては、
男子小学生やっぱり、
これは難しいよ・・・
「難しい」と感じるでしょう。
その時は、無理をしないで「二次方程式の発想」はやめた方が良いでしょう。
こういう時は、
男子小学生僕って、算数や数学の
才能がないのかな・・・
自信をなくしてしまい、「才能がない」と誤解してしまうかもしれません。
実は、小学生の時に「方程式が出来るかどうか」はセンスと無関係です。
これらの「方程式が理解できる」方は、単に「機械的に立式している」だけの場合が多いのです。
そこで、こういう「方程式の考え方が合わない」方は算数的発想で学び続けましょう。
将来性がある「好ましい」算数的柔軟な発想を持つ大事さ
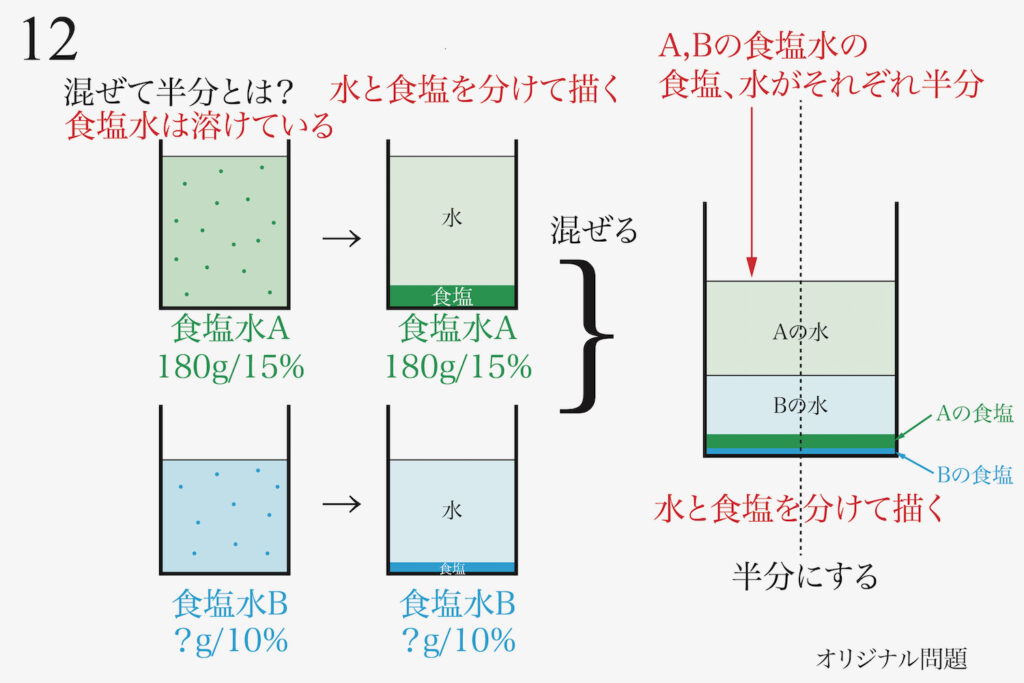
食塩水の問題で、「混ぜて半分」を図を描いて考えました。
ここで「混ぜて半分」は「半分にしてから混ぜる」と同じであることは、本質的です。（上記リンク）
これは算数に限らず、理科的発想でもあります。
こういう発想・考え方はとても良いと思います。
一方で、上の「混ぜて半分」は、未知数を置いて方程式で立式しても解けます。
つまり、図を描いて考えなくても、
男子小学生食塩水の量か、濃度を未知数にして、
混ぜることを立式して・・・
ひたすら計算すれば同じ結果が得られます。
これは「解き方の違い」なので、「どちらが良い」はなく、試験では両方とも○になります。
ところが、「混ぜて半分」は「半分にしてから混ぜる」と同じという発想の方が、
採点者これは大事なことに気づいていて、
とても良い！
採点者は、好感を持って採点するでしょう。
対して、未知数を置いて方程式でガンガン解いている答案を見ると、
採点者まあ、これは
これでいいんだが・・・
採点者これは中学一年でやってくれれば良い
ことで、小学生らしい方がいいかな・・・
数学の教師である採点者は、こう考えるでしょう。
やはり小学生の間は、受験といえども「算数は算数的思考で」考えた方が、将来的にも良いと思います。
方程式の良いところは「未知数を設定すれば機械的に解くことができる」ことです。
この意味では、「あまり考えなくても、機械的発想で解ける」傾向もあります。
これは数学的発想としては極めて有効で、代数学の根幹ともいえます。
ところが、柔らかな発想を発達させるべき小学生の間に、
男子小学生未知数を置いて、
とにかく計算すればいいんだ！
「機械的発想」を覚えてしまうと弊害があります。
男子小学生機械的発想の方が
早いし、便利！
このように「算数・数学の本質を誤解」してしまう可能性ががあります。
算数は結構奥深くて、ある程度数学ができる人にとっても「困難な算数の問題」は沢山あります。
塾講師数学の発想を先取りすると、
中学受験の算数が楽に解けます！
このような考えもありますが、「小学生は小学生らしく」が良いように思います。
採点者側の視点として、記述式試験でガリガリ方程式で立式している子よりも、
出題者やっぱり、算数は算数らしい
発想の方がいいな・・・
算数の発想の子の方が望ましいでしょう。
「算数らしい発想で解いている」子の方に良い点をつけたくなるでしょう。
「比較的簡単な未知数設定」ならば、①などの簡単な方程式で解くのが良いでしょう。
ところが、複雑な問題を「とにかく方程式で計算して解いている」と、
採点者ここまで、方程式で
やらなくてもいいんだが・・・
「方程式で解いて減点」はなくとも、場合によっては、
採点者減点はしないが、うちの学校には
柔軟性を持った子の方が良いな・・・
このように「柔軟性優先」と考えるかもしれません。
「算数の範囲を超えた方程式で解いているから」といって減点するかどうかはわかりません。
基本的に「小学生は小学生らしく」の方が微笑ましく、採点者に好感をもたらすでしょう。
合否は「点数のみ」ではなく、特にボーダーラインでは「合格者を選出する」プロセスがあるでしょう。
採点者A最終的に、どの子を
合格としようか・・・
この時、「算数的な柔軟な発想が出来ている」志願者に対しては、
採点者AこのAくんは、点数が
少し足りないかもしれないが・・・
採点者A一生懸命、図を描いて
柔軟な発想をしている・・・
採点者Bじゃあ、そのAくんは
合格としたいな・・・
このように、中高の教員は考える可能性があるでしょう。
こういう発想があるとしても、非常に算数ができる子で「数学的発想が出来ている」子は例外です。
採点者AこのBくんは少し方程式を多用しすぎるが、
数学的発想が出来ている・・・
採点者Bまあ、数学的発想が出来ているなら、
将来性高そうだから、Bくんも合格かな・・・
中学受験の時=小学生が「数学的発想」を身につけることは大変困難です。
さらに、「数学的発想」は中学以降に身につければよいので、「算数的発想」を大事にしましょう。
基本的には「算数は算数らしい」柔軟な発想を学びましょう。
そして、この「算数的柔軟な発想」をしっかりと発展させて、応用力を身につけましょう。
特に受験期後半から直前期は、図や絵を描いて、
女子小学生ここは
こういう風に考えると良さそう・・・
女子小学生あ、だから
こことここの違いがポイントなんだな・・・
様々な解法を学んだ今こそ、「算数的柔軟な発想」を総合的にアップさせましょう。
すると、難問も解けるようになり、合格に大きく近づくでしょう。
さらに、この「算数的柔軟な発想」を身につけた方の方が、中学生以降も伸びる子になるでしょう。
次回は下記リンクです。
