直前期に図形問題が解く力を上げるコツ〜「直感的に明らか」を説明・基本的図形の性質を総復習・図形を多角的に考える姿勢・(2)解法B〜｜武蔵中1984年算数2・過去問・中学受験

前回は「対称性がある図形問題を解くコツ〜「正〜角形」の時は対称軸に着目・「思い込み」で問題を解かない・条件を整理して着実に・算数の記述のコツ・未知数や方針を明記〜」の話でした。

直前期に図形問題が解く力を上げるコツ：「直感的に明らか」を説明

ms18_01ts

前回は、上記の「正三角形が二つ+それぞれの中心が一致」する問題を考えました。

この問題は一見簡単そうですが、きちんと解くには相応の学力が必要です。

図形問題は「見るからに複雑で難しそうな」問題があります。

一方で、「簡単そうに見える」問題ですが、考えてみると「なかなか分からない」問題もあります。

前者の「見るからに複雑で難しそうな」問題は、解いてみたら意外と解きやすい事があります。

後者の「簡単そうに見える」問題は、簡単であったり、意外と分からないことがあります。

今回は、直前期に図形問題を「どう学ぶのが良いか」の話です。

ms18_105ts

この問題では、上の「正三角形アとウに着目」することが鍵でした。

このうち、「正三角形ア」は問題で与えられています。

「正三角形アとウは全て同じ（合同）」であることは、直感的に分かります。

算数や数学では「直感的に明らか」であることは大事ですが、それを説明できる姿勢が大事です。

前回は「折り返しても同じ直線=対称軸」を三本見つける話をしました。

ms18_102ts

ms18_103ts

ms18_104ts

これら三本の「折り返しても同じ直線=対称軸」が、解く鍵となります。

「折り返しても同じ直線=対称軸」から「正三角形アとウは全て同じ（合同）」を明確に意識しましょう。

基本的図形の性質を総復習

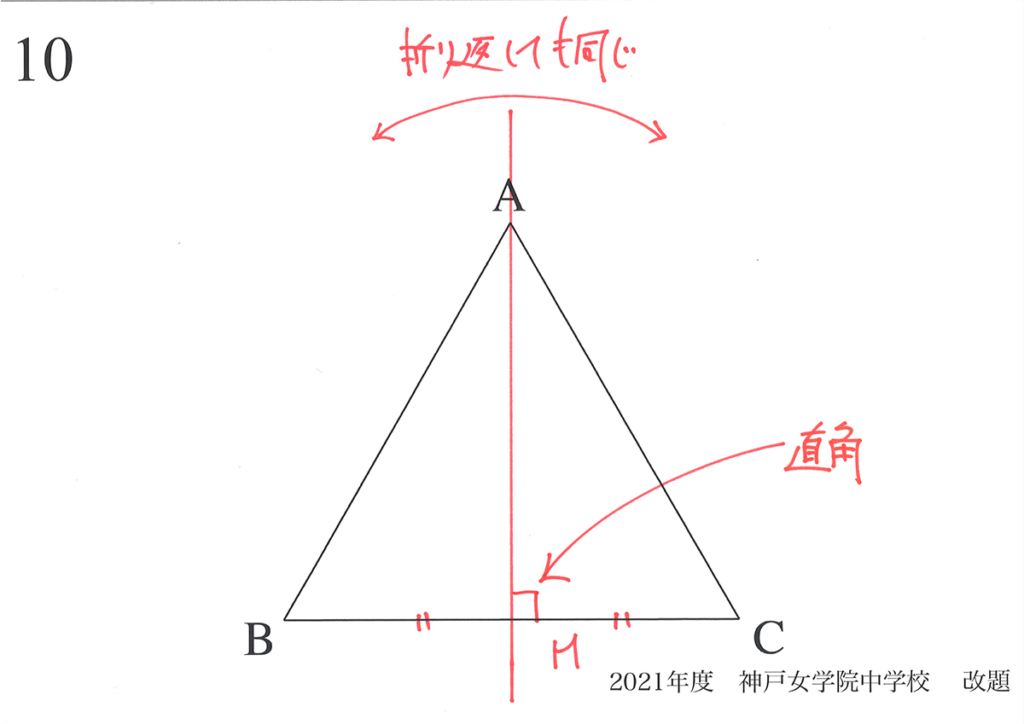
「正〜角形」が登場する図形問題は多いですが、中でも正三角形と正方形は頻出です。

それは、「正三角形と正方形が非常に強い性質を持っているから」です。

上の正三角形では「折り返しても同じ直線=対称軸」があり、向かい合う辺と直角に交わります。

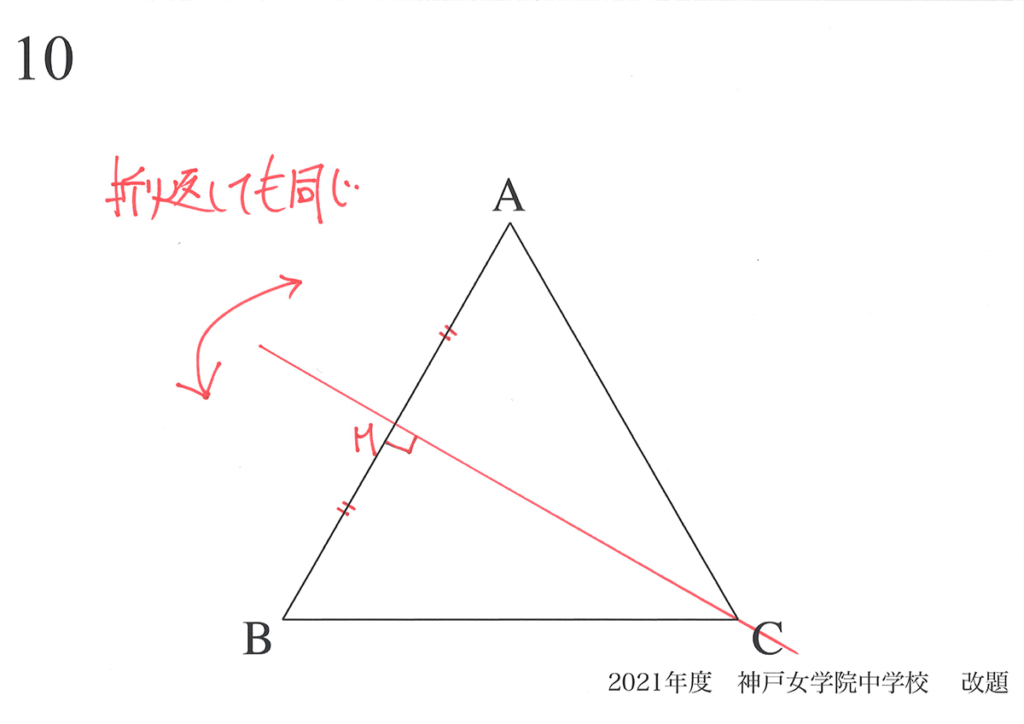
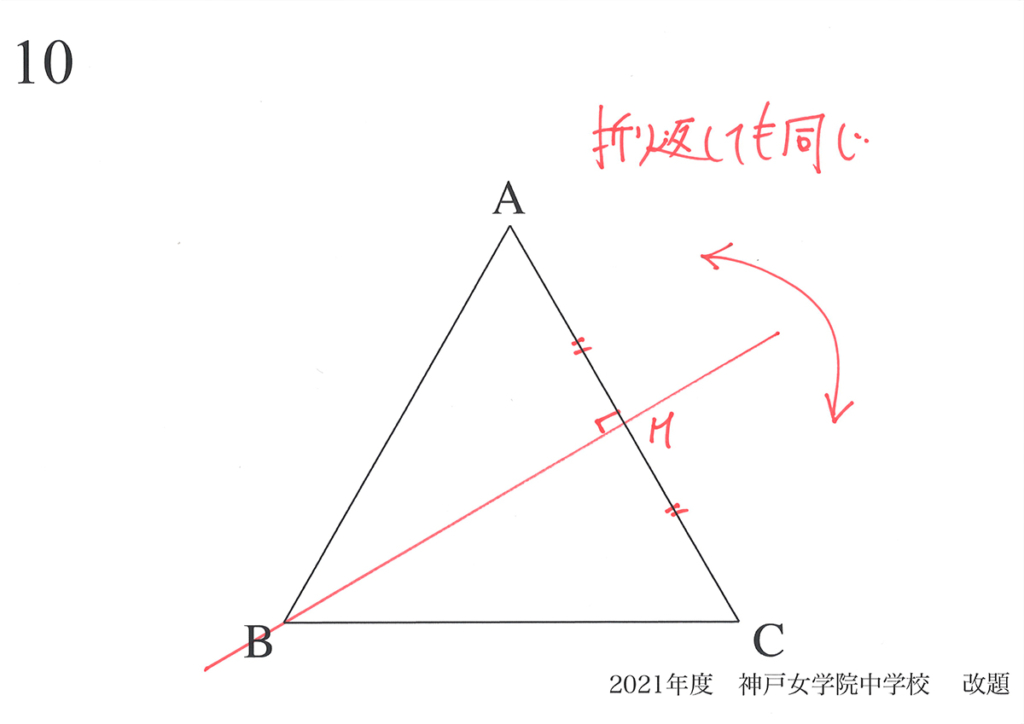
この「折り返しても同じ直線=対称軸」は、他に二つあり、合計で三本あります。

「対称性」という言葉が難しければ、「折り返しても同じ」と理解しましょう。

算数の記述の時、「対称性」という言葉ではなく「折り返しても同じ」と記載しても良いです。

動く点と正三角形の問題を解くコツを、上記リンクでご紹介しています。

ms18_104ts

「正三角形二つ」と「正三角形一つ」で、「折り返しても同じ直線=対称軸」が同じ理由を考えましょう。

今回の問題で大きな特徴は、「二つの正三角形の中心と対称軸の向きが同一」であることです。

この問題では、条件の設定のために「折り返しても同じ直線=対称軸」が描かれています。

「正〜角形」では、中心や対称軸がとても大事です。

特に「正〜角形」にとって「中心は図形のへそ」みたいな感じで、極めて重要です。

図形問題で「正〜角形」が登場したら、

必ず「図形の中心に着目」するようにしましょう。

このように、様々な問題を解いた直前期は、「基本的図形の性質を総復習」すると良いでしょう。

図形を多角的に考える姿勢：(2)解法B

ms18_119ts

前回は、（２）のイの面積を求めるために、上のように「イ＝ア＋エ」で考えました。（解法A）

イの面積を求めるために、他の方法を考えてみましょう。

ms18_123ts

問題の図形の大きな特徴である「二つの正三角形の共通の中心」に着目しましょう。

すると、上の図形のように「大きな（36cm2）正三角形の１/６の図形=オ」が見えてきます。

そこで、「イ＝アの半分＋オ」で解いてみましょう。

ms18_124ts

まずは、「オの面積」を求めれば、（１）の面積の半分を加えれば「イの面積」が計算できます。

ms18_125ts

このように、別の視点から「イの面積」が求まりました。（解法B）

解法Aは「ダイレクトに（１）を利用して考えている」点で、やや素直です。

一方で、「正三角形の１/６」に着目する解法Bも良いので、どちらでも良いでしょう。

図形問題は「複数の考え方・解法」があることが多いです。

直前期には、問題集などの解法を学ぶだけではなく、

「多角的に考える」姿勢で学ぶと、総合的な学力が上がるでしょう。

図形問題に限らず、

様々な分野の問題で「少し違う視点」を考えると、色々な気づきが生まれます。

直前期は、総まとめで「多くの問題を解く」ことも大事かもしれません。

「しっかり理解して復習」と「少し異なる視点で考える」姿勢で、総合力と瞬発力を高めましょう。