前回は「合格の秘訣〜単なる計算問題に対する姿勢・冷静になっても計算問題でつまづいた時・瞳を閉じて「仕切り直し」・どうしても計算問題が上手く行かない時・切り上げて次へ〜」の話でした。
算数の大問で「つまづいた」とき：最初に「全体を見渡す」大事さ
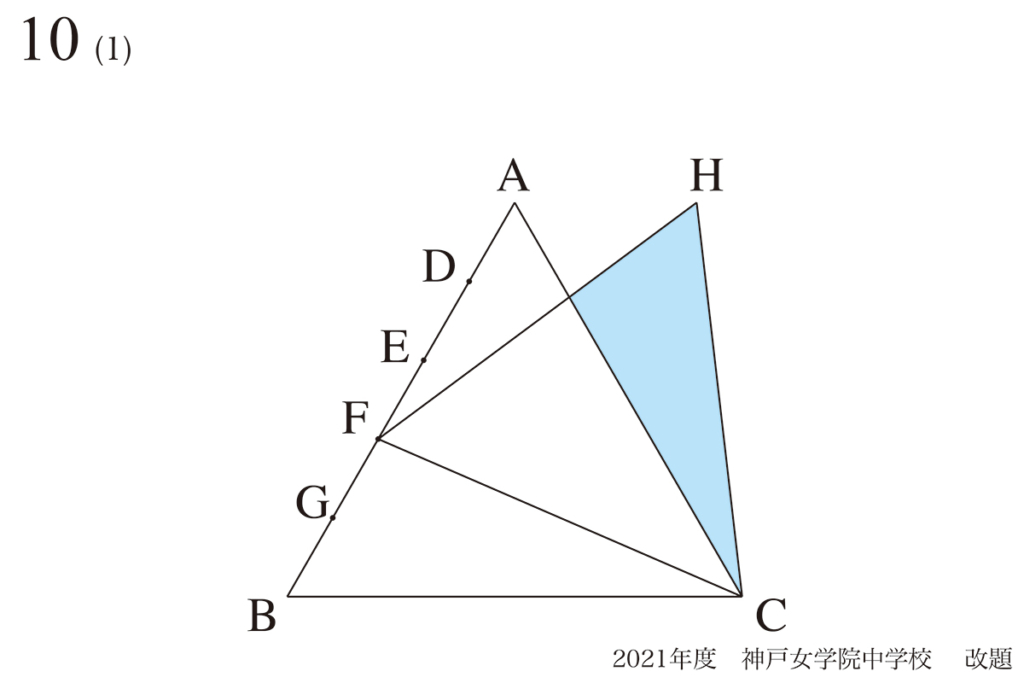
今回は算数の大問（小問が2題以上）で、ちょっとつまづいたときの効果的対処法の一つのご紹介です。
算数実践問題10で、「二つの正三角形」の問題を考えました。
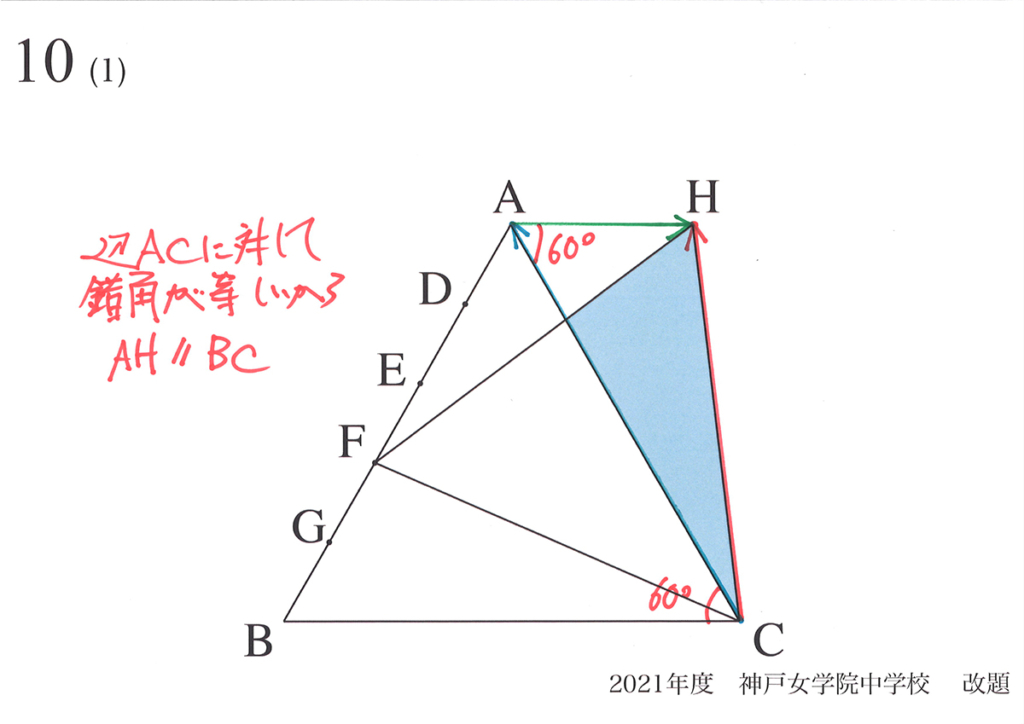
この問題を解くとき、「図形の辺を矢印で考える」考え方をご紹介しました。
あるいは、「同じ角度を見つけていって、相似形を発見する」姿勢でも良いでしょう。
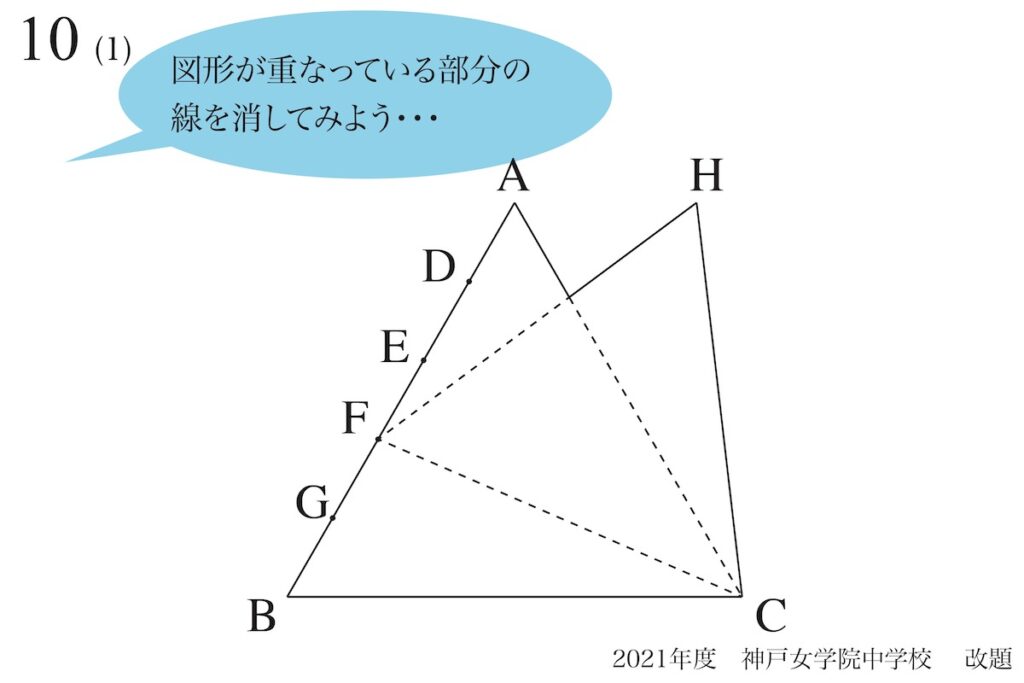
「簡単な図形が複数って分からない」時は、「図形の線を消して、全体を見る」視点も良いでしょう。
いずれの問題でも、「何らかの発想」を思いついて解ければ良いです。
このような大問を解く際には、
小問が2つある
問題だな・・・
まずは(1)を
解いて・・・
よし、出来た感じだから、
次は(2)へ・・・
と考える方が大多数でしょう。
このとき、「まずは(1)出来る」のが望ましいですが、実際には、
あれ、(1)が
分からない・・・
う〜ん・・・
困ったな・・・
解ける糸口が
見つからない・・・
何か良い
補助線があるはずだけど・・・
このように、「解法の糸口が見つからなく、(1)がうまく解けない」こともあるでしょう。
こういう時は、
(1)が出来ないなら、
(2)には進めないから・・・
仕方ない・・・
他の問題へ進もう・・・
と切り上げて、「他の問題を解いて、合格点を目指す姿勢」も考えられます。
大問が複数あることが多い算数の問題では、「最初に試験全体を見渡す」ことが大事です。
こういう時は、最初に全体を見渡しておけば
そうだ・・・
あの問題なら出来そうだから、そっち行こう・・・
と考えられますが、「最初に全体を見渡してない」と、
う〜ん、
次はこっちかな、あっちかな・・・
取り組む問題に対して、右往左往してしまうことになってしまう可能性が高まります。
問題の最初の方で「つまづく」可能性は誰にもあり、むしろ「つまづかない」可能性の方が小さいです。
「大問の初期段階でつまづく」可能性は「ある」ので、「最初に全体を見渡す」ようにしましょう。
・試験が始まったら、すぐに1問目に取り掛からないで、全体を見る
・「全体を見る」時間は「1分程度」で、個人差があるので事前に決めて、イメージしておく
例えば、算数の試験で問題が1,2,3,4・・・とある時。
「順番通りに1,2,3,4とやらなければならない」のではないので、
ここは2,3,4,1の
順にしようかな・・・
旅人算の3は得意だから、
3,2,1,4の順が私はいいかな・・・
試験冒頭の1分程度で全部を見渡して、「解く順序」を決定しましょう。
視野を広げて考える戦略的思考
この「全体を見渡して、問題を解き始める」時、
よしっ！まずは(1)だから、
(2)以降は読まなくていいや！
複数の小問に対して「(1)のみを読んで考える」方が多いでしょう。
上図のように「(2)以降の問題文が記載されているのに、先は見えていない」状況が多いです。
「少し先の問題文を読む」方でも、
(1)が出来なければ、
(2)は出来ないだろうから、読んでも仕方ないし・・・
「(2)以降はあまり見えていない」上のような状況の方が多いでしょう。
試験の際には「集中する」方が多いので、「集中しすぎて、目前の問題しか見えない」状況になりがちです。
問題文は「全体を見渡す」ことが大事ですが、「先の問題を読む」ことも大事です。
問題を解くときは、
(1)の問題は
〜を求めればいいんだ！
よし、早速
やってみよう！
と考えて、「ドンドン(1)から解く」のも良いですが、
そういえば、(2)は
どんな問題だろう・・・
と少し考えて、問題文の先を読んでみましょう。
一つのテーマの大問の中の小問は、「お互いが関係がある」事がほどんどです。
逆に「お互い無関係である小問」は考えにくく、あるとしても極めて少ないでしょう。
出題者は、
この問題では、
最終的に、このことを考えて欲しい・・・
一気にこれが出来るのは
難しいから、少しヒントを出そう・・・
と考えています。
多くの場合「前の小問が後ろの小問のヒント」ですが、「後ろの小問が前の小問のヒント」となることもあります。
あれ、(1)が
よく分からない・・・
と少しつまづいた時こそ、
(2)の問題を読んでみて
ヒントはないかな・・・
と考えてみましょう。
あ、
ひょっとしたら・・・
と「何か気づく」事がある可能性があります。
分からない・・・
う〜ん・・・
と悩んでばかりよりも、「先の問題文を読む」ことでヒントが得られることがあります。
この姿勢は「視野を広げて考える戦略的思考」とも言えます。
試験で問題を解くだけでなく、実社会でも通用する大事な考え方・姿勢です。
・大問を解く際は「順番に問題を読んで解く」ではなく、小問の問題文を全部読む
・他の小問が「ヒントになっている」可能性があり、視野を広げる事が大事
試験本番で算数の問題が解ける発想：問題文の先を読んでヒントを得る
この「問題文の先を読んでヒントを得る」発想の具体例を考えてみましょう。
算数実践10で(1)を考えて、
う〜ん、
イマイチ分からないな・・・
上のように「ポイント・解く鍵にたどり着かない」状況を考えてみます。
この時、
補助線は
どこに引いたら良いだろう・・・
「良い補助線」はありますが、なかなか見つからないこともあります。
こういう時は、先の小問を読んでみましょう。
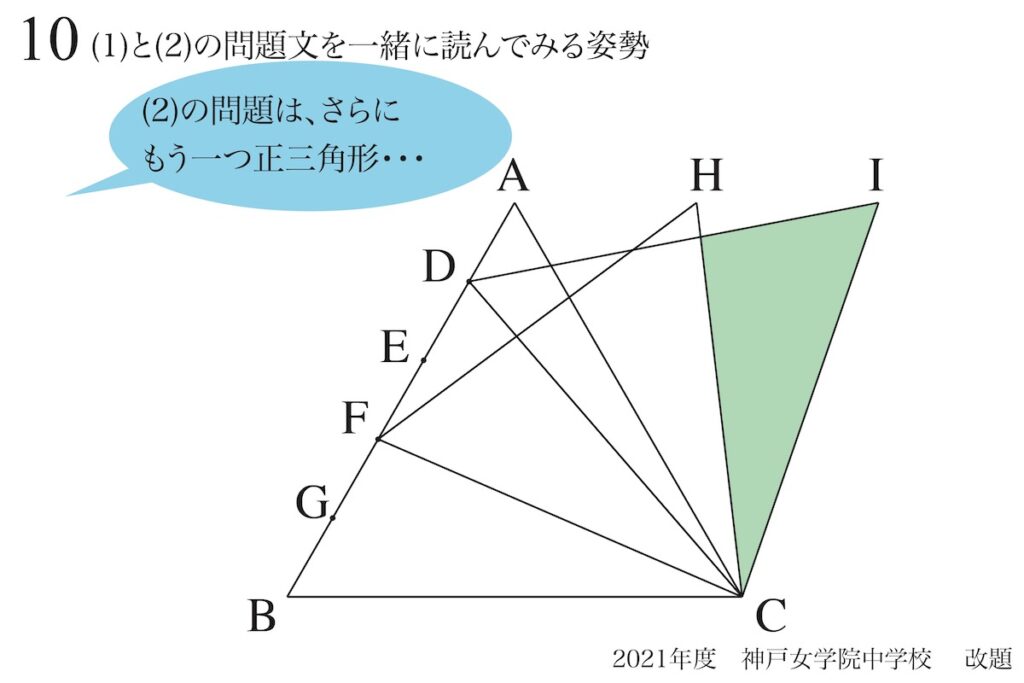
(2)では、さらに正三角形が追加されて、「緑色の部分の面積を求める」問題です。
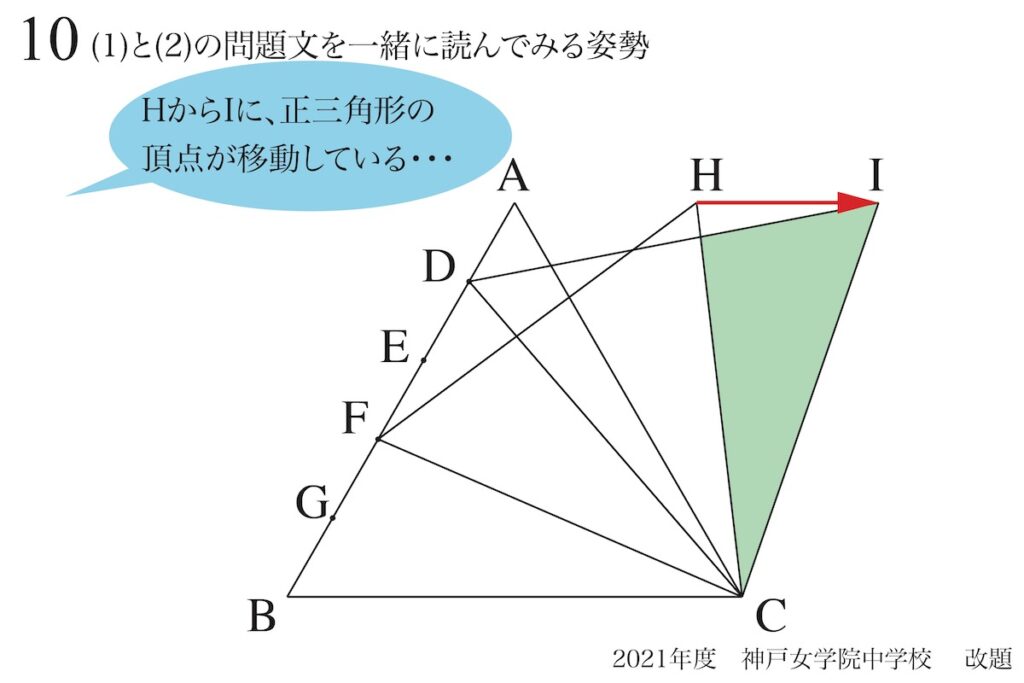
(2)になると、「正三角形が3つ」になって、複雑になりますが、右上の頂点が右にドンドン移動しているのに気づきます。
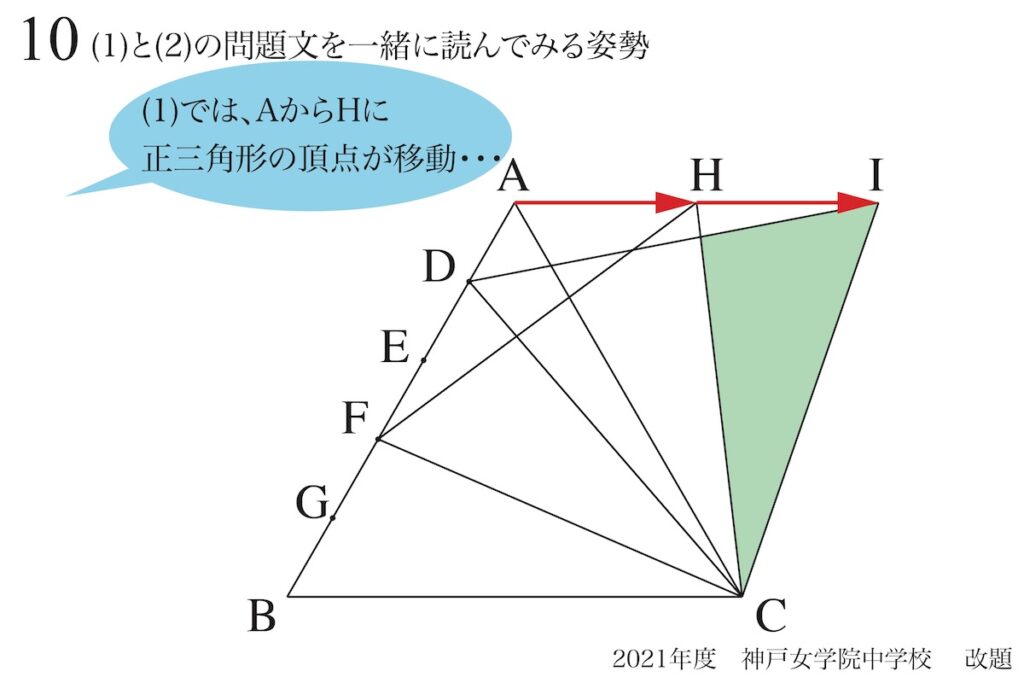
(1)と比較してみると、正三角形の頂点が次々移動しているのが分かります。
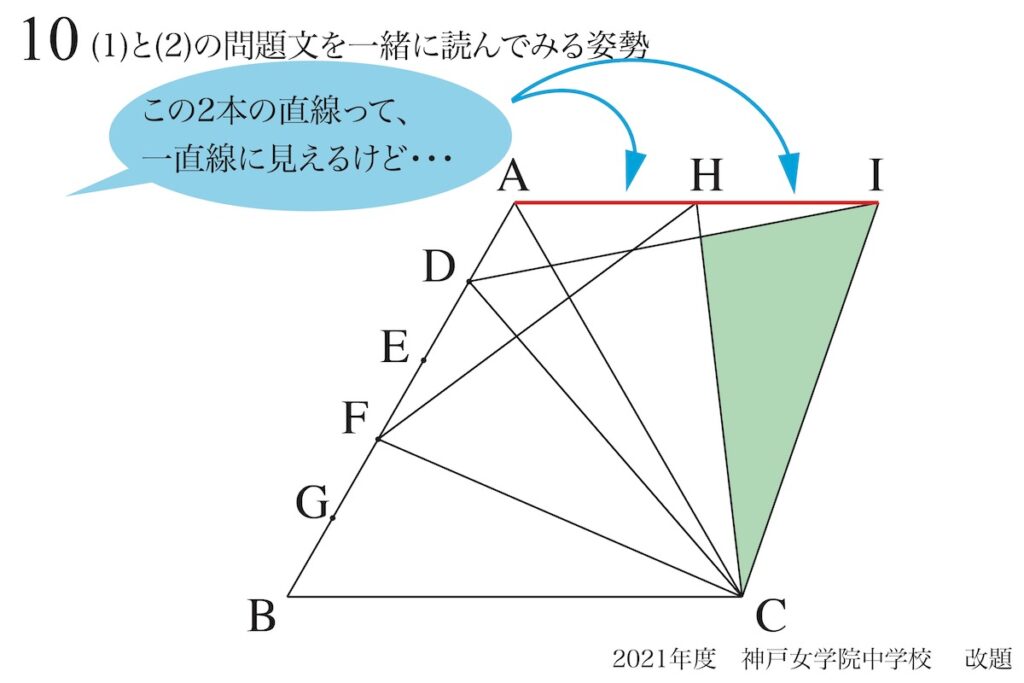
(1)と(2)は別ですが、どうやらこの直線AHとHIは「一直線」のように見えます。
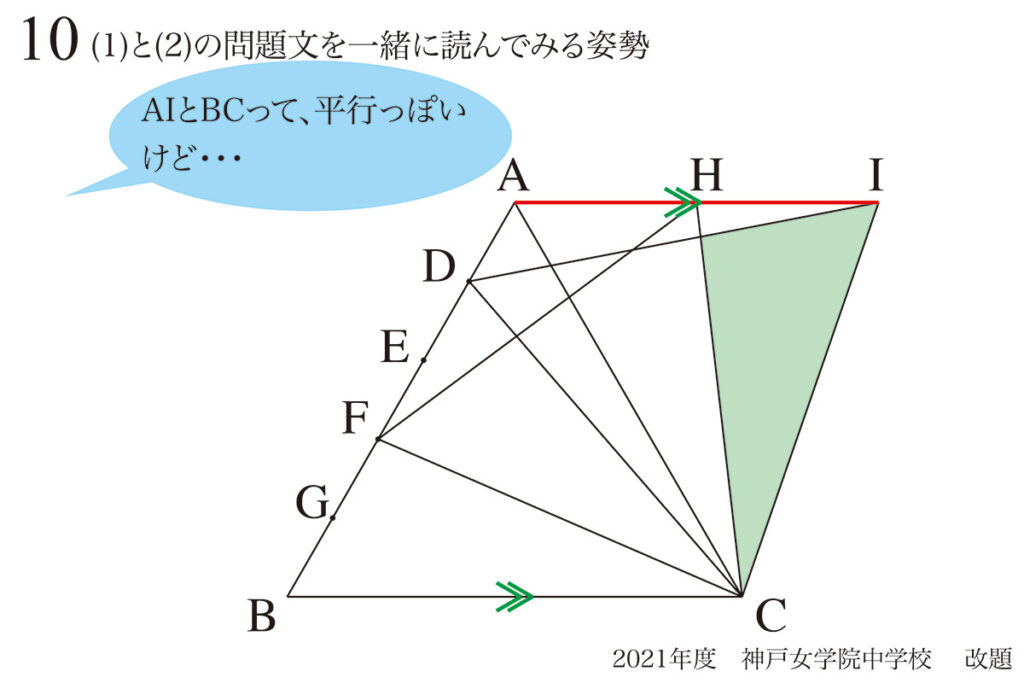
ここで、「平行な感じ」に気づける可能性があります。
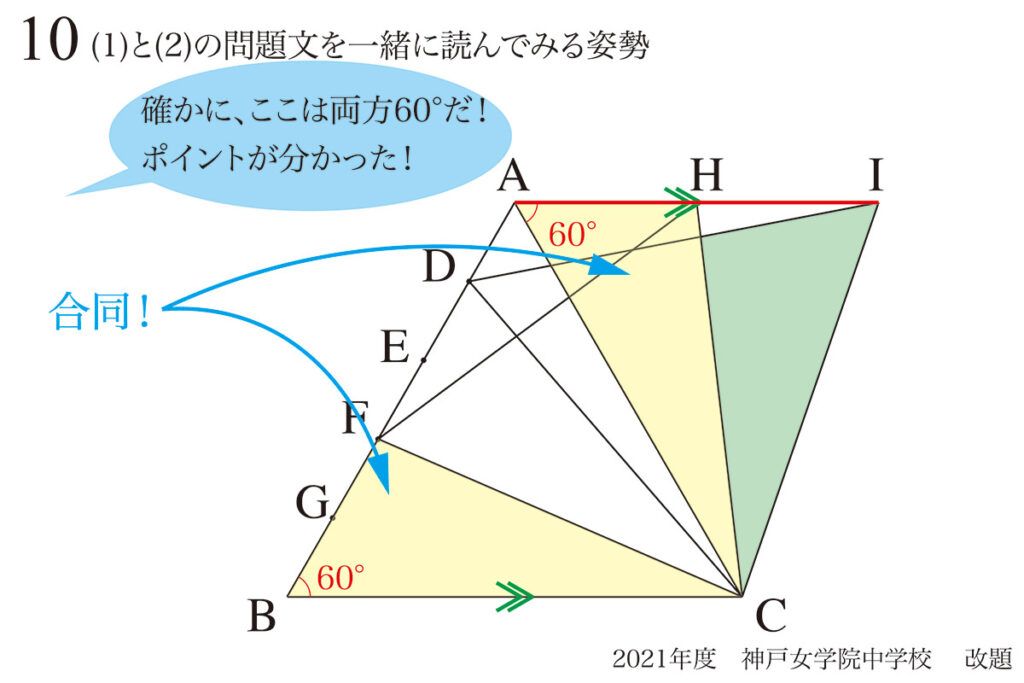
ここで、よく考えてみると「合同図形」が見つかり、「ポイント・解く鍵にたどり着いた」状況になりました。
ここから先の解法は、下記記事を参照してください。
算数の問題では「つまづいて、なかなか先が見えない」時、
ちょっと待って、
う〜ん・・・
と考え込んでしまうと、
あれ・・・
うまく出来ない・・・
すぐに2〜3分が経過してしまいます。
「(1)で悩んでいる」ときに、
(2)の問題文を
読もう・・・
と考えて「(2)の問題文を読む」のにかかる時間は、10秒以下が多いでしょう。
時々、小問の問題文が長い場合がありますが、20秒程で内容は分かりそうです。
「一分一秒が大事」な試験ですが「てこずって2〜3分経過」より「10〜20秒で先を読む」方がオススメです。
社会・国語と異なり、「問題文が簡潔」である事が多い算数。
文章題などで「全体の説明文」が長い場合でも、小問の問題文はそれほど長くない傾向があります。
意外と良いヒントが見つかる可能性が高い「問題の先を読む」姿勢。
ぜひ、算数の試験でやってみて下さい。
「試験本番で突然やる」のは難しいので、事前にこれまでの問題を復習する際に、
これ、(1)も(2)も(3)も問題文
知ってるけど・・・
「初めて見た」気持ちで
問題文を読んでみよう・・
(2)(3)の問題文から
なんとなく方向性が見えそうだ・・・
と予行演習しておきましょう。
・小問の問題文を10秒から20秒程度でサッと読んで「先を読む」姿勢
・問題同士の関係性からヒントを探して、問題の「解く鍵」発見へ
読者の受験生の皆様が、志望校に合格することを心より願っております。
