前回は「算数の理解力をアップする学び方〜「考える対象」を絞る思考法・思考する領域が広すぎる「中学受験の算数」・多数の学ぶ分野〜」の話でした。
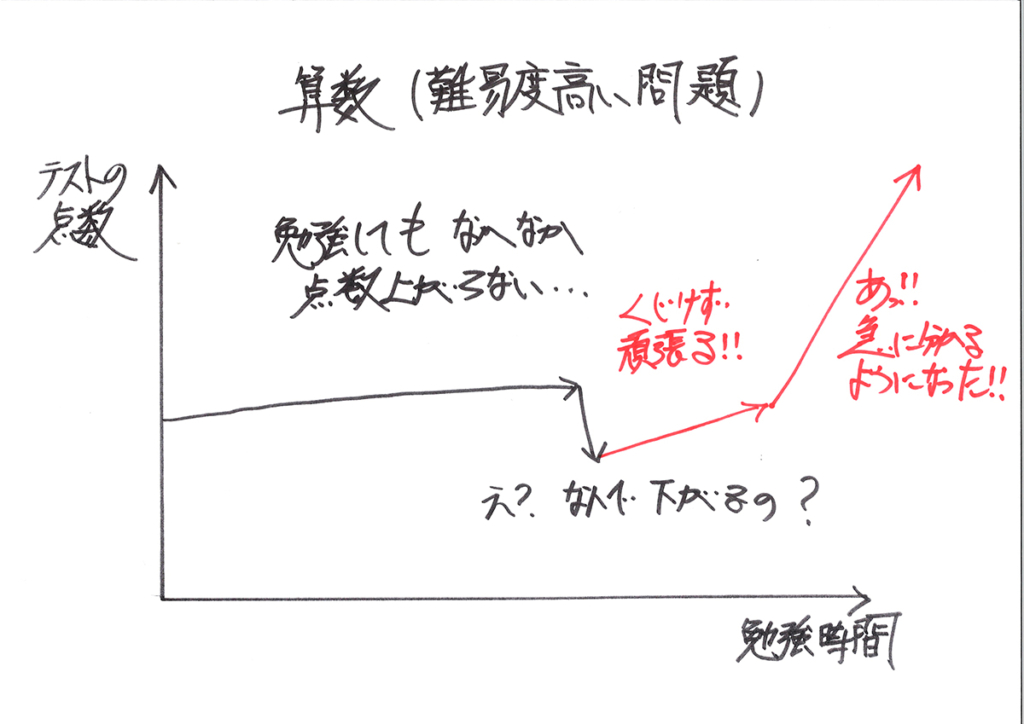
なかなか成績が上がらない算数:時には成績が下がる「謎の科目」
小学生まで「算数」と呼ばれている学習分野は、中学以降は「数学」と呼ばれます。
いわば、「数学の前座」の立場であるのが算数です。
そのため、「数学よりも簡単で理解するのが容易」なはずの算数は、実は奥が深い世界です。
特に「普通の算数」とは、別科目とも感じられてしまうほど違うのが「中学受験算数」です。
様々な難易度の問題がありますが、最難関レベルの問題は大人・大学生でも解ける方は少数派です。
 男子小学生
男子小学生算数は、勉強しても
勉強しても、なかなか出来るようにならなくて・・・



やっぱり算数は特殊で、
「頭の良さ」とかセンスが大事なのかな・・・
算数に対して、このように感じる中学受験生は大勢いらっしゃると思います。
算数の勉強時間と学力・点数に関する話を、上記リンクでご紹介しています。
「勉強すれば相応に学力・点数が上がる」理科・社会・国語などの科目。
それに対して、算数は一生懸命勉強しても、なかなか学力や点数に反映されない「謎の科目」です。
時には「勉強しているのに、成績が下がる」こともあるのが算数です。
難易度が高い問題が模試などで出題されて、出来が良くない時、答えを見ると、



なぁんだ・・・
こう考えれば、出来たんだ・・・



ここにちょっと補助線引けば、
全部分かったのに・・・
知識系の問題などでは、「知らなかったから出来なかった」など「出来ない理由が明確」です。
対して、算数は基本的問題は別として、答えを見れば「なぜ出来なかったのかが謎」な場合が多いです。



なぜ、この考え方に
気づかなかったんだろう・・・



やっぱり、もっと図形の問題
解けば、「補助線のセンス」が身につくのかな・・・
このように、難易度が高い問題に対しては、「基本的事項が分かっているのに解けない」算数。
この「難しい算数の問題に対する悔しい思い」は、筆者は良く分かります。



なんだ・・・
こう考えれば出来たんだ・・・



なぜ、試験中に、こう考えないで、
違う方向に行っちゃったんだろう・・・
もう35年ほど前のことですが、中学受験生だった筆者もまた、このような思いを持ったものです。

算数実践紀行では、様々な問題の「本質的考え方」をご紹介しています。
上記リンクでは、旅人算・比の問題の本質的解き方をご紹介しています。



やっぱり、算数は
中学受験生の時も良く出来たんでしょ・・・
筆者に対しては、このようなイメージを持つ方が多いかもしれません。
筆者は中学三年生くらいから数学が、かなり得意になりました。
数学が出来るようになると算数に対して様々な発想が生まれるので、色々な解き方をご紹介しています。
そして、運よく武蔵中学に合格した筆者ですが、



もうちょっと算数が
出来るようになりたい!
中学受験生当時、実は武蔵中学のように最難関レベルの中で算数の学力は「まあまあ」程度でした。
学力の測り方は「偏差値」ばかりではなく様々な視点がありますが、難しい算数が解けないと、



こういう難しい問題が解ける人は、
どういう勉強しているのかな・・・



やっぱり、たくさんの勉強時間で、
たくさんの問題を解いているんだろうな・・・
こんな風に思ったことを、今でも明瞭に覚えています。



いつも算数の成績が良い
A君やB君は、やっぱりセンスが高いのかな・・・
このように「出来ない理由」を考えてしまうのが受験生です。
そして、その気持ちは「当事者であった筆者」は痛いほど良く分かります。
ある程度は勉強している自信を持っていると、受験生は、



私は一生懸命勉強してるし、
算数の出来が違う理由は「センスの違い」かな・・・
このように誤解しがちです。
中学受験算数の出来とセンスの関係は、「無関係」とは言いませんが「大して関係がない」です。



結局、どう勉強したら、
点数や偏差値が上がるのだろう・・・
試験で「明確な点数・偏差値」が出てくる受験生にとって、やはり「点数を上げる」必要があります。
算数の学力アップのラストスパート:繰り返し「覚えてしまう」勢い

今回は、最難関校〜難関校受験を目指す方を対象です。
基本的な問題は少なく、ある程度難易度が高い問題の70%程度獲得を目指す方向けです。
分野にもよりますが、「比較的基本的な問題」は「その考え方」を固めるのが最優先となります。
複合的でハイレベルな問題が解けるようになる、直前期にラストスパートで算数の学力を上げる方法です。
この記事を書いている10月は「直前期」であり、多くの方が過去問に既に取り組んでいます。
上記リンクでは、過去問に対する学び方の話をご紹介しています。
過去問の算数の問題を解いて、



よしっ!
上手く出来た!
上手く解ければ良いですが、「来年の2月に70%程度出来れば十分」なので、



(1)は解けたけど、
(2)(3)は全然分からなかった・・・



ちょっと分からなかった・・・
解答見れば分かるんだけど・・・
10月の時期では、このような受験生が多いでしょう。
「解けないと悔しい」ですが、ここで解けなかった問題の解答を読んで、



ふ〜ん、
そうなんだ・・・



そっか、こうすれば
解けるんだ・・・
解答を目で追って「分かったつもり」になっても、何も学力は向上していない状況です。
ここで、解答を読んだら解答を閉じて、もう一度しっかりトライしてみましょう。
最初から「試験のつもりでしっかりノート・紙に書いて、解く」のが大事です。



もう一度「しっかり書いて解く」は
やってるよ!
こういう方は、「少しずつ学力が上がっている」状況です。
ここで、特に第一志望校の問題、特に良い問題を何度もトライしてみましょう。



他に沢山問題集や
宿題あるし・・・



同じ問題を何度もやって、
意味あるのかな?
難しい問題(良問)は、解けば解くほど考えれば考えるほど、様々な学びがあることが多いです。
何度もやって「覚えてしまう」くらいの勢いで、何度もやってみると良いでしょう。



武蔵の過去問は
一生懸命、何度もやってみよう・・・
10月頃は武蔵中志望者の中で「まあまあ」程度で、せいぜい「中の上〜中の中」くらいだった筆者。
特に10月以降は、一生懸命過去問を何度も解いてみて、



武蔵の過去10年くらいの
問題の解き方は全部覚えてしまった・・・
何度も何度も解いたので、「解き方を覚えてしまった=頭に入ってしまった」状況になりました。
こうなると、



こういう問題は、こういうところが
ポイントになって、こう考えると良さそう・・・
このように「覚えてしまうくらい考える」と違う世界が見えてくるようになります。
ここで大事なのは、「ただ丸暗記する」のではなく「(意図せず)覚えてしまう」ことです。
「算数の解法の丸暗記」は一定の意味がありますが、難問に対しては、あまり意味がありません。
難しい問題を何度も考えると、「問題にある本質的なこと」が「自分なりに理解出来る」ようになります。
ここで「自分なりの理解」が大事で、この理解の仕方は「万人に共通」はないと考えます。
ぜひ、第一志望校の算数の難問には何度も取り組んでみましょう。
・第一志望校の算数の難問には何度も取り組む
・「解法を覚える」ではなく「解法を覚えてしまった」状態になり、本質的理解深める




