相似形の性質と間違えやすいポイント〜テクニックより大事なこと・相似形は「お友達」・相似形の理由・分かる辺の長さを計算・分数と少数の計算のコツ・問題13(4)解法〜｜正方形の攻略4・中学受験

前回は「相似形を発見するコツ・ポイント〜全体を見渡して見えてくる解く鍵・同じ角度を探す・相似形と相似比・問題 13(4)解法〜」の話でした。

問題 13

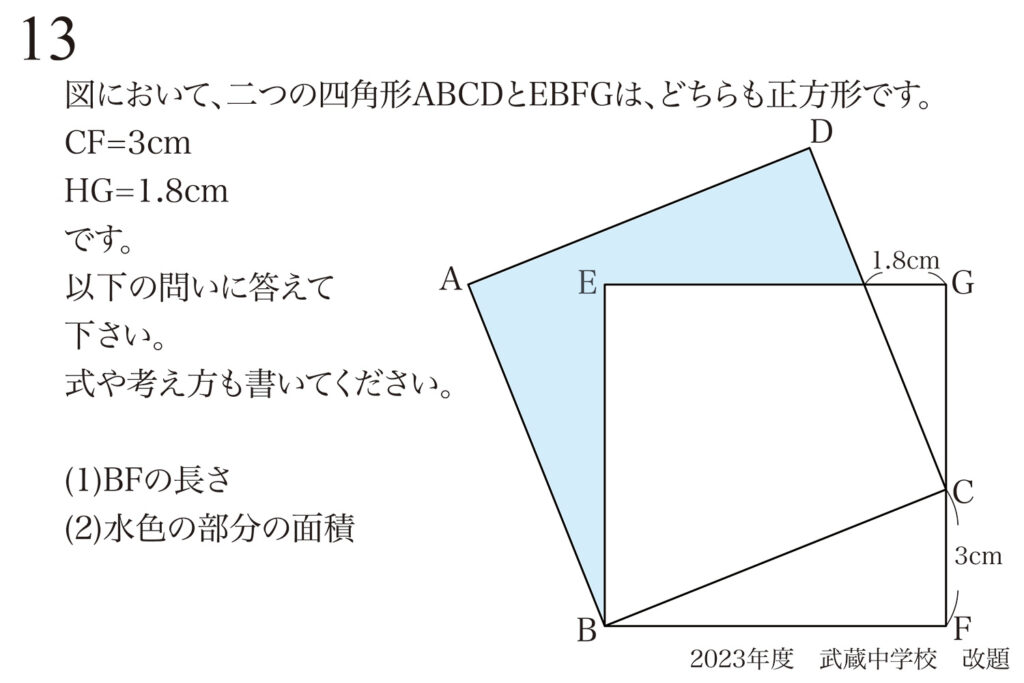
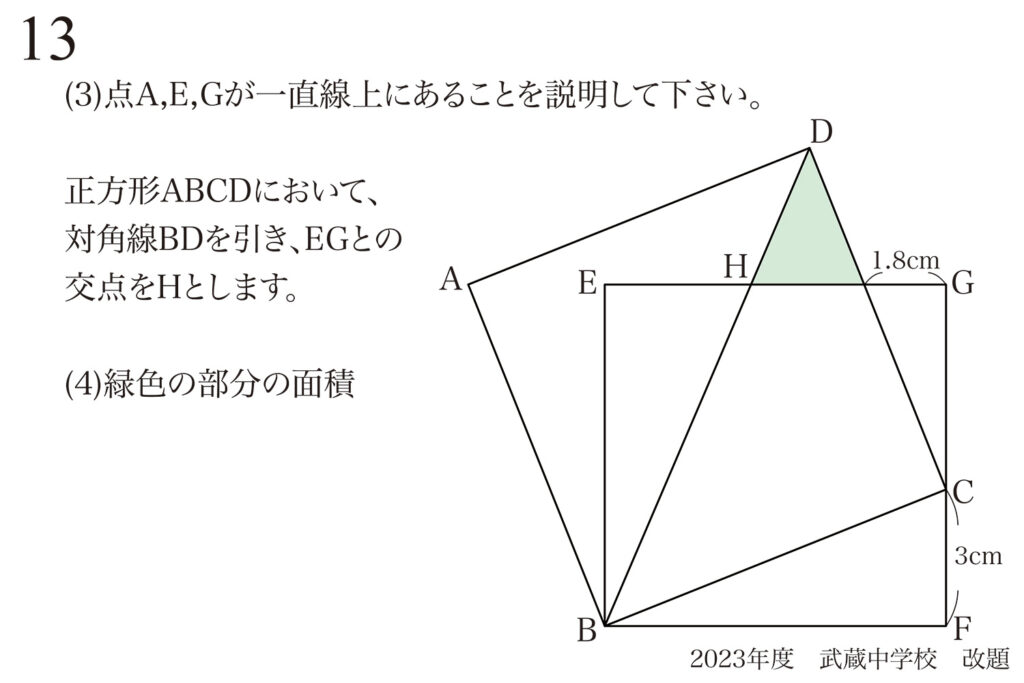
相似形の性質と間違えやすいポイント：相似形の理由

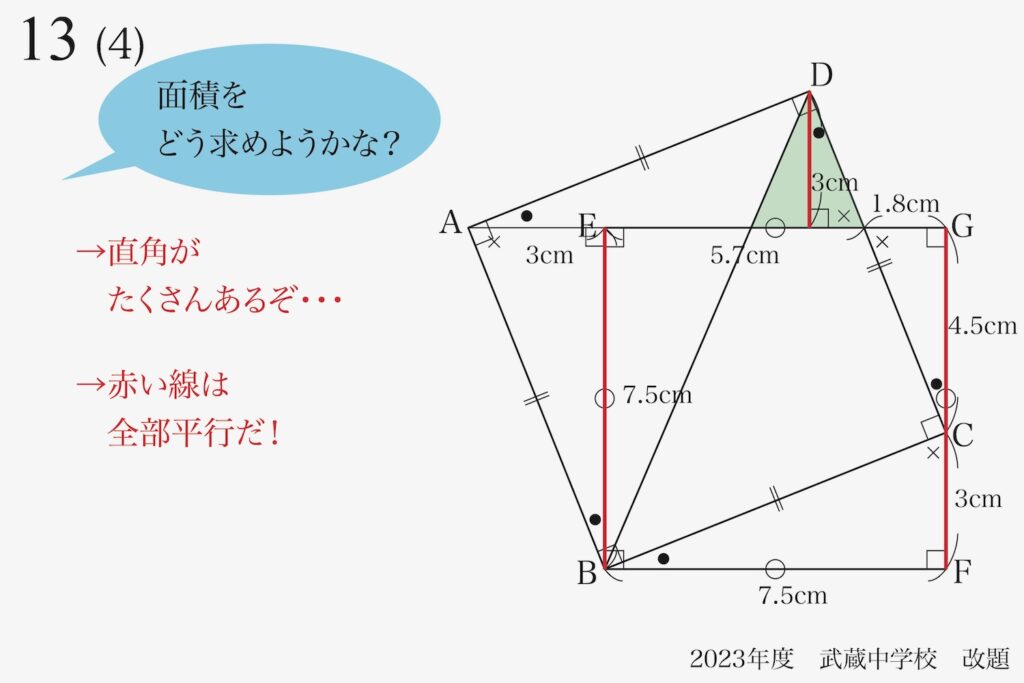
(4)の緑色の部分の面積を求めるために、相似形を考えて必要な辺の長さを求めることを考えます。

今回の図形は「2つの正方形」から出来ているので、直角が沢山あります。

直角があると、同じ角度が沢山ある傾向があります。

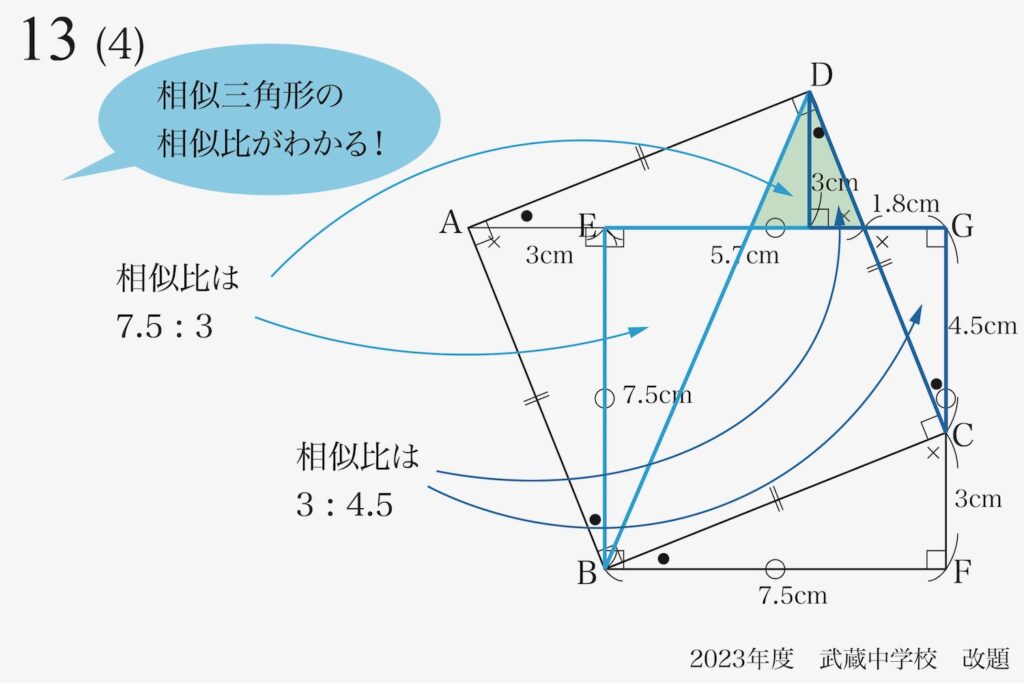
相対する平行な直線があると相似形が見えてきて、相似比がわかります。

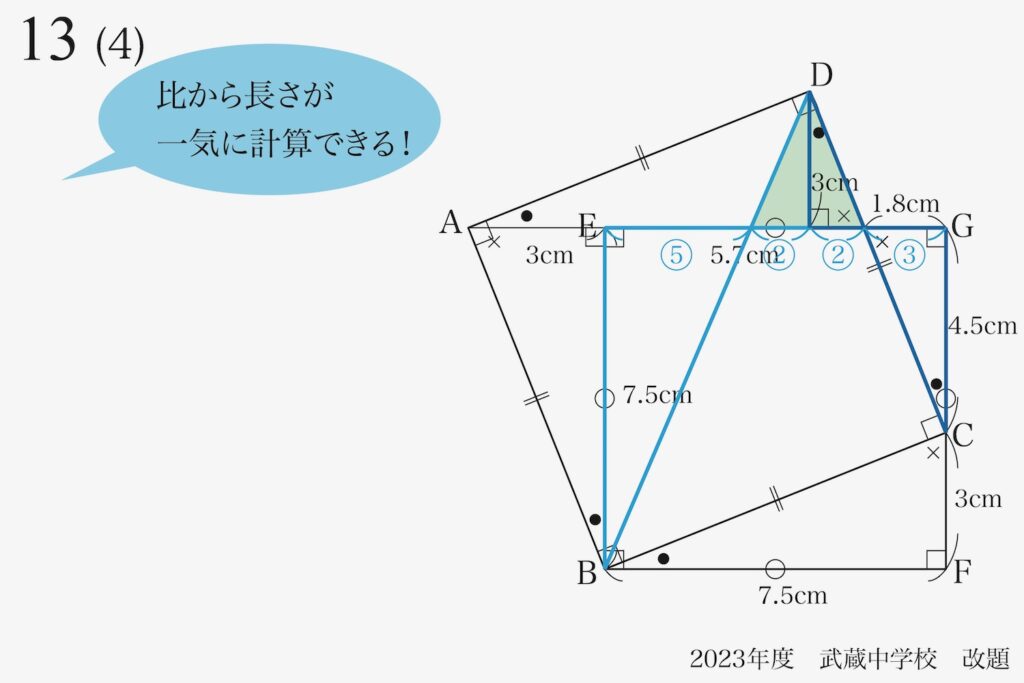
すると一気に相似比が計算できると考えます。

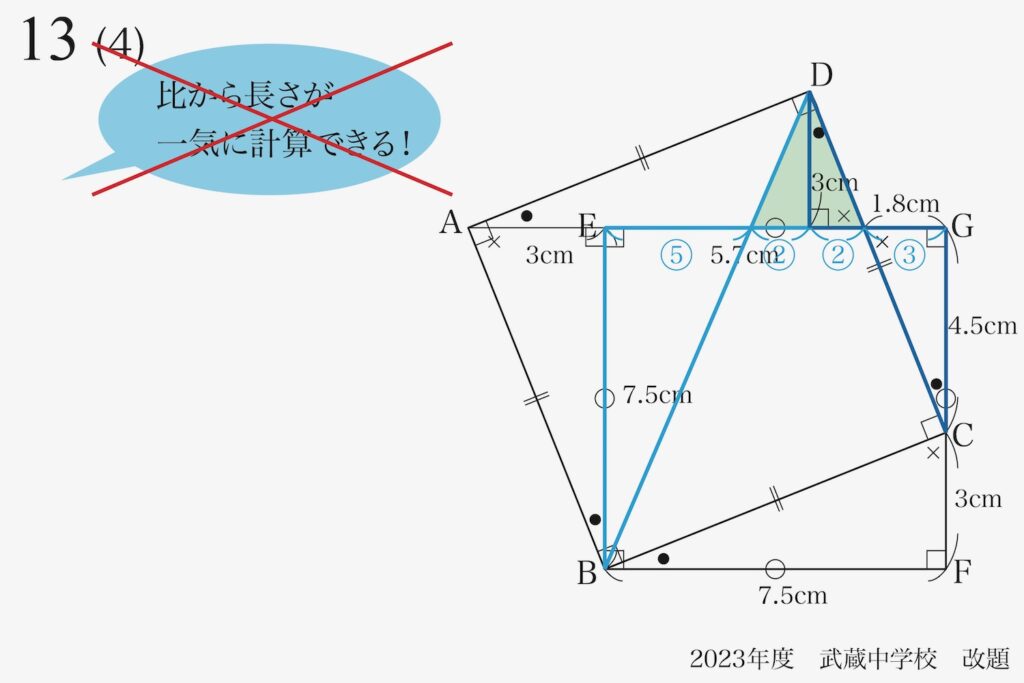
相似形が次々に見つかり、それらの辺の長さが「1.5の倍数」なので、一気に連比を求めました。

この考え方は間違っています。

このように「間違っていることが分かる」方もいらっしゃるでしょう。

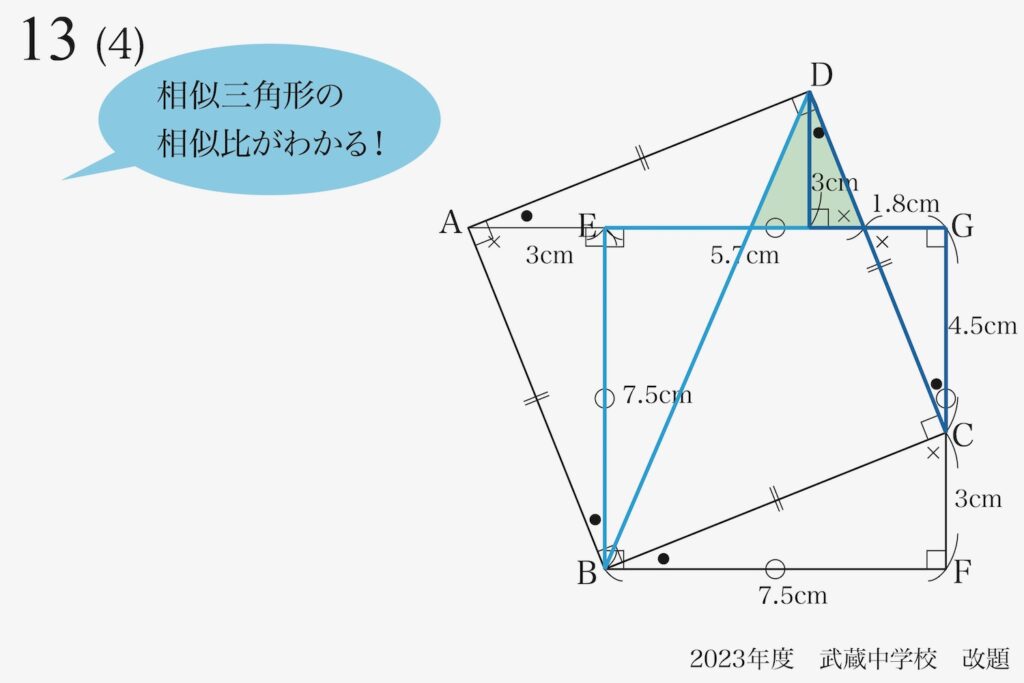
「分からない」という方は、もう一度、図形全体を見てみましょう。

相似形の基本（定義）をもう一度確認しましょう。

「同じ形」とは、何によって決まるでしょうか。

「同じ角度」を、しっかりと考えてみましょう。

「同じ角度」であることが、分かっているのは、今描きこまれています。

「描きこまれていない角度」は、まだ分からないのです。

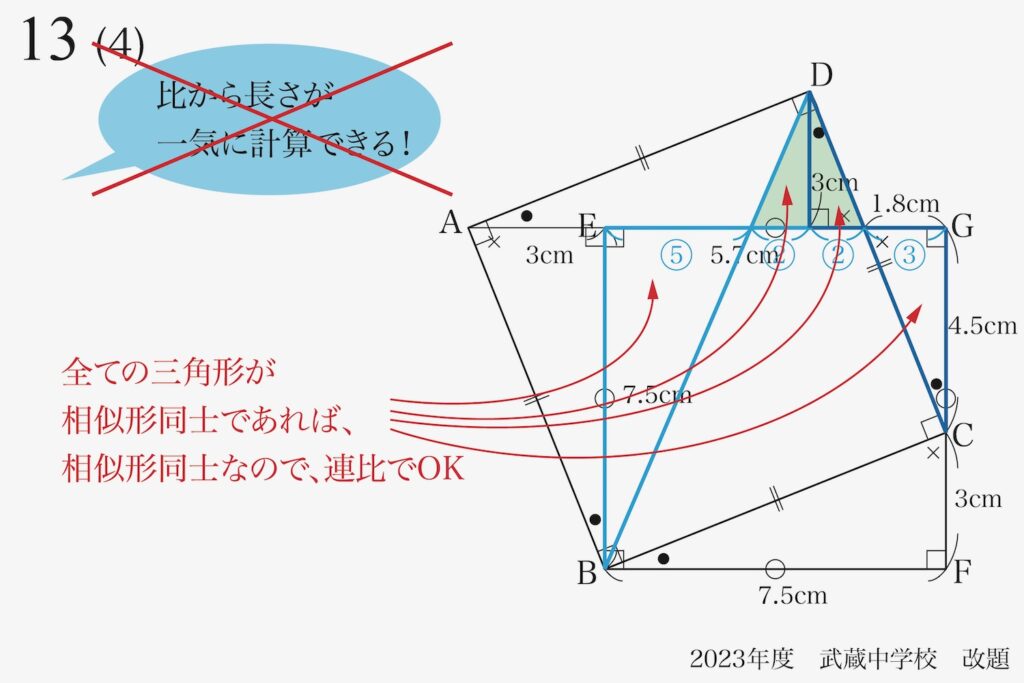
「三つの直線が平行」である三角形の「全てが相似形同士」であれば、先ほどの「連比」でOKです。

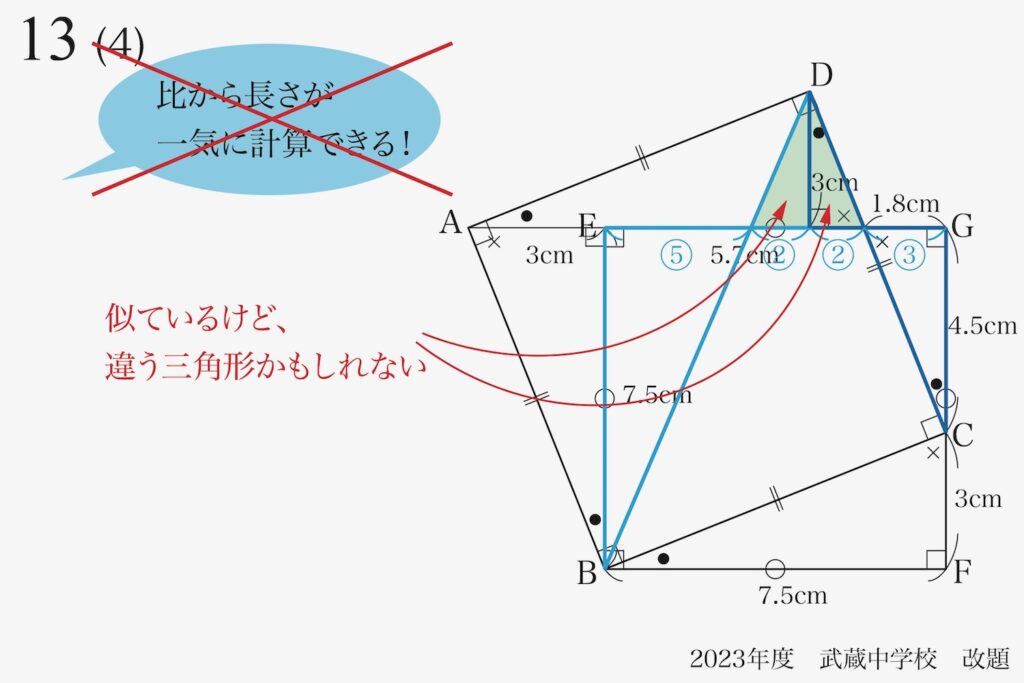
ところが、上の図で矢印の先にある二つの三角形は「一見似ている」のですが、違うかもしれません。

この二つの三角形が「相似形」であるかは、まだ不明です。

テクニックより大事なこと：相似形は「お友達」

これは、「言われれば、当たり前」のことかもしれません。

今回、勘違いしやすいのは、「全ての辺の長さが1.5の倍数」であることです。

「1.5の倍数（15の倍数）」は、数ある倍数の中でも、比較的「見えやすい倍数」です。

そのため、こういう数字を見ると、

こう勘違いしやすい数字です。

また、二つの三角形が「ほとんど似ている」ので「相似形である」と誤解しがちです。

「相似形」というのは、「図形のお友達」です。

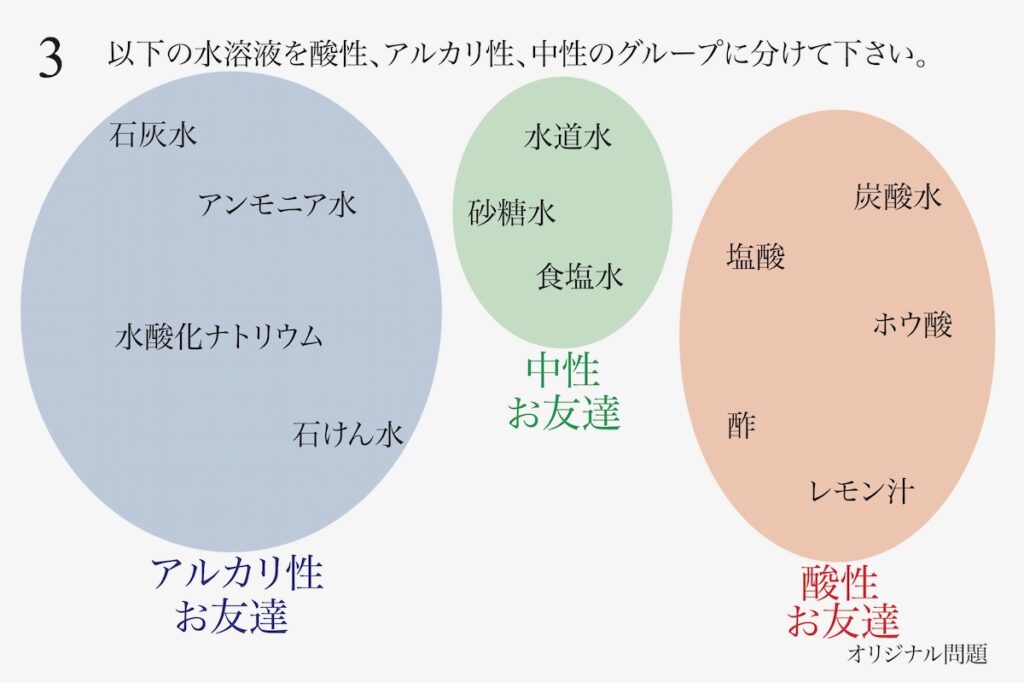
酸性・アルカリ性・中性と同じように、「同じこと（性質）がある」からお友達なのです。

そこで、「お友達である=相似形である」かどうかの判断は、しっかり見てあげましょう。

図形問題でも、どんな問題でも、テクニック・コツはあります。

一方で、その「解法のテクニック」に走りすぎると「大事なこと」を見落としてしまうことがあります。

「大事なことは見落とさない」姿勢は、基本的で非常に大事なことです。

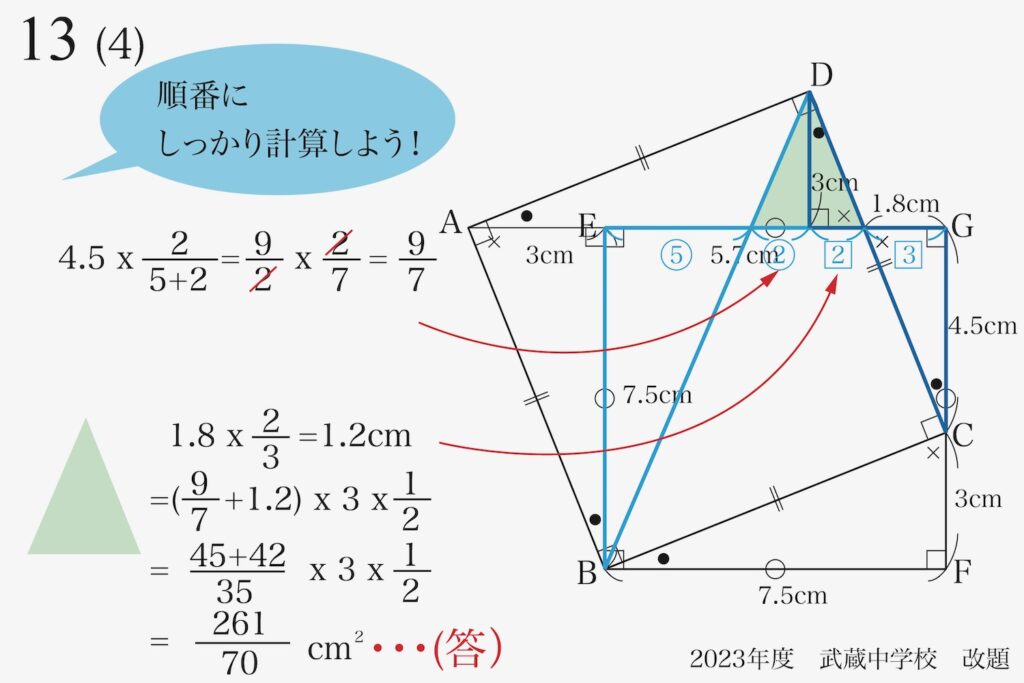
分かる辺の長さを計算：分数と少数の計算のコツ

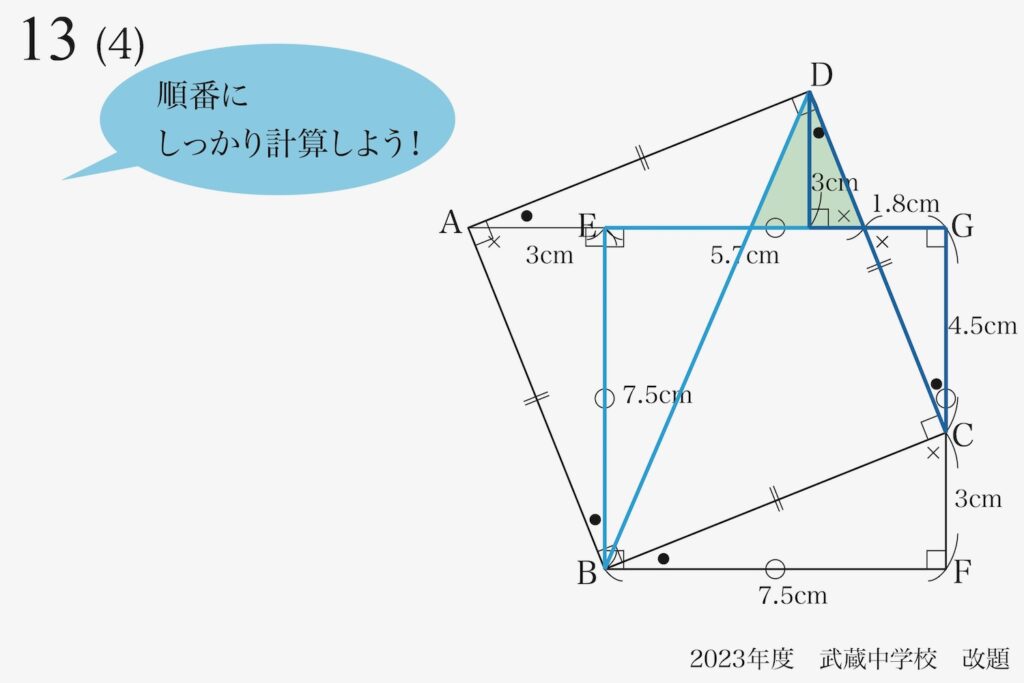
「一気に解く」ではなく、順番にしっかり計算してゆきましょう。

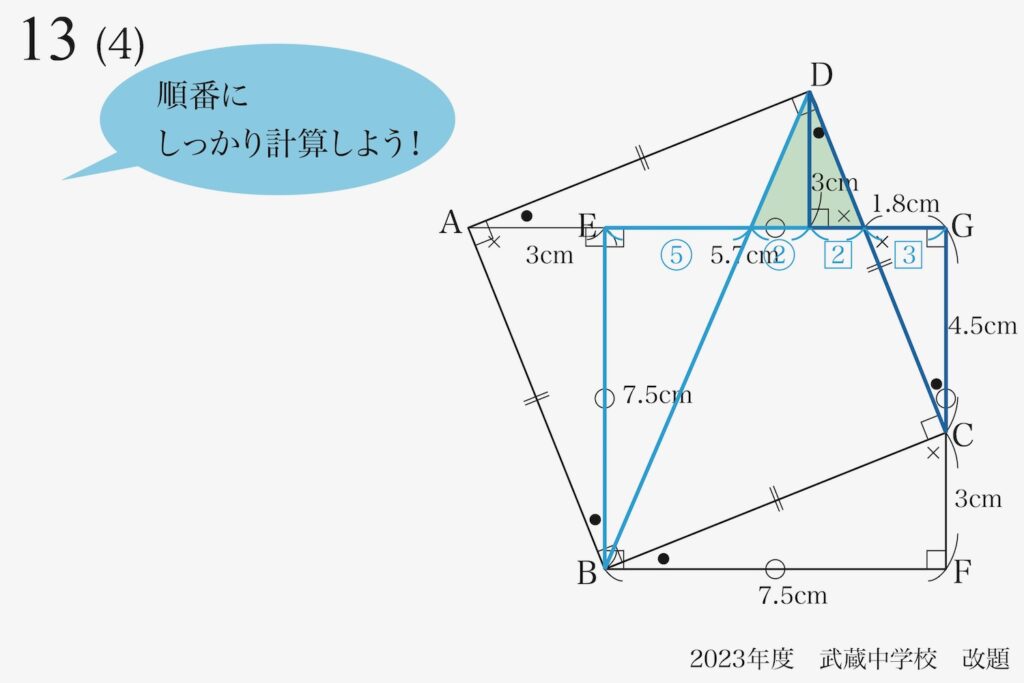
二組の相似形があり、まずは「どちらの相似形に着目するか」が大事です。

共に「相対する辺の長さ」が分かり、辺の比が分かります。

直角三角形の場合、斜辺の長さは分からないことが多いです。

そこで、「直角を挟む二辺の長さ」に着目しましょう。

今、考えている「2組の相似形」を比較します。

「分かっていること」が多い「青色の相似形」を先に考えてみましょう。

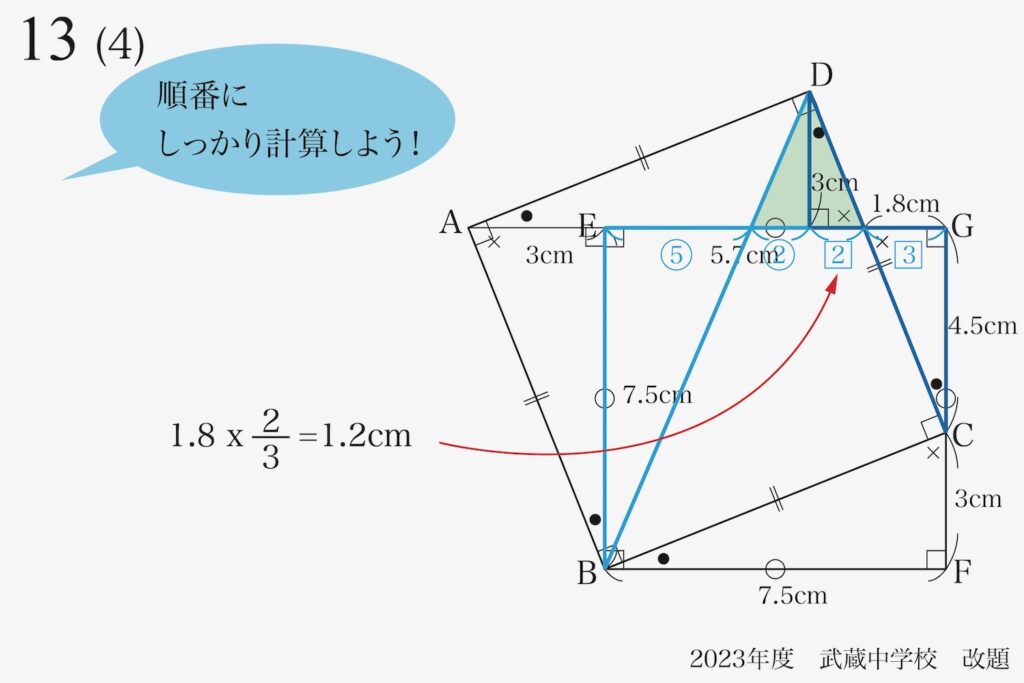
これで、「右側の相似形の組」から、辺の長さ=1.2cmが計算できました。

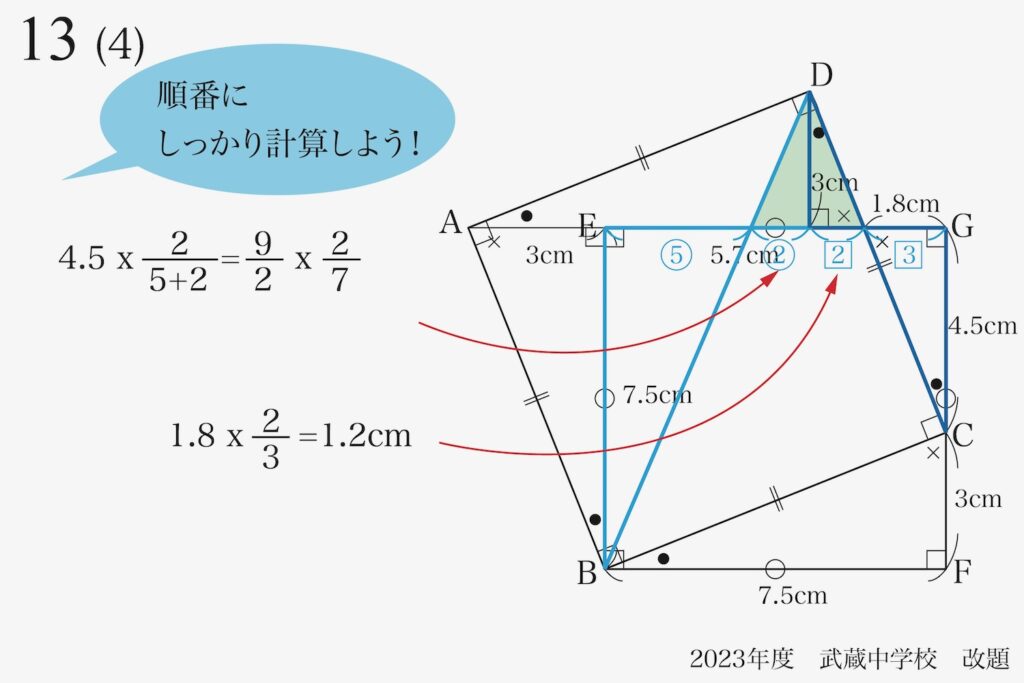
すると、「右側の相似形の組」の「対応する辺の長さの合計=5.7-1.2=4.5cm」が分かります。

対応する辺の長さは、「片方か合計が分かる」ことが大事です。

これで計算できますが、小数点の計算と分数の計算です。

こういう時は、「両方分数に直して」計算するようにしましょう。

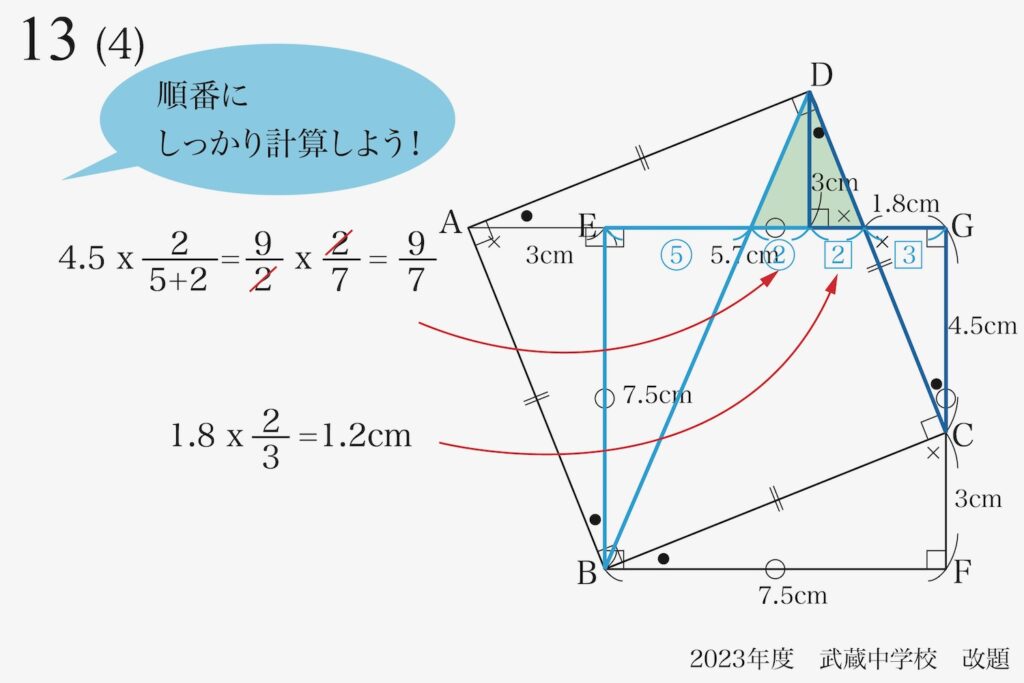
ここで、先ほど「相似形（同じ）かな？」と思った二つの三角形。

これらの三角形は「相似形ではない」ことが分かりました。

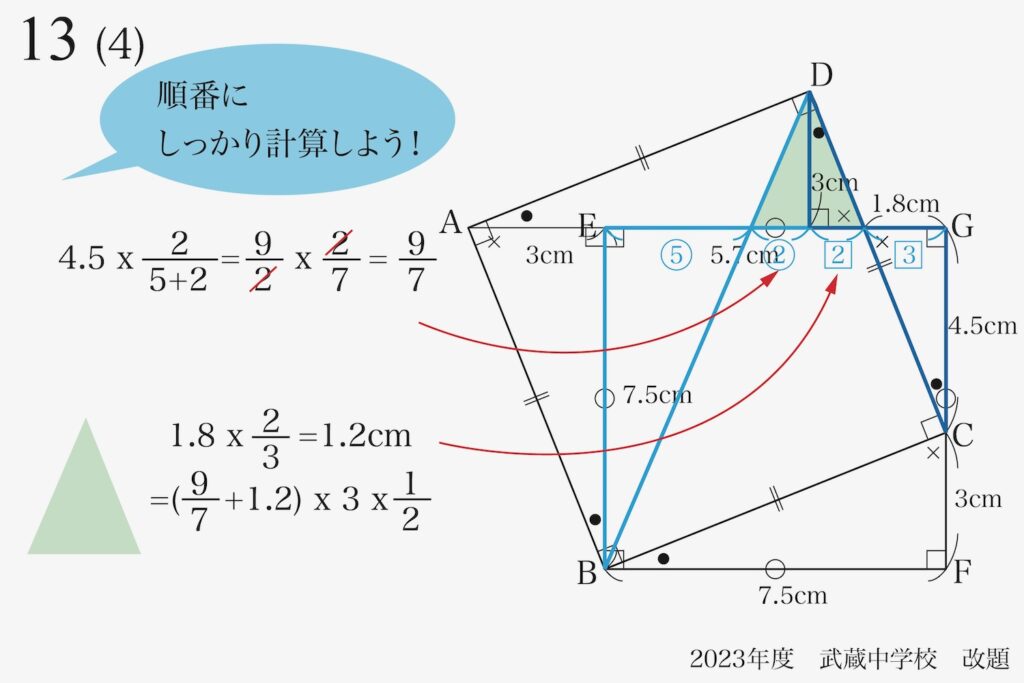
ここからは計算するだけですが、しっかりやりましょう。

こういう計算を、問題集の解答などで見て、

計算などは「飛ばさないで手を動かしてやる」ことが大事です。

計算だけでも、手を動かして実際にやってみましょう。

そういう姿勢が、「計算だけではなく、問題全体を理解する」姿勢につながります。

次回は下記リンクです。