前回は「算数的に「説明する」ことのコツ・ポイント〜特徴や性質を考える大事さ・点が「一直線上にある」こと・「〜であること」→「〜でなかったら」と考える・問題 13(3)解法〜」の話でした。
問題 13
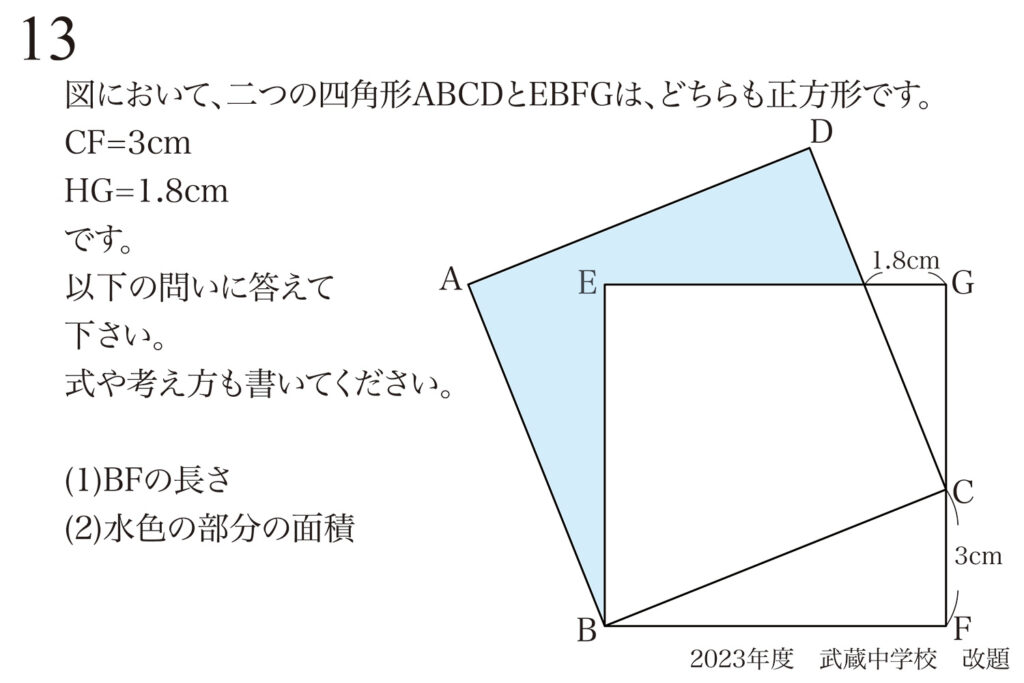
図形を算数的に考えるコツ・ポイント
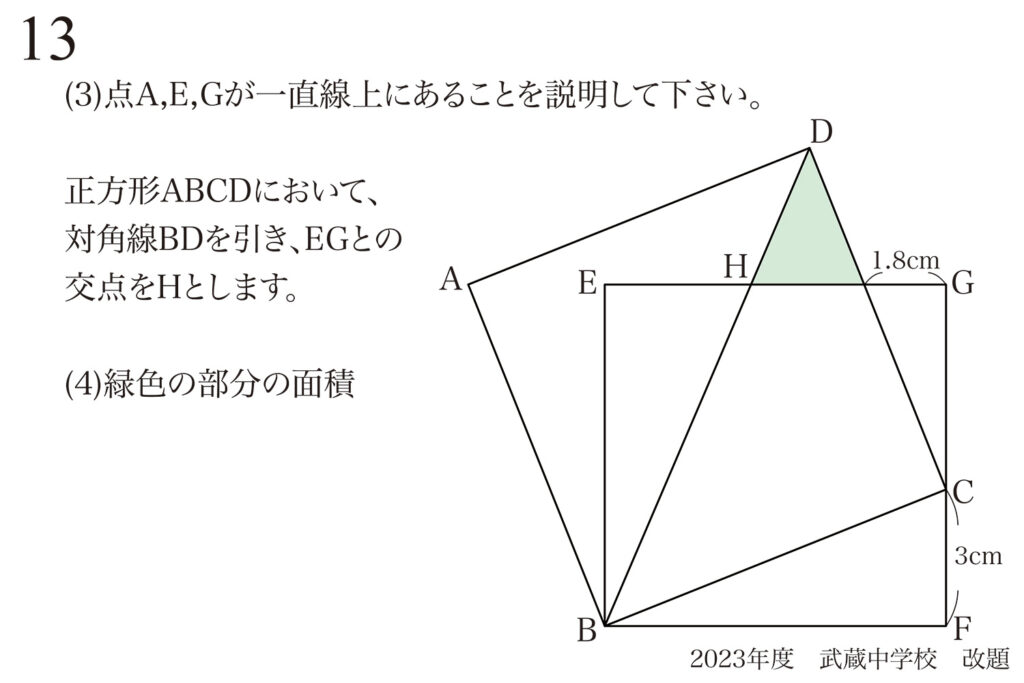
「三点が一直線上にある」ことを説明する問題です。
男子小学生「一直線上にある」のを説明って、
どうするの？
・「あること・性質」は具体的にどういうことか、を考える
・何らかの根拠を明らかにして説明
「三点が一直線にある」ことが不明瞭だと、説明するのが難しそうです。
・ある性質や特徴があることは、何らかの共通するポイントがある
・ある性質や特徴を理解する時、「〜でなかったら」を考える
「説明する」ためには、その「共通するポイント」を理解している必要があります。
そこで、「三点が一直線にある」こともう一度考えてみましょう。
女子小学生でも、「一直線上」って、
「直線の上にある」くらいしか思いつかないけど・・・
女子小学生「三つの点が全て直線の上にある」って
簡単だけど、算数で説明するのは難しいね・・・
この状況を考えるために、「三点が一直線上にない」状況を考えてみましょう。
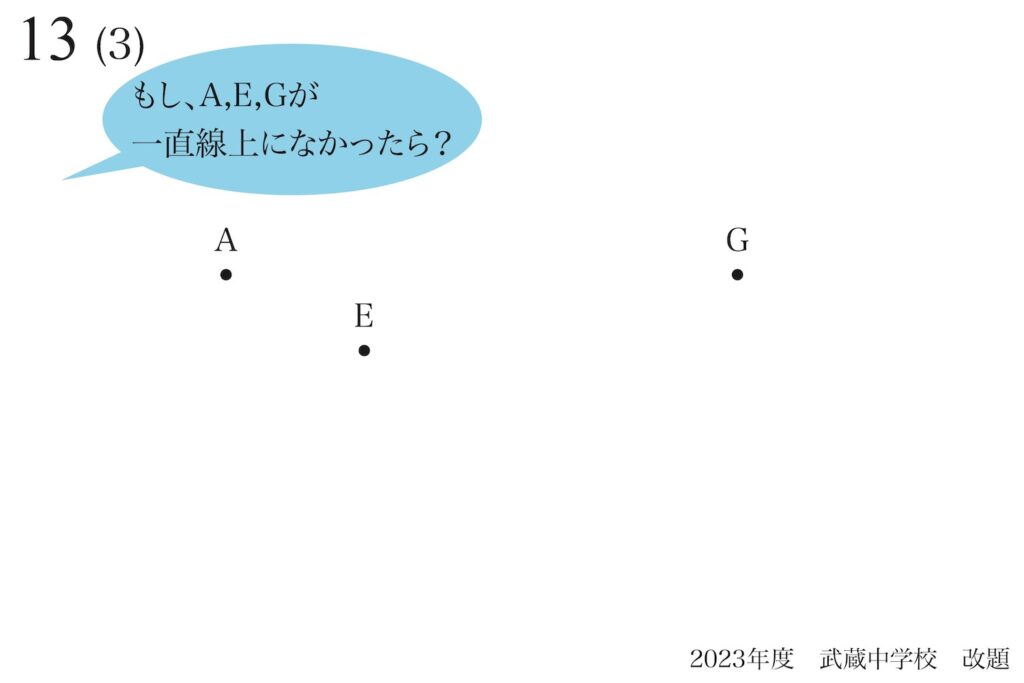
男子小学生全然
違うね。
そして、「違う状況」を考えるときは「ちょっと違う」ではなく「全然違う」状況を考えるのがポイントです。
その方が、「違う状況」がハッキリ理解できます。
具体的に「何が違う」かを図形的に考えてみましょう。
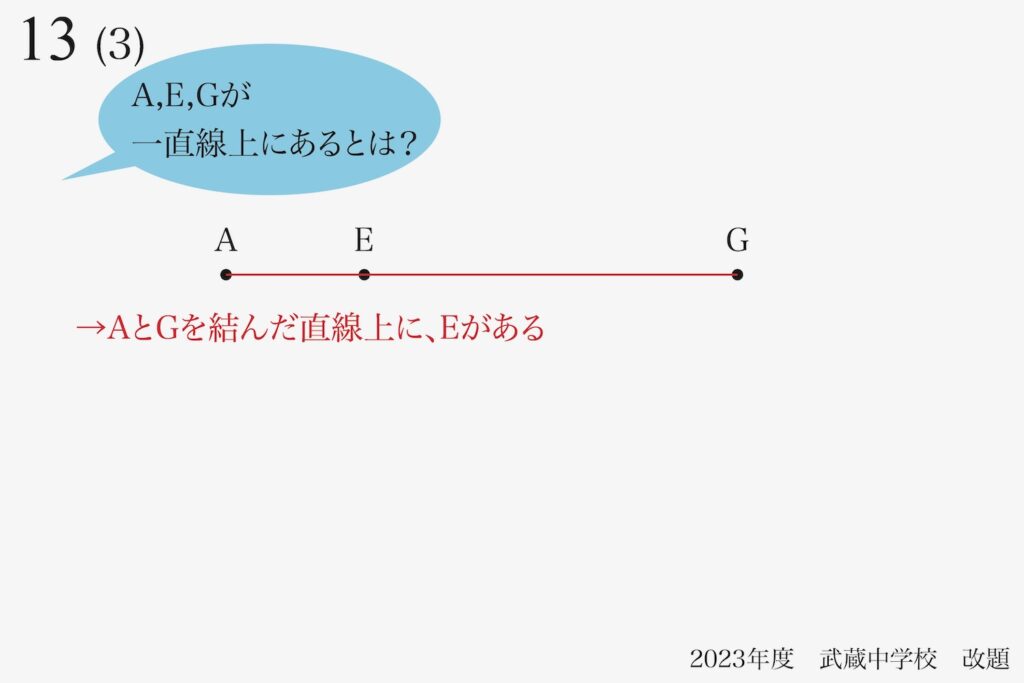
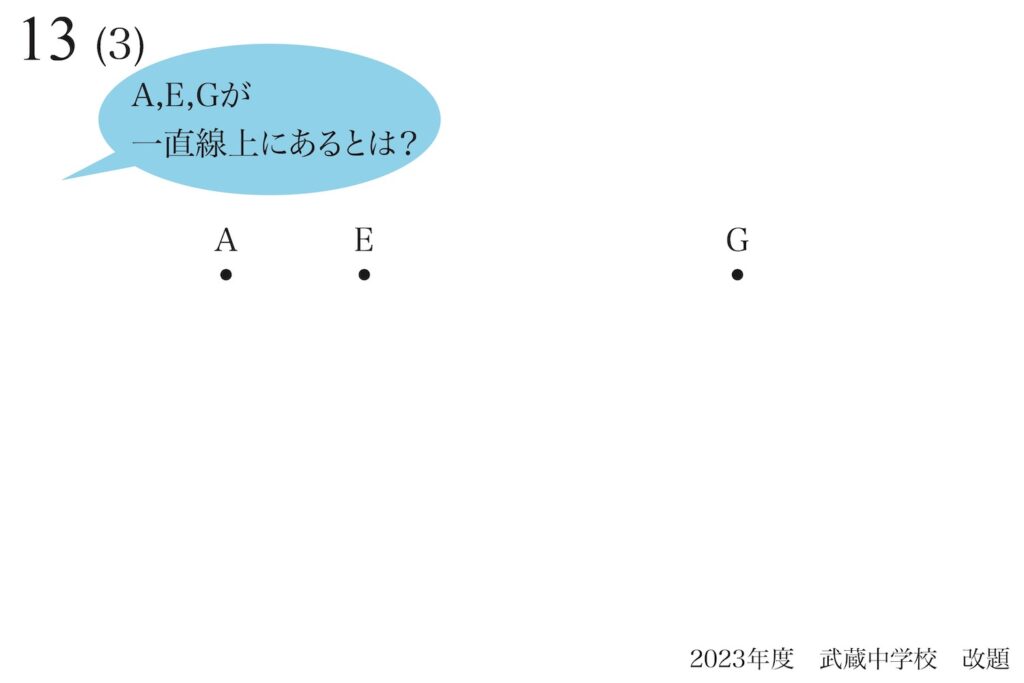
三点A,E,Gが「一直線上にある」とは「AGを結んだ直線上に、Eがある」ことです。
女子小学生確かに改めて
考えるとそうだね！
男子小学生それは
分かるよ。
これ以外に、三点A,E,Gが「一直線上にある」状況が説明できるでしょうか。
男子小学生別に、一つあれば
良いんじゃないの？
「何かの事・性質」などを説明するときに、「一通りで説明できれば良い」場合も多いです。
「説明できない」よりも「一通りでも、できる」方が遥かに良い事でしょう。
一方で、物事は必ずしも「一通りで説明」あるいは「一通りで捉えられる」ことでもないでしょう。
ある事を考えるとき、「違う説明を試みる」をやってみましょう。
それは、算数（数学）・理科などの勉強には大変役立つと思います。
そして、「記述問題への対策」にもなるでしょう。
「記述問題が難しい」方は、模範解答を「一例として書き写す」練習も大事です。
そのとき、
女子小学生少し、
説明の仕方を変えてみよう・・・
少し文章の流れや構成を、変えてみるのも良いでしょう。
あるいは、「自分が考えたこと」を書いてみるのも大事です。
ほんの少しでも良いので「異なる視点から考える」姿勢を身につけると良いでしょう。
「〜ではない」状況を具体的に考える
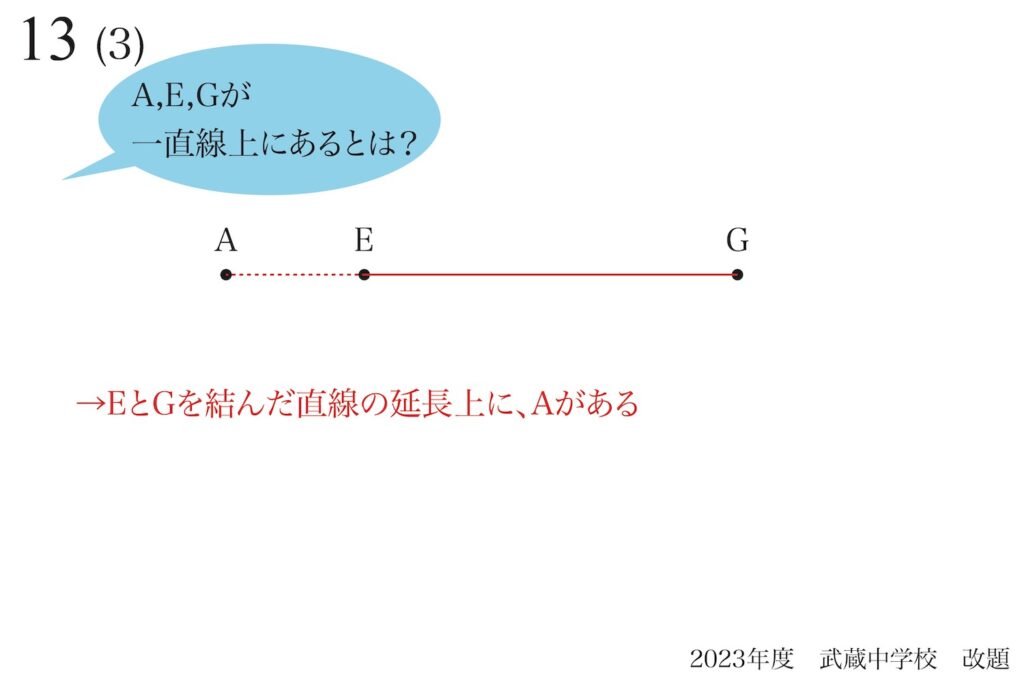
「三点A,E,Gが一直線上」は、「EとGを結んだ直線の延長上にAがある」とも言えます。
同様に、「AとEを結んだ直線の延長上に Gがある」など他の言い方も出来ます。
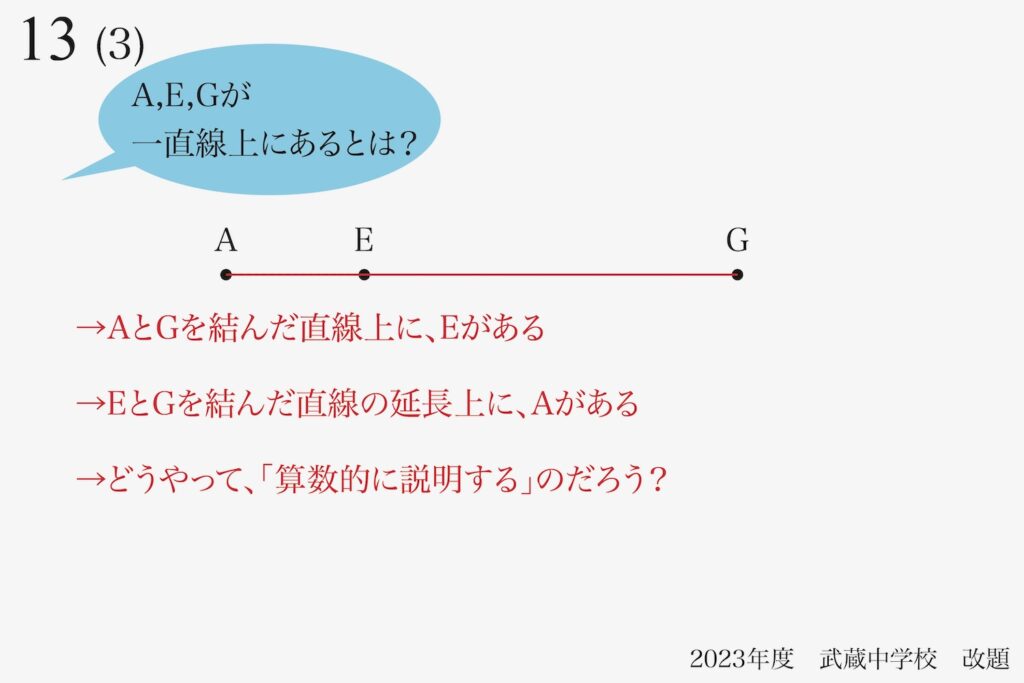
「三点A,E,Gが一直線上」を二通りで表現しましたが、「算数的に説明」を考えましょう。
ここでは、間にあるEがずれていて「三点A,E,Gが一直線上ではない」ことを考えます。
男子小学生なんか、
全然違うね！
先ほどと同様に、三点を直線で結んでみましょう。
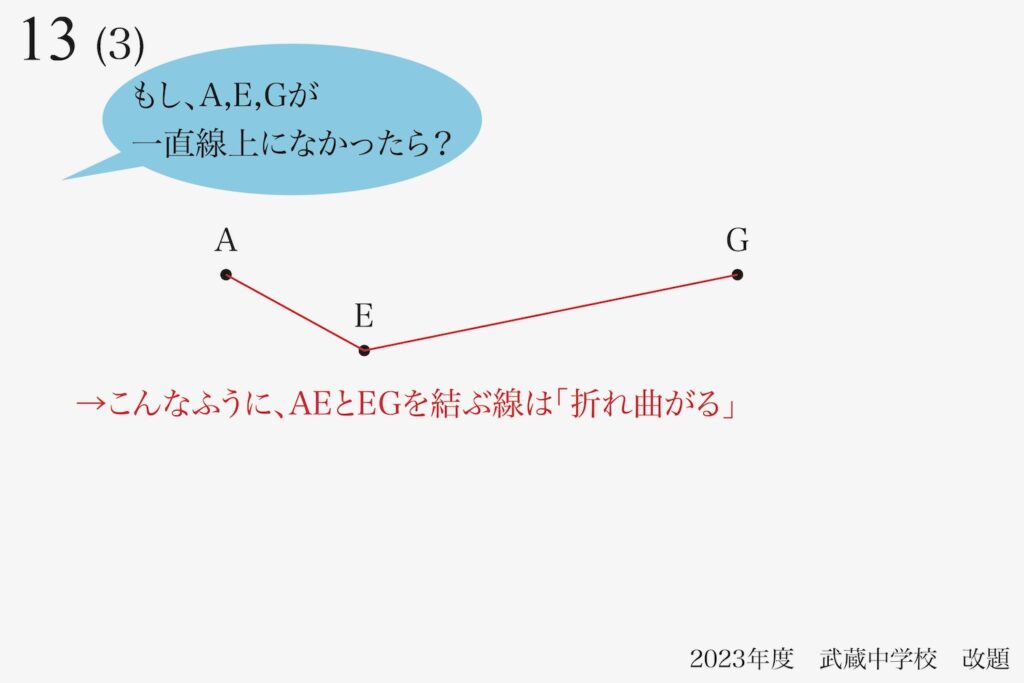
女子小学生「折れ曲がっている」
から、見るからに違う・・・
男子小学生一直線じゃないから、
全然違う。
「見るからに違う」のは大事ですが、算数なのでこの点をもう少し論理的に説明しましょう。
女子小学生論理的って
難しそうだけど・・・
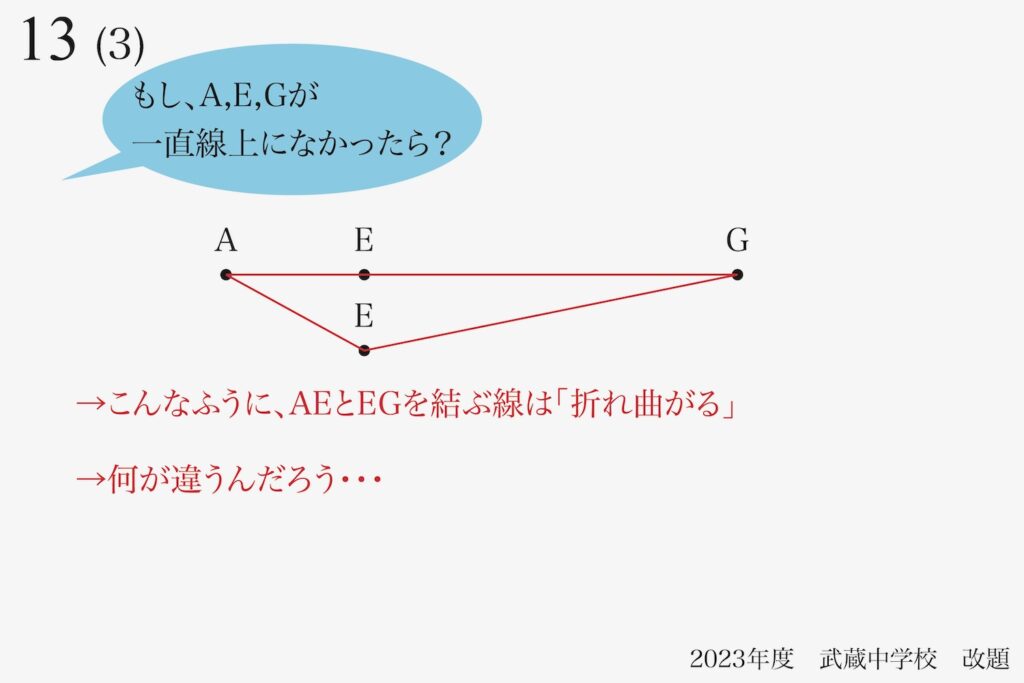
それでは、「一直線上にある」のと「一直線上にない」で、何が違うのでしょうか。
男子小学生真っ直ぐではなくて、
折れ曲がっているよね・・・
女子小学生「折れ曲がっている」では
算数的、論理的ではなさそうだね・・・
角度に注目：図形を作る辺は「長さと角度」が大事
ここで、角度に注目してみましょう。
男子小学生あっ、
角度が全然違うね！
こういうことを「頭の中でイメージする」ことも大事です。
それも大事ですが、ノートでも紙でも良いので、どんどん描いてみましょう。
「考えても分からない」ことが「描くとすぐにわかる」ことも多いです。
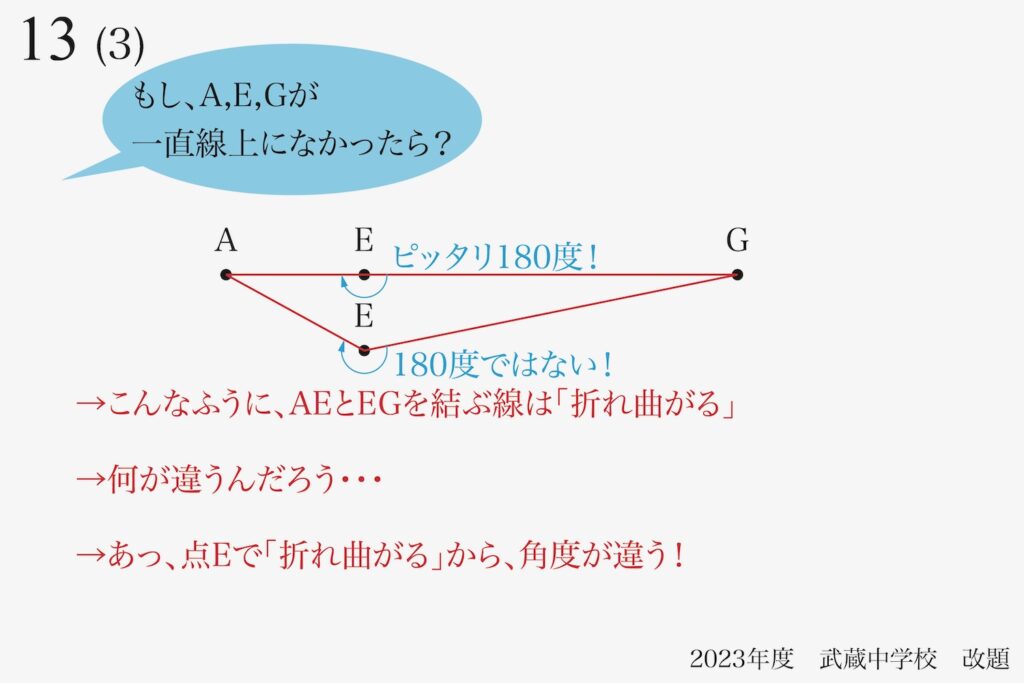
ここでは、「折れ曲がる」と「角度が違う」ことに気づきます。
「三点A,E,Gが一直線上」ならば、角AEGが180度となります。
一方で、「三点A,E,Gが一直線上でない」ならば、角AEGが180度以外の角度になります。
男子小学生うん。
これは分かるよ！
女子小学生改めて考えると
「当たり前」だけど・・・
実は「当たり前のこと」は図形だけでなく、算数では大事な場合が多いです。
長さ・面積などを考えることが多い、図形問題。
図形を構成するのは辺です。
今回考えている正方形は「四つの同じ長さの辺」が平行、あるいは直角につながっています。
・辺は「長さと角度」で決まる
・それらの辺が「どのようにつながっているか」を考える
角度は「相似形などを考える」時に考えることが多いですが、「長さ主体」になりがちです。
「角度に注目する」姿勢を身につけると、図形問題の見通しが良くなるでしょう。
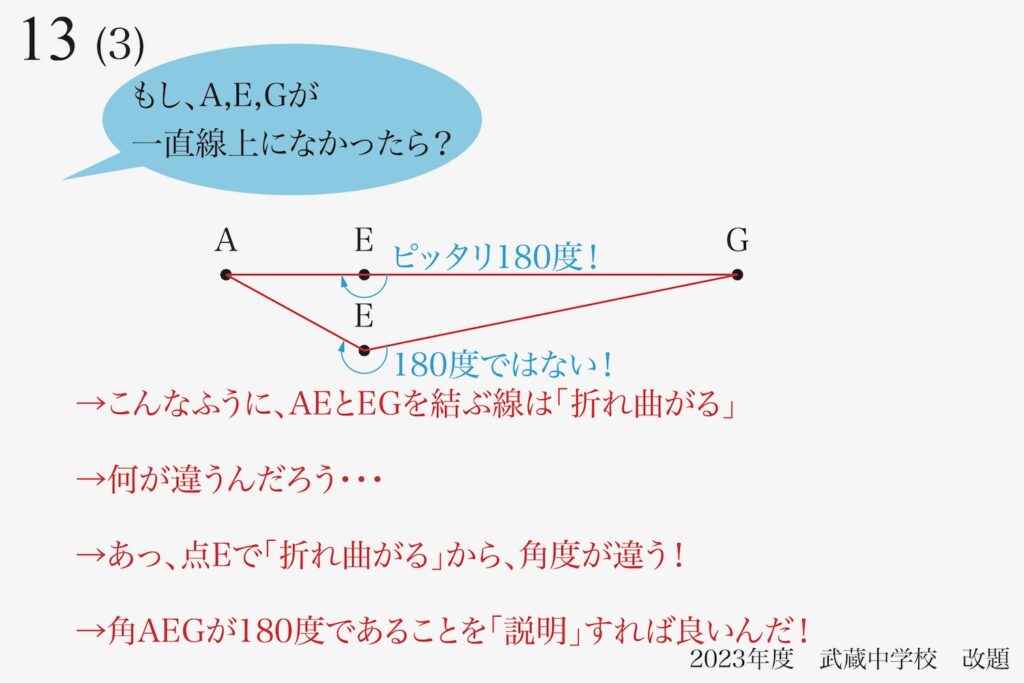
これで、「角AEG=180度」を説明すれば良いことがわかりました。
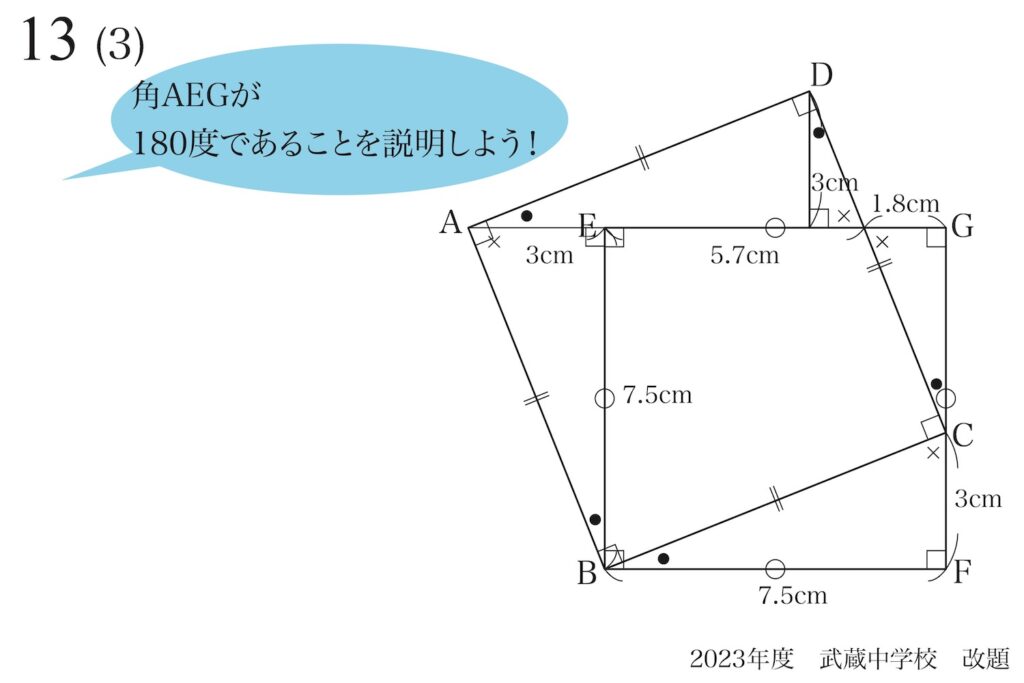
「角AEG=180度」を説明するために、これまで分かっていることを整理します。
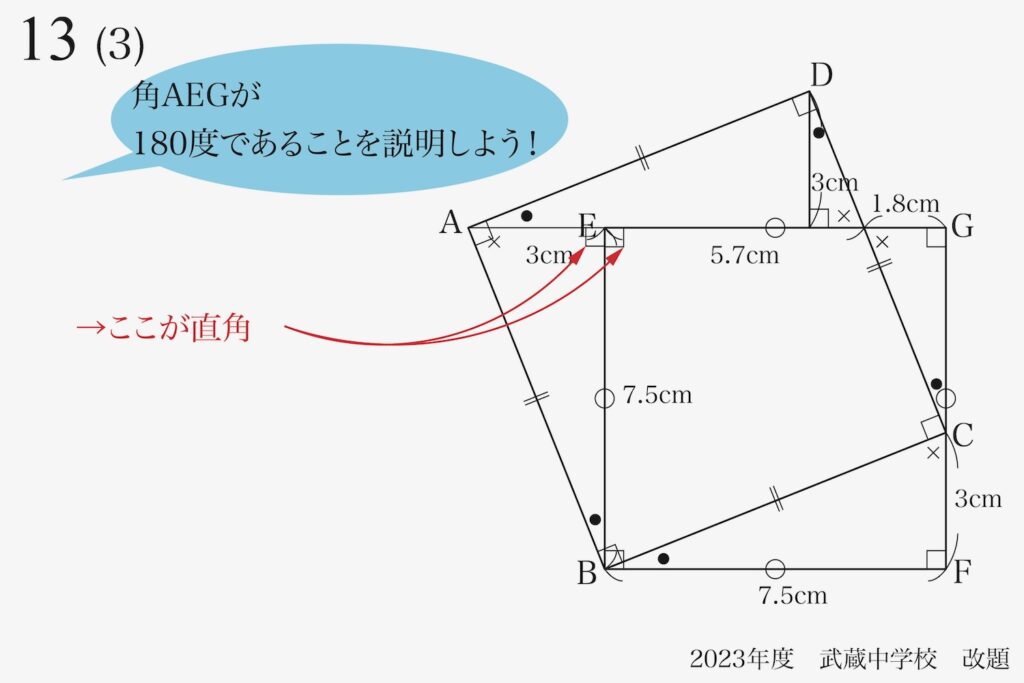
点Eの周りで、直角が二つあります。
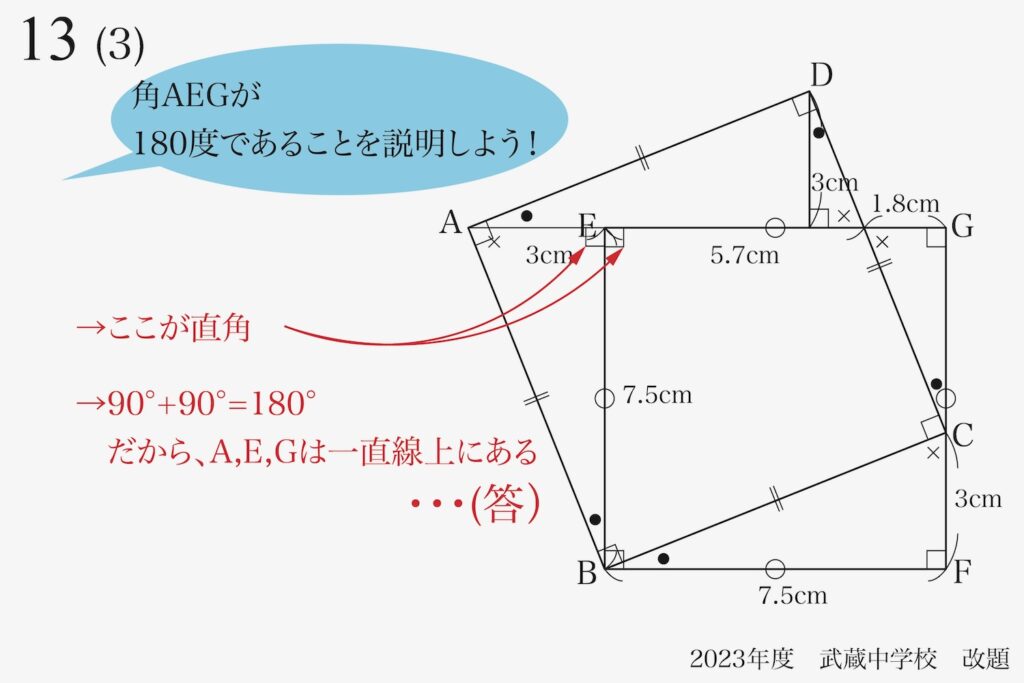
直角を二つ合わせると180度になります。
これで、「三点A,E,Gが一直線上にある」ことを説明できました。
男子小学生そういうこと
だったんだ！
女子小学生「角度に注目する」って
新鮮味があるね！
ここから、とても面白いことが分かります。
「CF=3cm」という条件がありますが、その条件と「三点A,E,Gが一直線上にある」は無関係です。
「FG上のどこにCがあっても、同じように正方形ABCDを作る」ことを考えましょう。
その時、必ず「三点A,E,Gが一直線上にある」ことになります。
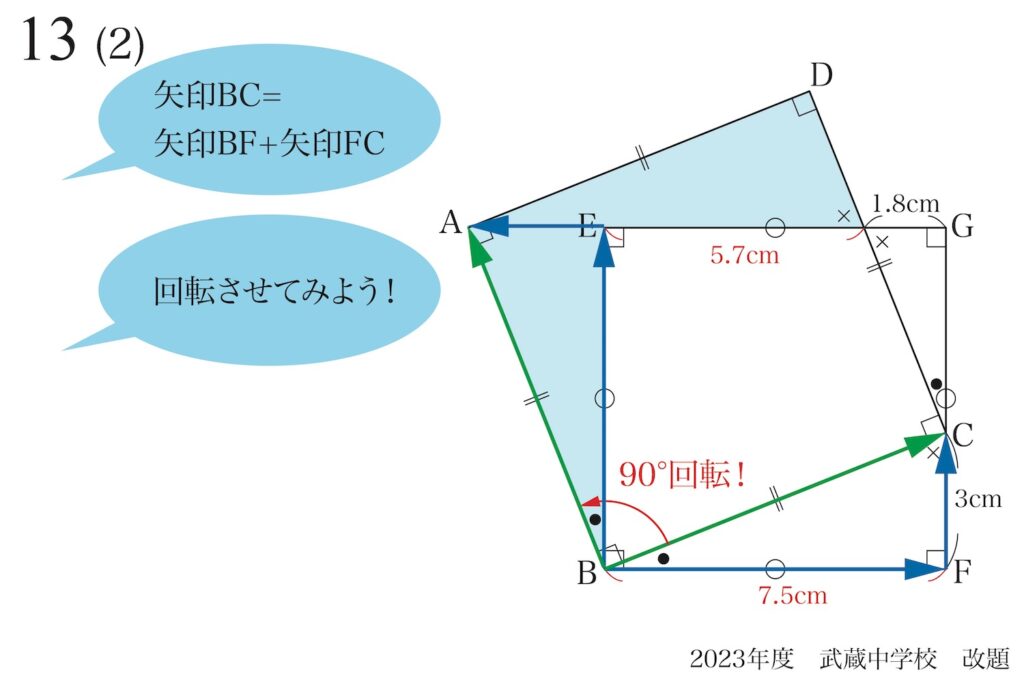
これは、以前ご紹介した「矢印」を考えても分かることです。
こういう図形の面白さを感じながら学ぶと、学力も上がるでしょう。
次回は下記リンクです。
