前回は「2つの正方形の面積計算のテクニック・コツ〜不整形な形に潜む特徴的な図形・図形の面積と辺の長さ・掛け算をまとめたり順番を変える・計算ミスを防ぐ方法・暗算を有効活用・問題 13解法(2)〜」の話でした。
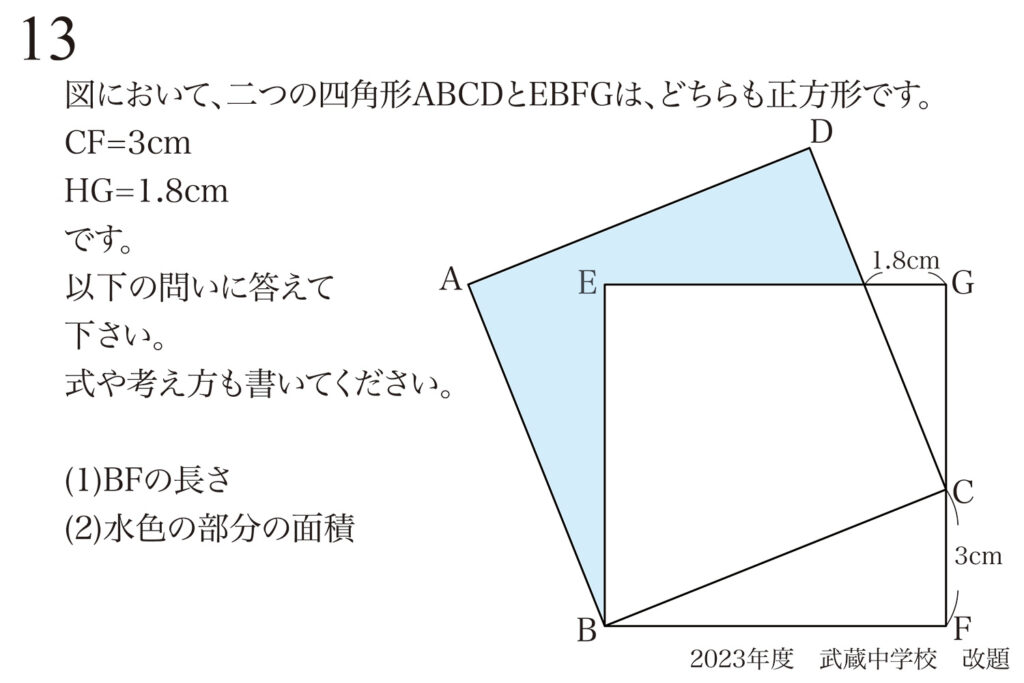
問題 13
算数的に「説明する」ことのコツ・ポイント
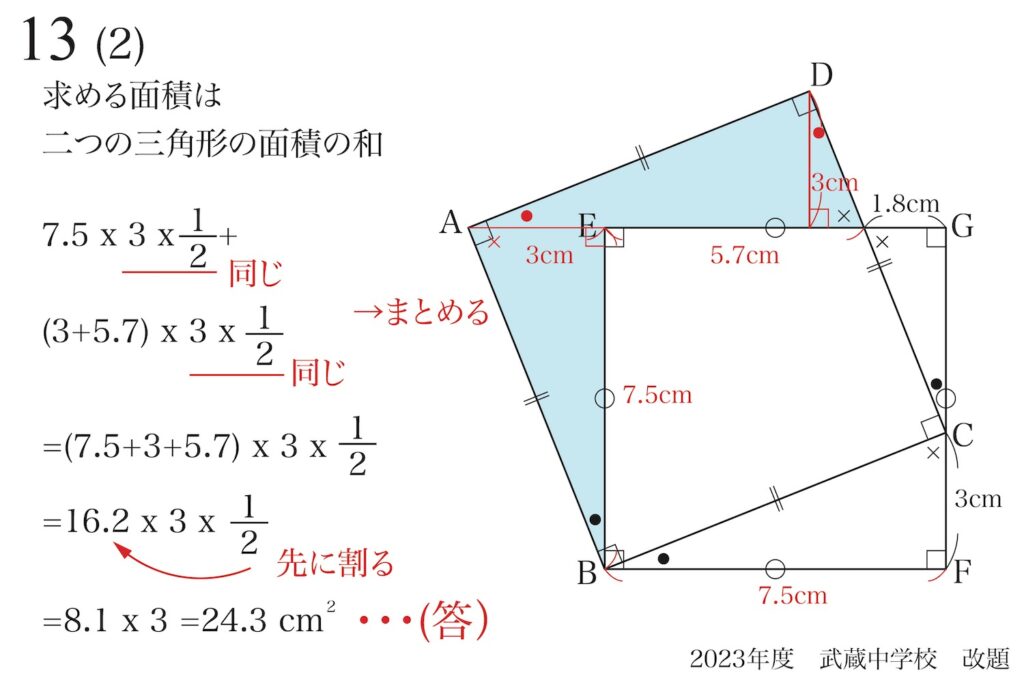
(1)(2)で長さや面積を求めました。
前回の(2)までが武蔵中のオリジナルで、(3)以降が改題した問題です。
武蔵中などの学校を合格するためには、受験生はこの問題を15分くらいで解くことが望まれます。
 男子小学生
男子小学生なんとか
なりそうかな・・・
算数・図形問題が得意な方は、もう少し短い時間で考えられる方もいるでしょう。
(4)の面積を求めるのはそれほど難問ではなく、中学受験で「よく見かける」レベルの問題です。
対して、(3)の「〜を説明してください」という出題は、あまり見かけないかもしれません。
中学校の数学以上では、「〜であることを証明しなさい」という問題が多数あります。
算数では「証明」は少しハードルが高いので、「説明」で考えてみましょう。
「必ずしも、算数(数学)的に厳密でなくても良い」ですが、ある程度の論理性は必要です。
例えば、「(算数的に)説明してください」なので、



見れば、
わかります。
あるいは、



これは、
明らかです。
このような「説明」は「算数的な説明ではない」ので✖️となります。
きちんと、算数的に、論理的・合理的に「説明する」必要があります。
説明する問題は、実験問題など理科で出題されることがあるでしょう。
社会でも「気づいたことを説明しなさい」という問題があります。
算数では「あること・性質を説明しなさい」という出題は少ないかもしれません。
ここで「算数的に説明する」ことを具体的に考えてみましょう。
・「あること・性質」は具体的にどういうことか、を考える
・何らかの根拠を明らかにして説明
特徴や性質を考える大事さ

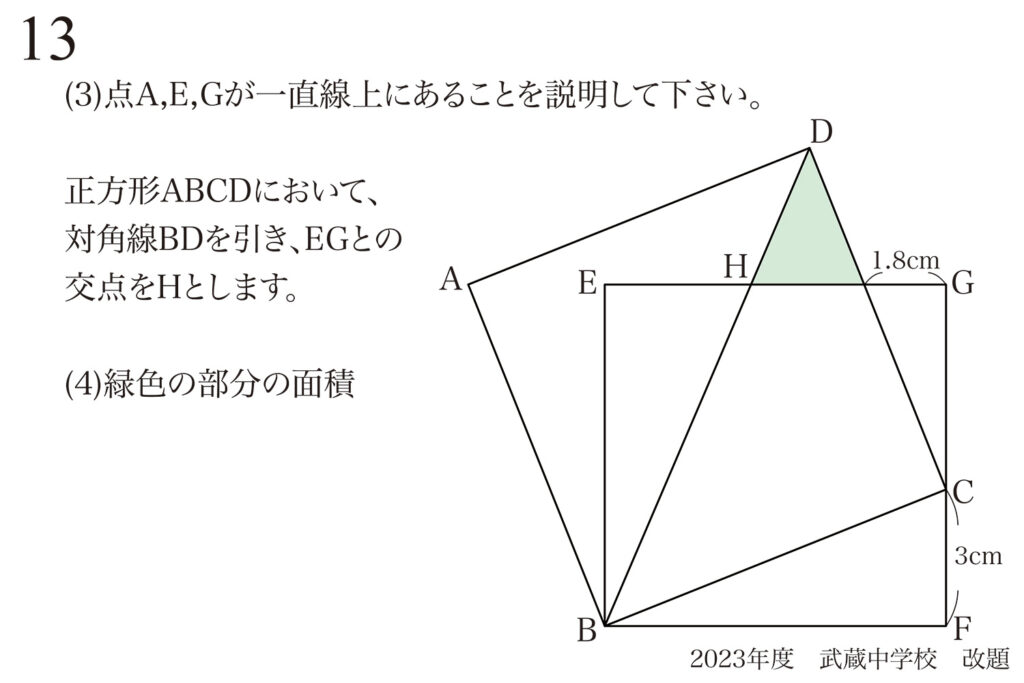
中学受験で、あまり見かけない「説明してください」を出題した理由。
それは、「図形の性質を考える大事さ」を考えてみることが、学力向上につながると考えたからです。
図形に限らず、いろいろな分野で「性質をしっかり考える・理解する」ことは大事です。
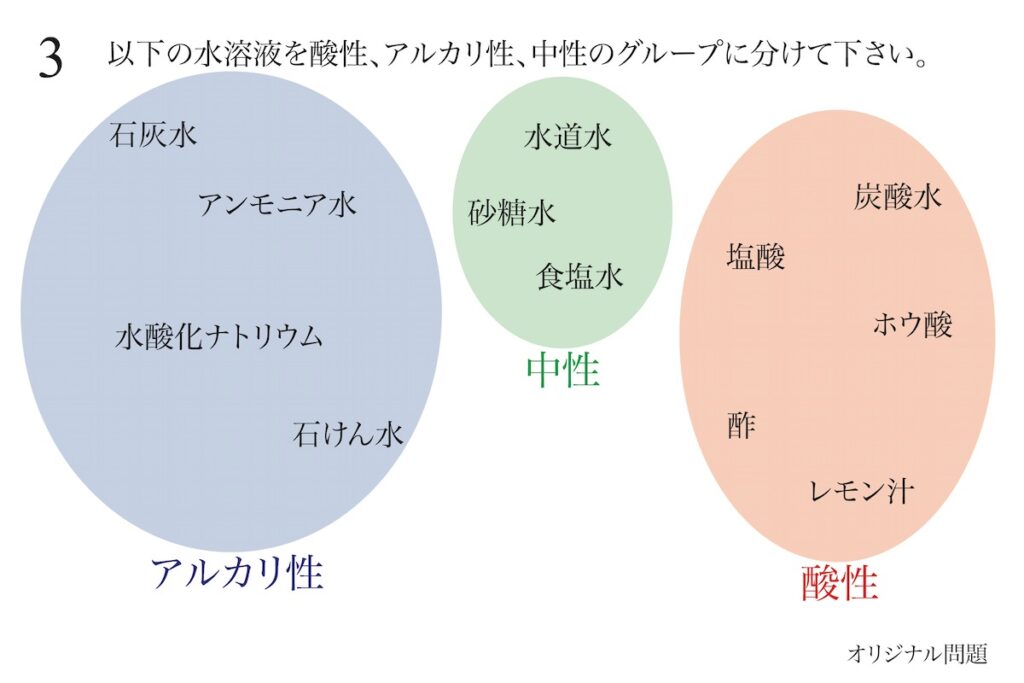
水溶液の性質をイメージする話を、上記リンクでご紹介しています。
「性質」は理科の水溶液の性質、中学以上の化学の元素の性質などを思い浮かべるかもしれません。
例えば、水溶液では「酸性」「アルカリ性」「中性」があり、それらを「丸暗記する」こともあります。
英単語などは「丸暗記」することも多いです。
一方、こういう「性質に関すること」を「丸暗記だけ」は避けた方が良いでしょう。


「性質」は、「何らかの共通性があるから」性質で分かれているのです。
その「共通性」という根本的なことを考えず、「丸暗記」しても、応用力は育たないでしょう。
単に「下記水溶液から、酸性の水溶液を選びなさい」という問題なら「丸暗記」で対応できます。
本来有する「性質」を問う内容の場合、「丸暗記」では対応できないことがあるでしょう。
「酸性・アルカリ性」などのグループ分けの時は「グループ分けの理由」を理解しましょう。
点が「一直線上にある」こと
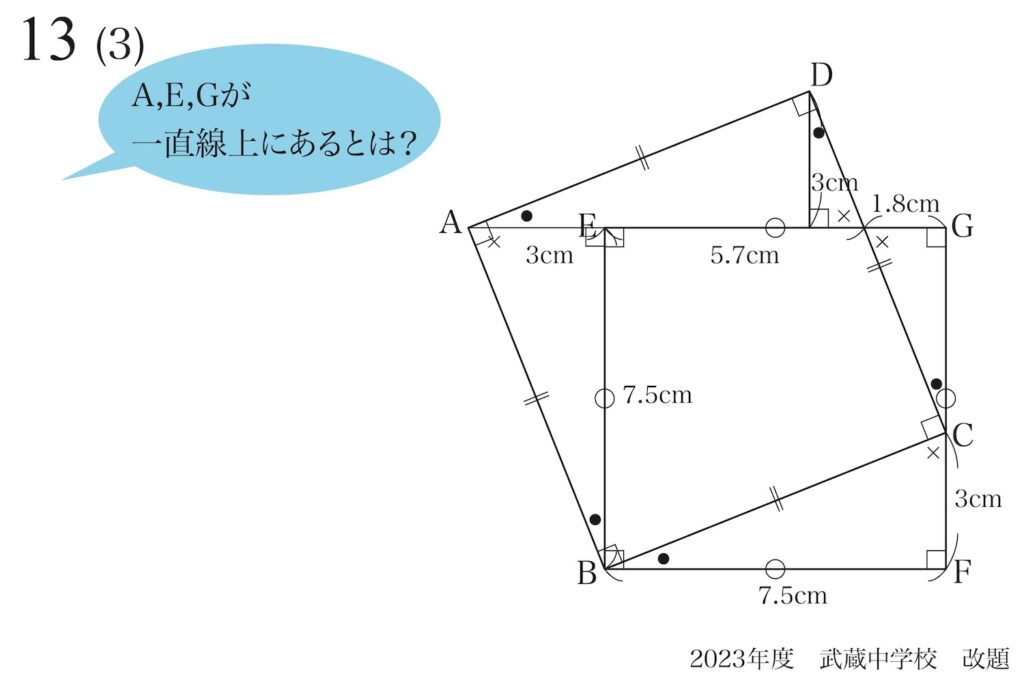

実際に「点が一直線上にある」ことを考えてみましょう。
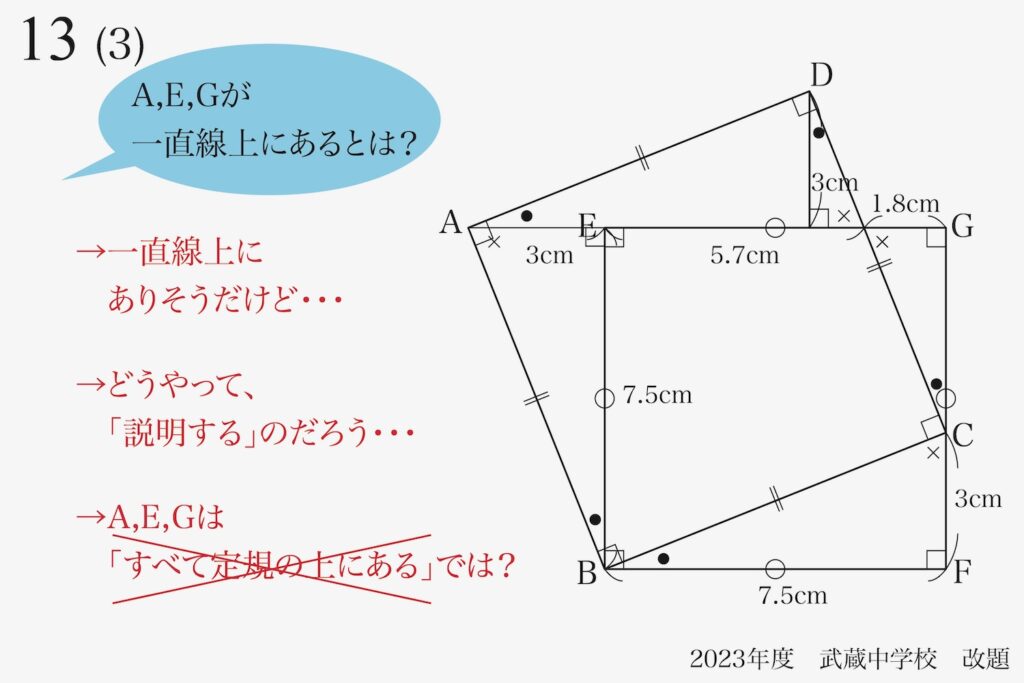
現在、(2)まで解いて分かっていること(長さ・角度)を図形に描きこんでみます。
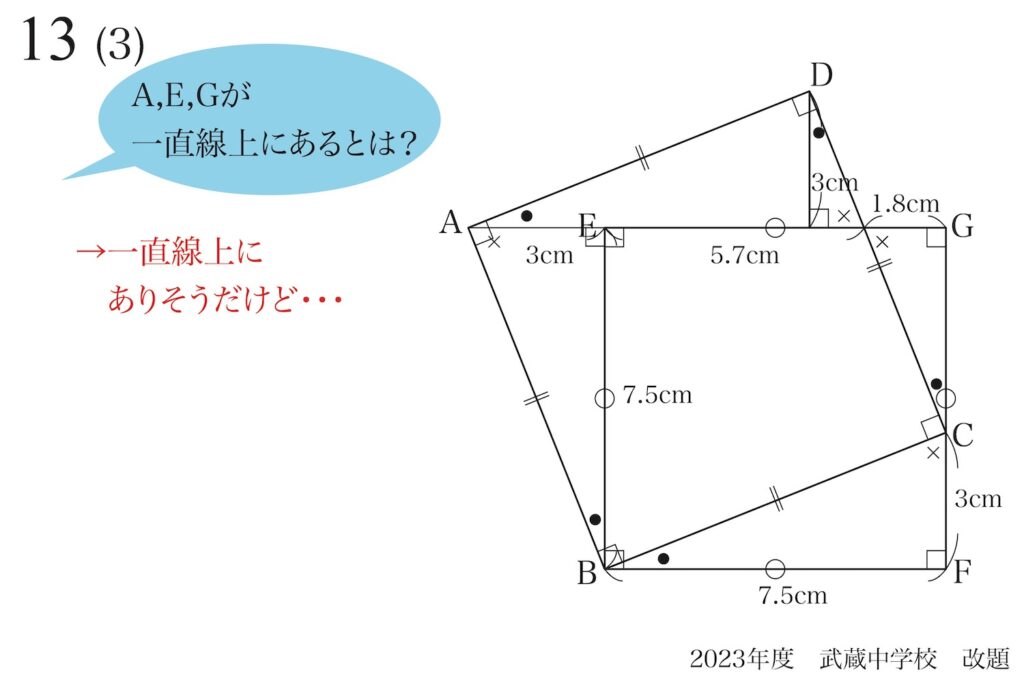

いかにも「A,E,Gは一直線上にありそう」な感じがします。
ただし、「感じがする」では、「算数的な論理性」がありません。
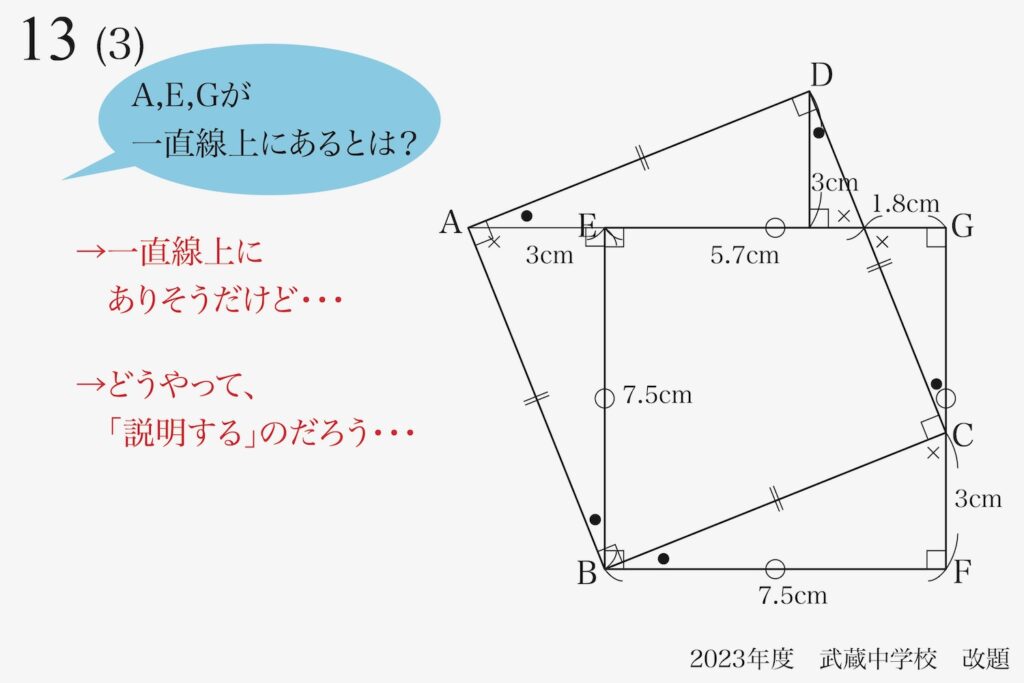

どうやって「説明する」のか、少し考えてみましょう。
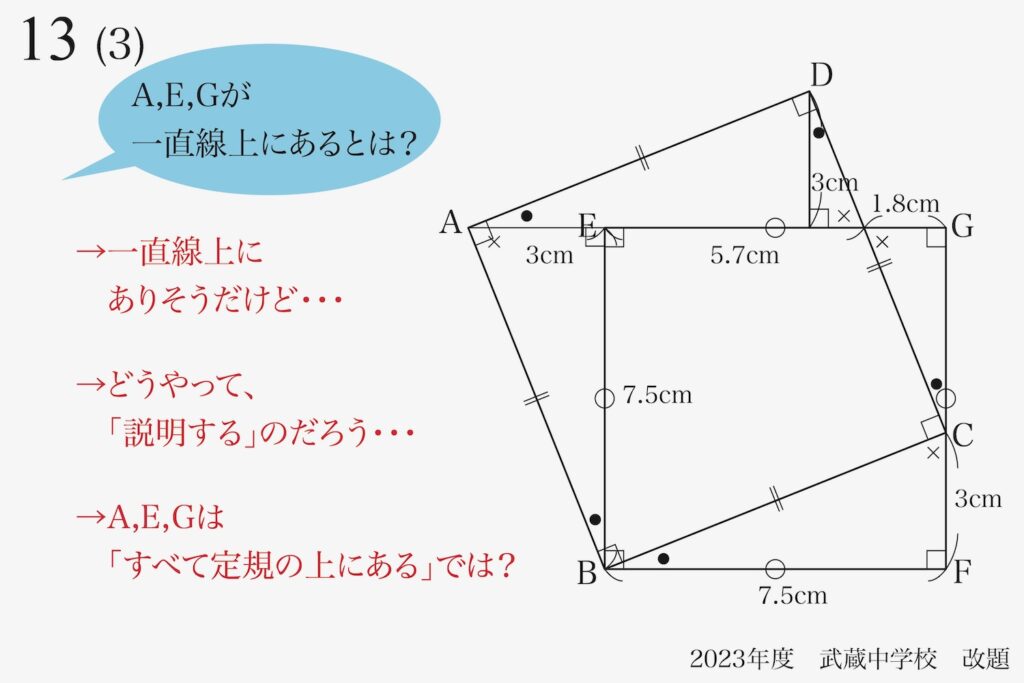

「一直線上」は、「定規で直線を引く」と「全ての点(A,E,G)がその上」ということです。



うん。
そうだよ。



全部が、
「定規の上にある」で答えかな・・・

これでは、「説明になっていない」のです。



なんで、
ダメなの?
「定規の上」「定規で描いた線の上にある」ということは「事実」でしかないのです。
「事実」を示しても必ずしも「論理的」ではないので、これでは説明にはなりません。
「〜であること」→「〜でなかったら」と考える
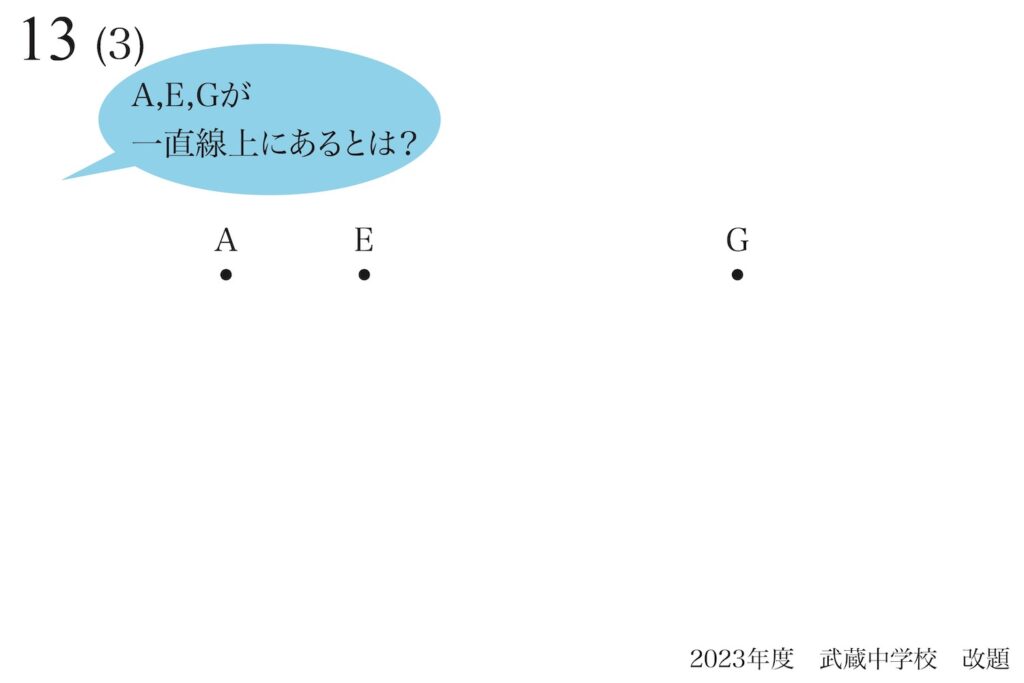




じゃ、
どうやって「説明する」の?
少し考えてみましょう。
この「一直線上」は、それほど難しいことではないですが、「説明」となるとハードルが上がります。
他の図形は消して、「三つの点A,E,Gが一直線上にある」ことを考えてみましょう。



「考える」って言ったって、
一直線上だから・・・
仮に、「三つの点A,E,Gが一直線上にない」としたら、どうなるでしょうか。



「一直線上にない」ことを
考えて、どうなるの?
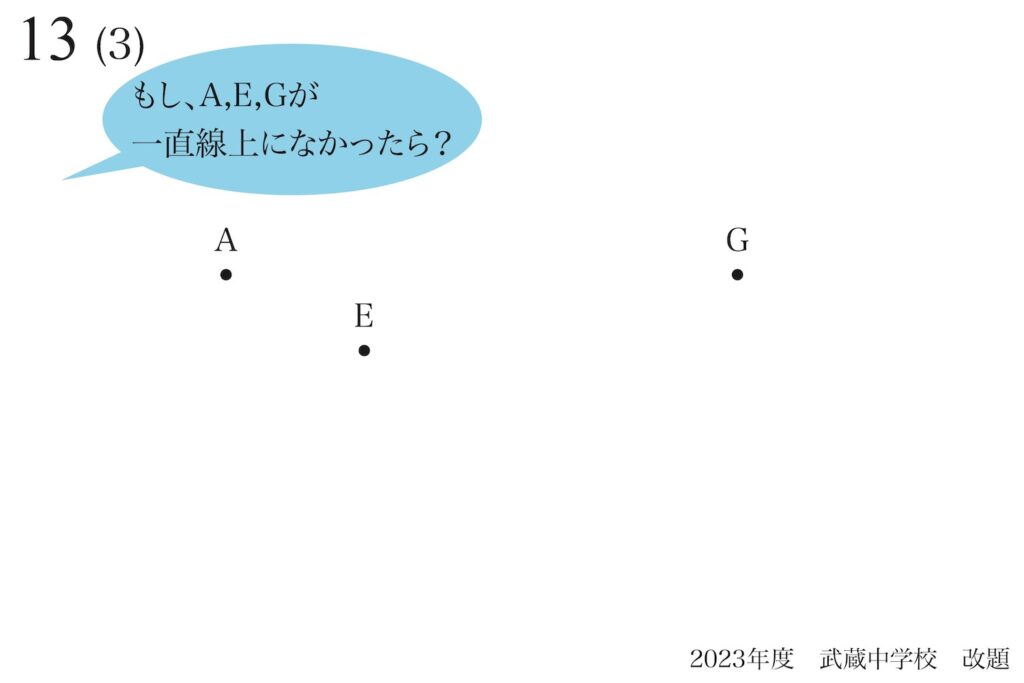

例えば、Eが「一直線上からずれている」と考えてみましょう。
このように「〜でなかったら」と考えることは、算数(数学)・理科では大事な考え方です。
・ある性質や特徴があることは、何らかの共通するポイントがある
・ある性質や特徴を理解する時、「〜でなかったら」を考える
そして、そういう「〜でない」状況は、少し大げさに考えると良いでしょう。
「三点、A,E,Gが一直線上になかったら」を少し考えてみてください。
次回は下記リンクです。



