2つの正方形の面積計算のテクニック・コツ〜不整形な形に潜む特徴的な図形・図形の面積と辺の長さ・掛け算をまとめたり順番を変える・計算ミスを防ぐ方法・暗算を有効活用・問題 13(2)解法〜｜中学受験・武蔵中・算数実践88

前回は「矢印で図形問題を攻略するコツ・ポイント〜自分の手で描く大事さ・水泳と勉強は同じ・矢印ごと回転・分かったことを図形に描きこむ・図形のどこに着目するか・「分かっていること」を大事に・問題 13(2)解法〜」の話でした。

問題 13

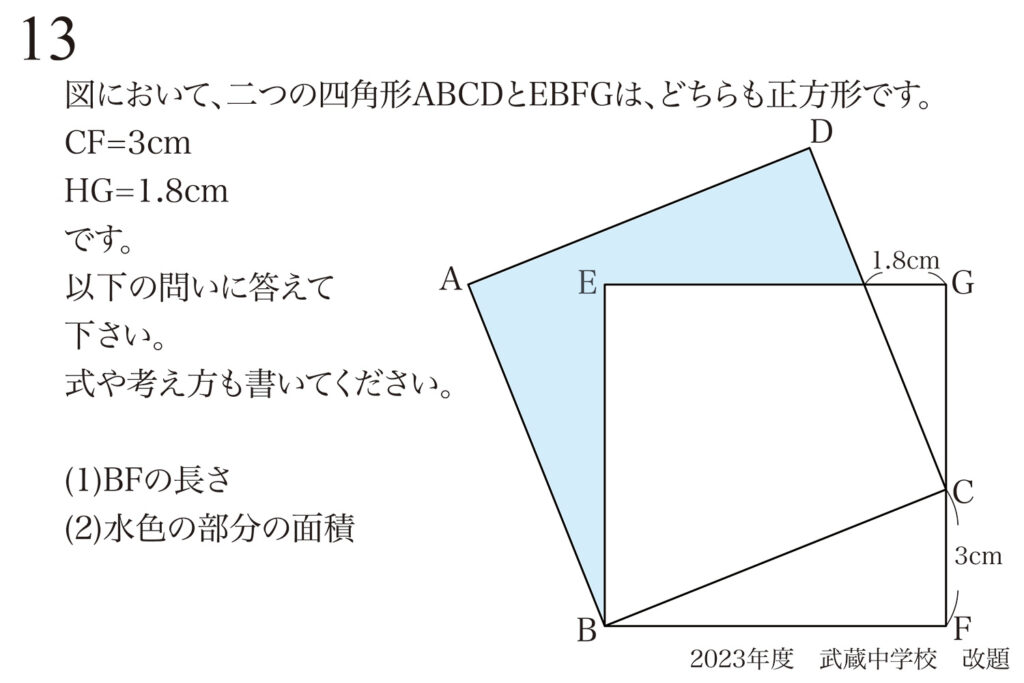
不整形な形に潜む特徴的な図形：図形の面積と辺の長さ

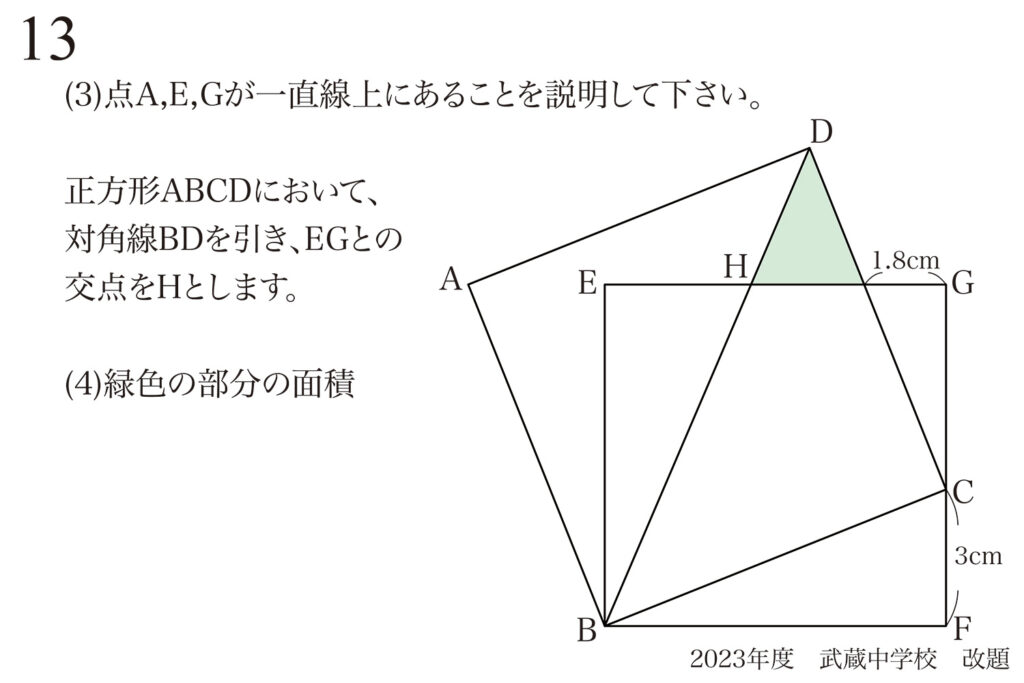
不整形な五角形の面積を求める(2)の問題。

矢印の考え方で、「不整形な五角形=直角二等辺三角形が二つ」と分かりました。

図形問題で「少し変わった形（部分）の図形」は、特徴的な図形が隠れていることが多いです。

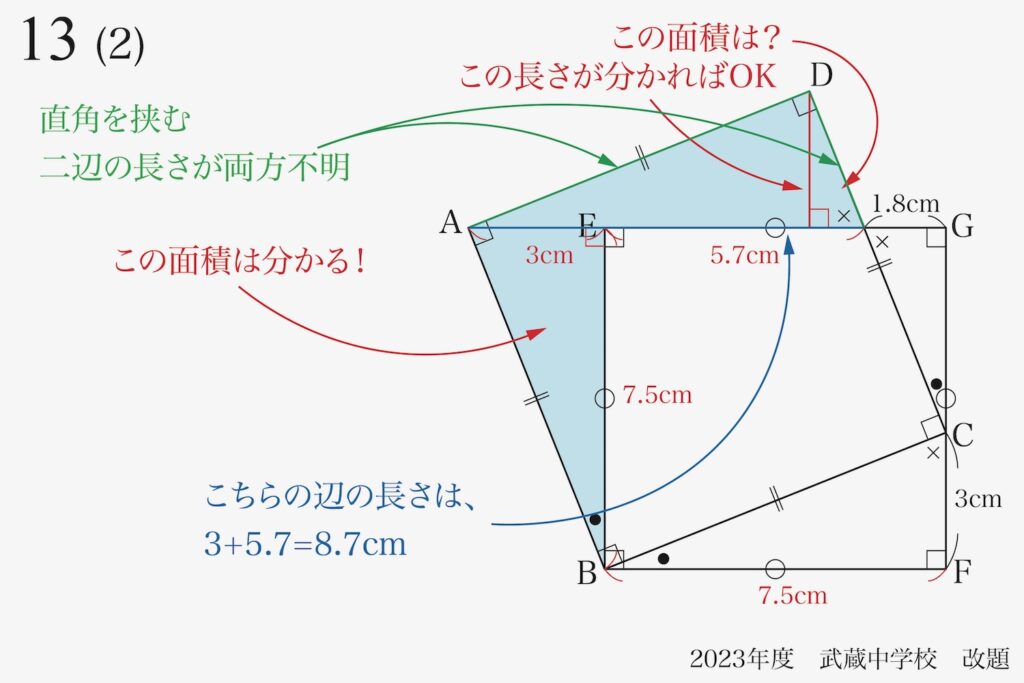
図形問題の面積を考えるとき、「どこの長さを求めようとするか」が大事です。

「直角三角形の面積」は「直角を挟む2辺の長さ」が分かると早いのです。

ここでは、ここでは両方分かりません。

そこで「分かっている斜辺の長さを利用して、面積を求めよう」と考えましょう。

「矢印」を考えたら、いくつか長さが新たにわかり、新たに「AEを結ぶ線」が登場しました。

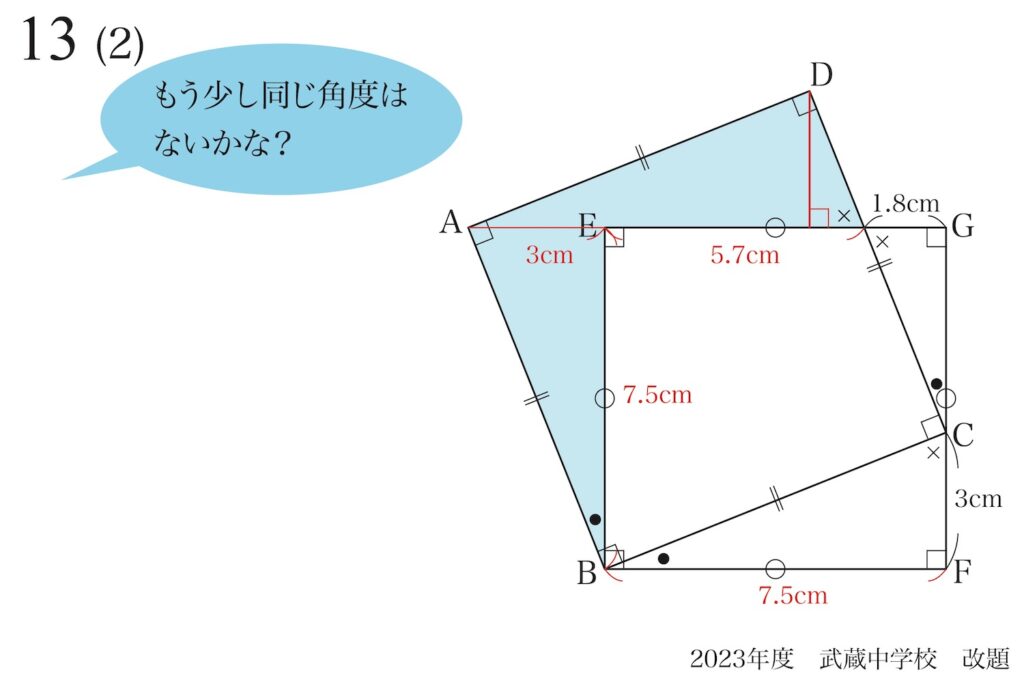
ここで、もう少し角度に注目しましょう。

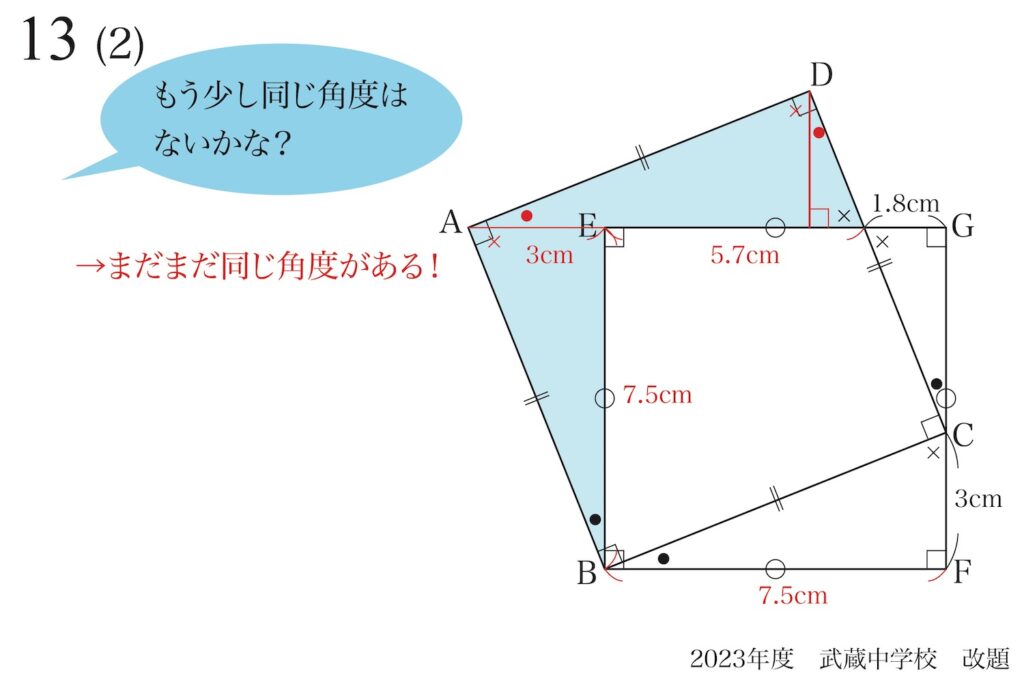
まだまだ同じ角度（赤丸）がありました。

同じ角度が見つかったら、相似形を探しましょう。

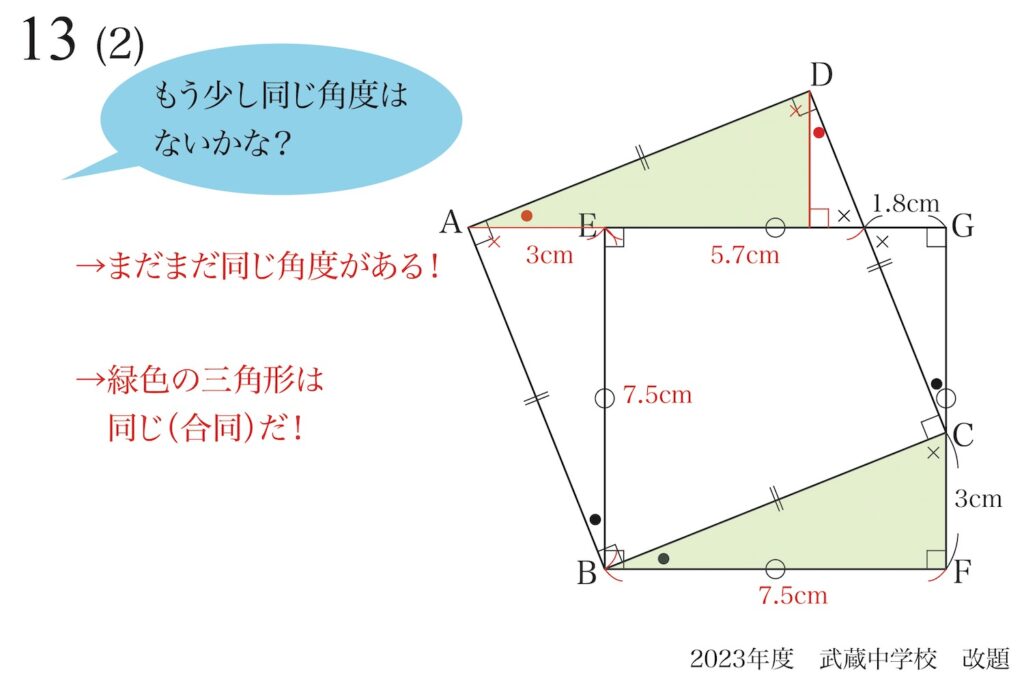
上の図で緑色の2つの三角形は同じ（合同）です。

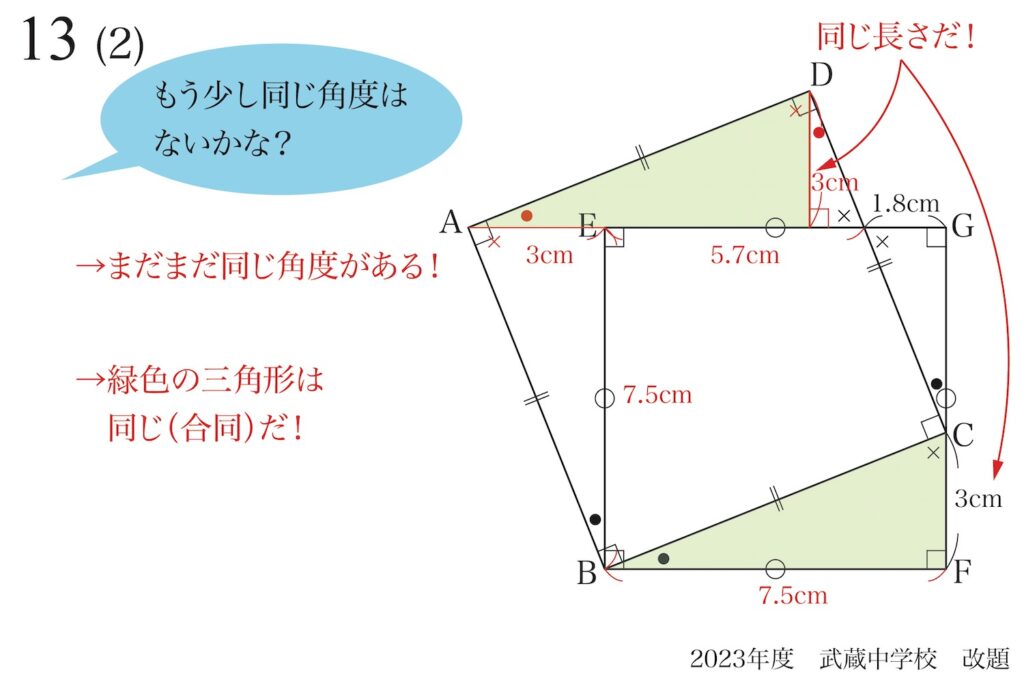
同じ（合同）図形が見つかると、同じ長さが見つかるので、見通しが良くなります。

面積計算のテクニック・コツ：掛け算をまとめたり順番を変える

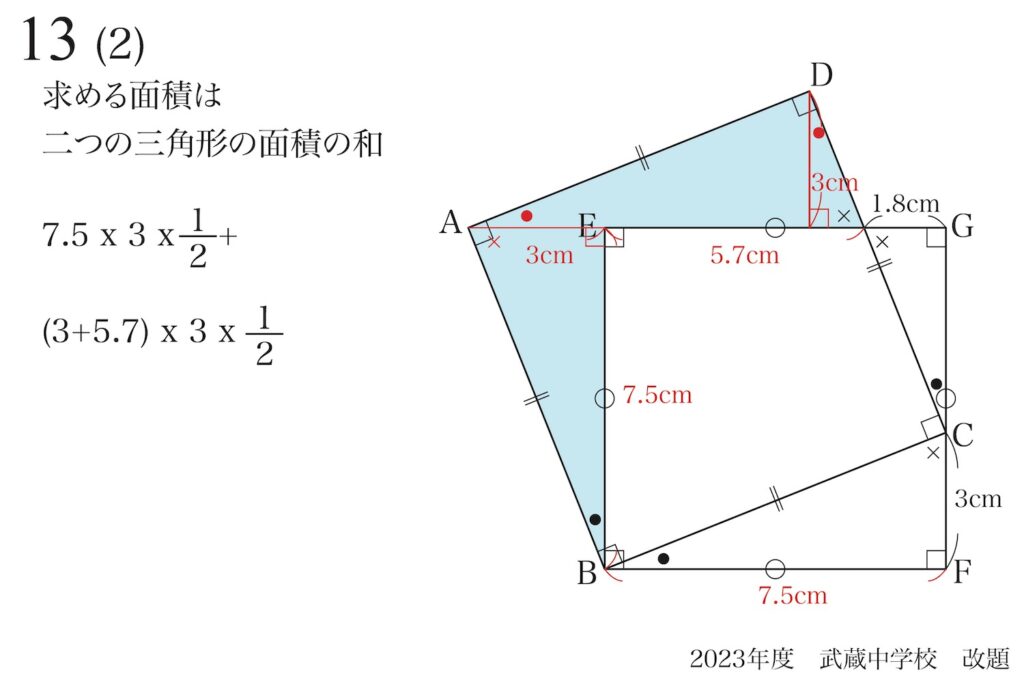
これで、問題の面積は求まりそうです。

上の式を計算すれば良いです。

ここで、少し計算のテクニック・コツの話です。

テクニック的な話は「本質的なことではない」こともありますが、「時間内に問題を解く」にはテクニックも必要です。

こういう計算をする時、ガリガリ計算を始めても良いですが、

と考えてみましょう。

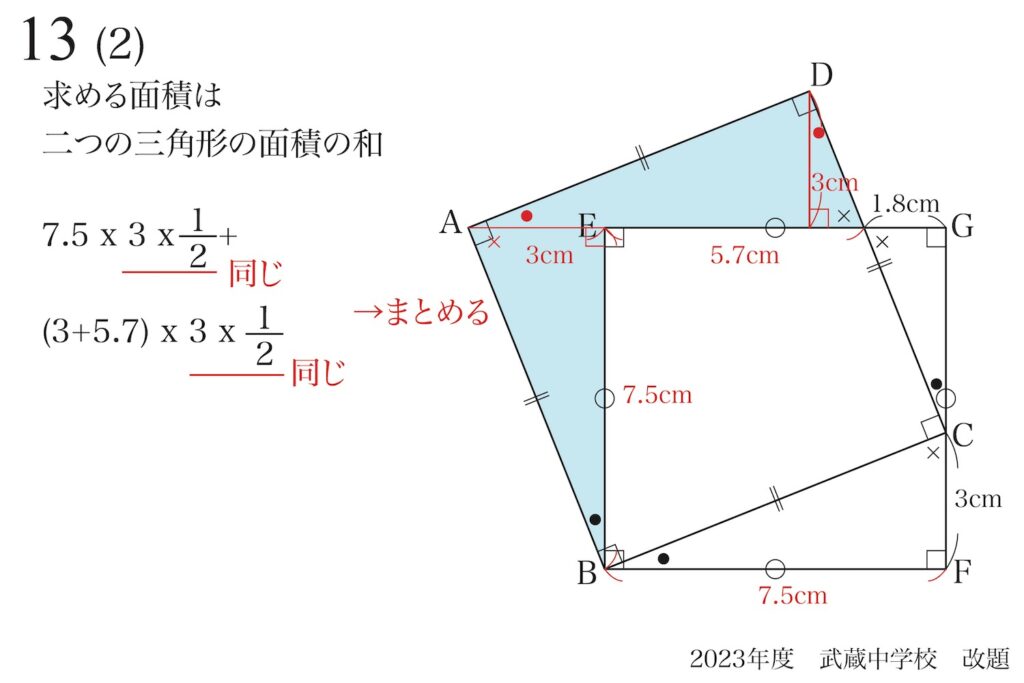
今回は、三角形の面積の「掛ける長さが同一の3cm」ですから、まとめられます。

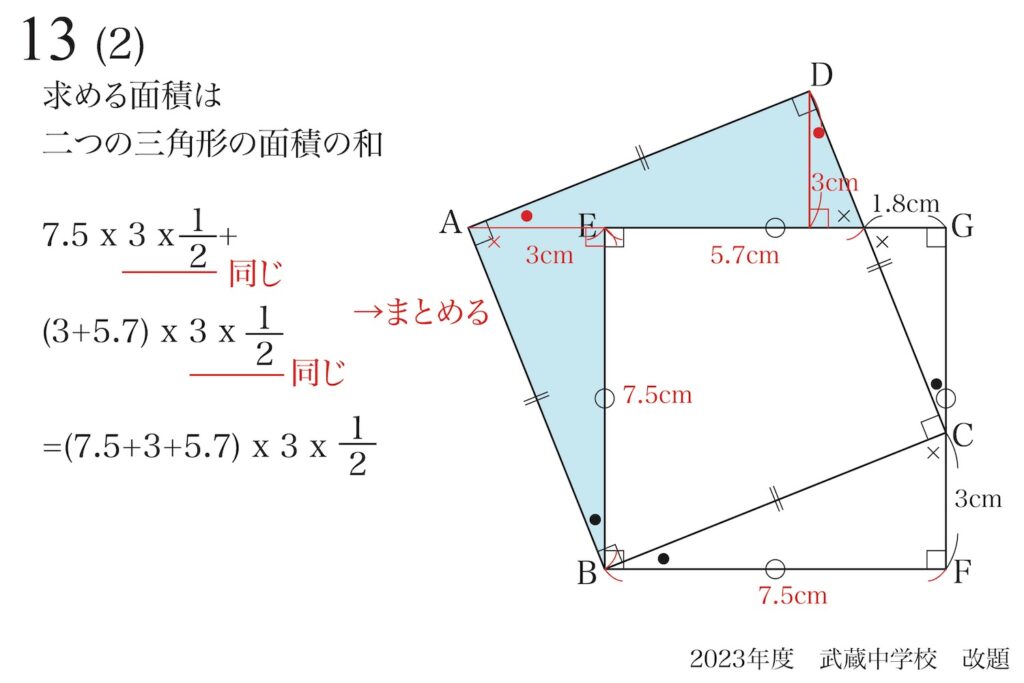
掛け算なので、まとめてしまいましょう。

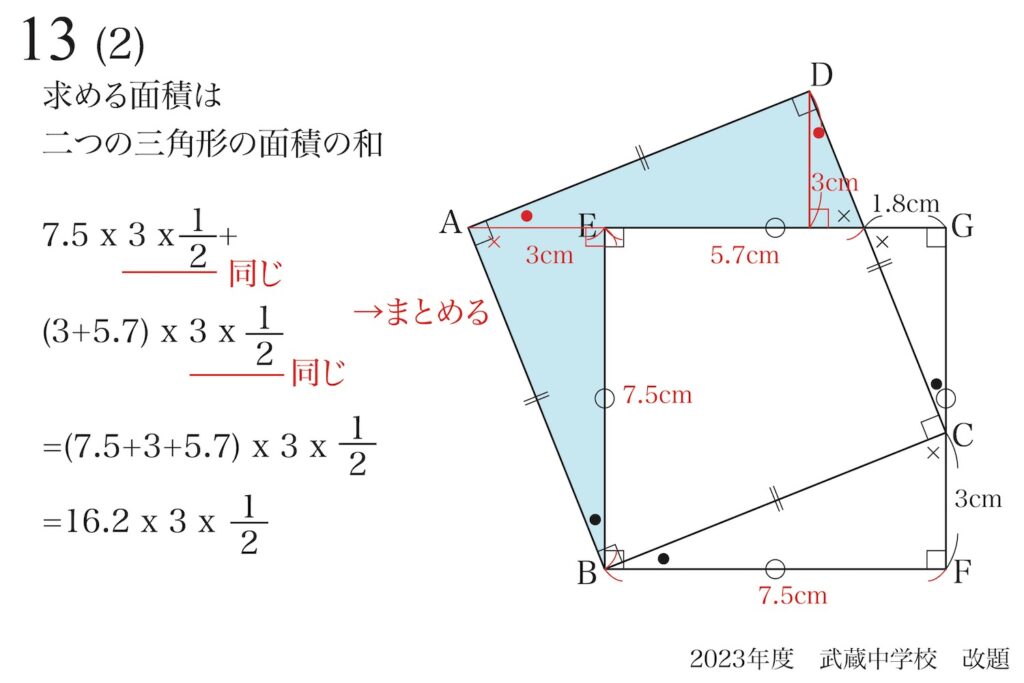
すると、具体的なひっ算をしなくても、ここまでスラスラ進みます。

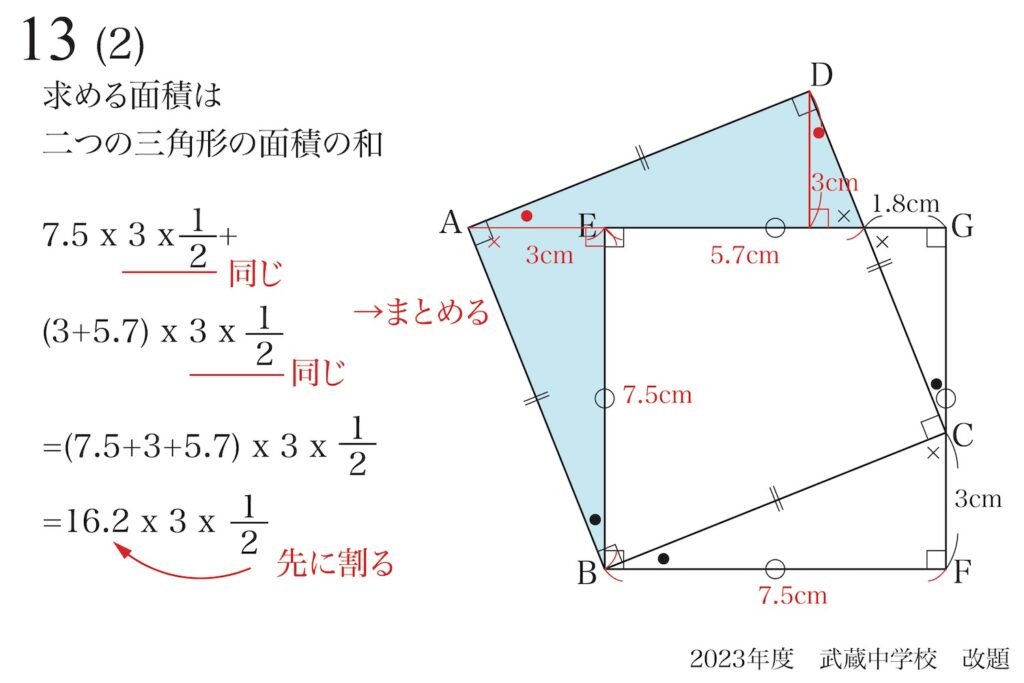
ここで、「掛け算は順番を変えても良い」ことを考えて、先に「16.2×1/2」を計算しましょう。

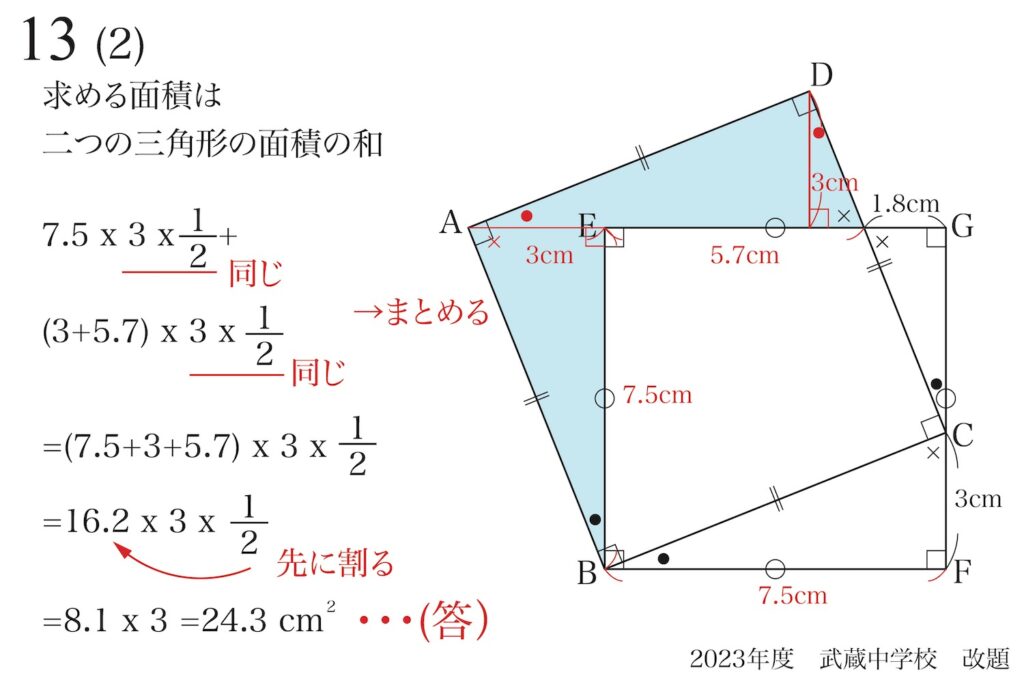
最後は、暗算でも計算できます。

答えが求まりました。

計算ミスを防ぐ方法：暗算を有効活用

この計算方法は「ちょっとしたテクニック」ですが、これが良いかどうかはそれぞれの方の考え方です。

と思うようでしたら、このように効率的に計算してみましょう。

最後の面積計算を「ひたすら計算する」と少し時間がかかります。

また、その結果「計算ミスをする」可能性も増えます。

武蔵中学のように記述式であれば、単純な計算ミスは「ほとんど減点されない」です。

とは言っても、「多少は減点される」でしょう。

計算ミスをする場所にもよりますが、

せっかく考え方や筋道が完全に合っていても、最後の最後で計算ミスしたら1〜2点は減点になります。

その「1〜2点で合否が変わる」可能性があるので、計算は効率的に確実に出来るようにしましょう。

「答えのみ」を記入する問題の場合、残念ながら「分かっていても計算ミスしてはX（バツ）」なのです。

こういう「単純計算ミス」を防ぐためには、下記を心がけましょう。

1の「計算力を上げる・計算する速さを上げる」は誰でも考えることで、まずはこれが大事です。

「計算する速さが、とてもに速い」方もいらっしゃるでしょう。

それは、「かけっこ」で物凄く早く走る方がいることと同様かもしれません。

小学校5,6年生になると「身体能力の違い」が大きく出てきます。

僕が小学生の時に、同じ学年のT君がものすごい速さで走ったのを覚えています。

同学年が120名くらいで、男女半々でしたが、そのT君の走る速さの速さはすごかったです。

シュッと走って行き、僕は全然かないません。

運動会などのリレーでは、T君の番になるとグングン追い越してゆきます。

「早く走れない」方は、こう考えます。

これは仕方のないことで、普通の方は「一定以上の速さで走る」のは無理です。

計算する速さも同様に、特殊な方以外は上限があります。

そこで、「効率的に計算する」ことで短い時間で・かつ正確に計算してみましょう。