前回は「斜めの正方形と補助線のコツ・ポイント〜相似形を見つけるポイント・「似た図形」を探す・難しい形は分割・「良い補助線」を描くコツ・他の補助線と比較・問題 13解法(2)〜」の話でした。
問題 13
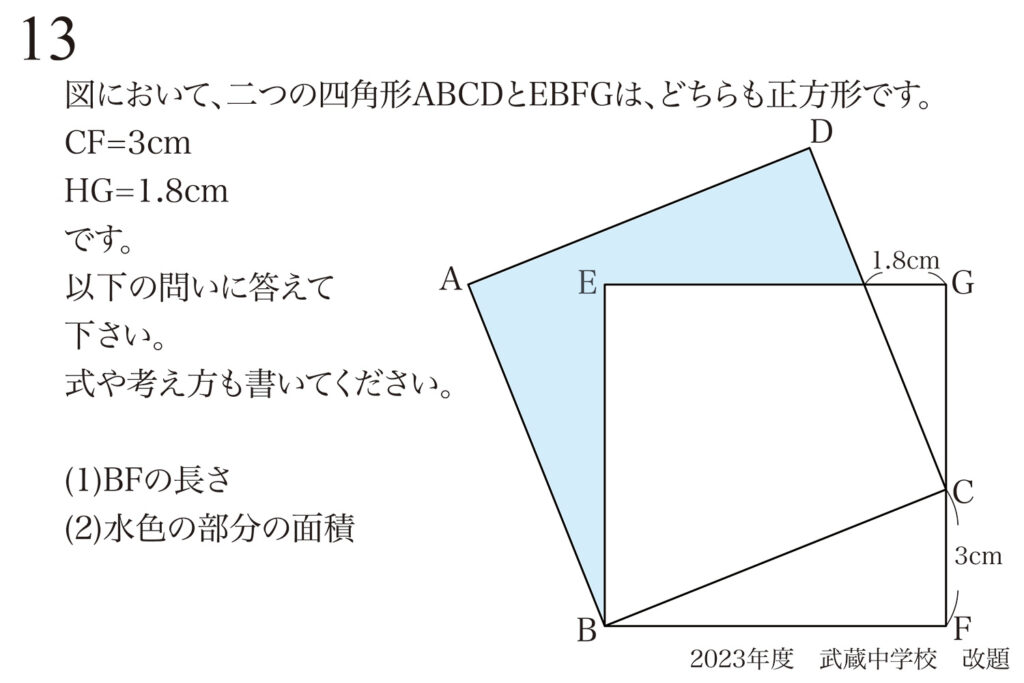
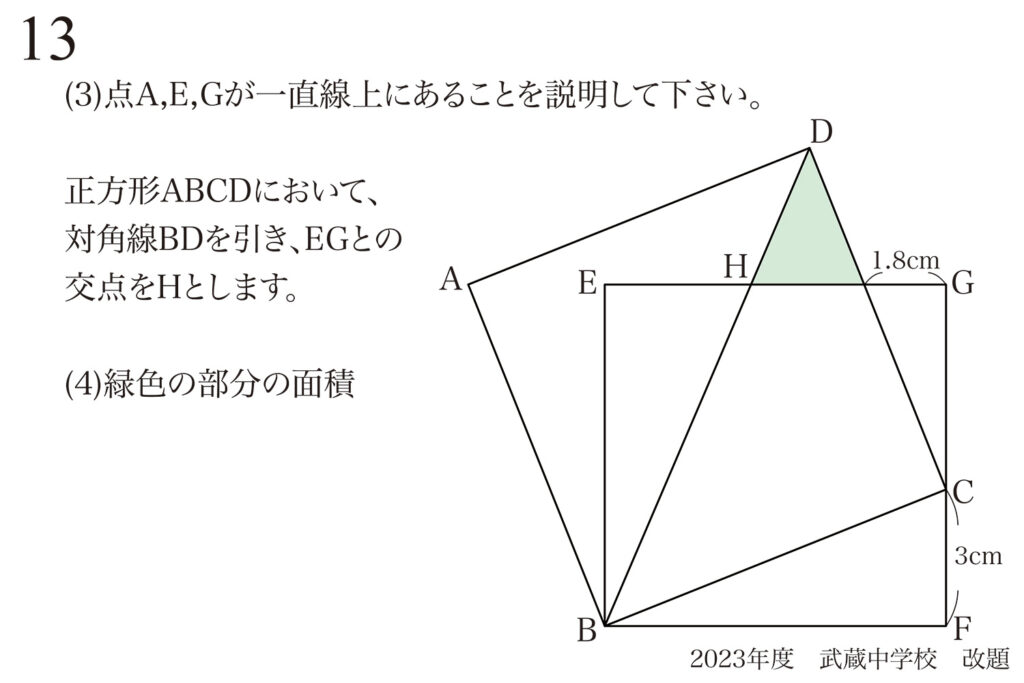
図形の基本性質に着目：2つの正方形は同じ性質
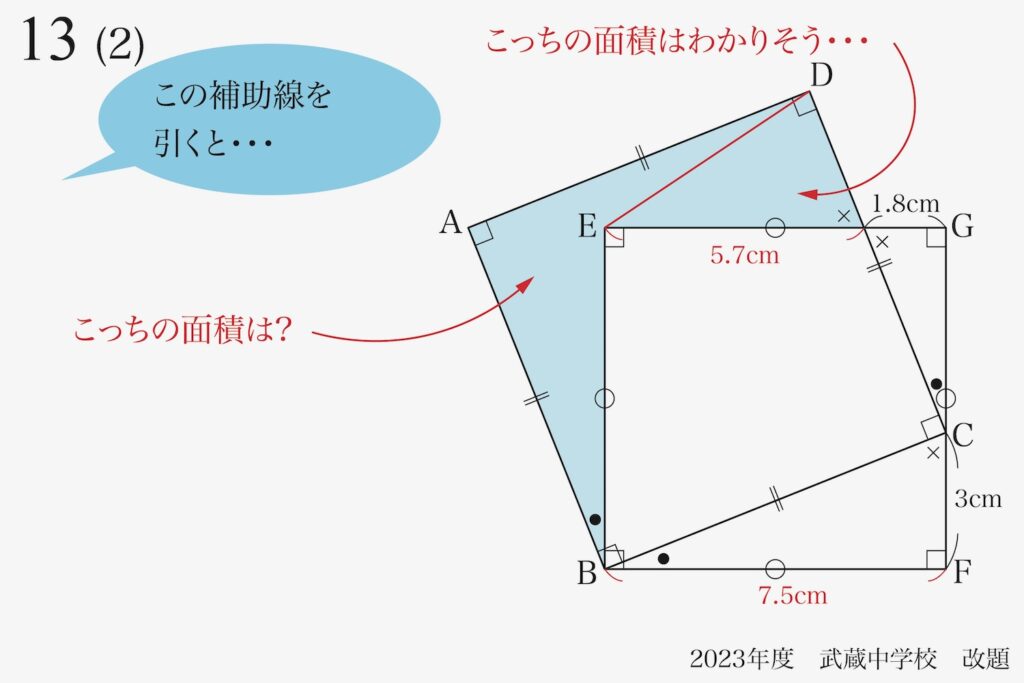
(2)のブルーの面積を考える時、上の補助線を引いて考えました。
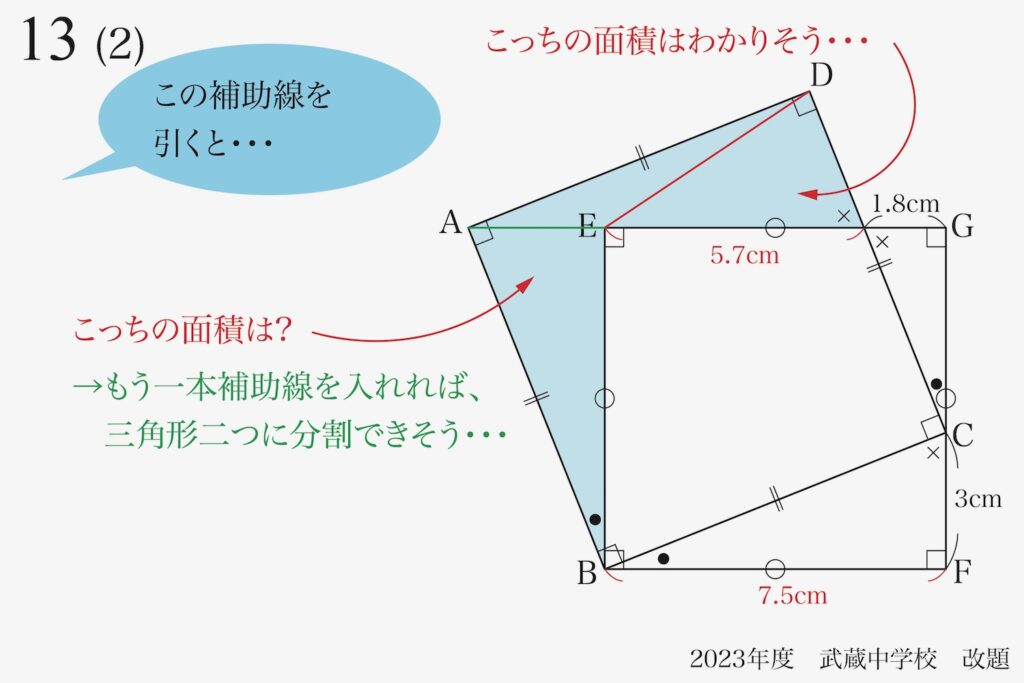
面積は「2本目の補助線」を入れれば、出来そうです。
2本も補助線を引くのは
難しそう・・・
・難しい図形・考える対象は、分ける・分割する
・「分ける・分割する」とき、「分けすぎる」と大変なので、出来るだけシンプルに
難しそうな図形を
分けて、簡単にしたけど・・・
ひょっとして
「分けすぎ」なのかな？
実は「分けすぎ」なので、今回はその理由を考えてみましょう。
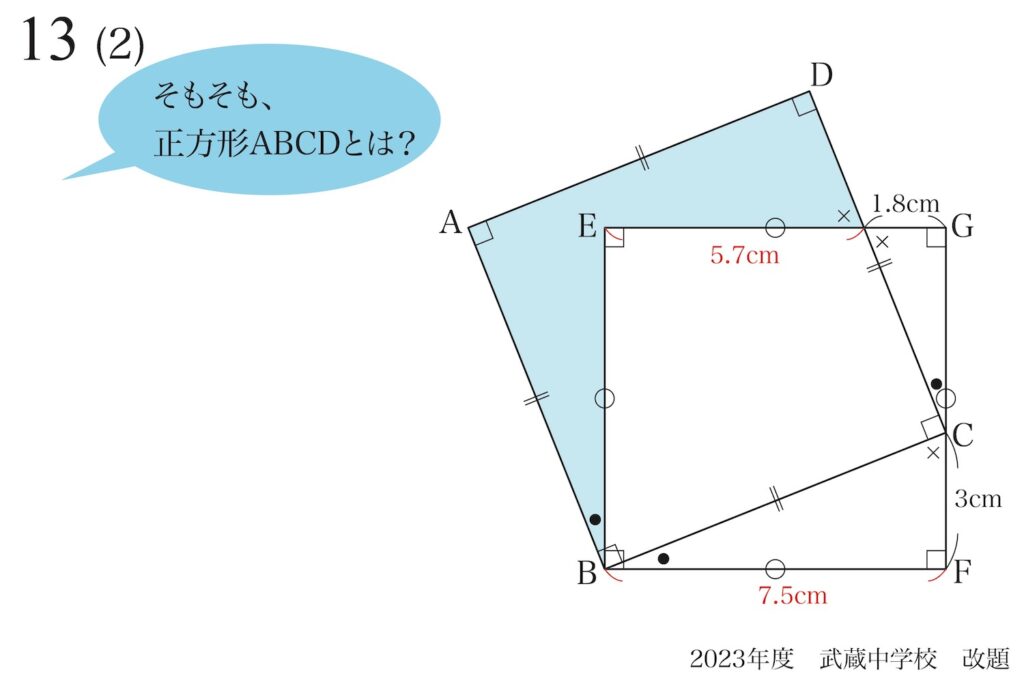
複雑な形状の五角形の面積を求めるにあたり、
補助線を
引いて、図形を分けて・・・
と考えることが基本になります。
三角形や四角形（正方形・長方形・台形・平行四辺形など）の面積は、比較的容易に求められます。
対して、今回の図形のように五角形、あるいは「不整形な図形」は困ります。
これらの「不整形な図形」は、基本的に一度に面積を求めることが出来ません。
「図形を分ける」ことを思いついた後、図形問題では、
次は、
どこの辺の長さが分かるだろう・・・
と考えることが多いでしょう。
このような考え方をすると、「問題のパターン化」につながります。
「次は・・・」という考え方で、パターン・類型化しても良いかもしれません。
図形問題が得意になるためには、基本性質に着目するようにしましょう。
今回の問題では「2つの正方形」という「非常に特殊な図形」が2つも出てきている状況です。
・全ての辺が同じ長さ
・全ての角が同じで直角
確かに二つの正方形は
「同じ性質」だよね・・・
二つあって、片方が斜めだから
難しそうだけど、元は一緒だよね！
「正方形とは何か」を考える・描く
小学校低学年頃に教わる「正方形」は、非常に基本的で簡単な図形です。
方眼紙は全て正方形です。
もし、方眼紙のマスが「長方形や三角形だった時」は、どうなるか考えてみましょう。
それはさ・・・
工作するのが大変になるよ・・・
方眼紙のマスは
「正方形だから、とても役立つ」のね！
「基本的で簡単」な図形ですが、正方形の奥は深く非常に大事な図形です。
正方形とは、どういう図形でしょうか。
四角形で、辺の長さが
全部同じで、角が全て直角。
では、「正方形を描く」を考えてみましょう。
簡単だよ。
真四角を描けばいいよ。
正方形には慣れている方が多いので、パッと描ける方が多いでしょう。
正方形は四つの辺があり、「四つ等辺と直角」を一気にイメージして描くことができると思います。
辺も角も対象が4つありますが、「全部同じ」だからイメージしやすいでしょう。
確かに
そうね！
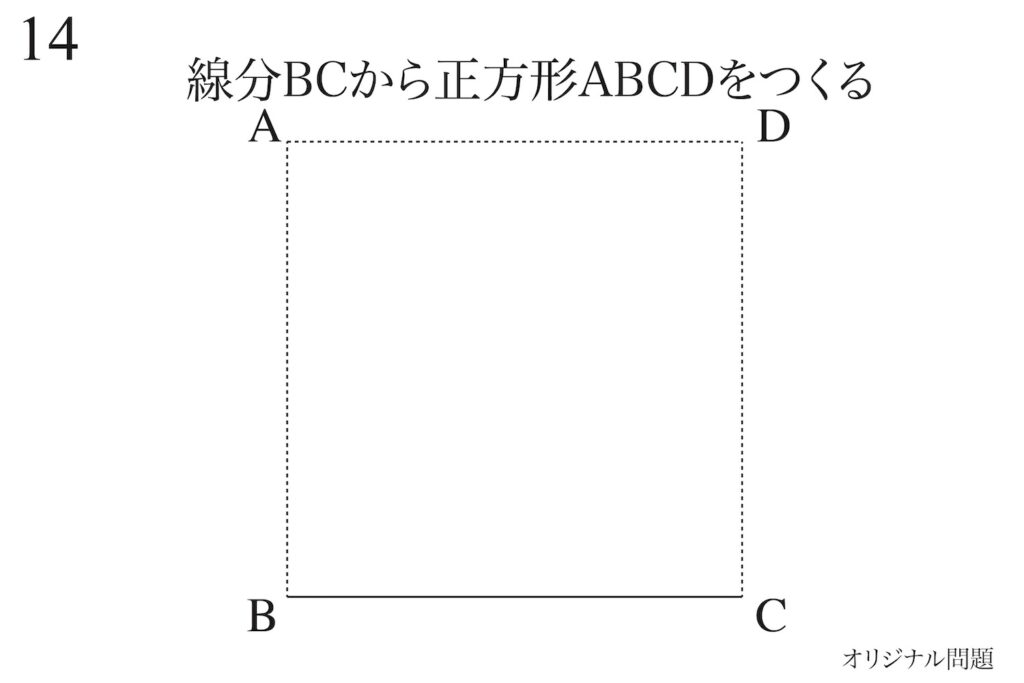
上の辺BCから正方形ABCDを作ってみましょう。
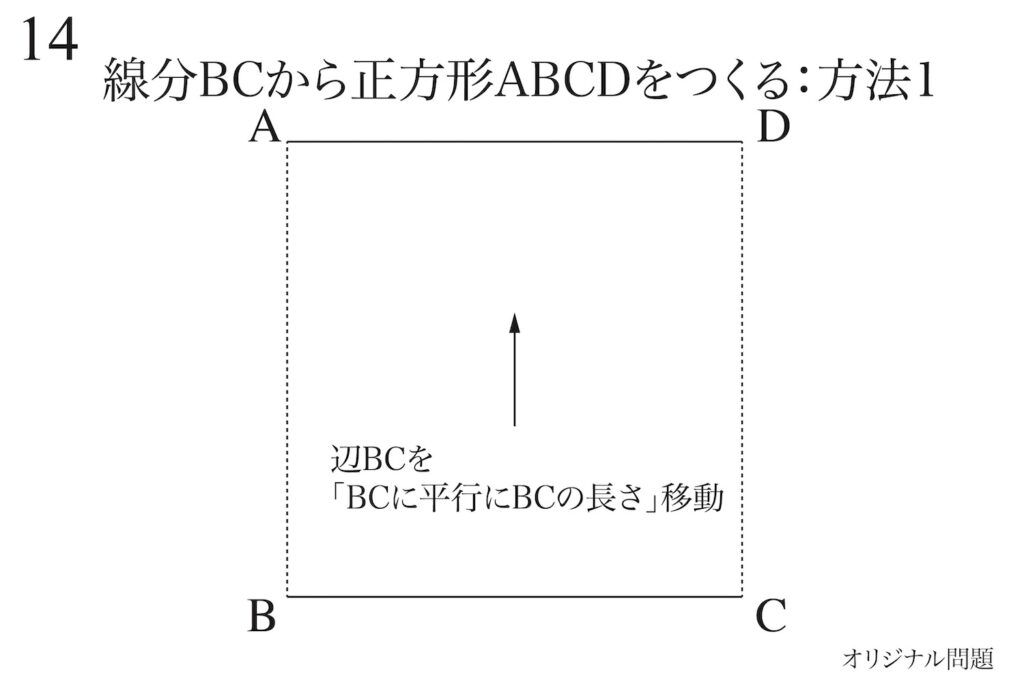
一辺を「その辺と同じ長さ」平行移動すれば、正方形を作ることができます。
別の方法で正方形ABCDを作ってみましょう。
別の方法？
一つ出来たら、良いんじゃない？
あることに対して「複数の方法」を理解しておくと、応用力が広まります。
もう一つの方法は、
直角を使うのかな？
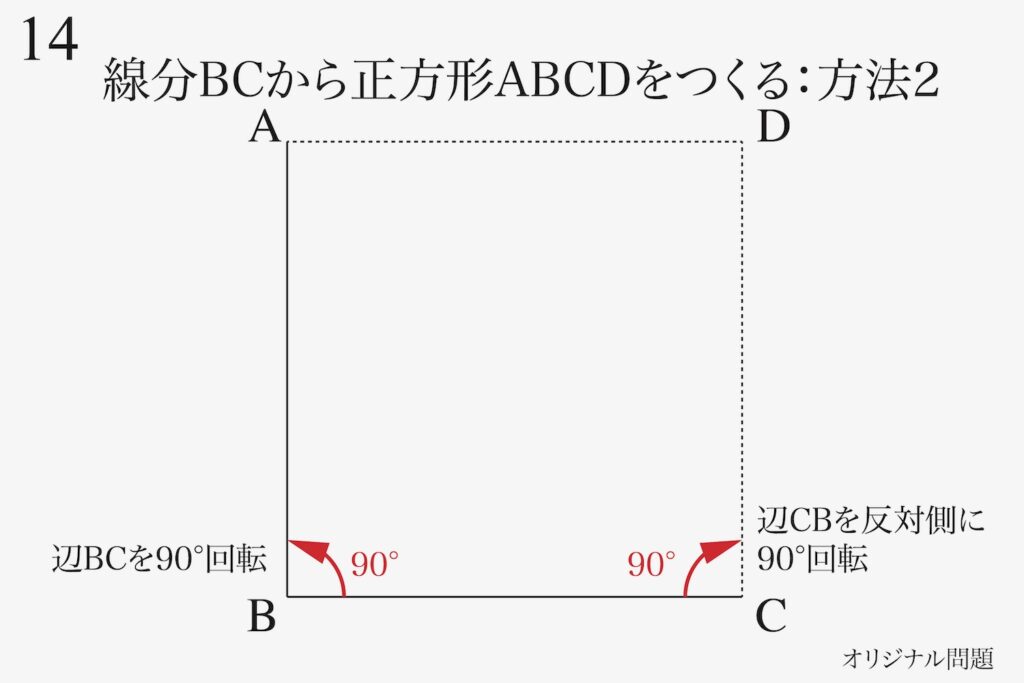
辺BCを90度、反対側に90度回転すると正方形が見えてきます。
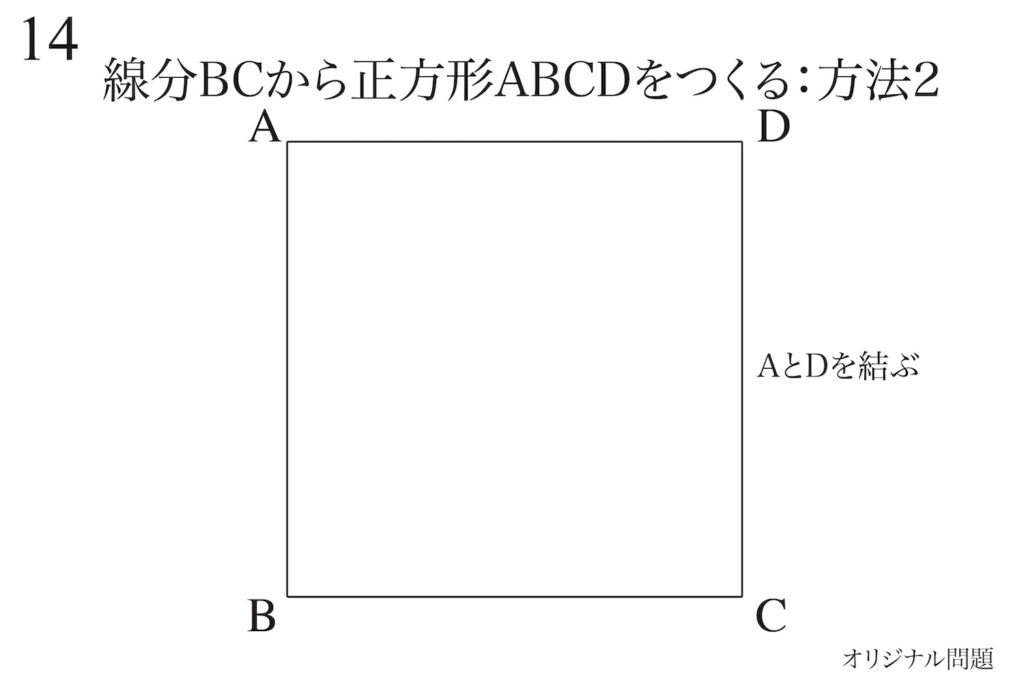
こうして、しっかり
正方形を描くと面白いね！
これで正方形の作り方・描き方が二つ分かりました。
このように、あることの考え方を複数理解すること、別解を考えることは大きな応用力向上になります。
・あることやある図形を複数の視点から考える
・問題の別解を理解する
対象が2つまでは比較的簡単ですが、対象が3つ以上になると、非常に難しくなります。
多くの中学受験生、中学生以上の方が「苦手」と感じることが多い電気の問題。
なぜ「難しい」と感じる方が多いのかは「電流・電圧・抵抗の3つが登場する」からです。
もし、電気で登場するのが「電圧と電流だけ」だったら、どうでしょうか。
それなら
簡単だよ！
どれか2つだったら比較的簡単ですが、3つになると難しくなってしまいます。
そこで、電気の問題では「電圧を主役に考える」話をご紹介しました。
正方形は「辺も角も対象が4つもある図形」です。
「4つもある図形」ですが、「対象の辺も角も4つ全部同じ図形」なので簡単です。
「全部同じ」であれば、対象が多くなってもイメージしやすいです。
そして、「とても簡単だけど、奥が深い」のが正方形です。
「固定された点や線」に着目
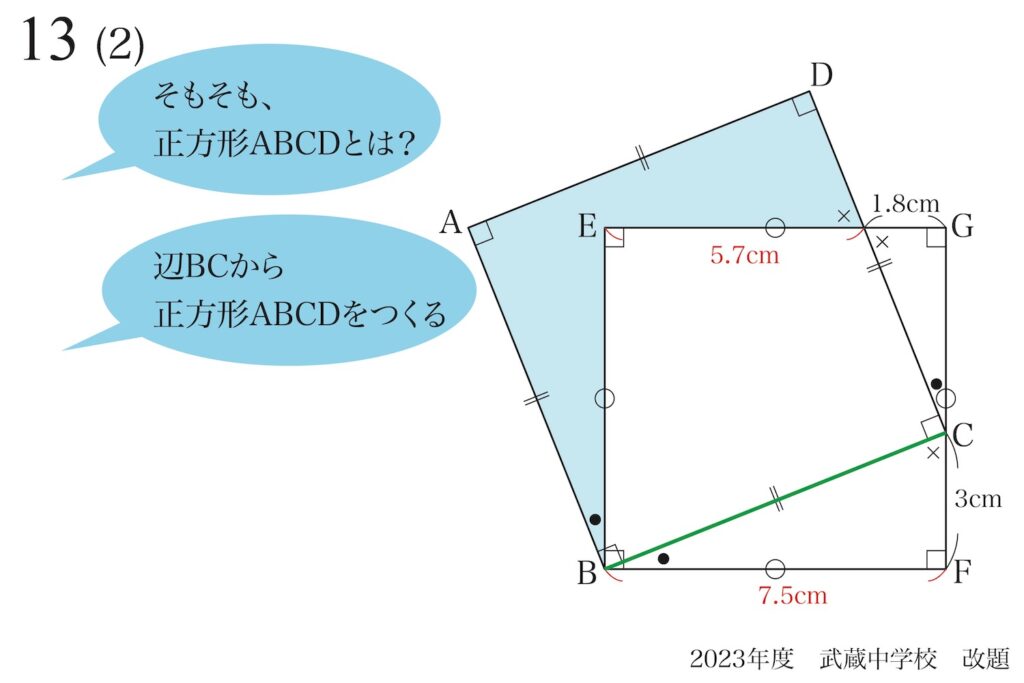
正方形の基本性質・骨格を考えてみましょう。
「4つの辺を一気に描ける」ですが、「辺BCを一辺（底辺）とする正方形を描く」ことを考えましょう。
どのように描くか考えてみましょう。
他の3つの
辺の長さはBCと同じで・・・
全部直角だから、
さっきと同じように考えれば描ける！
「一気に他の3つの辺を描く」のは難しいですから、「一辺ずつ描いて」みましょう。
辺BCを同じ長さだけ
平行移動してもいいね！
それでも描けるけど、
「平行移動」はちょっと唐突な感じ・・・
平行移動することは図形的発想ですが、「グッと辺が向こうに行ってしまう」感じがあります。
まずは「辺BCと同じ長さで、辺BCに直行する（直角の）辺BAを描く」やり方にしましょう。
これだと、辺が一気に向こうに
行ってしまわないね・・・
新しい辺が、
近くにあるから考えやすそう・・・
ここで大事なポイントは、「どちらででも良い」ですが「考えやすいのはどちらか」です。
「辺を90度回転」だと、「回転する点は固定」なので考えやすそうです。
・複数の考え方があるときは、対象に対して「考えやすい」考え方を選ぶ
・図形問題では「固定された点や線」があると「考えやすい」ことが多い
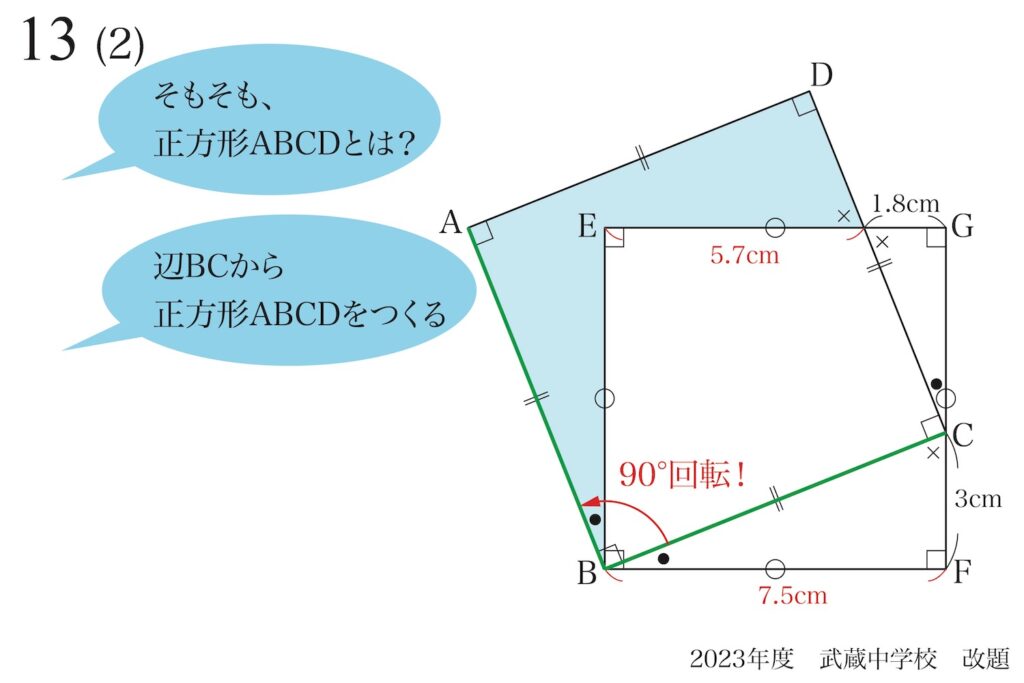
この時、「辺BCを90°回転すれば辺BAになる」と考えることもできます。
確かに
そう考えることができるね！
残りの2つの辺は「それぞれの辺を90°回転する」や「辺BCと辺BAを折り返す」で作れます。
少し考えてみる大事さ：「急がば回れ」で学力向上
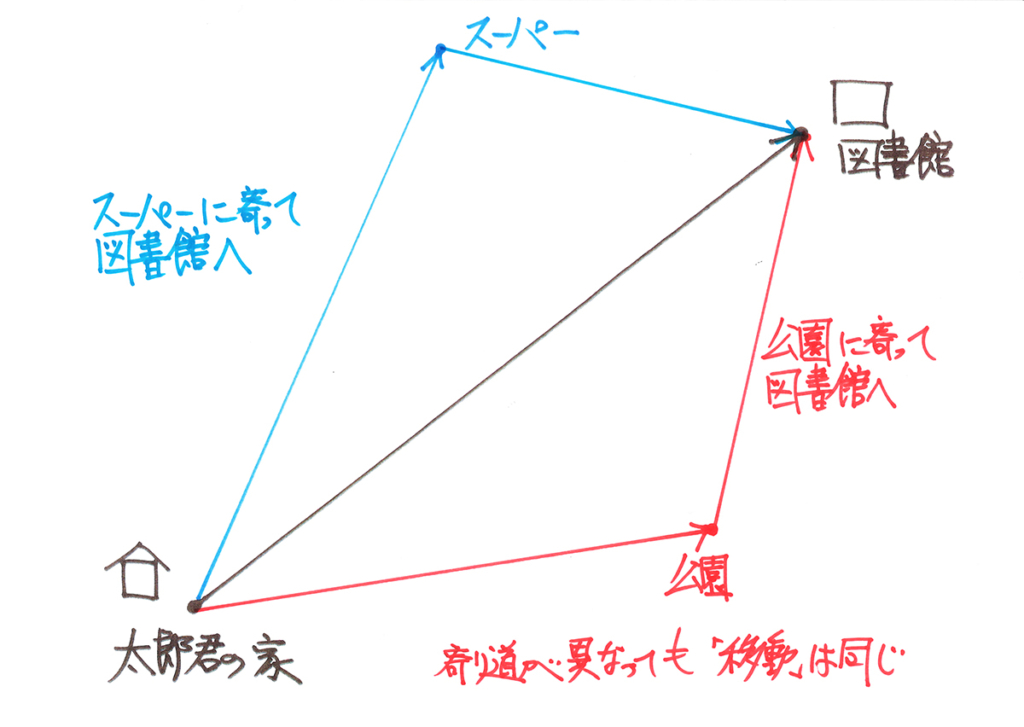
ここで、「矢印の話」で考えてみましょう。
算数実践問題10では、「矢印の辺1つ」を「矢印の辺2つに分けて」考えてみました。
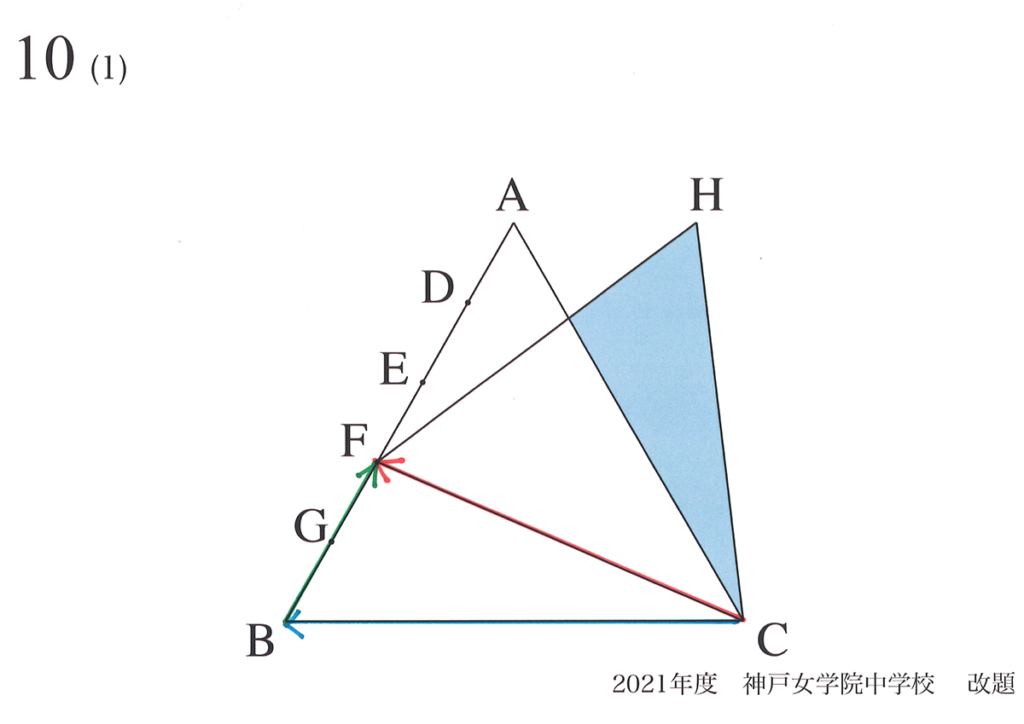
上の図形で「辺CFの矢印=辺CBの矢印+辺BFの矢印」と分けて、60°回転させます。
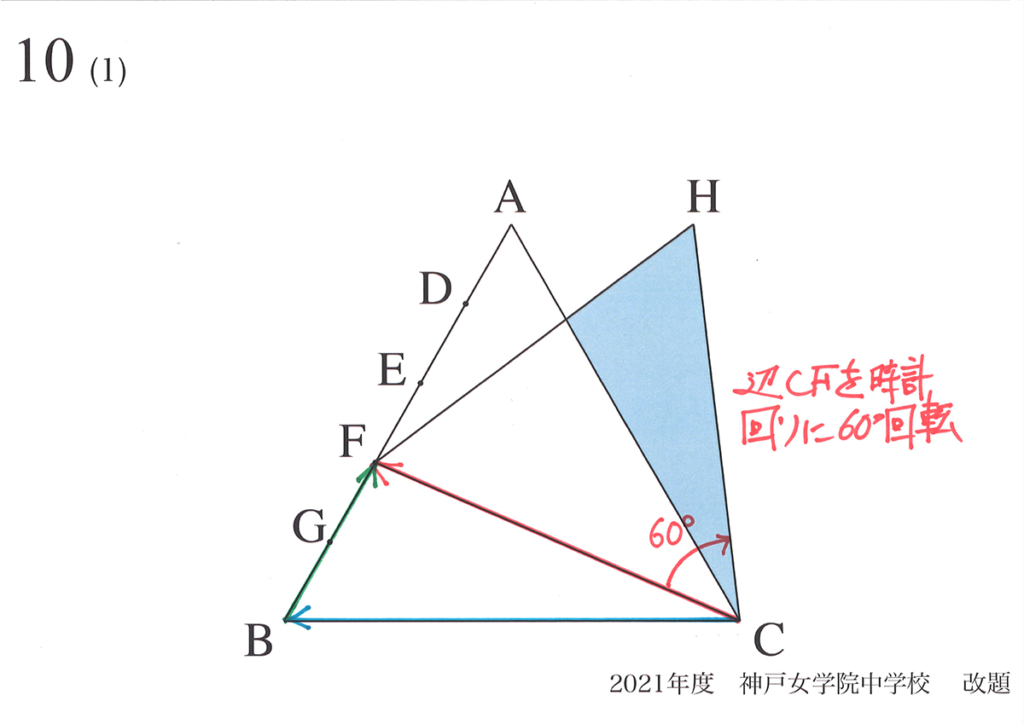
このようにして「正三角形FCHをつくる」ことを考えて、様々なことがわかりました。
今回も同じ考え方で、考えてみましょう。
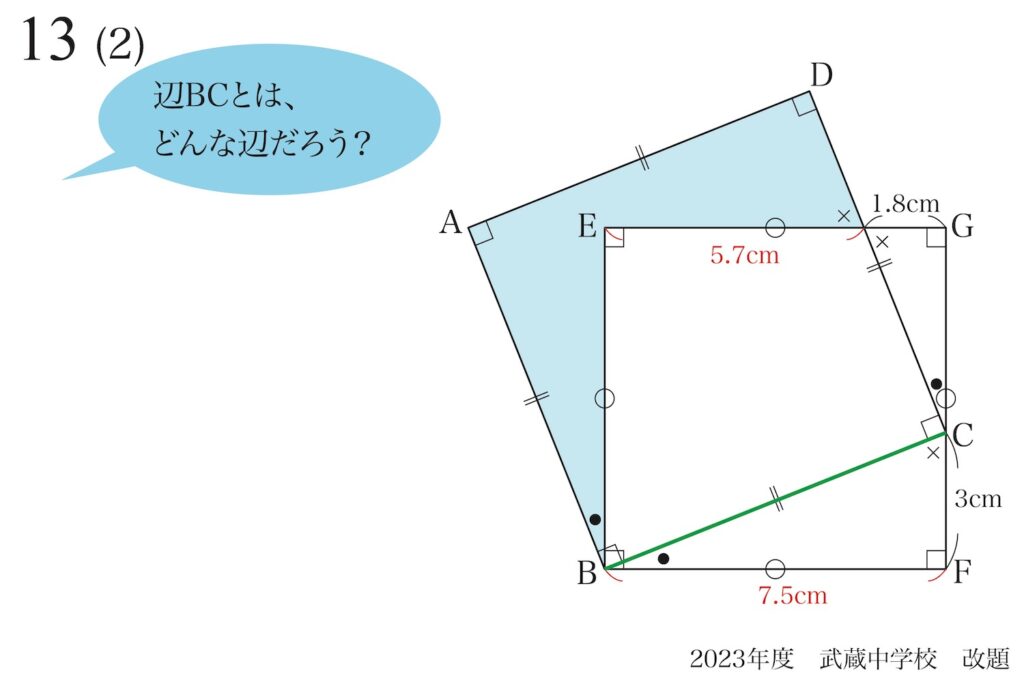
問題10では「正三角形を考える」でしたが、本問では「正方形を考える」です。
辺BCを矢印BCと考えて「正方形ABCDをつくる」を考えてみましょう。
考え方は次回ご紹介します。
次回の話を見たら、
なんだ。
そういうことか・・・
思ったより
簡単！
と感じる方が多いでしょう。
算数・数学は「考えて出来る」が良いのですが、「出来るなら勉強しなくても良い」ことになります。
「出来ないことがある」から勉強するので、「出来る、出来ない」は別として少し考えるをやってみましょう。
そこで、何か
あれ、
ひょっとして・・・
と気づくことが少しでもあれば、とっても良いです。
そうして「自分で気づいたこと」は忘れないです。
教わることは、聞いたとき、
よし！
わかったぞ！
となりますが、少し時間が経つと、
あれ・・・
どう考えるんだっけ・・・
となることが多いです。
問題をたくさん解いて、数多くの考え方を学ぶのも良いです。
「少し考えて、しっかり身につける」姿勢も大事です。
科目も多く、たくさんやることがある受験生は「時間が気になる」方が多いでしょう。
「急がば回れ」という諺もありますが、「少し考えて（遠回りして）学力を上げる」も大切な姿勢です。
・急がば回れ=遠回りして、色々と考えてみる
・「自分で気づいたこと」は忘れないので、大事に
