前回は「斜めの正方形と相似形と長さのポイント〜「一組の相似形」発見・問題の条件を振り返る姿勢・直角三角形の辺の長さ・描いた条件から発見・条件を組み合わせて立式・問題 13解法(1)〜」の話でした。
問題 13
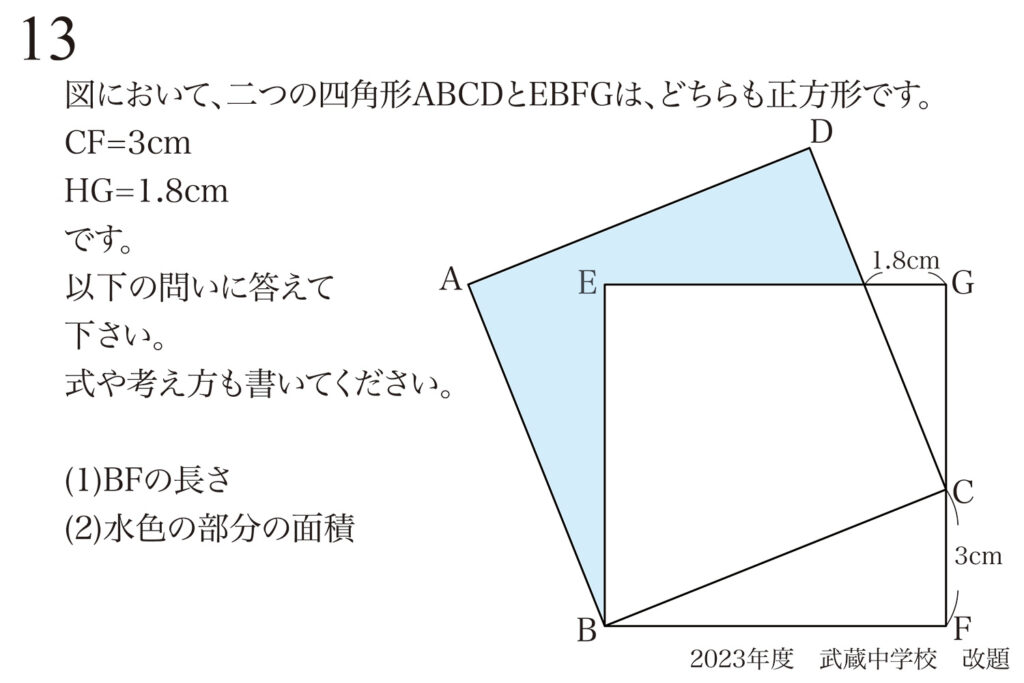
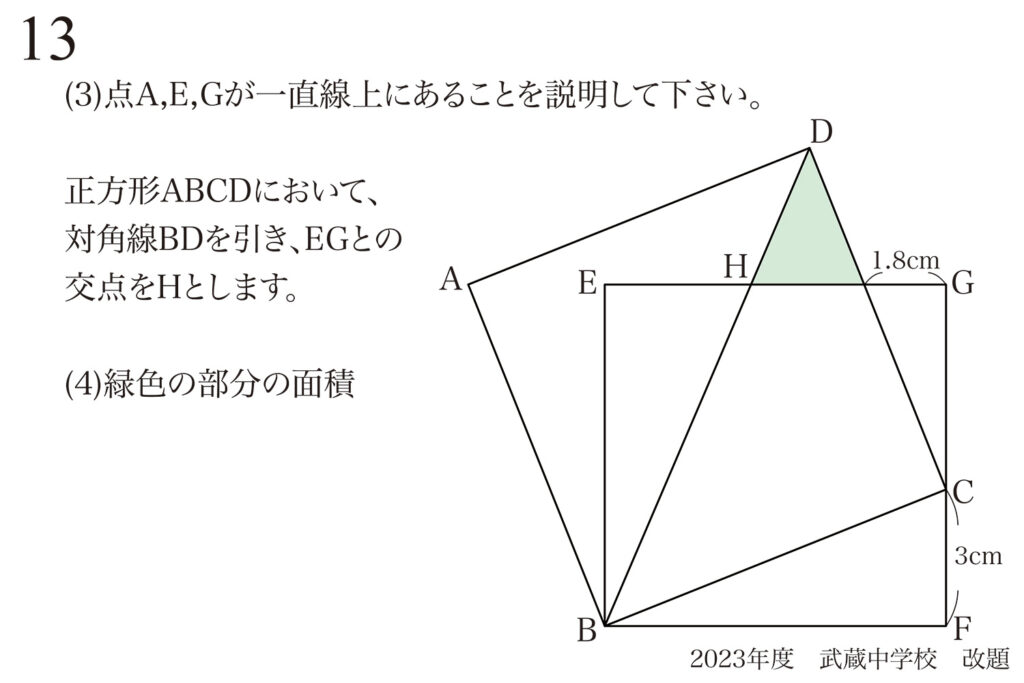
相似形を見つけるポイント：「似た図形」を探す
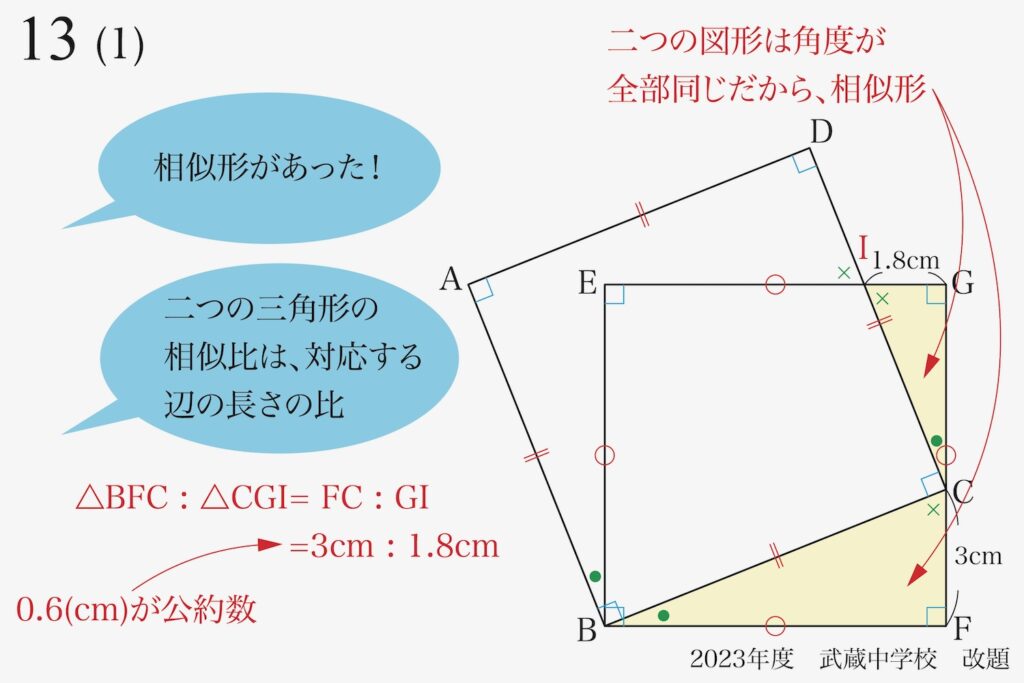
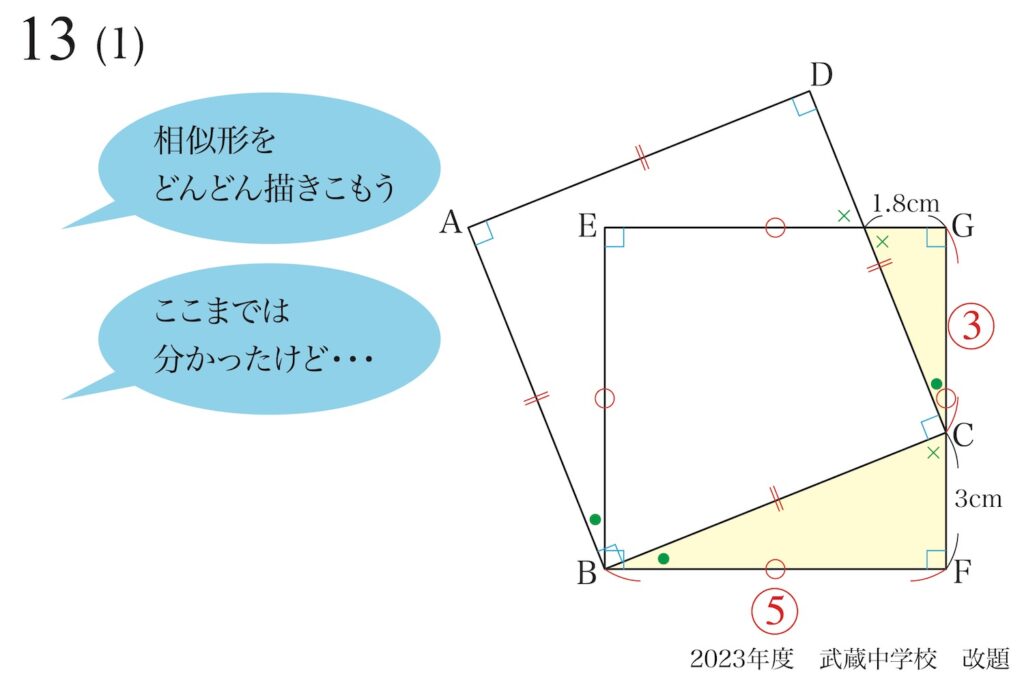
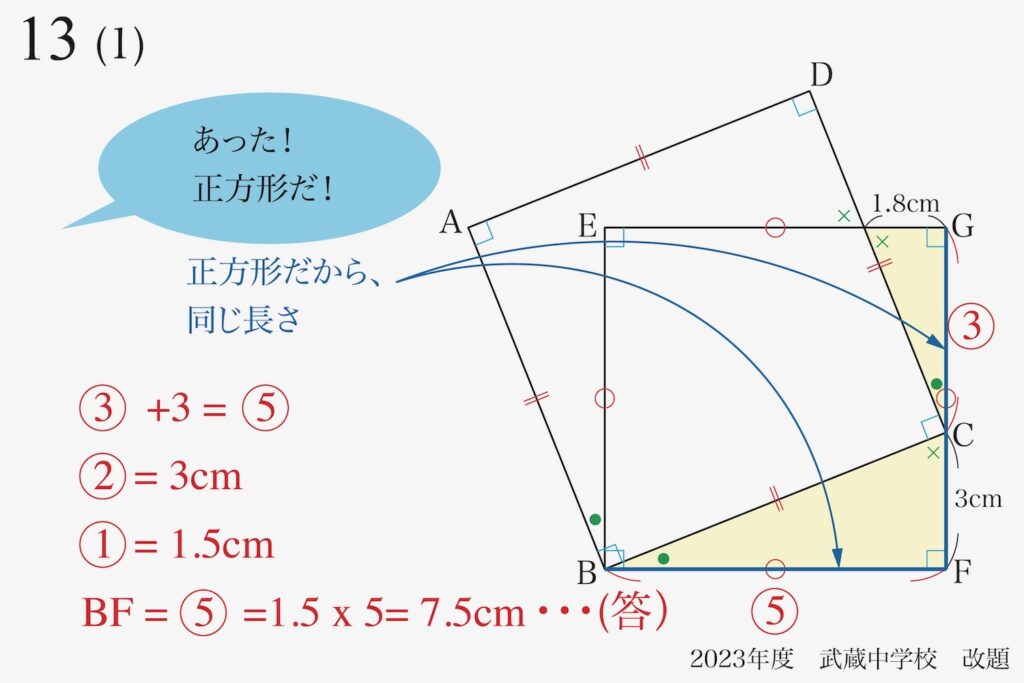
(1)の「BFの長さ」を求める際には、まずは相似形を発見しました。
・ある形AとBが「相似」
→片方の図形を拡大・縮小すれば、もう一方の図形となる
・相似の条件
←→対応する角度が同一
←→対応する辺の比が同一
「補助線を引いて、相似形を見つける・発見する」問題もありますが、「図形の中に相似形がある」ことも多いです。
男子小学生図形の中に相似形があるのか、
ないのかはパッとわかる方法があるの？
図形問題によるので「パッと分かる鉄則」はないように思います。
男子小学生そっか・・・
ないんだ・・・
一つの考え方としては、「図形の中に似た図形を探す」のも良いでしょう。
相似形は「ある図形とある図形が相似」で、「相（互いに）似ている」図形です。
女子小学生確かに「相似」っていう
言葉はそうね！
「問題の図形をジッと見て、似ている図形を探す」と相似形が見つかる可能性が高まるでしょう。
・「相似」は「相（互いに）似ている」図形だから、似ている図形を探す
・相似形は、同じ向きではなく「互いに直角」など向きが異なることがある
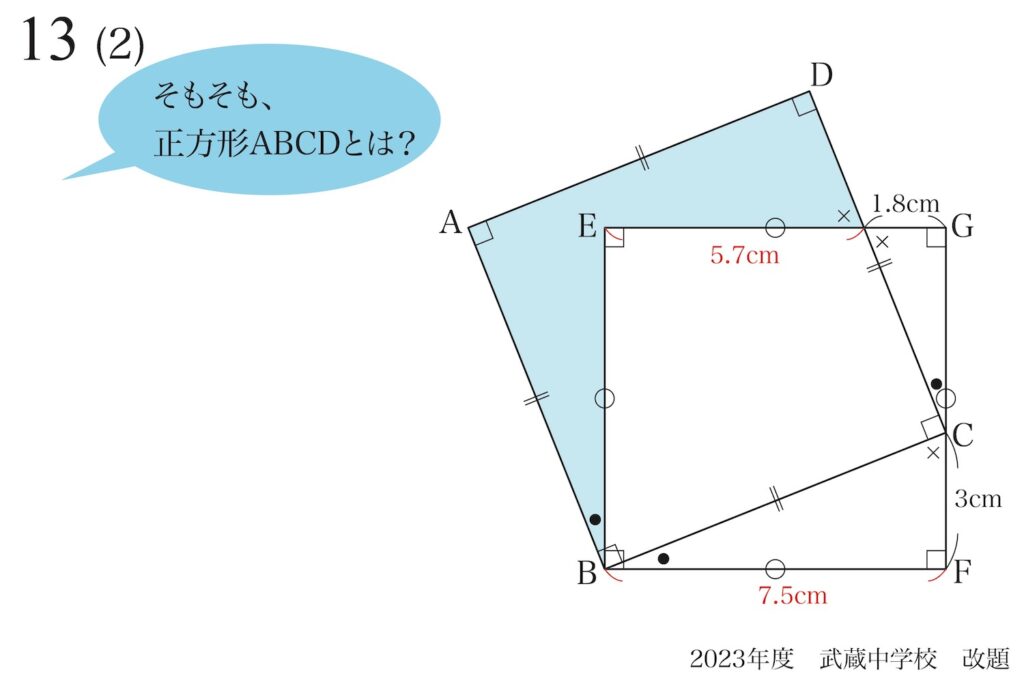
この問題では、黄色の相似形同士が「互いに直角」である点が、少し相似形と気づきにくい点です。
・「何か使っていない条件」を探す
・分かったことと「問題の条件」を組み合わせる
図形問題に限らず、問題を解いている途中手が止まったら、「他の条件を探す」ようにしましょう。
・全ての辺が同じ長さ
・全ての角が同じで直角
正方形は非常に特殊で「基本となる図形」です。
「三角形の中にいくつか正方形がある」問題などもあります。
これらの問題を考えるときは、正方形の問題は「正方形の性質」を強く意識しましょう。
「基本的考え方」をしっかり身につけて学力アップ
この(2)の問題は、図形問題の非常に大事なことがたくさん詰まっている良問です。
男子小学生似た問題を
やったことあるよ！
類題を解いたことがある方もいらっしゃるでしょう。
女子小学生そう言えば、今回は
小問が4つあるから、前後の問題が関係あるのかな？
1.最後の問題のみだと難しいため、ヒントを作って解きやすくする
2.問題を分け、出来る部分を明確にして、採点の際に点数の差が出やすくする
試験の後半の図形問題や文章題では、小問に分かれていることが多いです。
その場合は、「前の問題が後ろの問題のヒント」の場合があるので、意識しましょう。
女子小学生(1)の考え方が
使えるのかな？
問題を考えながら「(1)で分かったこと・考えたこと」を意識します。
算数・数学の基本的なことを学んだ上で、少し難しめの問題を解いた時、
女子小学生解答を読めば
分かるけど・・・
女子小学生どう勉強したら、
こういう解法が思いつくの？
このように「どう勉強したら良いか」と思う方が多いと思います。
この時、
塾講師算数・数学は、
数多くの解法のパターンを頭に入れることが大事！
このような「解法パターンの強化」という勉強の仕方もあります。
実際に「数多くの解法パターンを頭に入れる」ことは、「近道の一つ」かもしれません。
「決められた時間内での解決力アップ」に対して、効率的側面があります。
すると、
男子小学生では、やっぱり、
たくさんのパターンを習得するのが良いんだ・・・
女子小学生たくさん
解法パターンを覚えよう！
こう考える方も多いでしょう。
今年あるいは過去において、中学受験〜大学受験で合格した先輩たちの中にも、
男子中学生たくさんパターンを
覚えた方が早いぜ！
こう話す方もいらっしゃるでしょう。
中学受験の小学生・高校受験の中学生は、塾や先生の方針によると思います。
大学受験の高校生は、最終的には「自分で学ぶ姿勢」は「それまでの学び方で決定」するのでしょう。
「解法パターンを多く身につける」考え方も良いかもしれません。
ここでは、「基本的考え方」をしっかり身につける考え方をご紹介します。
斜めの正方形と補助線のコツ・ポイント：難しい形は分割
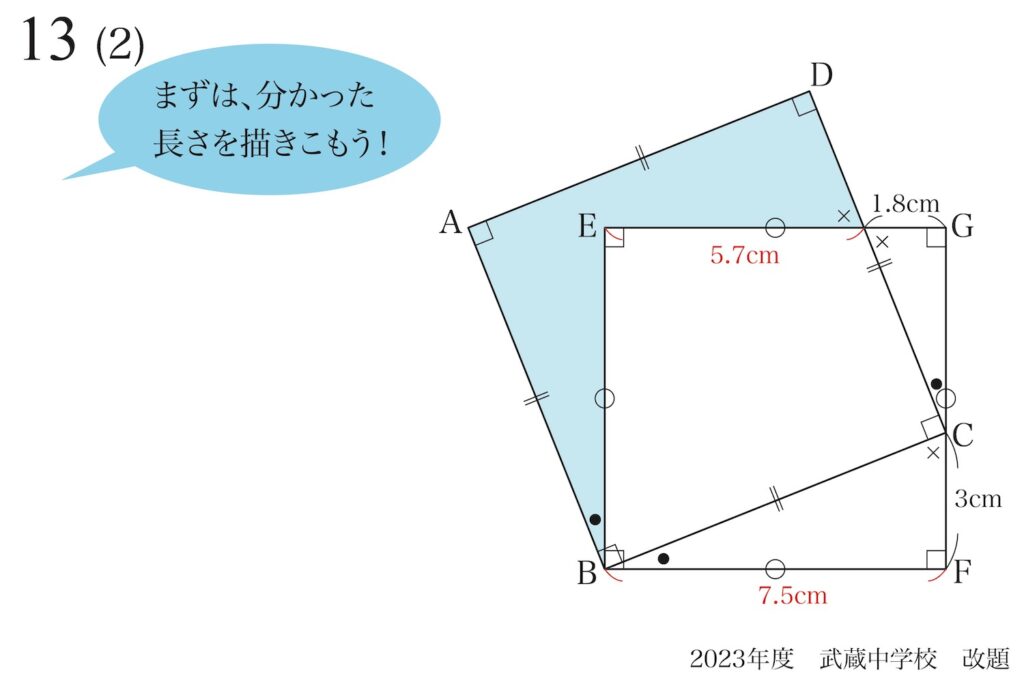
こういう小問に分かれた問題は、「分かったこと」を前提に次に進みます。
図形問題では、「分かった長さ・角度」などを図形に描きましょう。
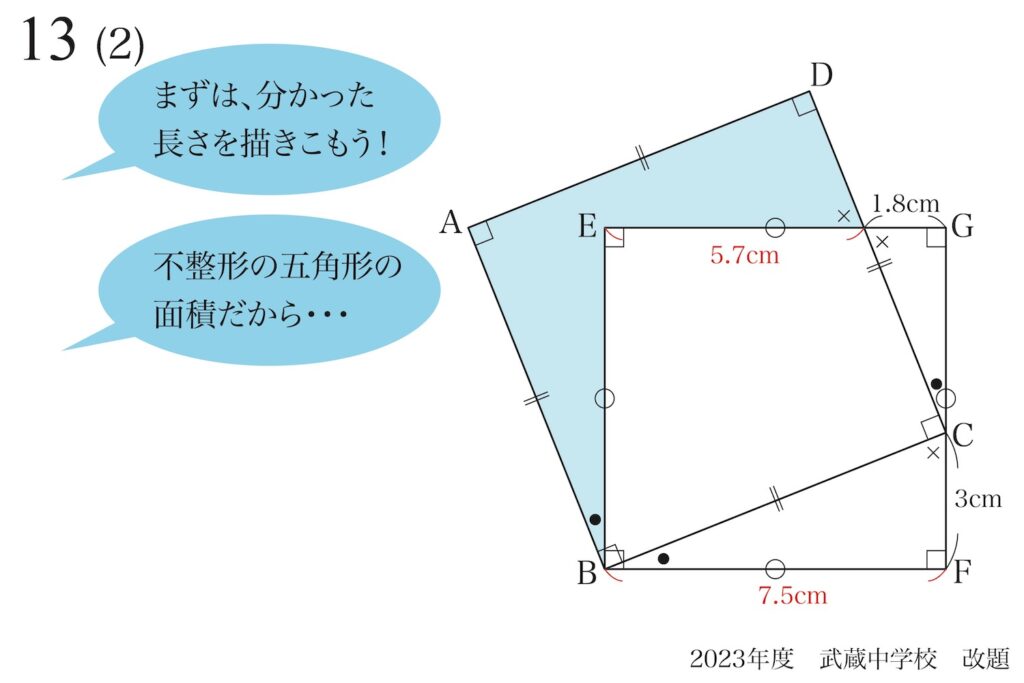
答える面積の図形は「不整形の五角形」の面積です。
この面積を「一気に求める」のは難しいです。
「一気にやるのが難しい」時は、「分割する・分ける」のが算数・数学の大事な基本です。
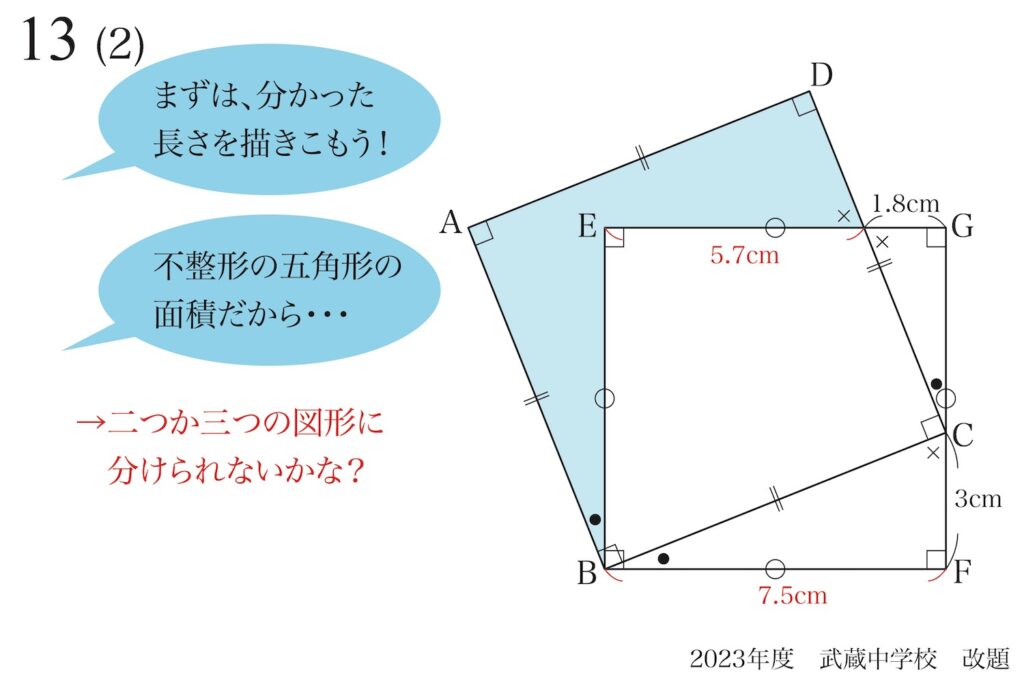
そして、
男子小学生2つか3つくらいの
図形に分けられないか？
図形を分けることを考えてみましょう。
分ける図形の数は少ない方が考えやすいです。
あまり多くの図形に分割すると「考えることが増えてしまう」ので、シンプルにしましょう。
・難しい図形・考える対象は、分ける・分割する
・「分ける・分割する」とき、「分けすぎる」と大変なので、出来るだけシンプルに
「良い補助線」を描くコツ：他の補助線と比較
改めて、問題のブルーの図形を「分ける」ことを考えてみましょう。
男子小学生やっぱり
補助線入れないと出来ないね・・・
こういう問題の解法では、
塾講師こう補助線を
入れると分かる！
このように「補助線を入れる」解法を教わると、
男子小学生なぜ、その補助線が
思いつくの？
このように感じる方が多いでしょう。
筆者も小学校6年生の時、模擬試験の図形問題で、
小学生の筆者この補助線が分かれば
良いけど・・・
このように「補助線が出てこない」ことを悩んだ記憶があります。
「良い補助線を引く」のは、ヒラメキでもセンスでもなく、「描いていると見えてくる」のです。
男子小学生見えるように
なるの？
慣れてくると勘が磨かれてきて、なんとなく、
内野吉貴この補助線が
良さそうかな？
このように、良い補助線がパッと分かるようになります。
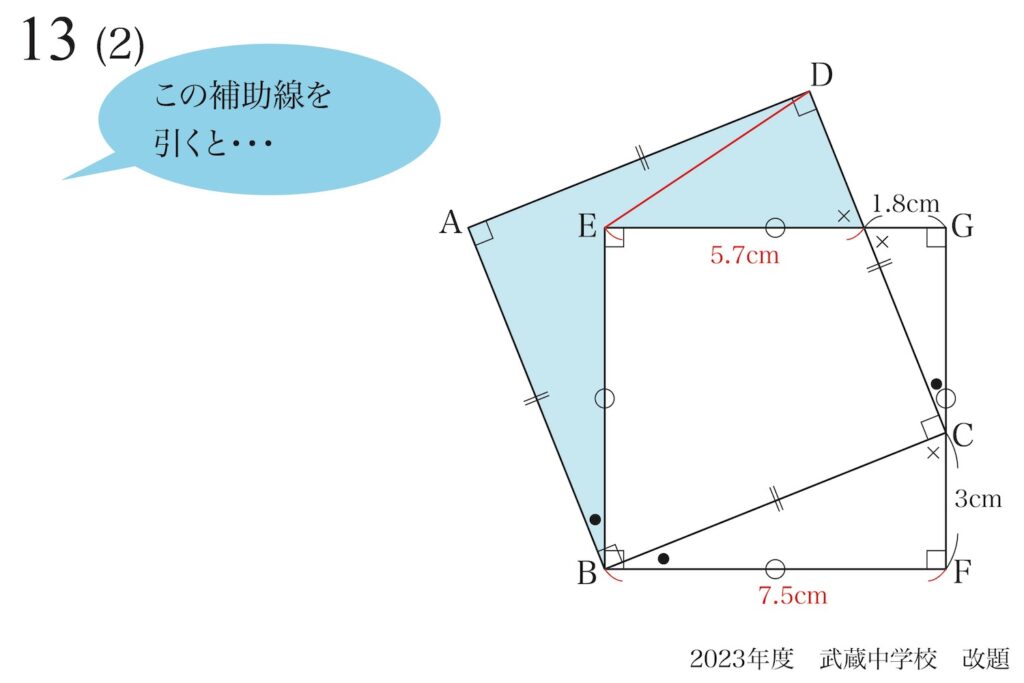
今回は、色々と補助線を考えてみましょう。
例えば、このような補助線を引いてみました。
五角形の図形が、三角形と不整形の四角形に分かれました。
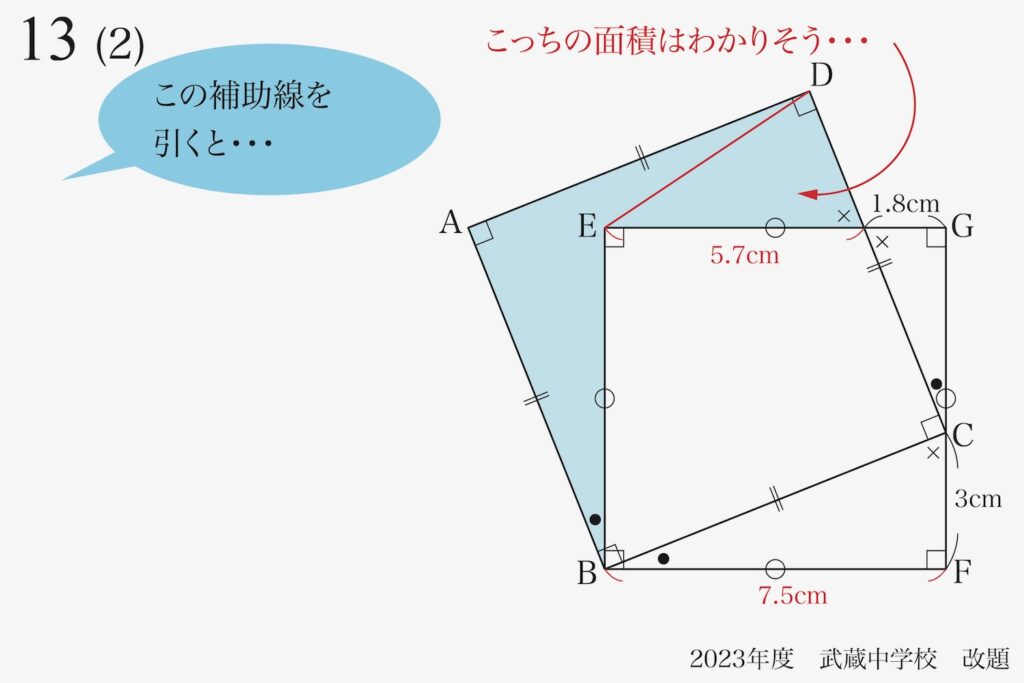
三角形の面積は分かりそうですが、不整形の四角形の面積は求めるのが難しそうです。
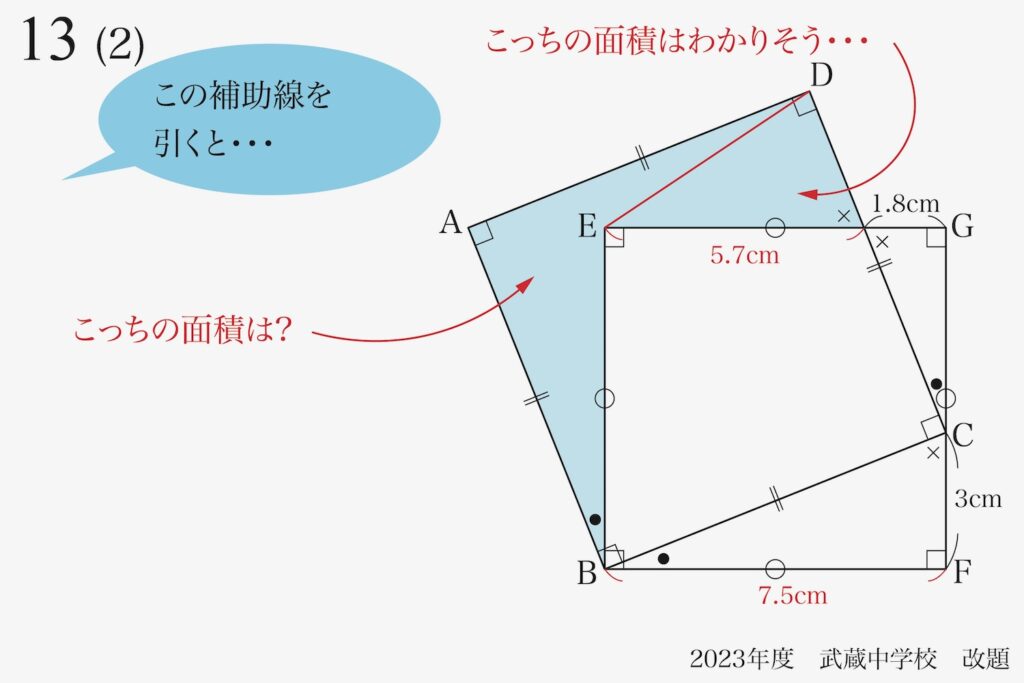
女子小学生これは
ちょっと大変そうね・・・
男子小学生もう一本
補助線入れてみようか？
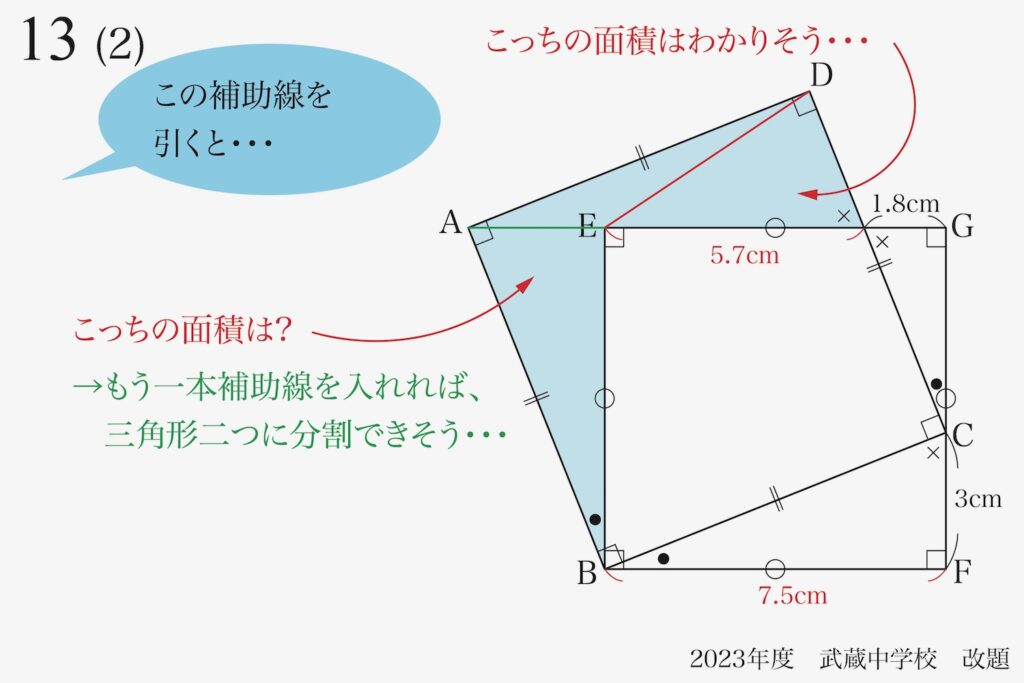
この不整形の四角形の面積は、もう一本補助線を入れれば、「分かりやすい三角形に分割」出来ます。
すると、面積が求まりそうです。
男子小学生よしっ！これで、
辺の長さを求めてゆけば良いんだ！
このように分割して考えても解けます。
ここで、「正方形の条件」を思い出しましょう。
「正方形」というのは、非常に特殊な基本的図形です。
正方形の性質と描き方・作り方をもう一度考えてみましょう。
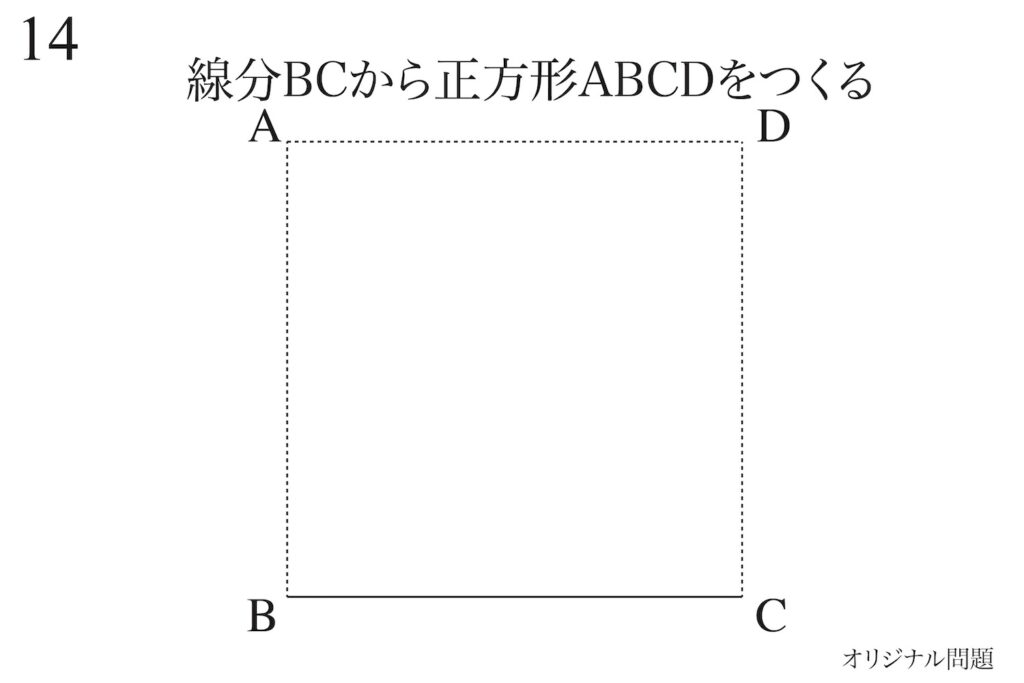
上の辺BCから正方形ABCDを作ってみましょう。
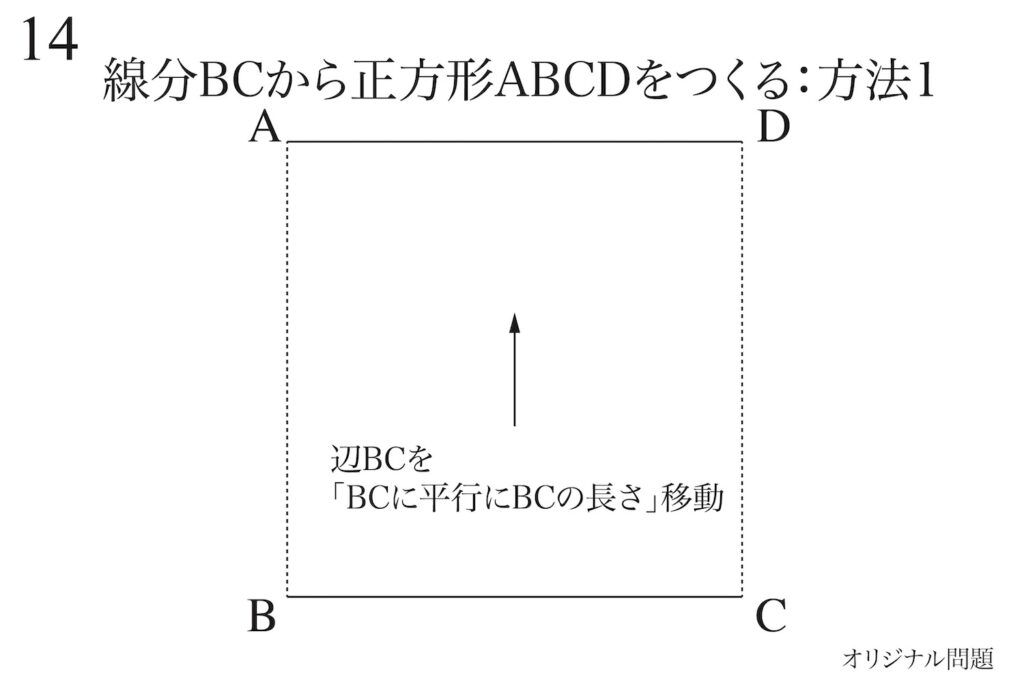
一辺を「その辺と同じ長さ」平行移動すれば、正方形を作ることができます。
別の方法で正方形ABCDを作ってみましょう。
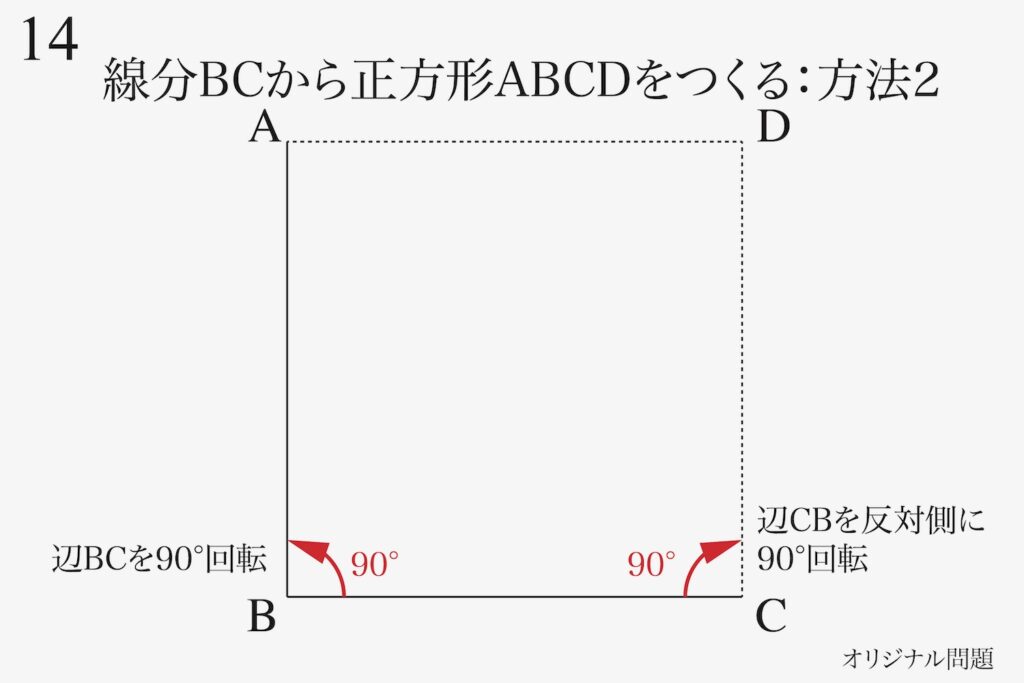
男子小学生これは
分かるけど・・・
ここで、少し考えてみましょう。
「問題をたくさん解く」のも大事かもしれません。
一方で「しっかり理解する」姿勢を身につけるのも大事です。
「問題の考え方」をしっかり身につける姿勢を身につけると、受験期中盤から学力が飛躍的に上がるでしょう。
次回は下記リンクです。
