前回は「3つの食塩水を「混ぜる」がわかるコツ・ポイント〜3つの重さがある「てんびん」・計算は出来るだけ簡単にする・約数を考えて計算ミスを減らす・大小関係は大まかに考える・問題 12解法〜」の話でした。
問題 13
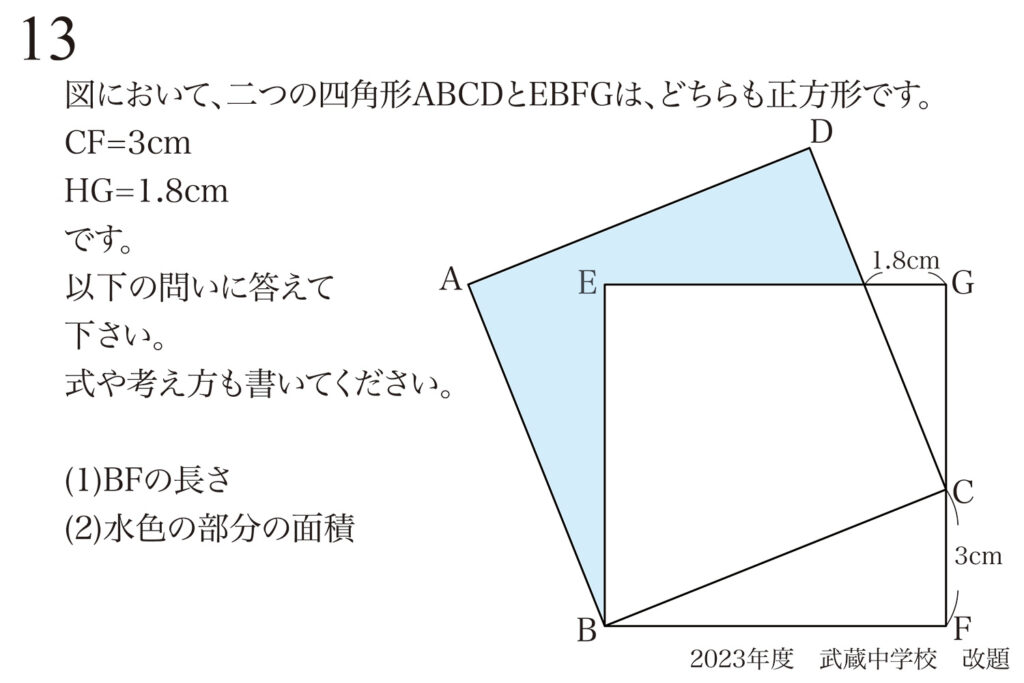
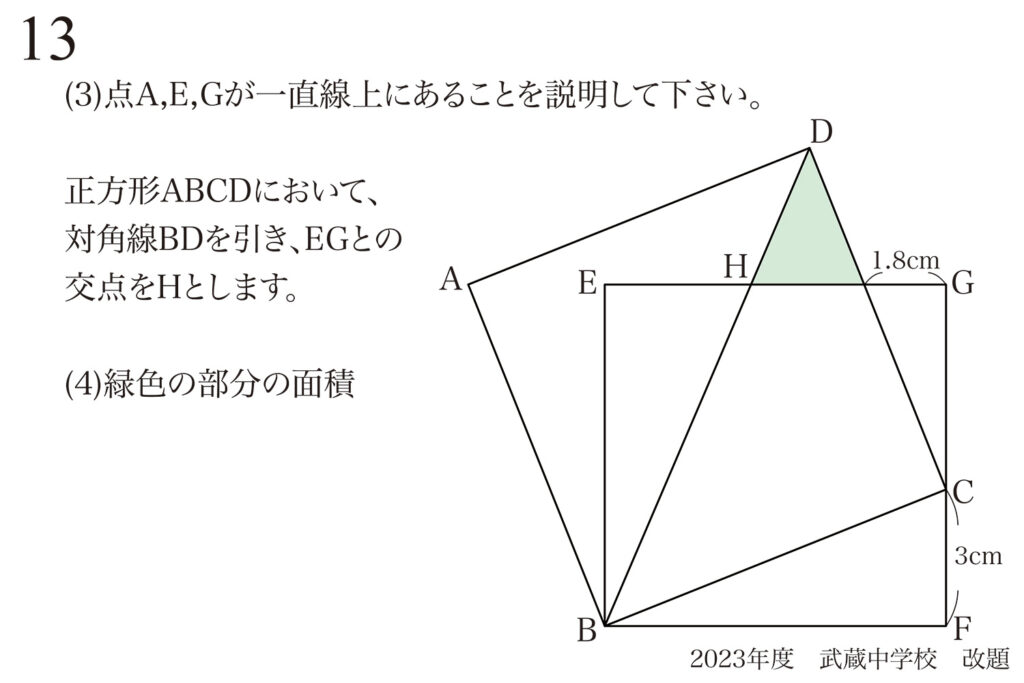
早めに過去問と入試問題と向き合う大事さ
早めに過去問・入試問題をやってみると「目標が具体的になる」効果があります。
2階には一気に上がれないので、階段を登ってゆく話を上記リンクでご紹介しています。
ここで、「3mほどの一気にジャンプできない高さ」を分割して20cm(200mm)くらいに分けます。
すると、大体「階段一段の高さ」となるので、小さな子どもも上がることが可能です。
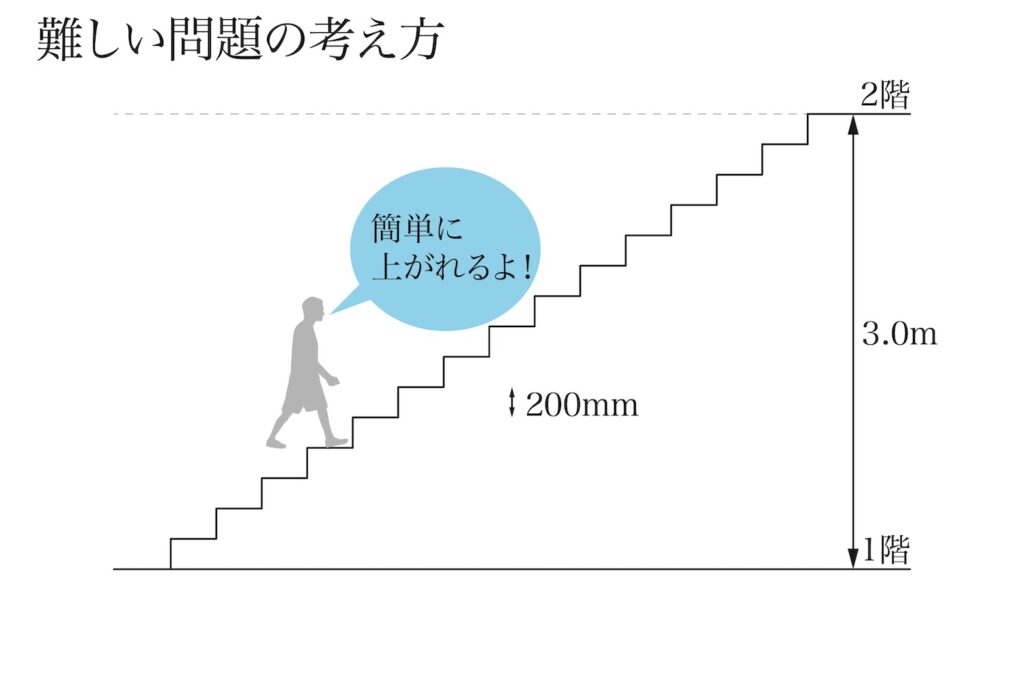
ここで、「2階に上ろうと考えないと、2階には行かない」のが現実です。
本当は「2階に上がらなければならない」のに、1階で右往左往する方もいるかもしれません。
過去問は「出来るか出来ないかをチェックする」ための問題ではなく、「学力を上げるため」の問題です。
特に算数は、早めにどんどんやってみましょう。
 男子小学生
男子小学生まだ、
算数は分からないところが多いけど・・・
そういう方も多いと思いますが、「どういう問題が実際に出るか」を知ることは大事です。
目標を理解して合格へ大きく前進


多くの家庭にはパナソニックの製品があります。



なんとしても2階へ上がりたい・・・
どうしても2階へ上がろう・・・



この熱意がハシゴを思いつかせ、
階段をつくり上げる!



「上がっても上がらなくても」と考えている人の頭からは、
決してハシゴは生まれない。
松下幸之助氏がこのように言っている通り、「なんとしても上がる」という意志が大事です。
同様に受験生の皆さんは「なんとしても合格する!」という強い意志を持ちましょう。
その強い意志を「合格」という形に具体化するためには、「問題を解く力」を上げる必要があります。
過去問は早期に取り組むことには多くの効果があります。
・志望校合格の具体的目標が分かる
・「どのような問題が解けるようになればよいか」を理解
図形問題を得意になるコツ・ポイント:図形の性質を理解
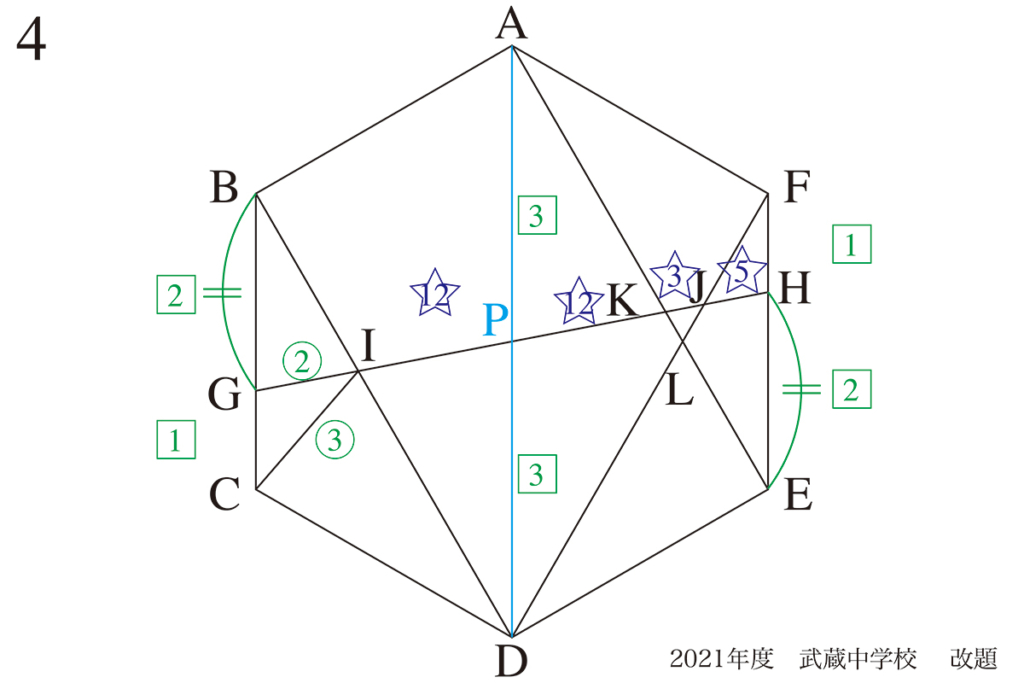

武蔵中学の図形問題は正方形・正〜角形がよく出題されます。
今年は正方形の問題で見慣れた問題ですが、正方形の性質が問われています。
算数・数学、理科は「自分で描くこと」が非常に大事である話を、上記リンクでご紹介しています。
特に図形問題は、「自分で問題の図形を描いてみて、補助線も考えてみる」ようにしましょう。
コツも大事ですが、「描いているうちに分かること」があります。
このような「描いているうちに分かること」は、教えてもらって分かることではないことがあります。
受験生それぞれの個性や学力によるので、なかなか「教える」のは難しく「教わる」のも難しいです。
描いているうちに、



あっ、こういう
ことなのかな?
「自分で気づくこと」があると、それはとても大事な算数の力になるでしょう。
このように正方形・正〜角形のような問題を解くときは、それらの図形の基本的性質を復習しましょう。
・全ての辺が同じ長さ
・全ての角が同じで直角
そのように「図形の性質を学びながら解く」と問題を解く効果が大きく上がるでしょう。
「1を聞いて10を知る」という言葉があります。
実際に「1を聞いて10を知る」は非常に難しいですが、「1を聞いて2を知る」でも十分です。
「1を聞いて2を知る」は「1を学んで、2倍学ぶ」ことになります。
このような姿勢で勉強すると、「1題学んだ力」が2題分あるいは3題分になるでしょう。
「たくさんの問題を解く」のも良いですが、このように「多くを学ぶ姿勢」を身につけましょう。
難関校〜最難関校の難問・応用問題を解く力も大きく増強するでしょう。
次回は下記リンクです。





