前回は「算数の学力の伸ばし方〜同じように考える姿勢・大事なポイントを意識して学力アップ・横断的に考える視点・問題ごとの解法ではなく大事な「共通する考え方」・様々な図形と様々な解き方〜」の話でした。
算数の学力停滞と突破する「きっかけ」
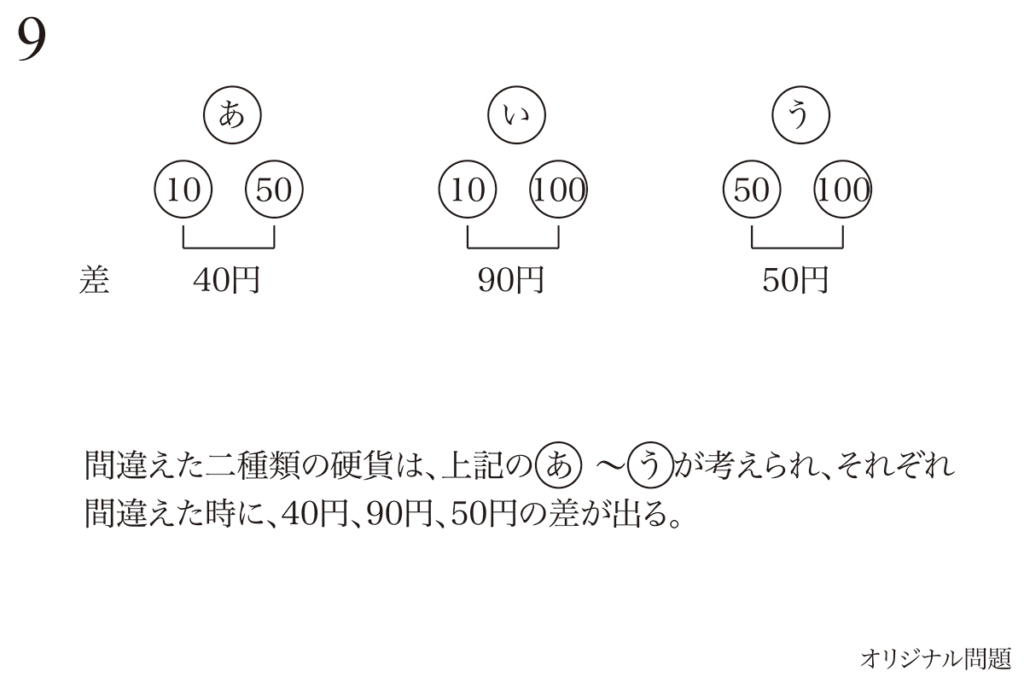
一月ほど前、大学時代の同級生から連絡があり、
うちの息子が御三家の
K中学受験するんだ・・・
成績は結構安定して良くて、
算数と理科が得意なんだ・・・
成績が安定して良くて、しかも算数と理科が得意だったら、どこの中学校でも合格できそうです。
ところが、得意だった算数が
ちょっと最近思わしくなくて・・・
結構点数も偏差値も高かったのに、
低下傾向にあるんだ・・・
それで、本人も自信を無くしてしまっていて
困っている・・・
算数・数学は最もスランプに陥りやすい傾向があります。
すまないが、一度本人と会ってやってもらい、
君なりのアドバイスを頂けないだろうか。
大学時代の同級生からの依頼ですから、すぐに快諾しました。
そして、友人のお子さんH君と会って、色々と話をしました。
受験の方向性や志望校選択などの話とは異なり、具体的な「算数の学力」の相談です。
これは、本人と話しただけでは分からないので、最近の模試の答案・ノートなどを見せてもらいました。
模試の考え方・ノートなどを見れば、「どのような考え方で解いているか」が即座にわかります。
うん。これは
かなりの学力をしっかり持っている・・・
友人の言う通り、算数の学力はかなり高い方だと思いました。
ところが、
ここは、ちょっと目標が
ずれてきているかな・・・
「学力がある」だけに、少し「力技に頼ってしまう」傾向が見受けられました。
これは、H君に限った話ではなく、算数・数学が得意な方に「ある程度共通する思考」です。
「算数・数学の学力がある程度つく」と、大抵の問題は「考える最初の方向性が見える」のです。
すると、「学力がある」だけに「力で解く」傾向が出てくることが多いです。
この算数・数学を「力で解く」のは「算数・数学の学力が向上するプロセス」でもあります。
ここはね、
こういう風に考えてみたら・・・
あっそうか。
こう考えると良いんだね！
ケースバイケースですが、「ここはこのようにも考えられる」と言う視点は大事です。
ここなんだけどね・・・
似た問題でも、いつもつまずいて・・・
こういう問題は、
こう考えてみたら・・・
なるほど・・・
良く分かります・・・
そして、こう考えることも
出来るよね・・・
そっかあ・・・
少し違いますね・・・
このような感じで、一通り「困っている」点に関して、僕なりにアドバイスしました。
なんか、色々と
分かった気がします！
有難う
御座いました！
喜んで帰っていったH君。
算数の成績が上がると
いいな・・・
と思いました。
そして、ひと月ほどのちになって、友人から電話がありました。
先日は有難う！
実は息子の成績がだいぶ上がった！
嬉しい知らせです。
何かちょっとしたコツがあったみたいで、
成績が良くなって、自信も出てきた！
「成績が上がり、自信が出る」ことは、受験においては最重要です。
息子が君から教えてもらったことは、
とても良かった！
有難う！
まさに「仙豆」みたいな効果があったよ！
「仙豆」みたいな効果と言われることは、僕たちの世代にとっては嬉しいことです。
今の子どもたちは知らないかもしれない「仙豆」。
ドラゴンボールで「仙豆を食べる」と「傷ついた体が完全に復活」します。
「ドラゴンクエストのベホマ」のような仙豆ほどの効果があったことは、大変嬉しいことでした。
算数の学力の飛躍的にアップする勉強法：着実に答えに近づいてゆく姿勢
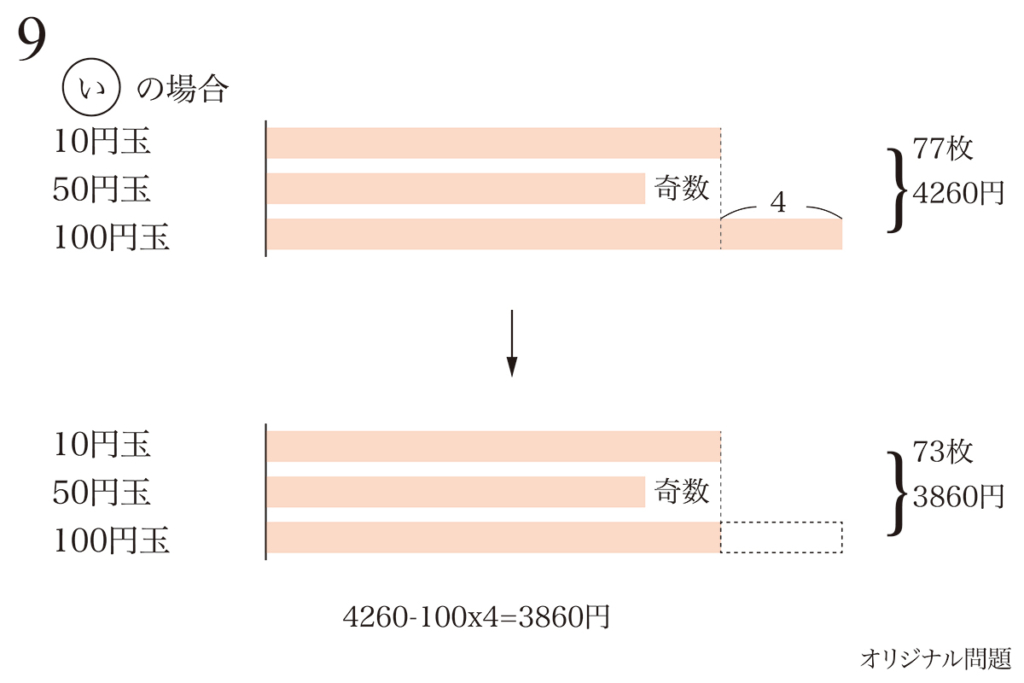
文章題でも図形問題でも、難問は「すぐに解ける」ことは少ないです。
「問題を解く」ためには、その前に「分かりたいこと」を見つけて、それを考えることが大事です。
文章題では、様々なシチュエーション・状況が設定されます。
大事なポイントは類似していますが、このシチュエーション・状況設定こそが、問題を作る肝です。
この問題は、
ここがポイントなんだけど・・・
それが気づきにくいように、
状況をこう設定して、少し複雑に・・・
と問題作成者は考えているのでしょう。
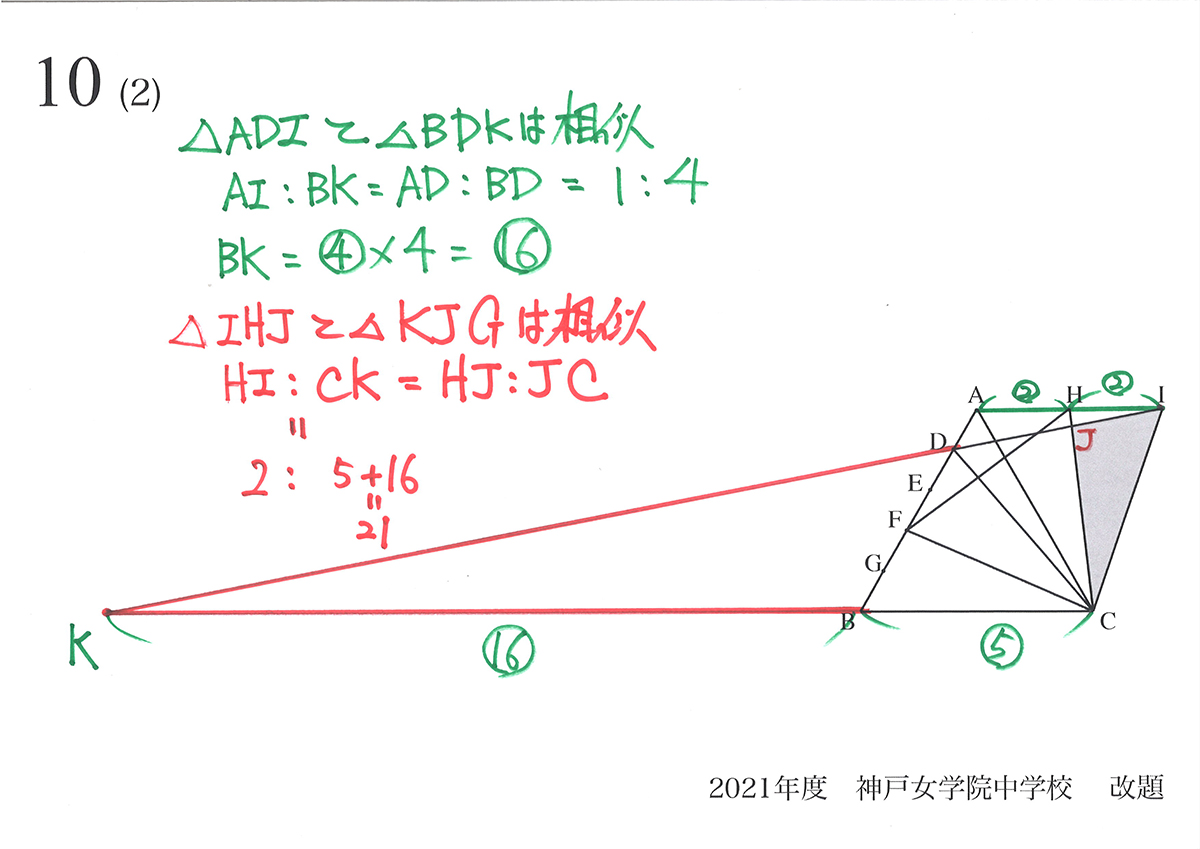
文章題も図形問題も「何かを知るために、まず何かを知る」という目標を明確にすることが大事です。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
「相似形を見つける・つくる」ことが出来れば、大抵は解ける図形問題。
・「相似形が必ずある」と考えて、相似形を探す
・相似形が見つからないときは、「相似形を作って考える」姿勢
面積や比を求めるときは、「関連する辺の比」をしっかりと目標に定める姿勢が大事です。
・平行な線、相似形を探す・つくる
・相似比となる「対応する辺」の長さを計算
・「対応する辺の長さ」が分かりにくい時は、辺を分割して考える
ドンドン進まずに「周りを見渡しながら」解く
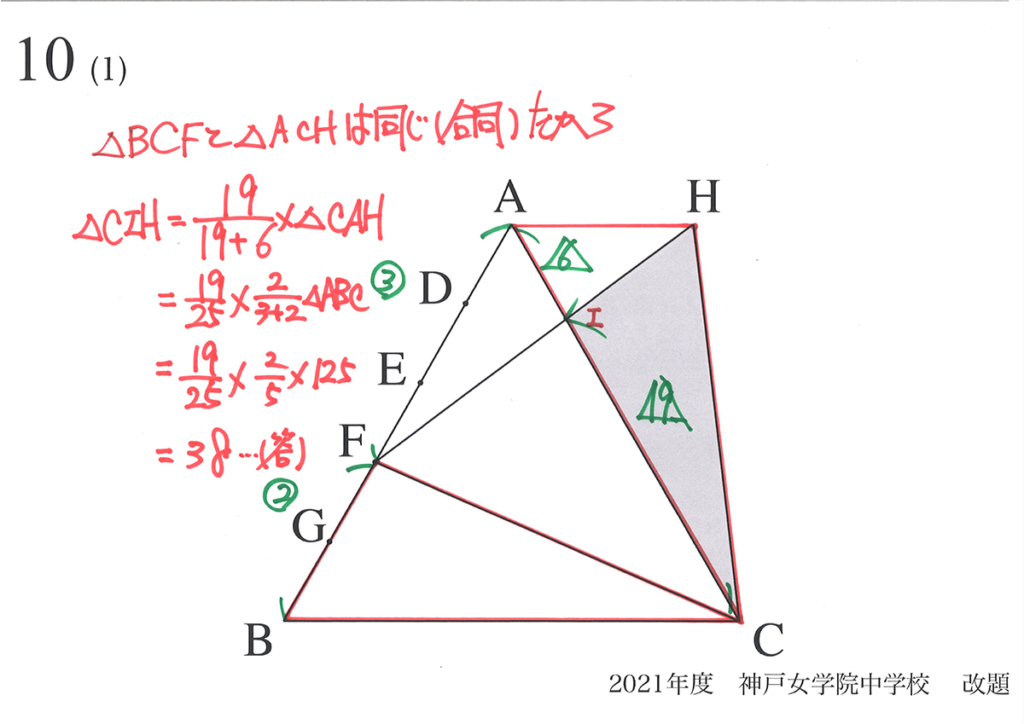
「目標を定めることが大事」なのは当然です。
ところが、算数・数学がある程度出来る方は、「ここがブレてしまう」傾向があります。
それは「力があるからこそ、ドンドン進んでしまう」からです。
これは、
こう解くんだ！
学力があるために、問題をみたら「ドンドン手が動いてしまう」のです。
すると、例えば「小問が3つくらいある」問題では、
(1)はすぐ解けるけど、
(2)がちょっと解らない・・・
あるいは、(2)までは調子良く進んで「(3)で手が止まってしまう」などあります。
「解く＝目標は何か」を明確に意識する事が大事です。
・「求めるもの」は何かを明確に意識する
・簡単な絵や図を描いて、状況を理解する
・「分かりにくい」時は、「周囲を見渡す」イメージで違う角度から考える
特に秋以降は、難関校〜最難関校を目指す方は、算数で「なにを、どう考えるか」を明確にしましょう。
ひたすら「数多くの問題を解く」よりも、「じっくり考える姿勢」が大事です。
すると、これまで学んできたことが「有機的ににつながってゆく」でしょう。
そして、様々な問題を解く力が「確固たる応用力」に成長してゆくでしょう。