前回は「動く点と図形を理解するポイント〜新たに出来る正方形の特徴・図形の特徴を探る姿勢・直線と角度に注目・正方形の作り方・平行移動と90度回転・矢印の考え方・問題14(2)(3)解法〜」の話でした。
問題14(1)(2)(3)(再掲載)
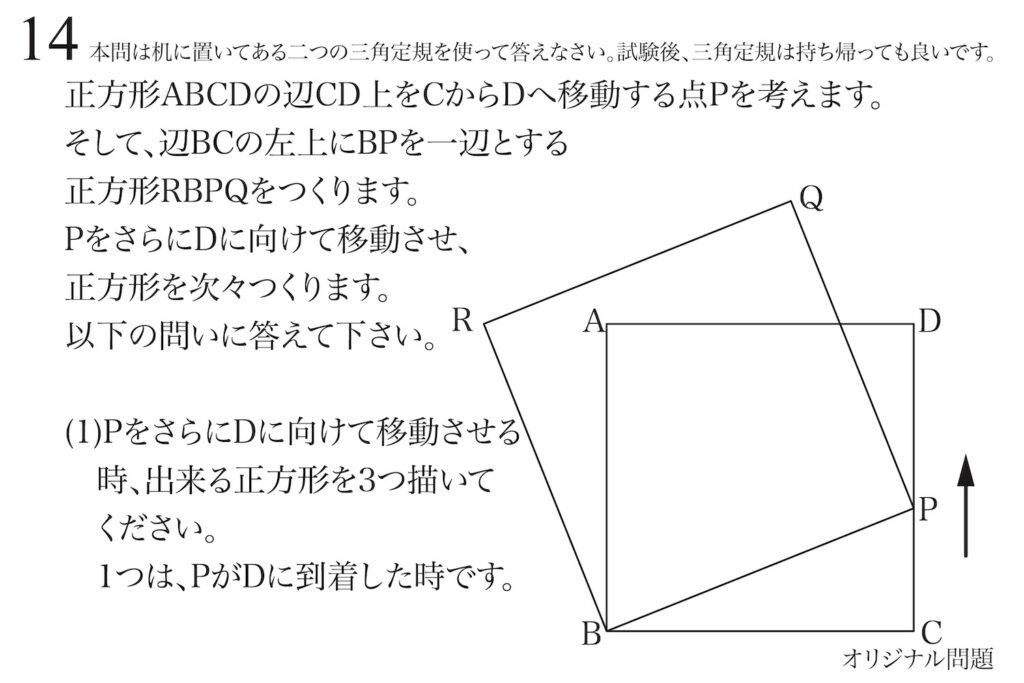
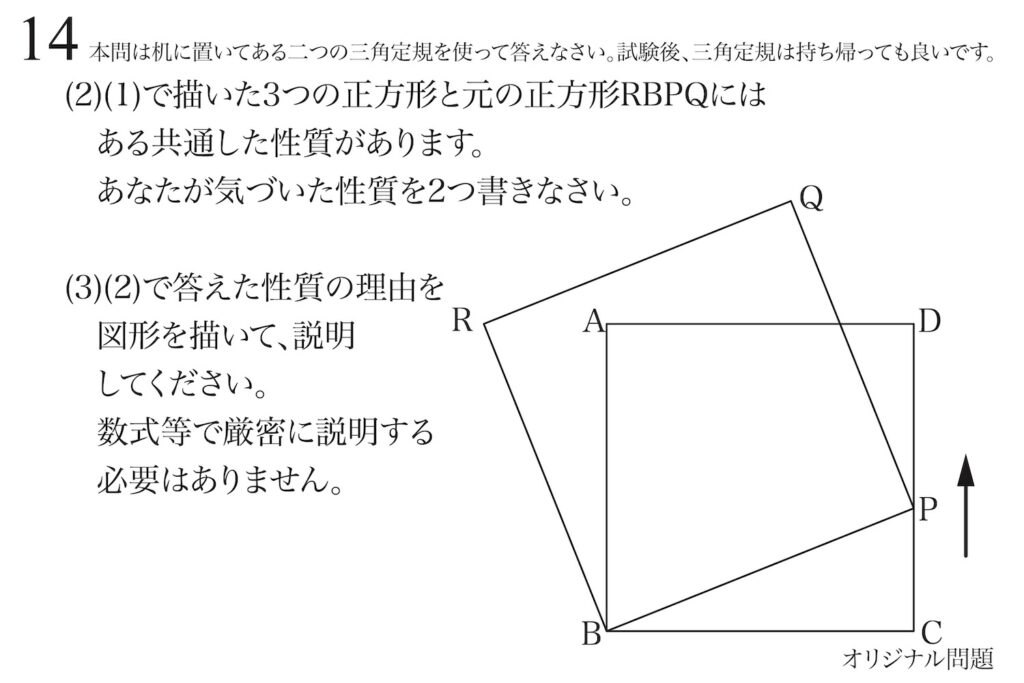
動く点・動点と新たに出来る正方形の性質
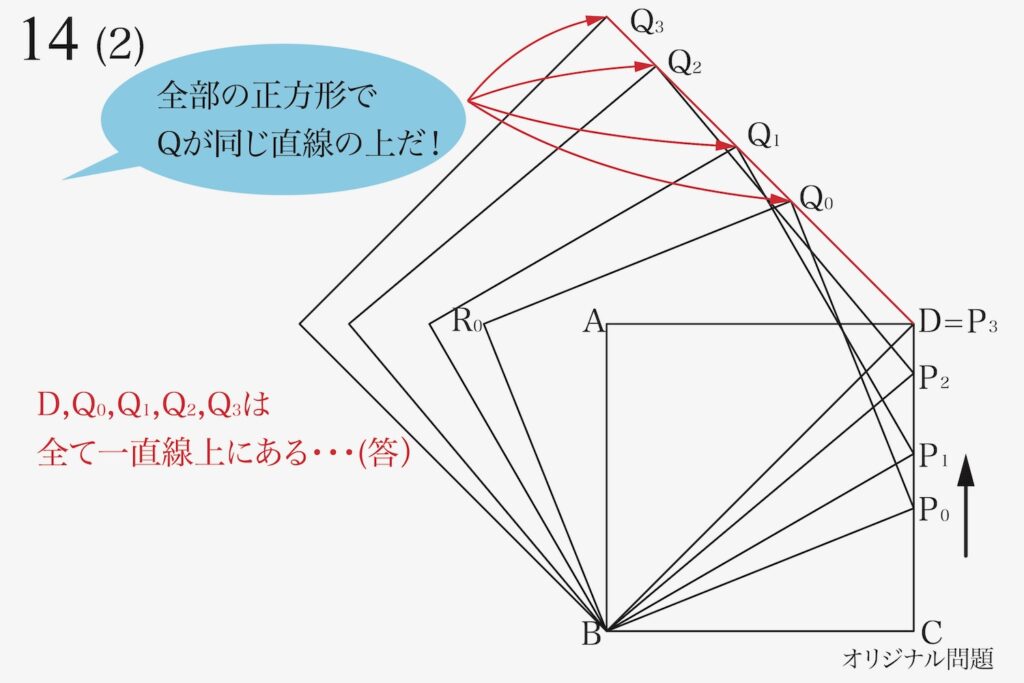
もともとある正方形ABCDの辺CDを動く点Pと共に、新たに正方形R0BP0Q0が出来ます。
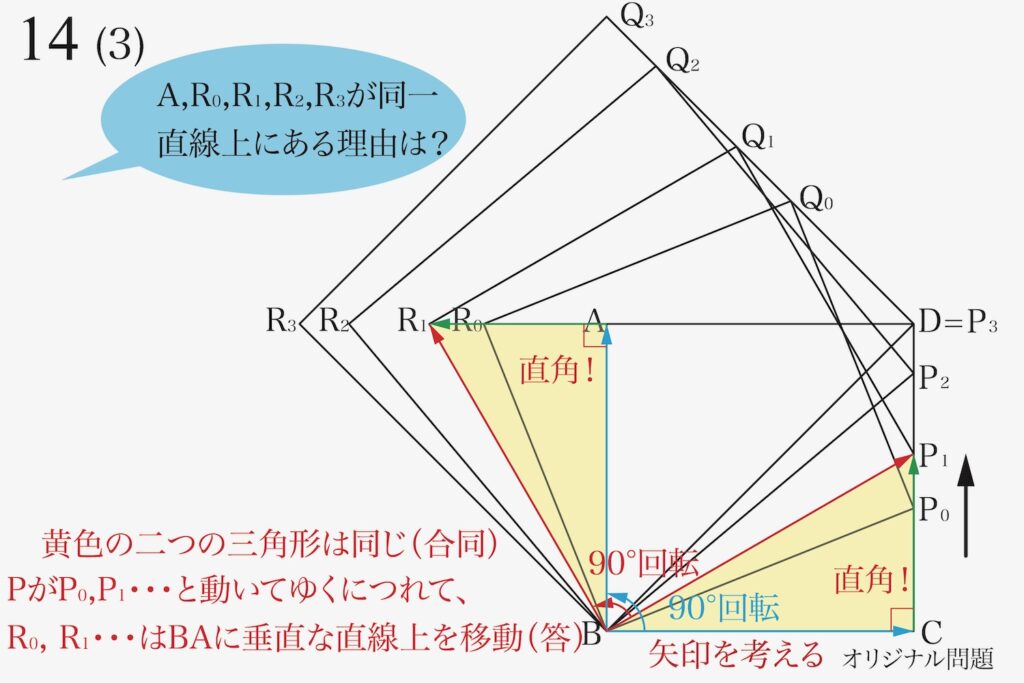
それらの正方形R0BP0Q0に「共通する性質」二つに気付きました。
・点D、Q0、Q1、Q2、Q3は全て(同一)の一直線上にある
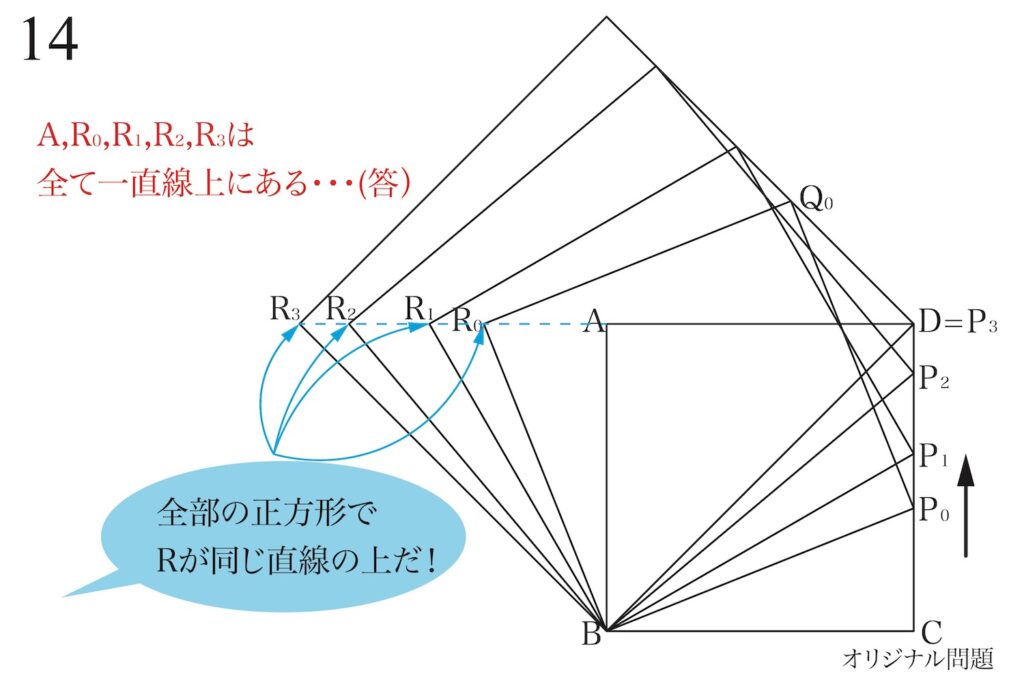
・点A、点R0、R1、R2、R3は全て(同一)の一直線上にある
今回の問題の主役である正方形には大事な性質があります。
・全ての辺が同じ長さ
・全ての角が同じで直角
前回は「矢印」を考えて、二つの性質のうち一方の性質が成立することを図形的に説明しました。
正方形・正三角形など、正〜角形にはたくさんの性質があります。

方眼紙の基本単位・セルでもある正方形は、非常に大事な図形です。
非常に大事で、非常に身近な正方形の性質は、しっかり復習して理解しておきましょう。
仲間の点同士と線同士を探す姿勢:同じ図形と相似形を探す
・共通する性質の点が同じ(同一)の直線上にある(直線は見えない場合がある)
・共通する性質の点が同じ(同一)の方向・角度を向いている
「なんらかの性質がある」時は、「同じ直線上にある」ことは一つのポイントです。
図形の問題で「何か性質を探す」時は、
 男子小学生
男子小学生ある点同士が、
何かの共通の直線の上にないかな?
このように「共通の性質」を探すと良いでしょう。
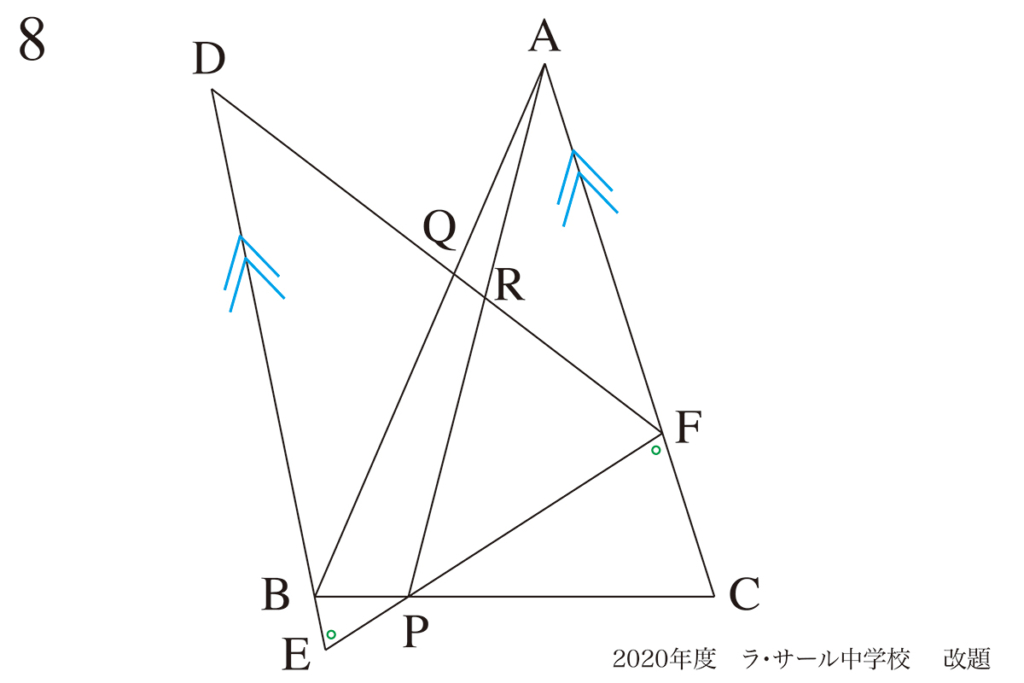

「何かの点が同一直線上」を探すのは、「何かの辺が平行」であることを探す姿勢に似た面があります。
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
ある点同士が「同一直線上にある」や「ある線同士が平行」という性質は、それらが「同じグループ」です。
つまり、「点同士・線同士がお友達」であるイメージを持ちましょう。



確かに
「同じグループ・友達」って考えられるね!
そして「仲間・友達同士の点・線を見つける・つくる」ことが大事です。
すると「同じ図形・相似形を見つける・つくる」姿勢につながり、図形攻略のポイントになります。
・仲間・友達同士の点・線を見つける・つくる
・同じ図形・相似形を見つける・つくる
新たに出来る正方形の軌跡を追いかける
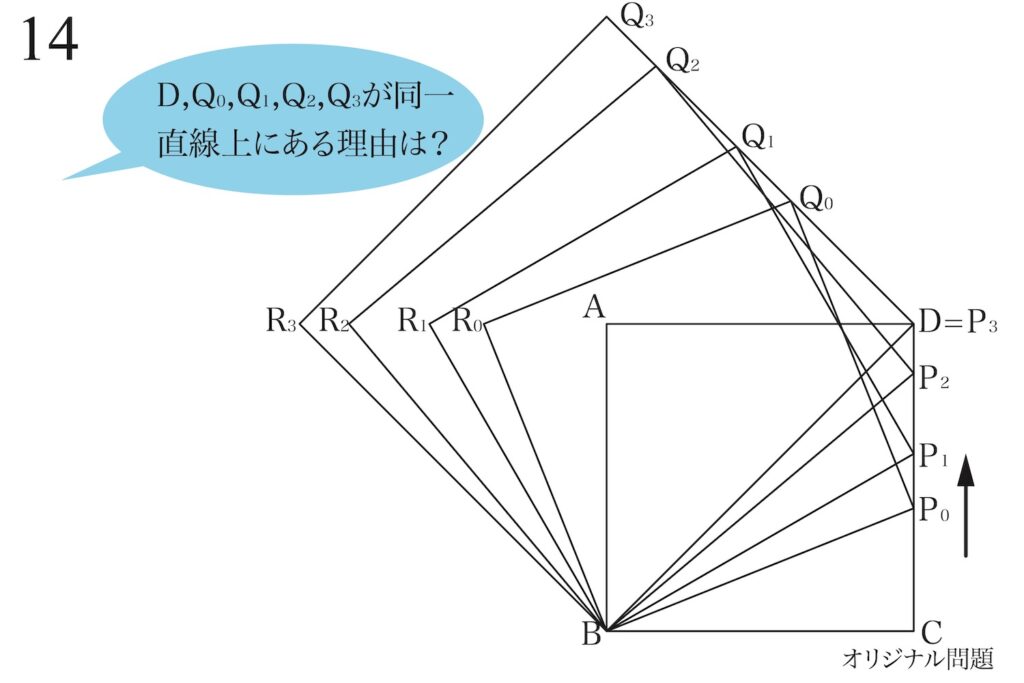

今回は、(2)の答えの前半部を説明することを考えます。
・「点D、Q0、Q1、Q2、Q3は全て(同一)の一直線上にある」説明←今回はこちらを考える
・「点A、点R0、R1、R2、R3は全て(同一)の一直線上にある」説明←前回はこちらを説明
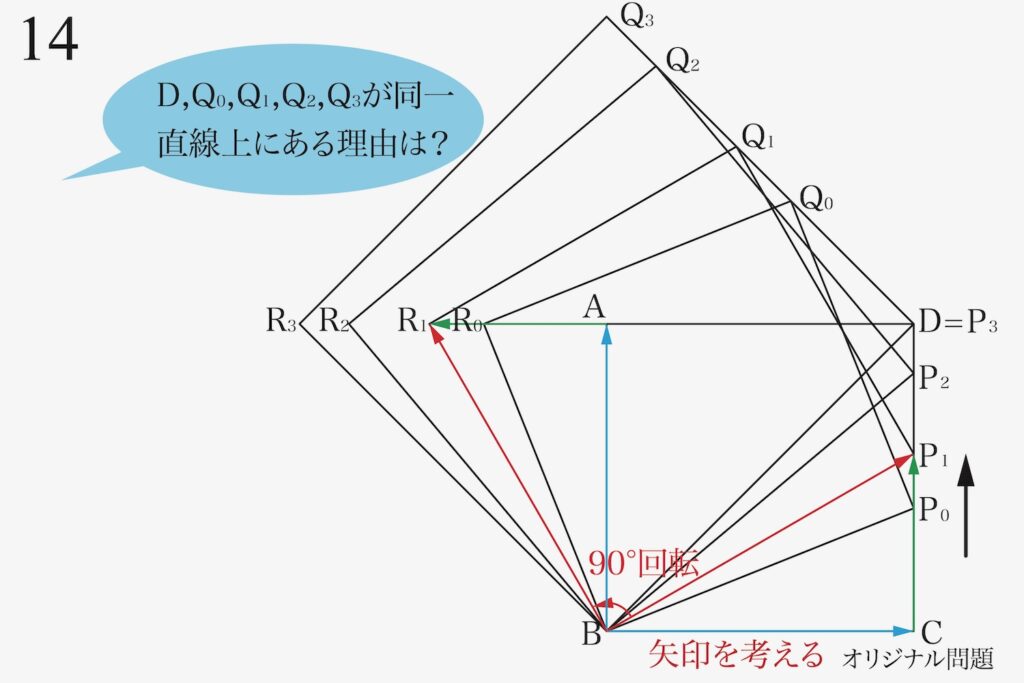

前回と同様にBP1を基準に、「どのように正方形R1BP1Q1」が出来るかを矢印で考えましょう。
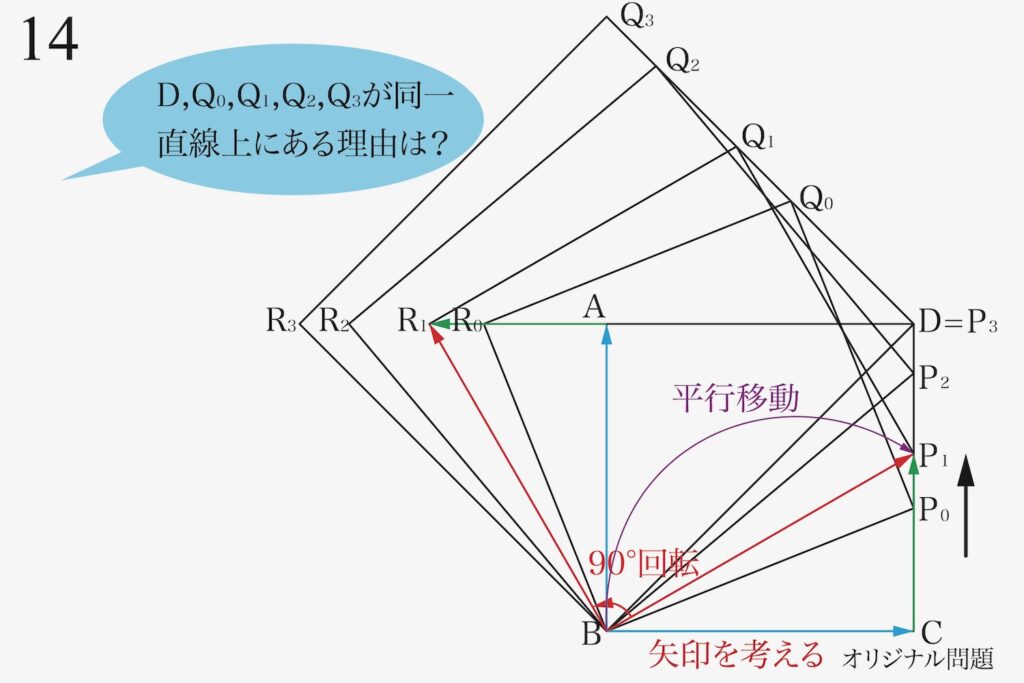

今回は「Q1の動き」を知りたいので、「BR1を平行移動して、P1Q1をつくる」を考えます。
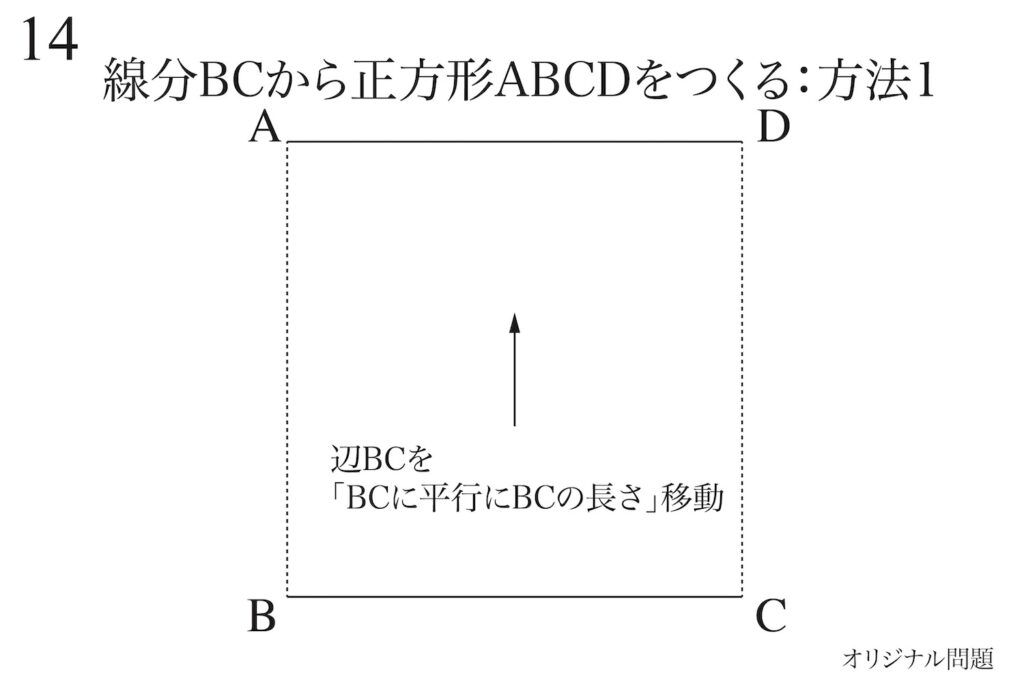

正方形をつくる一つの方法は「ある辺をある辺と平行にある辺の長さ」移動すればできます。
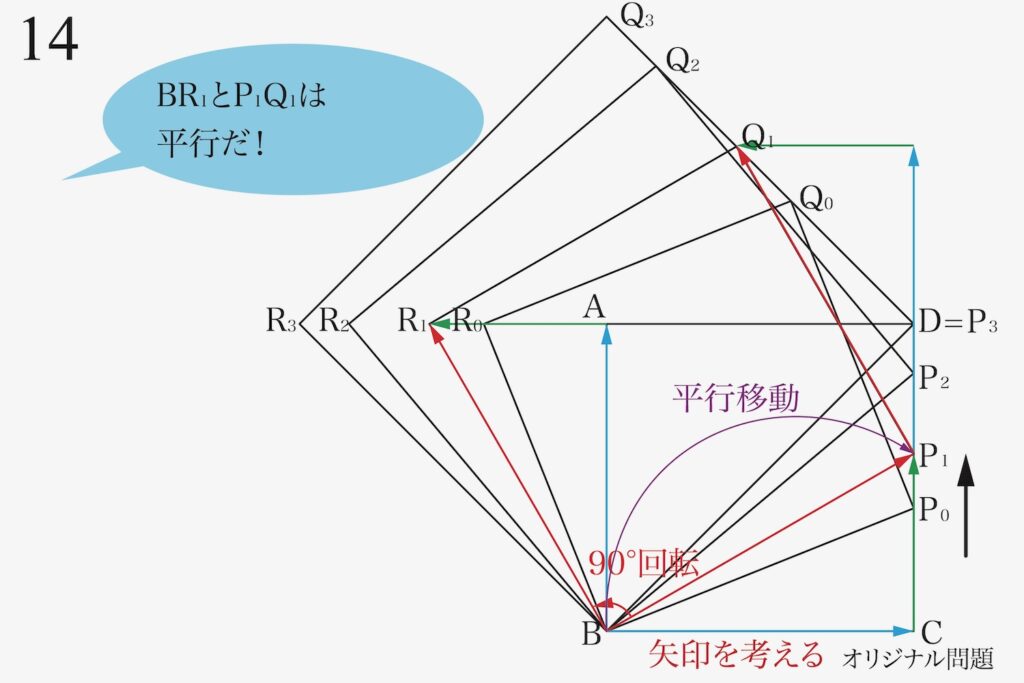

基準となる△BCP1を矢印で考えた図形を「90度回転させて、平行移動」させます。
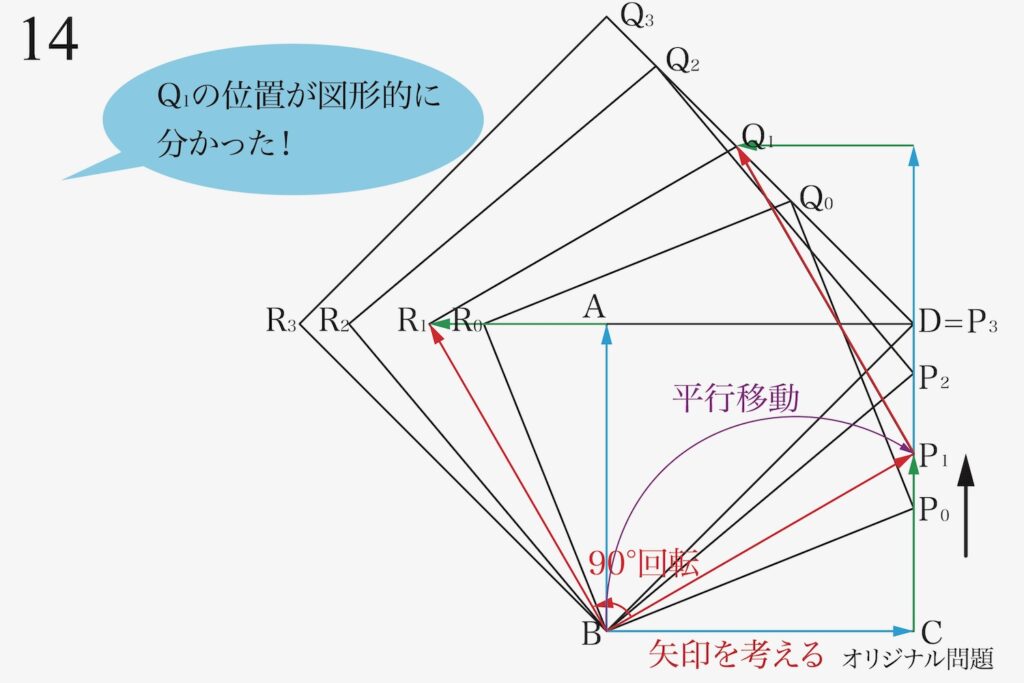

これで、Q1の位置がわかりました。
これで
説明出来たかな?
まだ、これでは
「D,Q0,Q1・・・が一直線上」は説明出来てないんじゃない?
確かに
「一直線上」は説明できてないね・・・
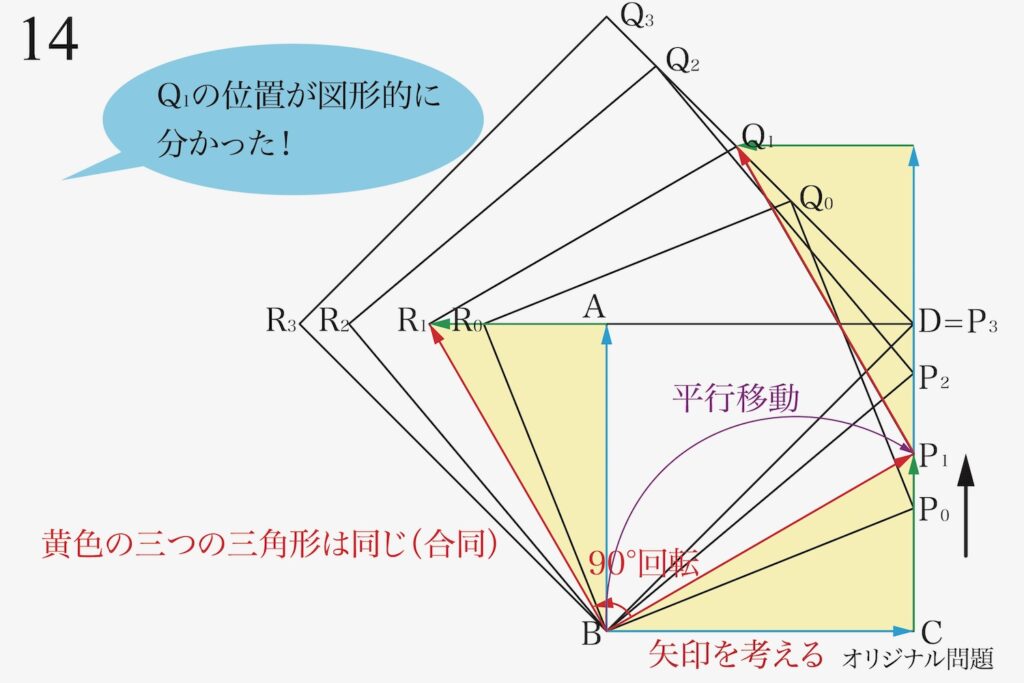

あっ、でもさあ、
上の図で三つの黄色の三角形は同じだよ!
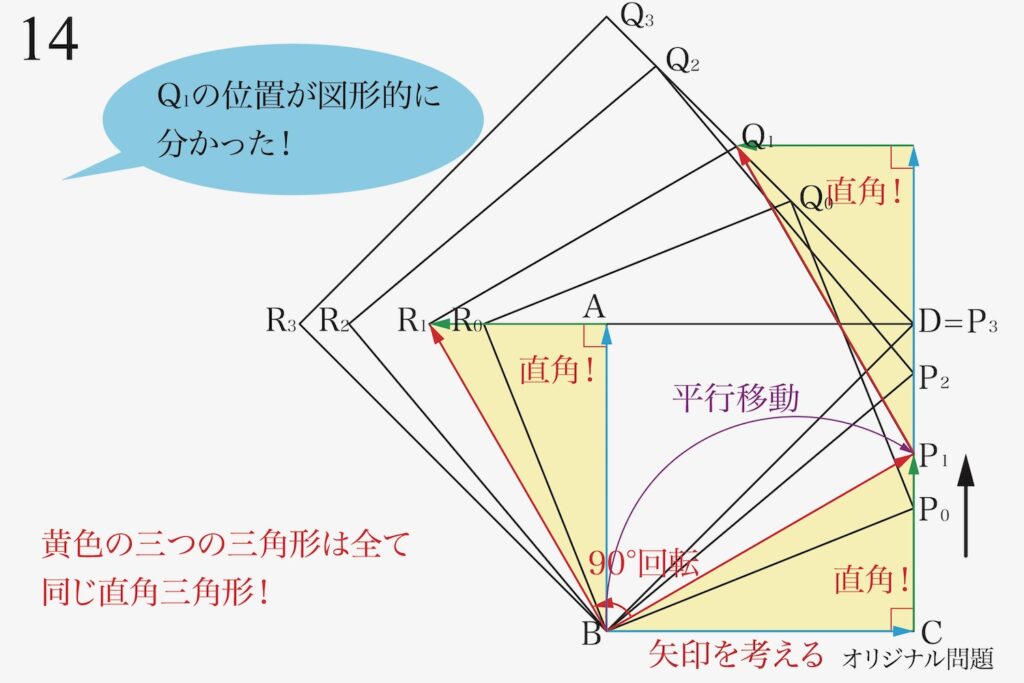

三つの黄色の三角形は全て同じ「直角三角形」であることが分かります。
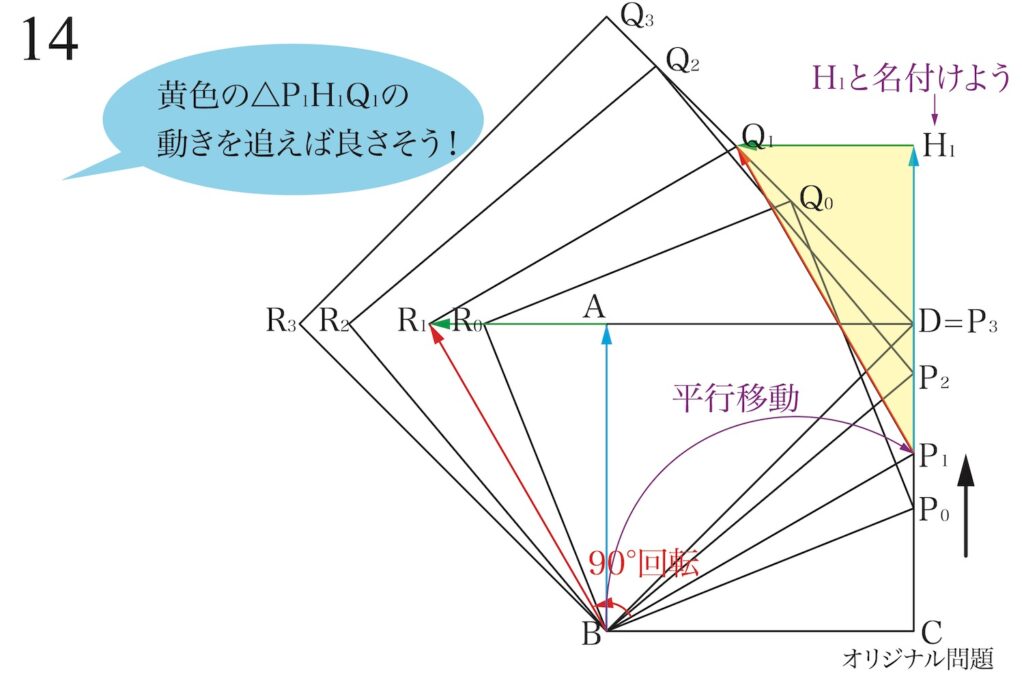

ここで、新たに出来た直角三角形の直角部分の点に名前をつけます。
ここでは「H1」としますが、好きな名前で良いです。
他のP1,Q1,R1と同様にH1も「Pの動きに合わせて、H0,H2・・・」とできるイメージです。
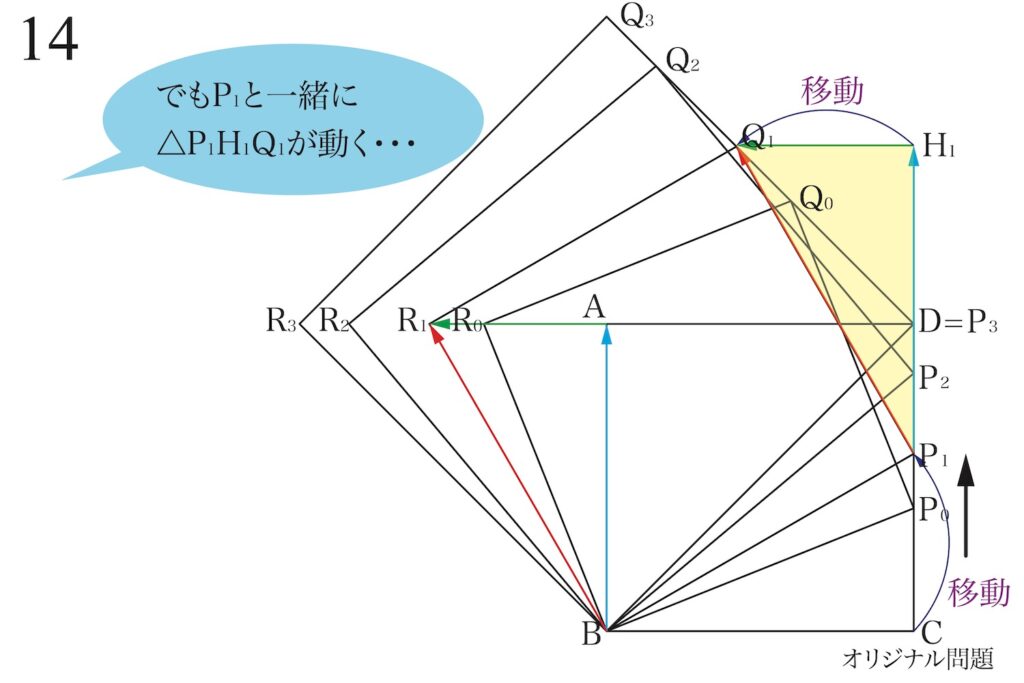




分かりそうだけど、
P1と一緒に△P1H1Q1が動くね・・・



これでは、
点Q1の位置が分からないね・・・
動く点・動点の軌跡のポイント:「固定の点」を基準に考える
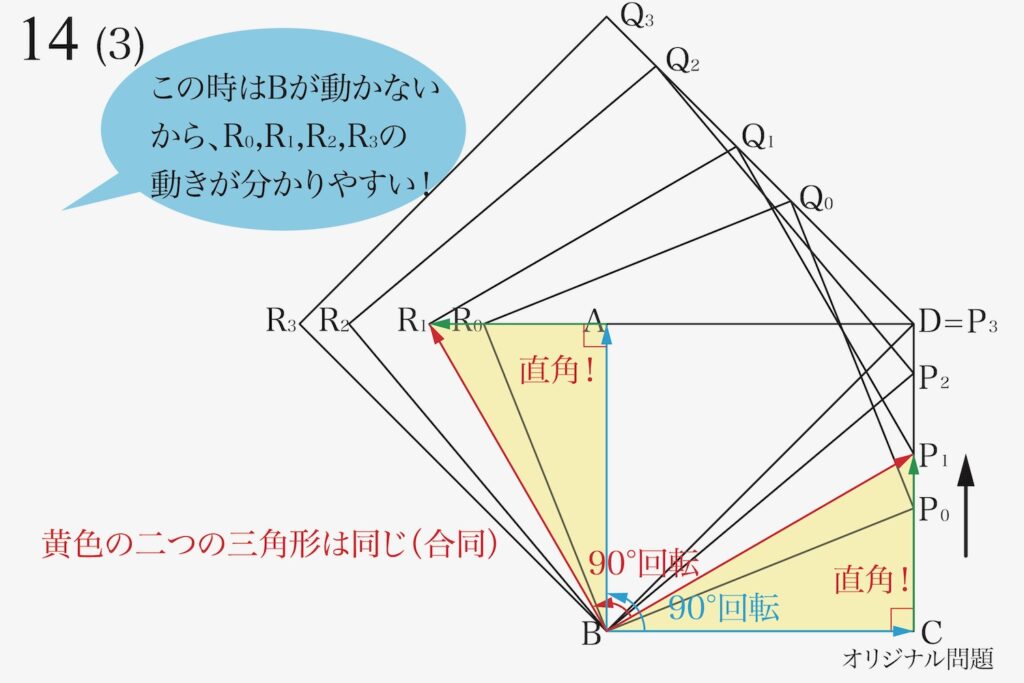

前回「点R0,R1・・・」の動きを追いかけた時を考えましょう。
この時、分かりやすかった理由があります。



点Bがいつも同じ位置だから、
分かるんだね!
この時は、「点R0,R1・・・」を「追いかける基準となる点Bが固定」であることがポイントでした。
そこで、今回は「動く点が基準」なので「固定の点を基準」にするように考えましょう。
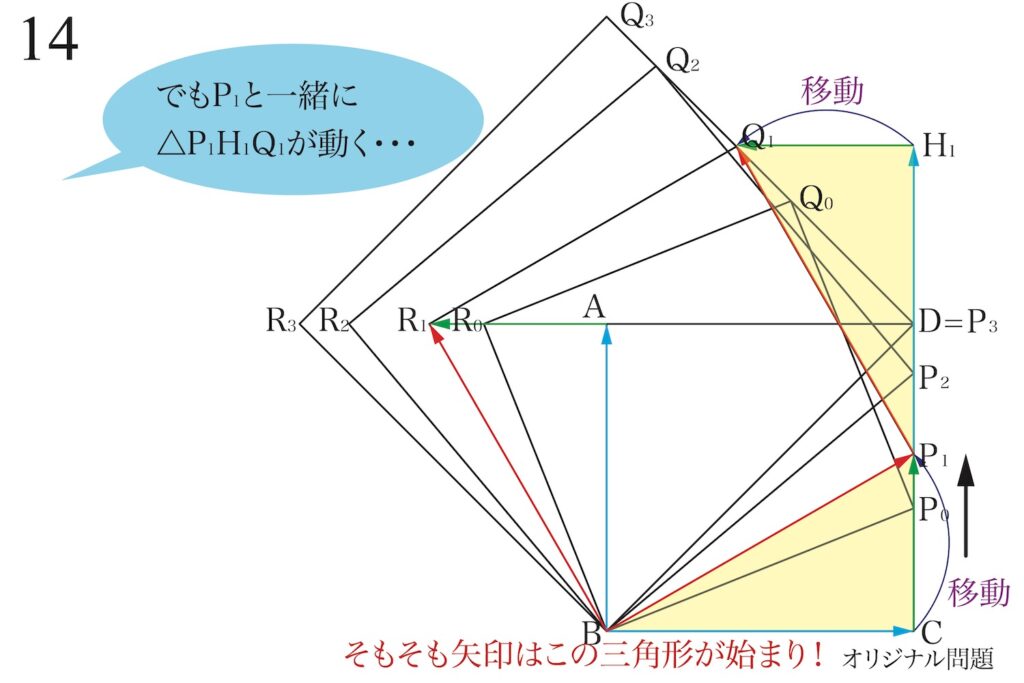

もう一度「そもそも矢印の三角形」を考えましょう。
そして、動く点PがP0,P1,P2・・・と動く様子をイメージして、描いてみましょう。
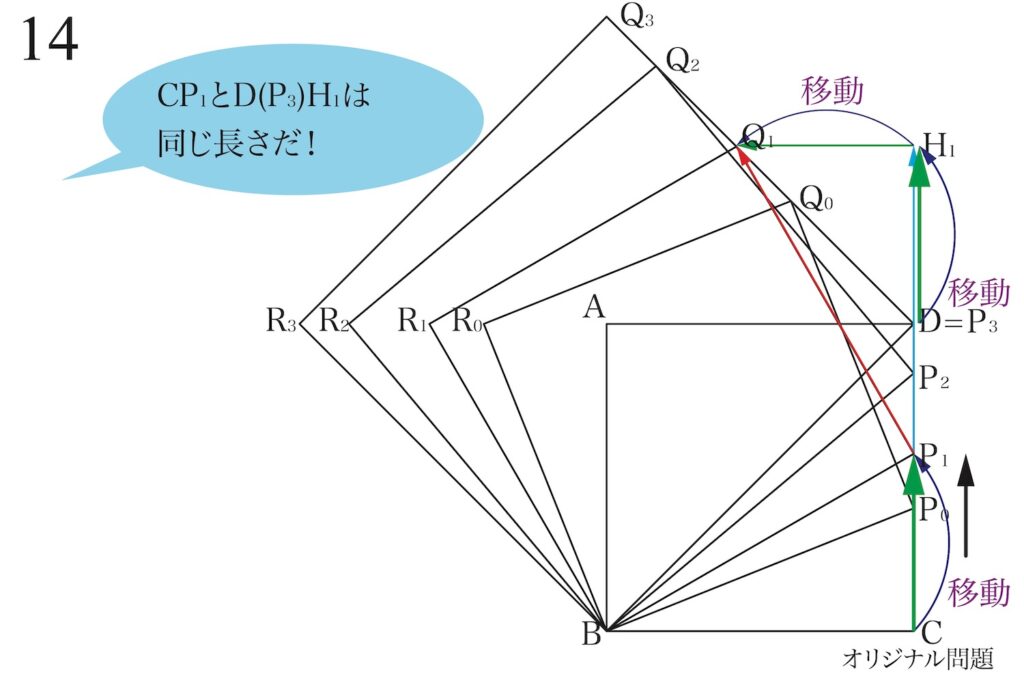

ここで、大事な性質に気づきます。
「CP1とD(P3)H1が同じ長さ」であることです。



これは大事な
性質だね!
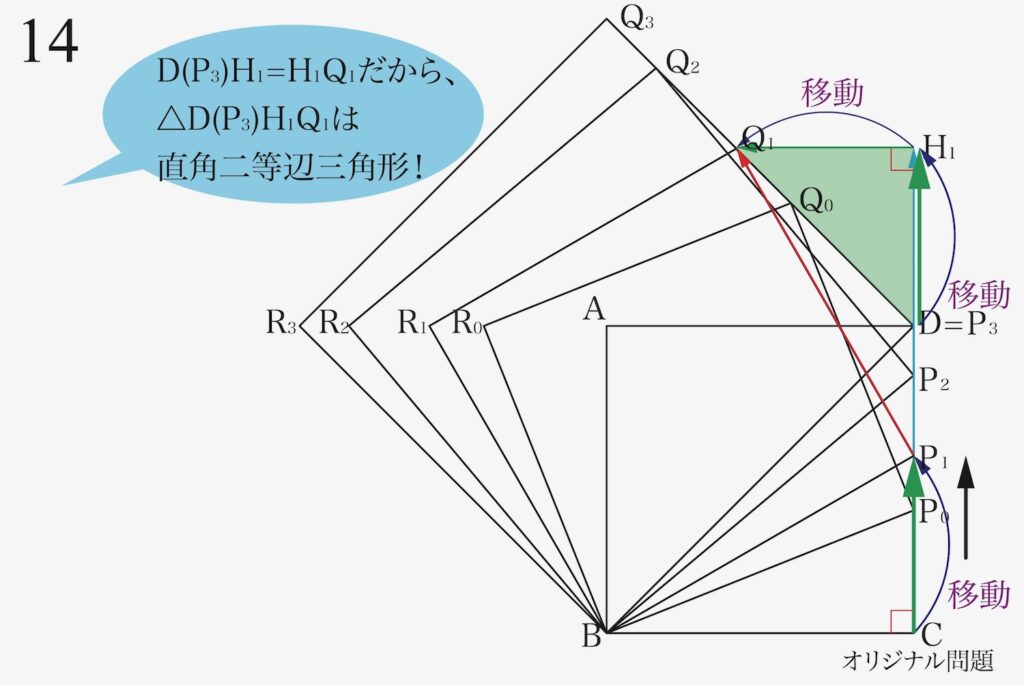

ここで、これまで考えていた「黄色の直角三角形」から、上の緑色の直角三角形を考えます。
黄色の直角三角形は「動く点P1が基準」でしたが、緑色の直角三角形は「固定点Dが基準」です。



緑色の直角三角形は、
直角二等辺三角形だね!



これで、Q1の位置が
固定点Dを基準に分かる!
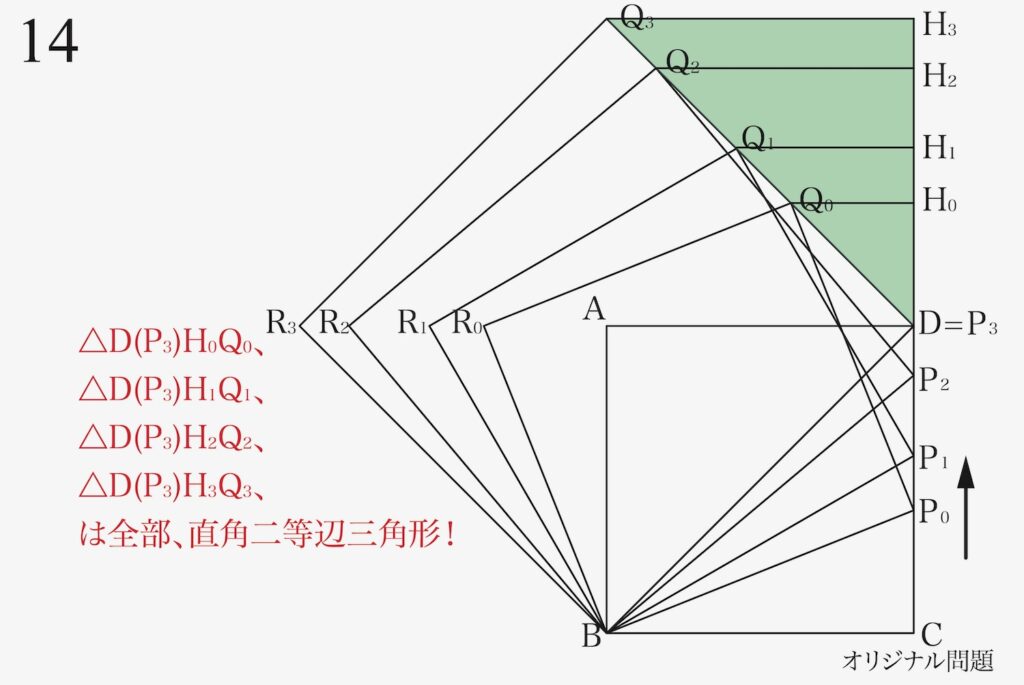

同じように考えると、他の点P2やP3に対応する点Q2,Q3でも同じことが成立します。
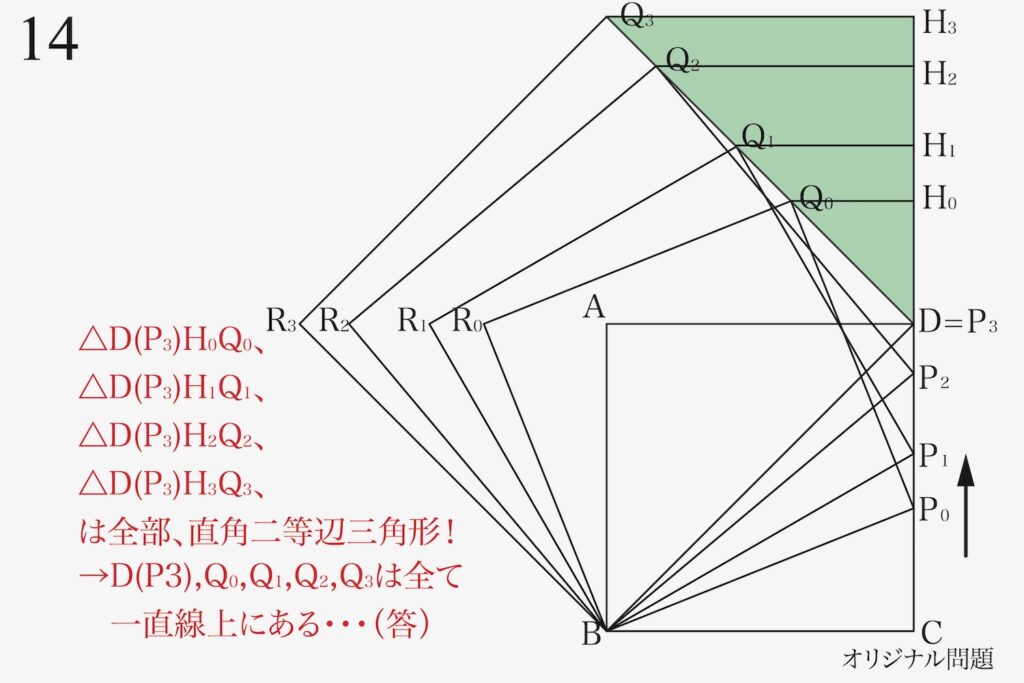

これで、図形的に「点D、Q0、Q1、Q2、Q3は全て(同一)の一直線上にある」が説明出来ました。
・新たに出来る点・図形がどのように出来るか、を考えて描く
・新たに出来る点・図形を、固定点を基準として位置関係を考える
このように動く点・動点は、「固定された点からの位置関係」を考えれば分かります。
「難しいイメージ」の図形の動く点は、基本的性質を押さえて「固定点との関係」を考えましょう。
次回は下記リンクです。



