前回は「相似形の性質と間違えやすいポイント〜テクニックより大事なこと・相似形は「お友達」・相似形の理由・分かる辺の長さを計算・分数と少数の計算のコツ・問題13(4)解法〜」の話でした。
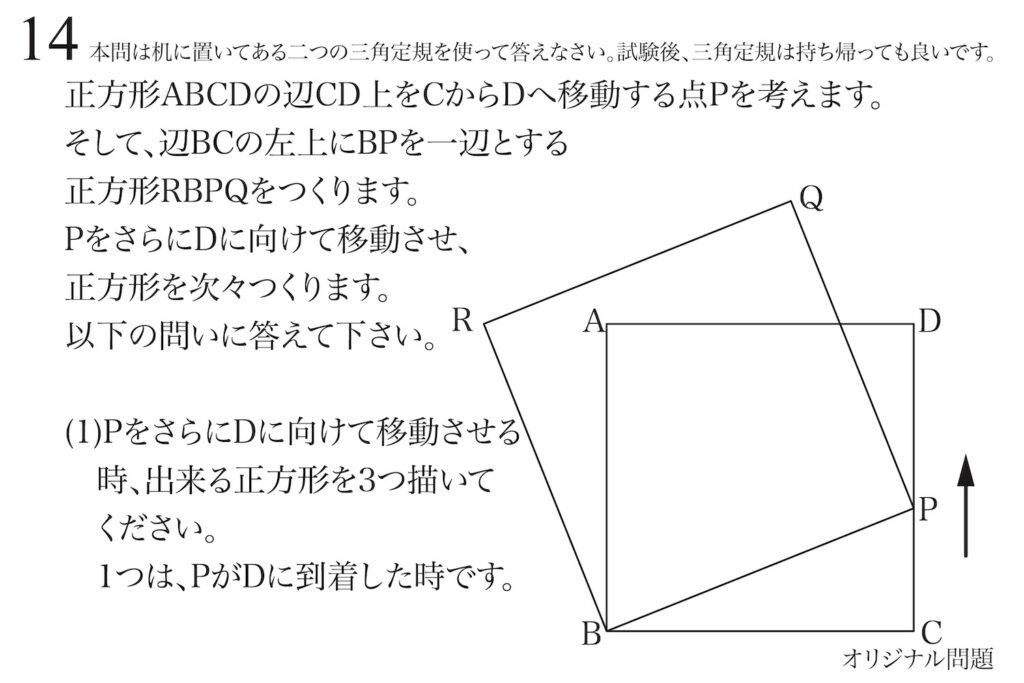
問題14：動く図形を描く
実際に自分で描く姿勢：定規を使って正確に作図
この問題は、問題13から派生したオリジナル問題です。
「面積を求めよ」とか「辺の比を求めよ」という図形問題が多い中、「図形を描きなさい」は、あまり見かけません。
見かけない最も大きな理由は、「試験会場に定規を持ち込むことが前提となっていない」ことがあるでしょう。
基本的に「鉛筆（シャープペンシル）と消しゴム」のみが持ち込み可能である試験場。
ここで、「図形を描いてもらう」試験は、出題しにくいのが現実です。
そこで、今回は「三角定規を学校側が用意して、受験生に使用してもらう」想定で考えています。
武蔵中学では「おみやげ問題」という「理科で、当日出題されたモノ」を持ち帰る問題があります。
それと似た感じで、「使用した三角定規は持ち帰っても良い」という内容にしました。
図形を頭と身体で理解
二つの特徴的な直角三角形である三角定規の組み合わせで、「平行な直線を引く」ことを考えます。
この「平行な直線を引く」のは、小学校中学年くらいで学校で教わる方が多いでしょう。
この「片方の三角定規を固定して、もう片方の三角定規を垂直にスライドする」のは本質的です。
とても大事なことですが、中学・高校でもあまりこのように描くことはありません。
そして、大学でも設計図など図学に関わる学問をする時以外は、図形を描く機会は少なくなります。
「フリーハンドでササッと図形を描いて考える」ことも大事ですが、しっかり描くことも大事です。
・フリーハンドで描いて、特徴をしっかり理解
・定規やコンパスなどを用いて正確に描いて、頭と身体で理解
受験で「正確な図形を描いてもらう」形式が少ないのは、「採点の難しさ」もあるでしょう。
「正確に」とは「どの程度正確であれば、〜点」という基準が難しいです。
一方で、「基準」に関しては、記述式も同様に「設定が難しい」ことだと思います。
小学生・中学生・高校生が皆タブレットで、
これは
タブレットで調べよう・・・
分からないことは、
すぐにタブレットで分かる・・・
このような学習が一般的になった今こそ、「手で描く」ことは推奨して良いと思います。
「正確な図形を描くこと」は「フリーハンドではなく正確だからこそ分かる」ことがあります。
「採点の困難さ」と「定規など道具の扱い方」などから「正確に描く」のは出題されないかもしれません。
一方で、このようなことを「準備しておく」のは、記述問題を課す学校志望の方は大事と思います。
まずは描いてみる姿勢：「自由」なら自分でサッと決定
今回は「正方形を左上に作る」という少し数学的ではない表現にしています。
問題の例の図形と同様に正方形を作ってゆきます。
ここで、問題では「動く点Pは、辺CD上どこでもよく、一つは点Dに到達した時」とあります。
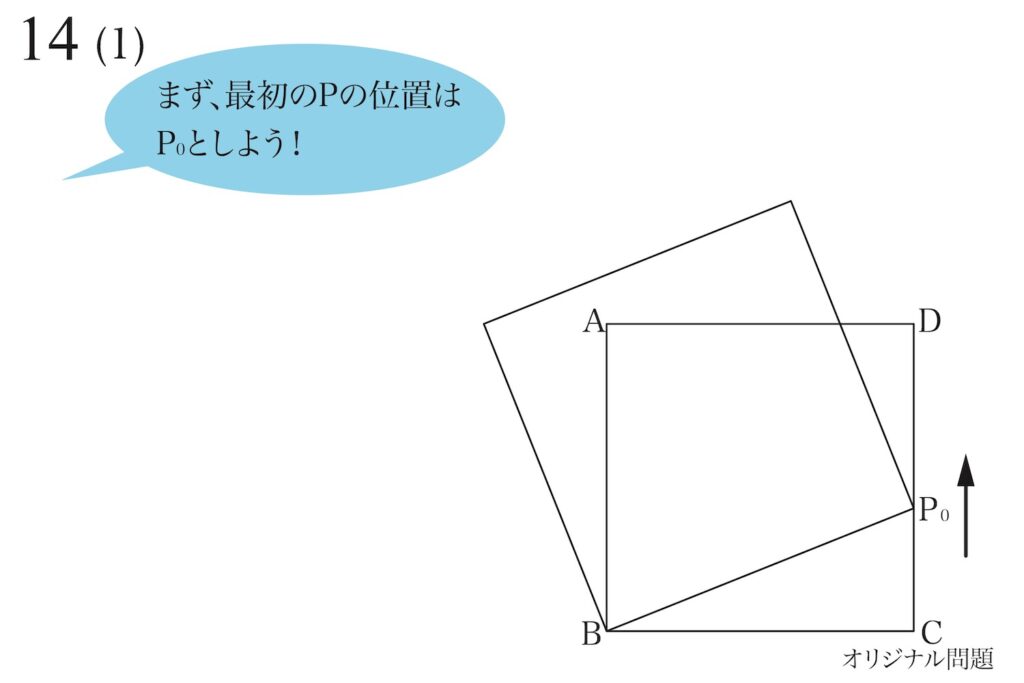
最初のPの位置を「P0」とします。
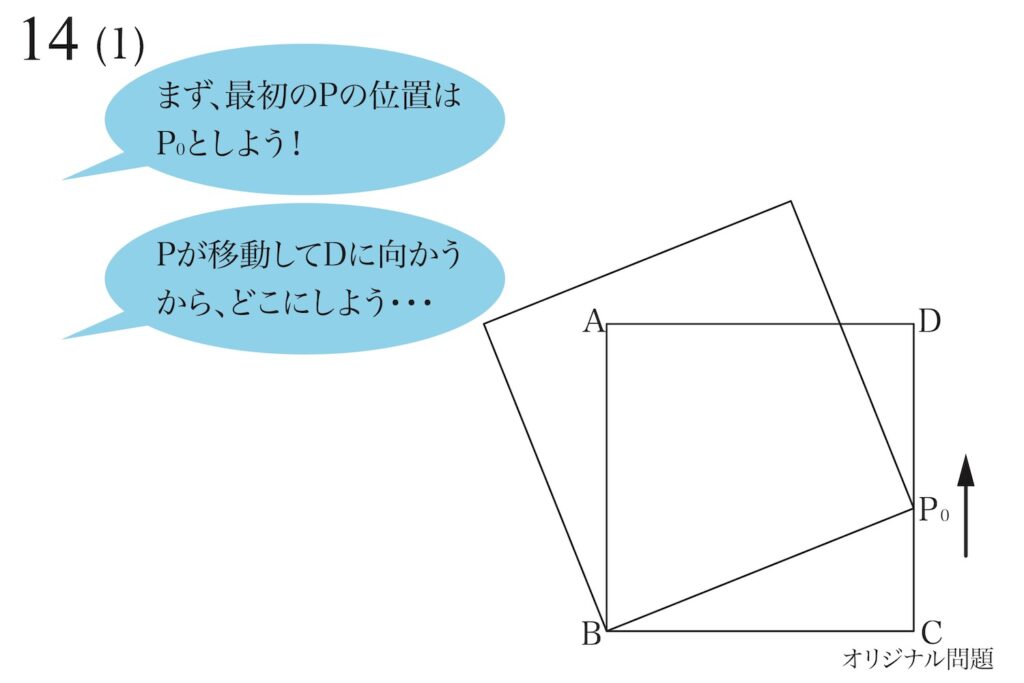
こういう時は、
点Pを
どこにしよう・・・
と悩みすぎないで、
よし！
問題の通りに描いてみよう！
と考えましょう。
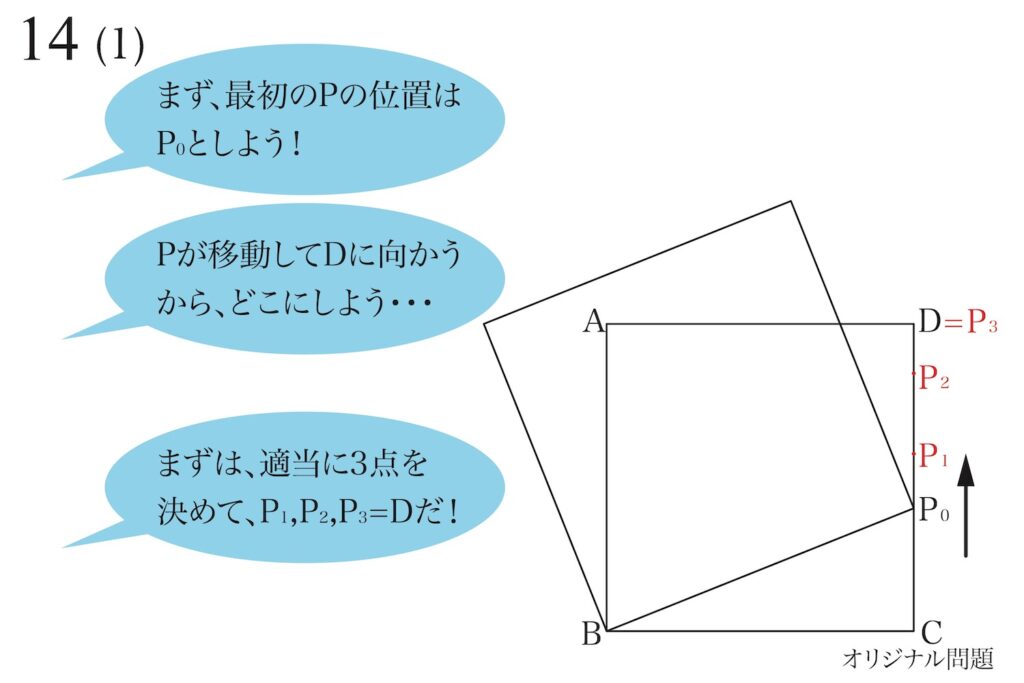
一つは点Dだから、
適当に点Pの位置を決めよう！
と考えて、点P1,P2,P3=Dを決定しましょう。
最初に、
点Pの位置を
どこにしようかな・・・
と悩んだ方は、上の点を参考例に描いてみましょう。
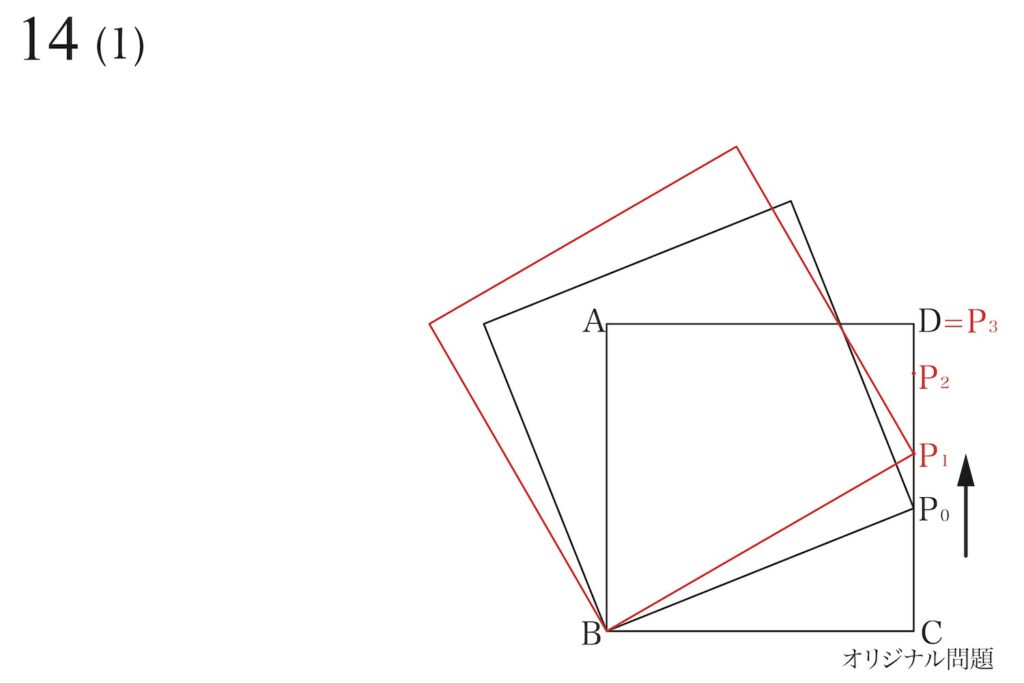
早速、一つ目の「辺BP1を一辺とする正方形」を描きます。
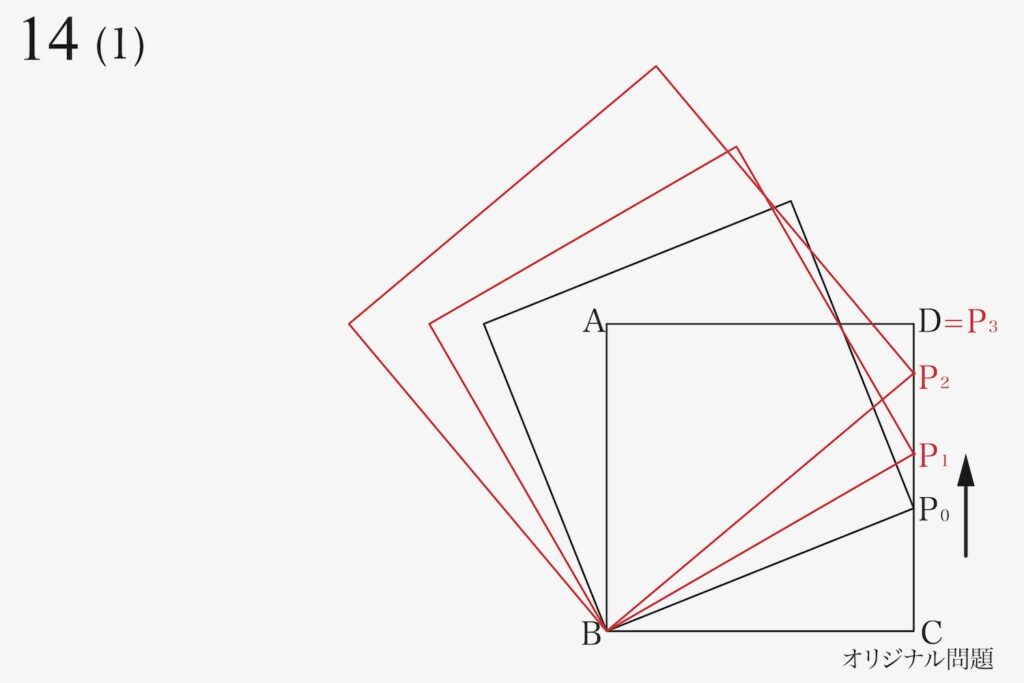
続いて、二つ目の「辺BP2を一辺とする正方形」を描きます。
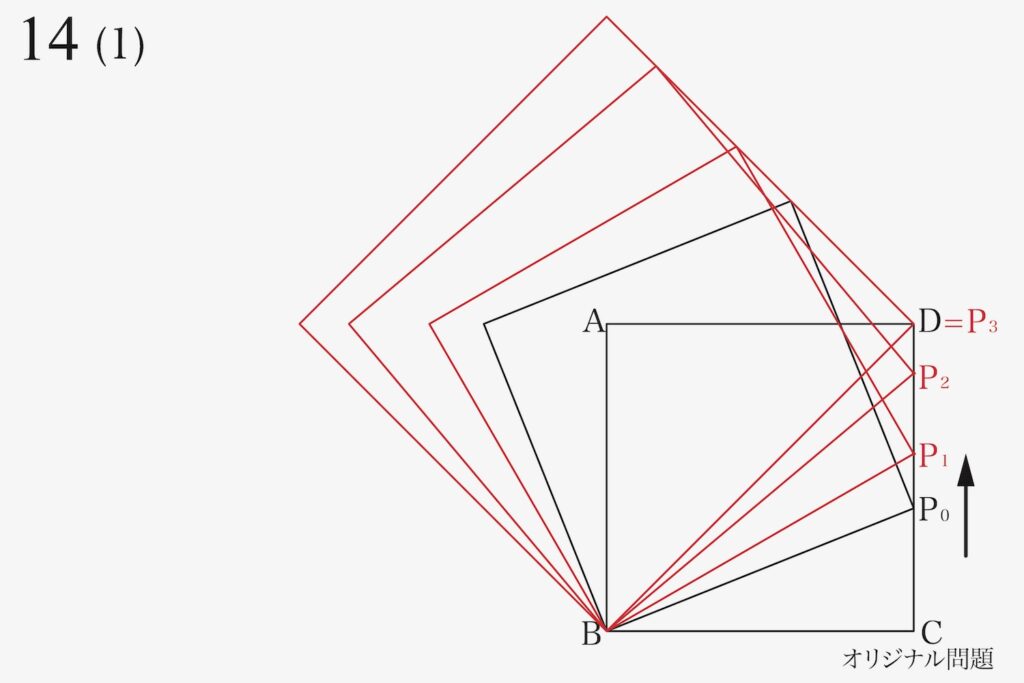
最後に、三つ目の「辺BP3（BD）を一辺とする正方形」を描きます。
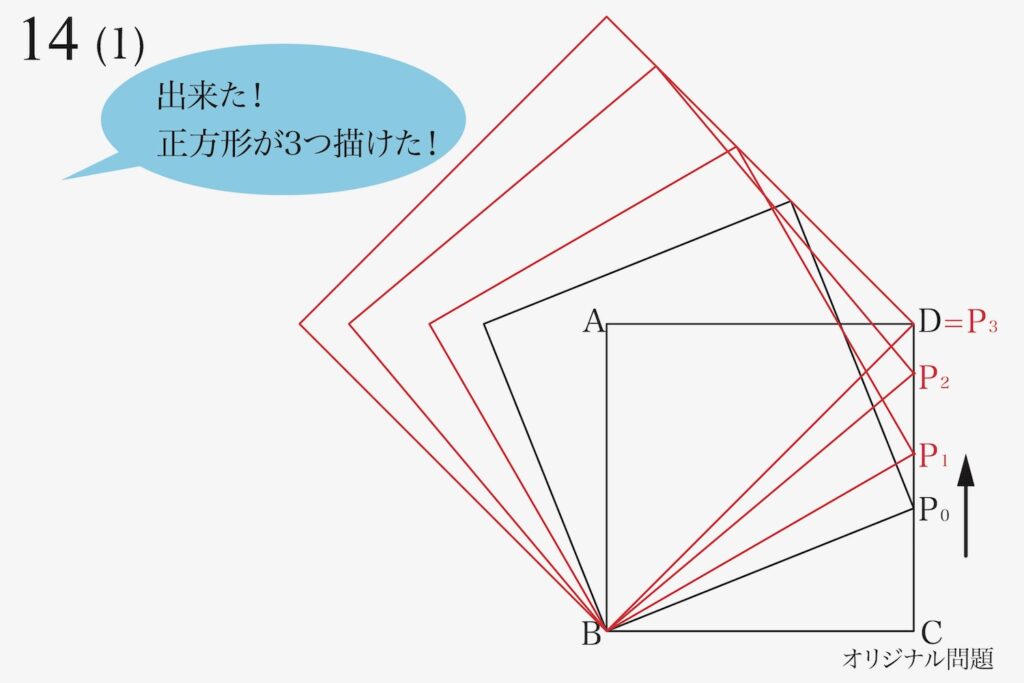
これで、(1)が出来ました。
この図形を見て、
なんか
面白い！
綺麗な感じで、
不思議！
と感じたら、「そういう気持ち」を大事にしましょう。
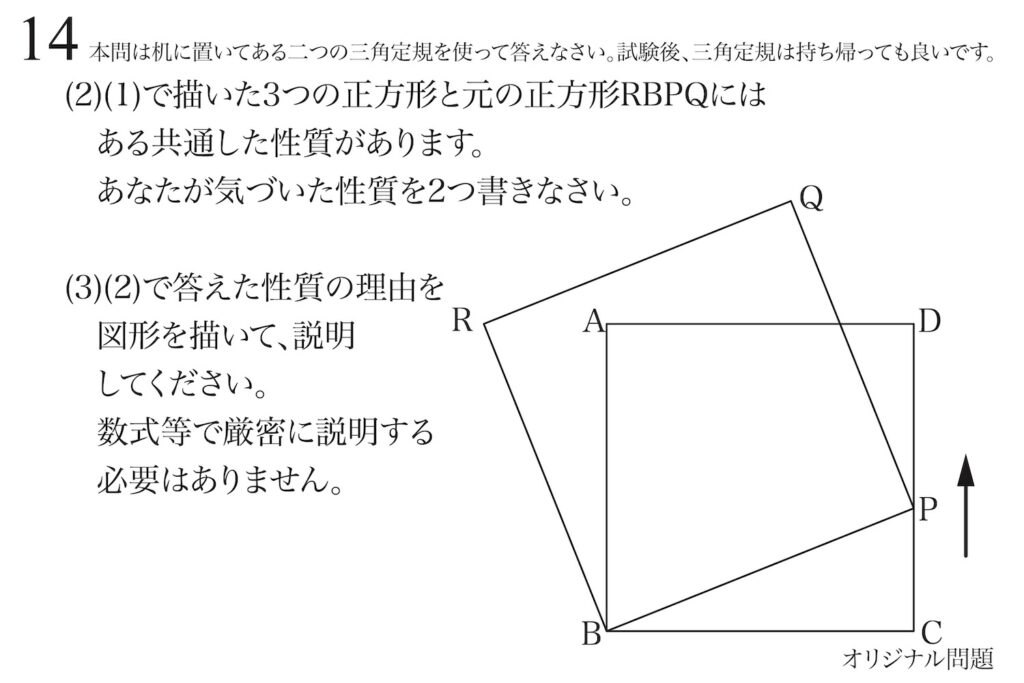
(2)以降は、この図形が「大体正確に描けること」が前提となります。
パッと特徴的な点が分かる方もいらっしゃるでしょう。
共通した性質って
何だろう？
と感じる方は、少し考えてましょう。
上の例以外の「他の三点で正方形を描いてみる」のも良いでしょう。
続きは次回ご紹介します。
