受験期後半から直前期に算数・理科の学力を大きく伸ばす勉強法〜公式を理解して導ける学力・本質的な東大数学の過去問・相似形の面積比の根本的理解・公式と円の面積〜｜中学受験・算数・理科

前回は「補助線を発見する考え方・コツ・ポイント〜図形の線を消してみる発想・「出っぱった図形を整理」する発想・整理する発想と解き方・変わったポイントと「解く鍵」〜」の話でした。

公式を理解して導ける学力：本質的な東大数学の過去問

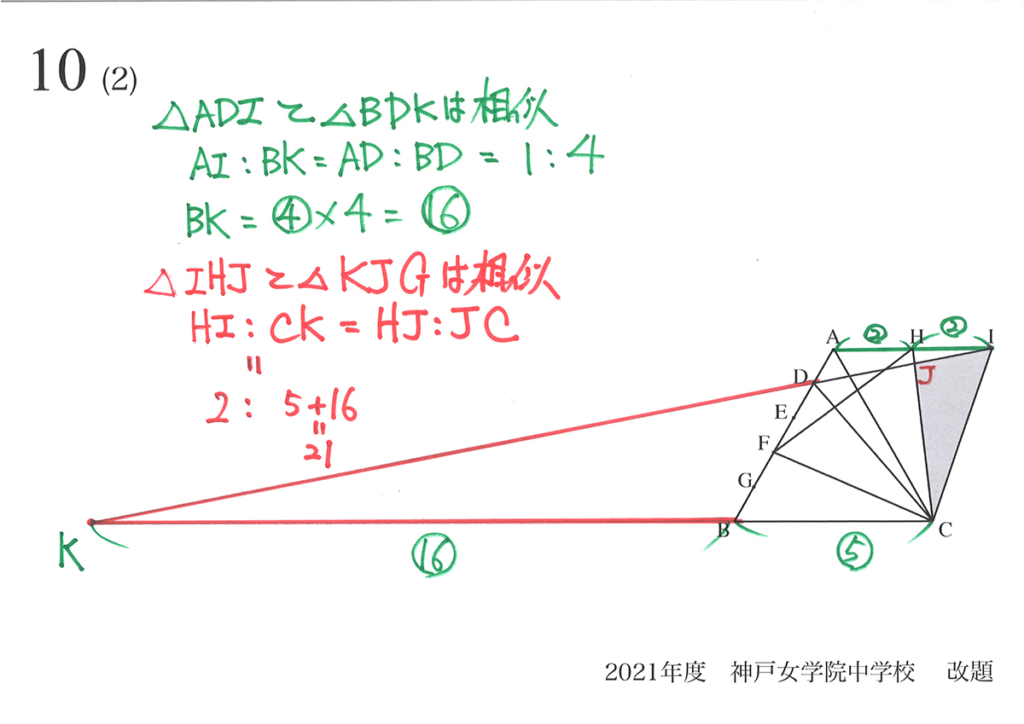
今回は、受験期後半から直前期における算数・理科の効果的な勉強法の話です。

多岐にわたる分野を勉強してきて、図形問題なら様々な補助線を引くことを学んできた受験生たち。

これまで勉強して学力を上げてきた受験期後半から直前期だからこそ、やってほしい事があります。

大学受験の話になりますが、過去に東大数学で下記のような問題が出題された事があります。

実際の問題文とは少し異なりますが、概要は上のような問題でした。

小学生の方は、三角関数sin,cosに関しては気にしないで下さい。

これは「教科書に書いてあり、東大受験生なら常識」の三角関数の加法定理を証明する問題です。

こう考える方も多いかもしれませんが、「この問題を解けた方は少数派」だったと聞きます。

つまり、「教科書の公式を導く」という基本的かつ本質的な問題です。

ところが、東大受験生で「解けなかった方が多い」のが現実でした。

「大学受験の数学」と「中学受験の算数」は全然違いますが、基本的な思想は似ている面があります。

実は「公式をしっかり理解して導ける学力」は非常に大事です。

「公式をしっかり理解する」ことは、解放テクニックやパターンを複数身につけるより良いことです。

ぜひ、様々な公式を復習して「自分で導ける」くらいになってみましょう。

入試で出題されるかどうかは不明ですが、「出題されても出来る」準備はしておくのが良いでしょう。

難関校〜最難関校で「出題される可能性がある」と考えます。

相似形の面積比の根本的理解

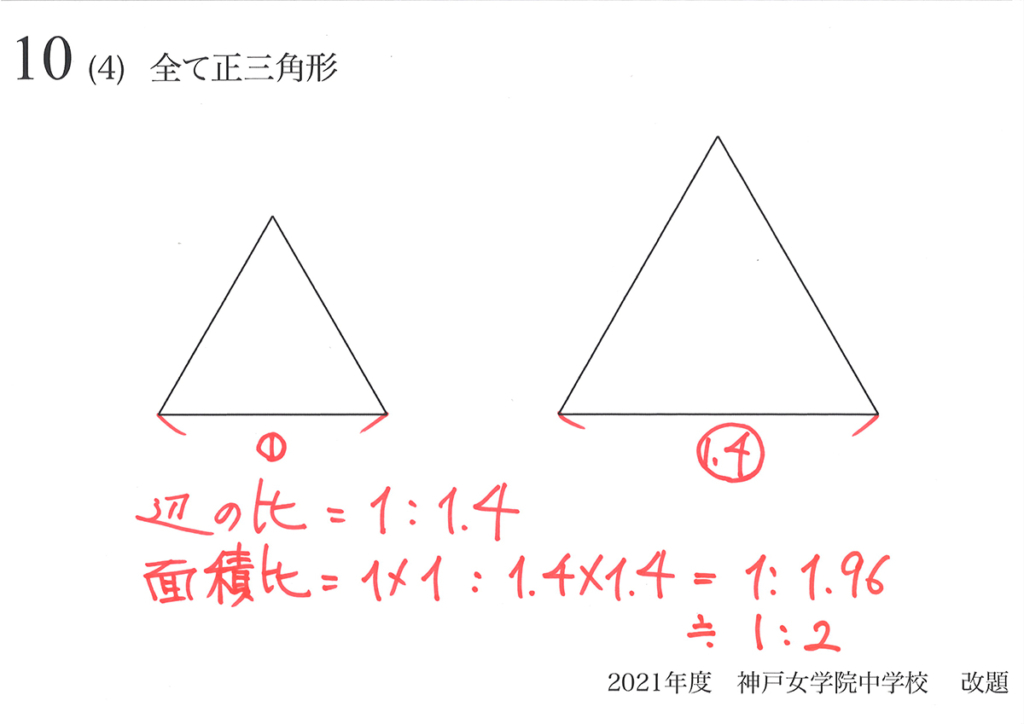
図形問題では様々な辺の比から面積を考えます。

この時「相似形の面積比=辺の比x辺の比（辺の比の2乗）」は、受験生なら知っているはずです。

上のように、辺の比が「1:1.4の相似三角形」なら面積比は「約1:2」なります。

それでは、この面積比の公式が導けるか考えてみましょう。

高校受験〜大学受験では、

このように「何かの事実」を、計算等によって論証して証明する問題がよくあります。

中学受験では「証明」ではなく、「説明」で良いので考えてみましょう。

この「面積比」は、方眼紙に図形を描いて「図形を相似比に応じて拡大すると当然」とも言えます。

「当然」なのですが、算数・数学では「当然です」では証明・説明にならないです。

そこで、しっかり図や式にして、考えてみましょう。

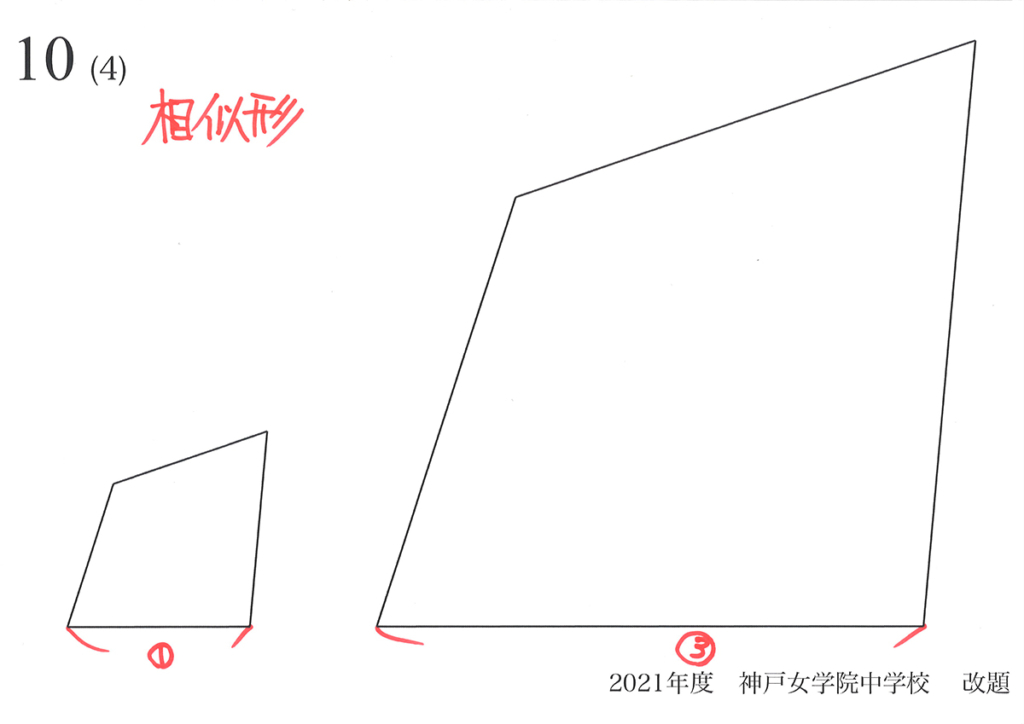
三角形の場合は簡単ですが、歪な四角形の場合は説明できるか考えてみましょう。

この問題は、受験期後半以降は出来てほしいですが、少し考えてみましょう。

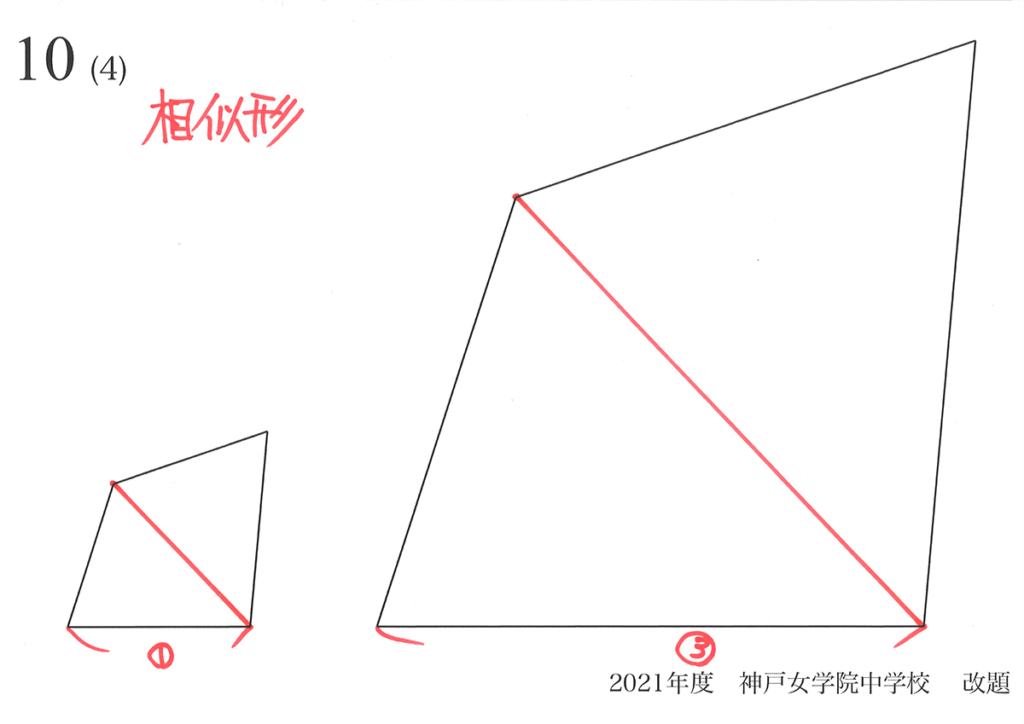
四角形や五角形などは、「分割して三角形にする」のが一つの考え方です。

「困難は分割すると易しくなる」傾向があります。

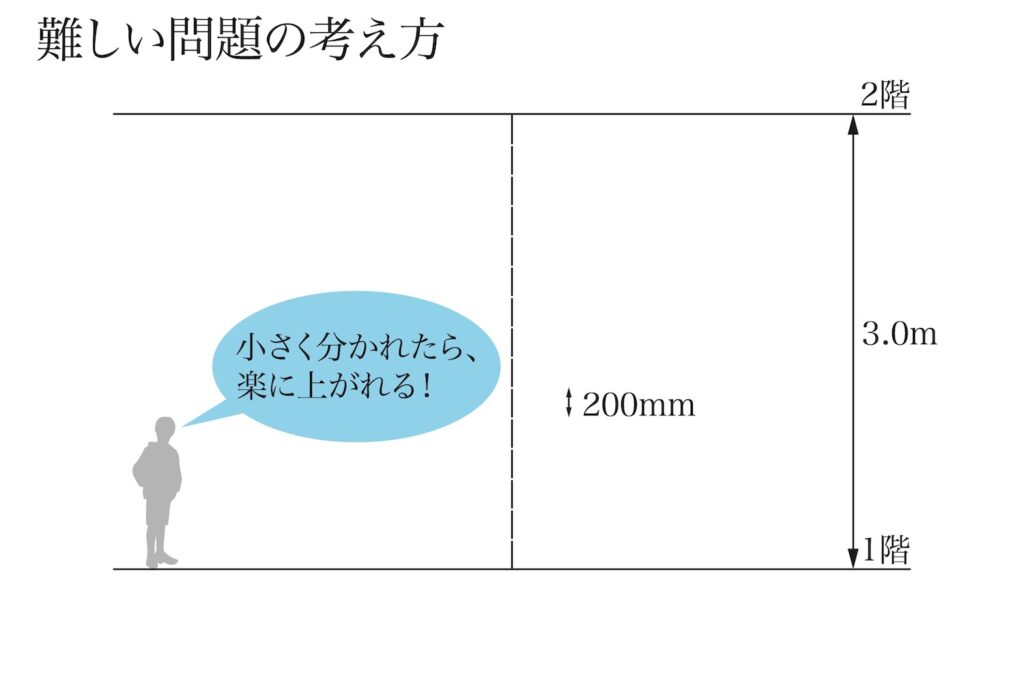
一気に3mはジャンプ出来ませんが、「高さを分割して階段」にすると、

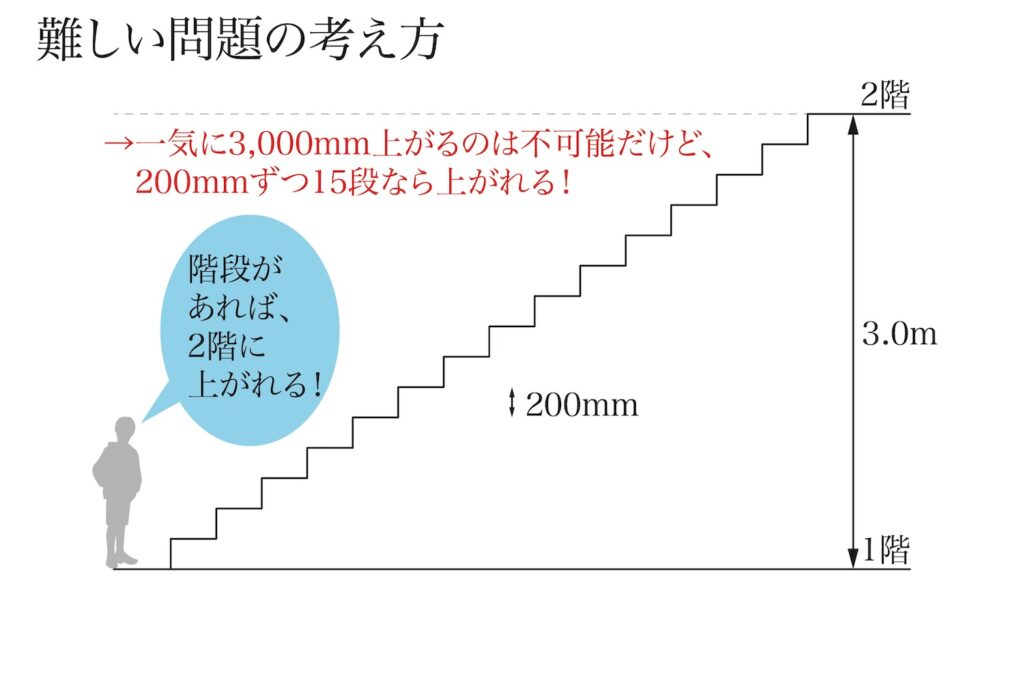
階段によって、上がることが出来るようになります。

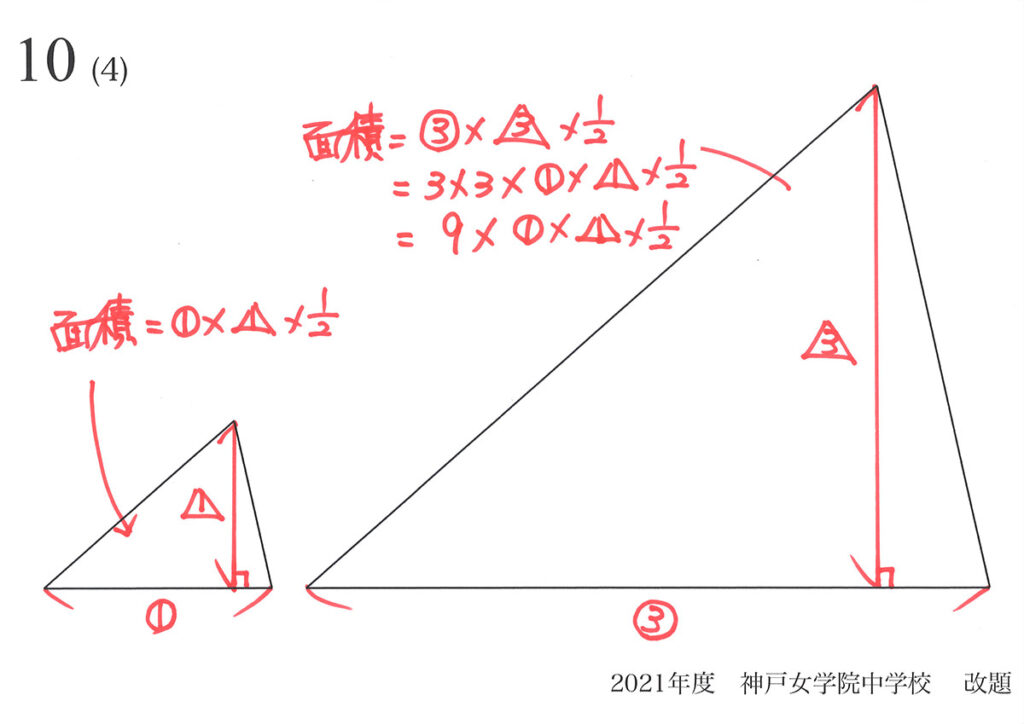
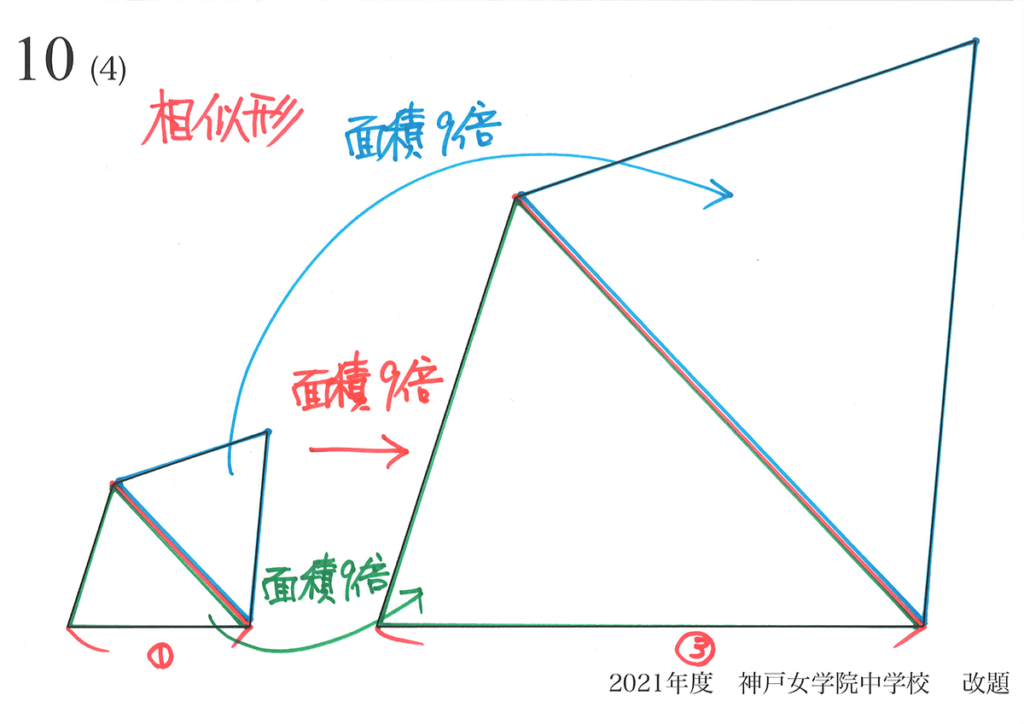
各三角形で「相似形の面積比=辺の比x辺の比（辺の比の2乗）」なので、四角形でも同じです。

ここでは簡単に説明しましたが、詳しくは上記リンクでご紹介しています。

この「相似比の公式の説明」を考えると、図形問題の本質が理解できます。

そして、その過程において、「困難（難しい図形）を分割する（簡単な図形に）」があります。

この「困難を分割」は、算数・数学の難問を解く姿勢として非常に大事です。

このように、「出題されるかどうか」は別として「公式が導けるように理解」することは大事です。

「公式を導く」問題が中学受験で出題されたら、話題を呼ぶでしょう。

「どこまで」はそれぞれなので、「少しでもやってみよう」と考えましょう。

受験期後半から直前期に算数・理科の学力を大きく伸ばす勉強法：公式と円の面積

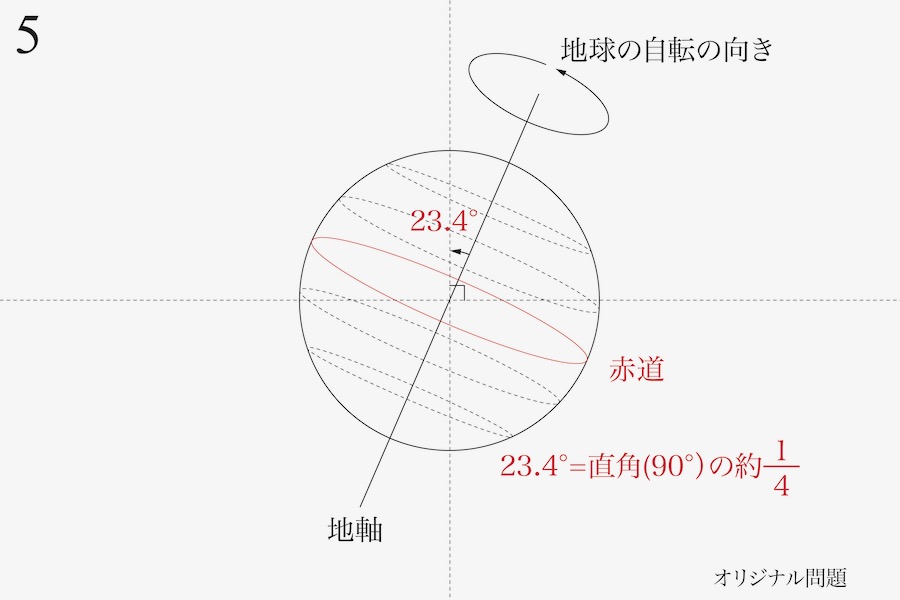
理科の問題で、「南中高度の計算」がよく出題されます。

それでは、この公式を説明できるでしょうか。

下記のような問題が出題される可能性があります。

この問題の「2の説明」がサラッと解ける方は、意外と少ないのではないでしょうか。

この南中高度の公式は、足し算・引き算の順序を入れ替えて下記でも良いでしょう。

上の「その1」と「その2」のどちらが好きかは、それぞれの方の個性によると思います。

どちらでも「好きな方」をしっかり頭に入れて、考え方を復習しましょう。

上の公式の導き方は、参考書・テキスト等に記載されているでしょう。

「絶対分かる」方以外は、ぜひ「南中高度の公式の導き方」を復習しましょう。

「公式をしっかり理解」出来れば、様々な応用問題が解けるようになるでしょう。

天体の問題は結構難しく、点差が開きやすいです。

ぜひ、「公式をしっかり・根本的に理解」して、様々な応用問題も解けるようになりましょう。

公式を復習したら「それで終わり」にしないことが大事です。

すぐに参考書・テキストを閉じて、白い紙に「自分で公式を説明できるか」やってみましょう。

特に直前期においては、「分かったつもり」だけなく「自分で出来るか確認」する姿勢が大事です。

もう一つ、公式に関する問題を考えてみましょう。

天体などでは円・球が登場しますが、中学受験の図形では円に関する問題は少ないです。

それは、「円の重要な性質」は中学・高校数学でたくさん学ぶからです。

円周率は中学以降は「Π（パイ）」と表記しますが、ここでは「α」とします。

円の面積の計算方法は小学校でも習うことですが、すぐに説明できるでしょうか。

ぜひ、白い紙に自分で図を描いて考えて、説明してみましょう。

そして、教科書・テキストに記載されている「円の面積の計算方法」を復習しましょう。

このように「公式の根本的理解」は、算数・理科の学力を大きくアップさせるでしょう。

中学受験では様々な「新たな試み」がなされていて、記述問題の増加が考えられます。

このような「公式を説明する」問題は、根本的で「学問への姿勢」として最適です。

「公式の説明」は出題される可能性があり、これを理解すると応用問題が解けるようになります。

「算数・理科の公式を総復習する」ことは、とても良い総まとめになります。

そして、これまで学んだ様々なことの理解が深まり、大きく成績がアップするでしょう。

次回は下記リンクです。