前回は「天体を苦手にならない勉強法〜地球から太陽と月の距離・大きな数の計算と単位・天体が得意になるコツ・地球・太陽・月・星などを描く〜」の話でした。
地球から太陽・月の距離の問題
地球から1.5億km離れたところにある太陽と、地球から38万km離れたところにある月は、地球から見るとほぼ同じ大きさに見えます。
太陽の大きさは直径140万km、光は1秒間あたり30万kmの速さで移動するとして以下の問いに答えなさい。途中経過の式なども書きなさい。
(1)太陽から出た光が地球にたどり着くまでに、何秒間かかりますか。
(2)この文章にある「地球から見ると太陽と月がほぼ同じ大きさに見える」ことを図で描いて下さい。地球、月、太陽を描き、長さや大きさの正確さは問いません。
(3)この文章から月の直径を計算し、最も近いものを下記から選びなさい。
ア 2500km
イ 3500km
ウ 4500km
描きながら考える姿勢：手や思考が止まらないようにする
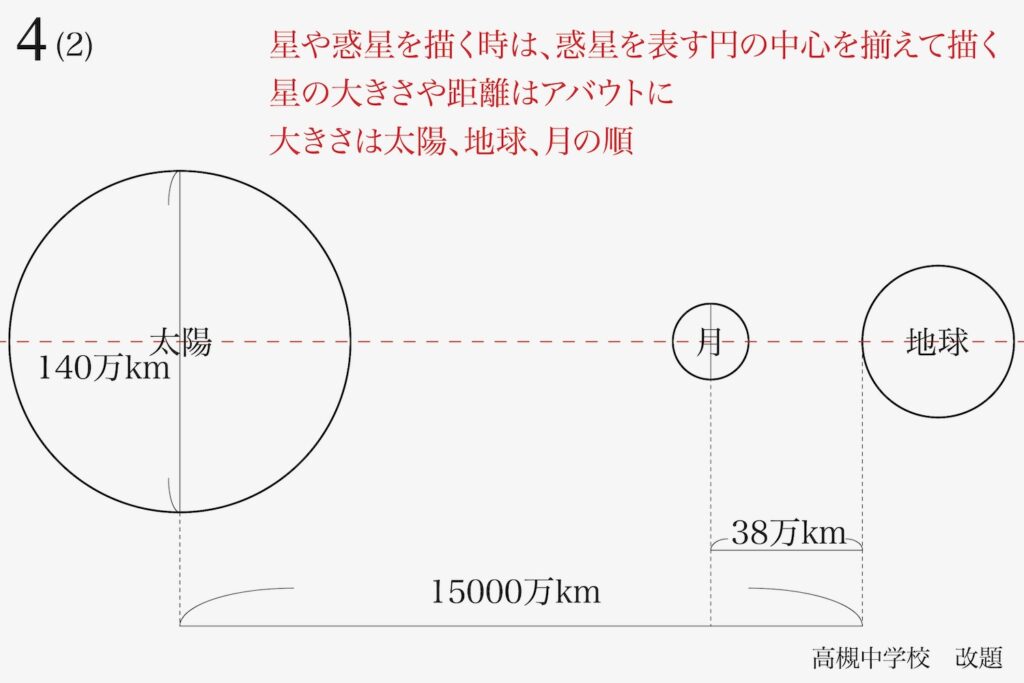
この問題は基本的ですが、こういう問題は必ず図・簡単な絵を描きましょう。
ある程度、問題などに慣れてくると、
あっ、
これは「あれ」だな！
とドンドン手が動くことがあります。
小問などで「間違いなく思った通り」であれば、そのように解くのが時間がかからないので良いでしょう。
一方で、大問でいくつかの小問に分かれている場合は、距離や角度等を間違える可能性があります。
そして、前の問題のミスが後の問題の解答に影響を与える可能性もあります。
それを防ぐためにも、図や絵を描いて確認しながら進みましょう。
・惑星を表す円の中心を一直線上に揃える
・大きさや距離は「大体で良い」感じで、大きさは太陽>地球>月の順
問題が基本的に記述が多いタイプであれば、「前の問題のミスの影響」は採点の際に、
ああ、ここで
間違えたから、こっちもミスったな・・・
ここは考慮して、全てX（バツ）にはしないで、
5点の減点にしておこうか・・・
と考えることがあるでしょう。
・「図や絵を描く」ことを大事に
・上手くなくて良いので、丁寧に描く
・図形問題の場合、「図形全体と補助線」を描く
確かに図を描いた方が
いいけど、時間がもったいない・・・
テストでは、1分1秒が
大事だから・・・
「答えのみ」のタイプが多い試験の場合も含め、時間を惜しまずに「描いて考える」のが良いでしょう。
「描く時間がもったいない」気持ちは、とても分かります。
・描きながら、問題のポイントを考える姿勢
・図や絵を描くことで「手や思考が止まってしまう」のを防ぐ
描いている間も自然と考えていますが、「考えること」を強く意識してみましょう。
すると、問題のポイント等が見えてきて、「手が止まってしまう」のを防ぐでしょう。
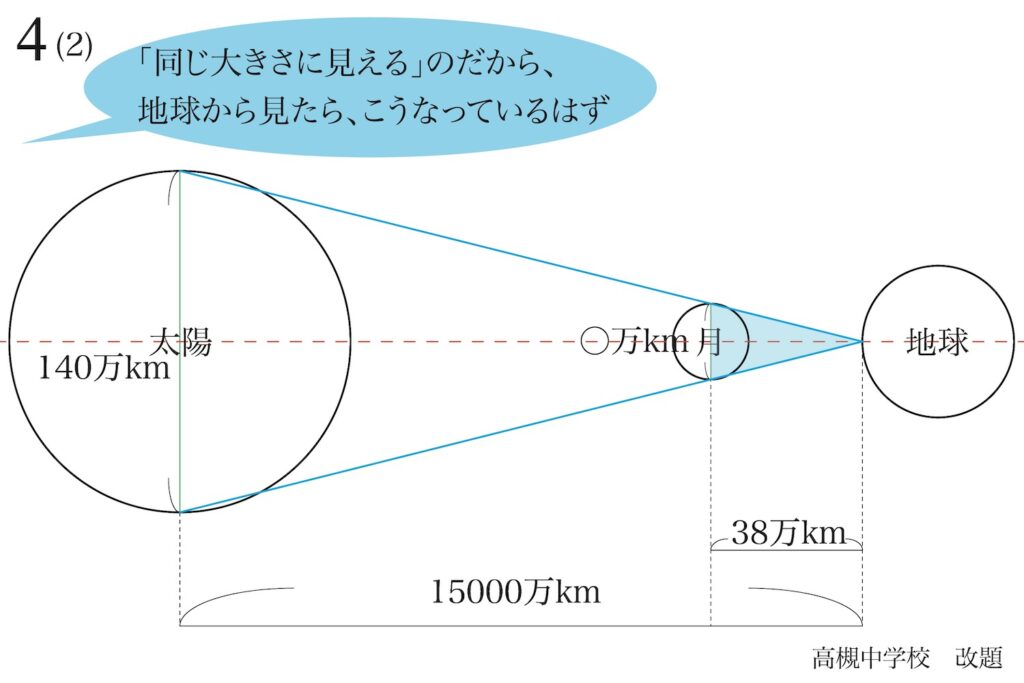
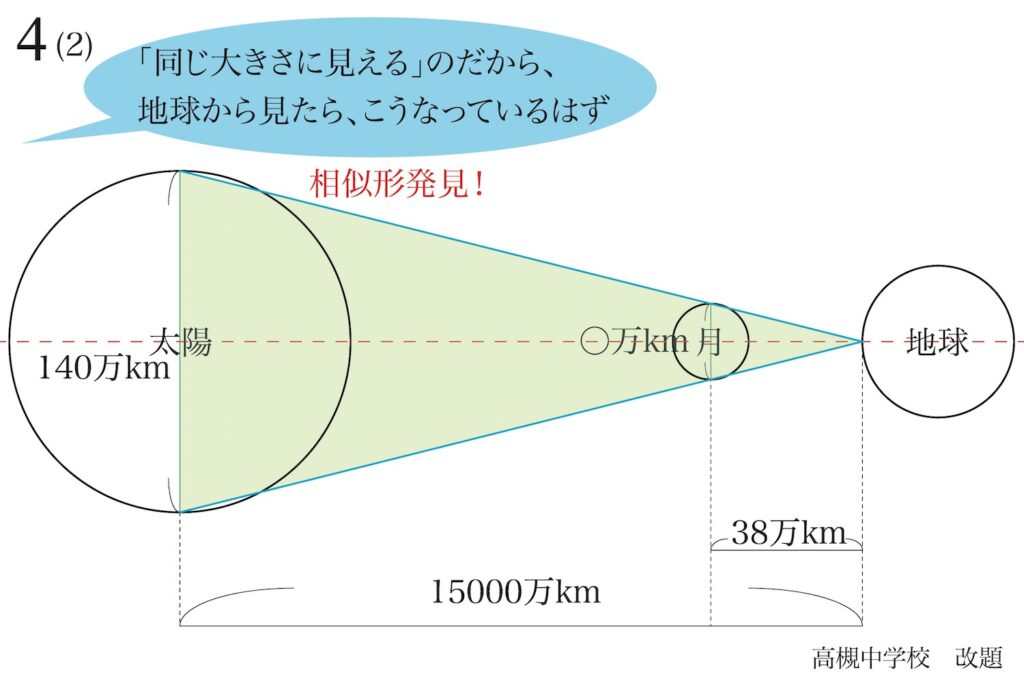
前回、太陽・月・地球の位置関係と相似形を見出したので、(3)の月の直径を求めます。
算数の図形問題と異なり、理科の天体などの相似形は「描けばすぐに分かる」ことが多いです。
基本的な相似形なので、相対する辺の比を考えます。
この比を書かずに、一気に辺の比から計算しても良いでしょう。
あとはこの計算をするだけですが、「15000」というかなり大きい数字が分母にあるのが気になります。
分母の大きな数の「000」を約分するためには、分母に「000」がないか考えましょう。
もう少しで計算できそうです。
計算結果が出て、答えは（イ）と分かりました。
これは出来たし、
計算にもそんなに時間かからなかったよ！
これがオーソドックスな解き方ですが、計算するところを少し工夫することを考えましょう。
今回は、選択肢があるので「どれか分かれば良い」です。
そこで、「アバウトに計算する」ことを考えてみましょう。
アバウトに計算する姿勢：スケールが巨大な天体
途中の「割り算しやすくするために、万を0000に表記」するまで同じです。
ここから掛け算と割り算になりますが、「約分できると楽」です。
「分母の15=3×5」で、割り算は「大きな数で割ると簡単になる」ので「5で割れる近い数40」にします。
5で割れれば、サッと計算できます。
だいぶ簡単になりました。
こうなったら、
すぐに計算できるよ！
ここから、真面目に計算しても良いですが、もう少し「楽をする」ことを考えましょう。
分子に「14」がありますが、これが「3の倍数だったら、とても楽」です。
14に近い3の倍数は12か15なので、どちらか選びましょう。
ここで、先ほど「38を少し大きくして40」にしました。
そこで、こっちでは「少し小さめ」の12を選びましょう。
「大きくして、さらに大きくする」と計算がドンドンずれます。
そこで、「大小混ぜて、良い塩梅で」計算しましょう。
これで、筆算せずに「大体の計算」が出来そうです。
約分できて、一気に計算できます。
これで、計算結果は「3200kmより少し大きい」数字になるはずなので（イ）が答えです。
なるほど！
これなら、時間が短くて済むね！
40と38の違いは少しだけど、
14と12は10%以上違うから・・・
最後の3200を10%上げて
3520にすると、似た答えになるね！
これは一例ですが、このように「計算は大雑把に、簡単に」するようにするのも一つの手です。
・大体の、大まかな数字が大事
・計算するときは、数字を多少増減させて、アバウトに計算
特に、天体の問題は「大雑把な数字」が大事です。
てこ・てんびん、食塩水などスケールが身近な場合は、このような計算はしない方が良いでしょう。
対して、天体はスケールが大きい、というよりも「スケールが巨大」です。
0が沢山出てくる天体の問題では、「出来るだけ簡単に、大体の数字を掴む」ようにしましょう。
・分子を、分母の約数の中で「比較的大きな（出来れば最大の）約数」を持つ数字にする
・「少し大きく」と「少し小さく」を織り交ぜて、計算結果の違いを最小限に
これは「簡易な計算の一例」で、
これを考えるなら、
僕は真面目に計算した方がいいかな・・・
という方は、筆算して計算しましょう。
計算するのは慣れたけど、
時間かかるし・・・
計算ミスするよりは、
こっちの方がいいかも・・・
という方は、一つの参考にしてください。
「答えのみ」や「大体の数字」を求める場合は、上のアバウトに計算することを考えると良いでしょう。
天体の問題を解く際には、こうした「アバウトな感じ」を考えてみるのも良いと思います。
