前回は「受験生の失速しない・スランプにならない姿勢〜公式と解く力・公式を考えて理解する〜」の話でした。
超直前期の心掛け
新年明けましておめでとう御座います。
2023年となり、いよいよ関西圏の中学受験は残すところ「あと2週間ほど」となりました。
関東圏の中学受験も残り2週間ほどの学校もあり、多くは一月を切りました。
大学受験は共通テストが間近になり、受験生は精神的に緊張する時期です。
今回は、超直前期の最も大事な姿勢に関する話です。
具体的な考え方等は、中学受験を対象としますが、高校受験〜大学受験でも同様と考えます。
男子小学生僕、
大丈夫かな？
男子小学生私、
合格できるかしら？
模試などの成績が群を抜いている方以外は、誰しもこういう考えが頭がよぎります。
でも、「大丈夫か？」「合格できるか？」を考えるよりも、「体調をしっかり」しましょう。
今まで「自分のやってきたこと」に自信を持って、着実に勉強して突き進みましょう。
合格する力を高める姿勢：模試を復習
模試などで「出来なかった問題」は復習しましょう。
算数（数学）、理科（物理・化学）などでは、「出来なかった問題」をしっかり習得することが大事です。
模試の判定・合格率も気になりますが、模試の最も大事な点は下記です。
・当日の試験と同様の内容・似た問題でトレーニング
・自分の出来ない箇所・分野を意識して、出来るようにする
「当日のトレーニング」は誰しも理解していることですが、どうしても「判定」ばかり気になります。
「トレーニング」と同様に大事なことは、「出来なかった部分・分野を明確に意識」することです。
男子小学生僕は、過去問を
何度もやったよ！
女子小学生過去問を3回くらいやったから、
大体覚えちゃったよ！
「過去問」は大事なので、この姿勢は大いに良いですが、模試も大事です。
塾講師今年のA中学の模試は
このような問題を出そう・・・
模試は、塾などのプロが何十年もの過去問を分析して、新しい問題を作成しています。
特に、算数（数学）は模試の「出来なかった問題」を、もう一度復習しましょう。
算数と理科の公式をしっかり理解
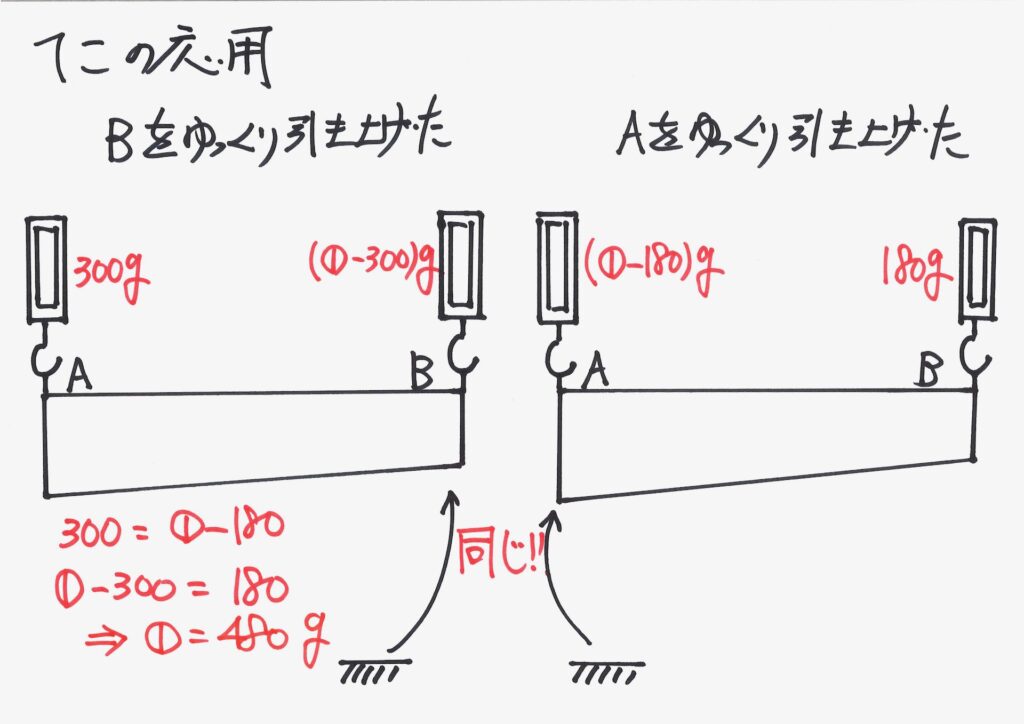
算数や理科は「公式丸暗記ではなく、公式の内容を理解」することをお勧めします。
「面積比の公式」を理解する話を、上記リンクでご紹介しています。
「辺の比と面積比」は公式というよりも基本原理に近いので、こういう基本事項は全て押さえましょう。
それは、ニュートン算・旅人算・てんびん算などの「基本的考え方」も同様です。
中堅校志望の方で基本事項が「あやふやな」方は、公式暗記より、「基本をしっかり」しましょう。
理科の電気の問題で、「合成抵抗」という考え方があります。
合成抵抗に関する話を、上記リンクでご紹介しています。
この「合成抵抗」は、抵抗（電球）がたくさんある時などに、「素早く解ける」考え方・公式です。
このような問題を「答えのみ・素早く解く」ことが求められる学校を志望している方は、
男子小学生色々な合成抵抗は
考えられるようになったよ！
女子小学生合成抵抗を
考えた方が早いね！
これらの公式は、しっかり覚えておいた方が良いでしょう。
複雑な回路に対して、
出題者Aの電球の明るさは『一つの電池・電球』の時の
何倍ですか？
このように「明るさ」を問う問題があります。
こういう問題に対しては、「合成抵抗」を求めれば、すぐに出来ます。
「公式を暗記」する意義・効果が非常に大きいので、「暗記した方が良い」です。
一方で、大問形式が多く、「思考力を求める問題」が出題される学校を志望する方は、
出題者なぜ、Bの電球より
Cの電球の方が明るいか、答えてください。
「公式より理解」を優先しましょう。
電気の問題で、「対話形式」や「実験しながら考える問題」などがあります。
こういう問題において、「合成抵抗」の考え方は「無意味」ではありませんが、あまり役に立ちません。
電気の問題は「主役は電圧」です。
「電圧があるから、電流が流れる」のであり「電流があるから、電圧が発生」するのではないのです。
実は「電流があるから、電圧が発生」することが物理現象であり、非常に大事な現象です。
男子小学生えっ、
そうなの？
女子小学生それは
知らなかった・・・
この事実は「小学生の理科」の範囲を超えるので、中高で学ぶのを楽しみにしてください。
こういう事実を「説明しながら問題を解いてもらう」形式の出題はあり得ます。
とにかく、基本は「電圧」です。
「この場合の合成抵抗は〜」と、ひたすら暗記を固めるよりも、「基本を固める」ようにしましょう。
現在の「超直前期」は、無理に暗記を固めるよりも「暗記をおさらいする」姿勢が良いでしょう。
そして「総合的な理解力」を深めて、しっかり学力を上げてゆきましょう。
次回は上記リンクです。
