前回は「おすすめ暗記方法：暗記カード・プリント〜あと10分早起き〜」の話でした。
公式と解く力
受験直前期は、受験生の方は皆気持ちが焦ります。
そのなか、算数（数学）や理科の公式を総まとめしている方も多いと思います。
ここの公式を
もう少し！
受験する学校の出題傾向によりますが、「公式を丸暗記する」のは「ある程度」にしましょう。
なんで？
公式を覚えないと、
出来ない問題もあるでしょ。
「公式を知らないと出来ない」問題もあります。
一方で公式の考え方をしっかり理解して、解けるようになることに重点を置いた方が良いでしょう。
算数でも理科でも、様々な公式があります。
たくさん
覚えたよ。
例えば「相似形の面積比=(辺の比)x(辺の比)」という事実がありますが、これも「公式」かもしれません。
これは公式というよりも「原理」に近いですが、こういう「原理に近い」公式はしっかり理解して、覚えましょう。
さらに、「なぜ？そうなるのか？」を理解していると、解く力が上がるでしょう。
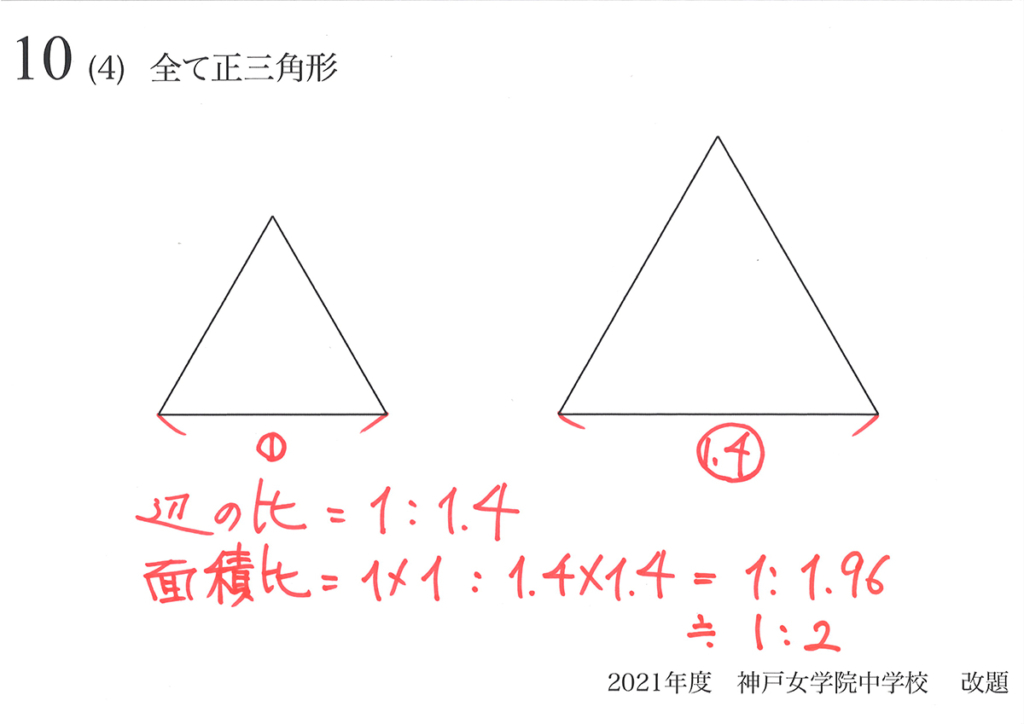
「相似形の面積比=(辺の比)x(辺の比)」は、しっかりと「面積とは何か？」を計算すればわかります。
もう
覚えているよ。
こういう原理・事実は、覚えておいた方が良いでしょう。
公式を考えて理解する
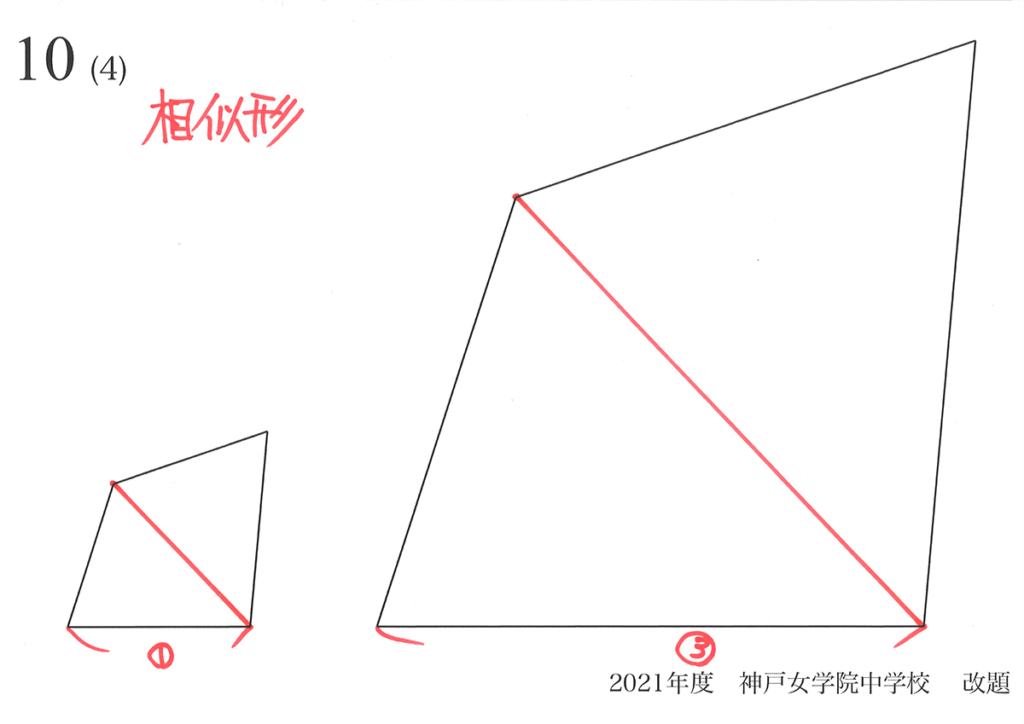
三角形で成立する「相似形の面積比=(辺の比)x(辺の比)」は、四角形でも成立します。
これを考えるには、様々な考え方がありますが、一つの考え方は「分割する」です。
難しい問題でも図形でも「小さく分ける」と分かりやすくなる事が多いのです。
公式を復習したり、覚え直すときに、「なぜだっけ？」と少し考えて「考え方」も復習しましょう。
そうすることで、理解が深まり、「考え方・解き方の引き出し」が大きくなります。
「公式をただ丸暗記」しても、「公式を使うだけで解ける問題」というのは意外と少ないのです。
「ただ暗記している人より、理解している志望者に入学して欲しい」と考える出題者は、少し変化球を考えます。
この問題は、公式を使うと
「早く解ける」けど・・・
少し変えて、
変化をつけよう。
「公式そのまま」の問題を出題する傾向が強い学校もあるかもしれません。
難関校〜最難関校の算数・理科で「公式そのまま」という問題は少ないでしょう。
このとき、「公式を使えば、早く解ける」かもしれませんが、「公式を理解している」方に重点を置きましょう。
直前期に焦らない・失速しない・スランプにならない姿勢
あの公式も
覚えなきゃ！
公式をしっかり固めないと、
算数と理科が不安・・・
と感じている受験生の方もいらっしゃるかもしれません。
これまで一生懸命勉強して、学力がだいぶ増強された直前期だからこそ、「弱いところ」が目立ってきます。
そして、弱点を最もよく知っているのは、自分なので、
あの公式が
あやふやだから、不安・・・
当日、公式を
うっかり間違えたらどうしよう・・・
と不安が増えて、焦るのは避けましょう。
まずは、「平穏な気持ち」が最も大事です。
焦るとスランプになったり、失速する可能性が出てきます。
例えば、算数の図形問題で「チェバの定理」や「メネラウスの定理」をご存知の方もいるでしょう。
僕、覚えたよ。
でも、時々、
分母と分子が混乱する時がある・・・
私も時々
間違えそうになるわ。
「すでにしっかり覚えた」方は良いでしょう。
でも、こういう公式を覚えられなくても、不安になったりするのはやめましょう。
実は、僕は「チェバの定理」や「メネラウスの定理」は知っていますが、パッとは出てきません。
えっ、本当？
あまり必要性を感じないのです。
これらの図形の公式は、よく考えると「分母・分子にも意味がある」のです。
この意味では、「チェバの定理」などを覚えている効果はあります。
一方で、図形問題は、補助線によって相似形を作ったりする基本的姿勢が最も大事です。
こういう基本姿勢がしっかりできていれば、どんな難問でもある程度はできるでしょう。
年号などの暗記は、ある程度は「語呂合わせ」など自分の好みのやり方で覚える必要があります。
でも、算数や理科の「考える問題」の公式は、必ずしも覚えなくても良いでしょう。
でも、公式があった方が、
早くできるんじゃない？
確かにそういう問題や場面もありますが、「公式をそのまま当てはめて解ける」問題は少ないでしょう。
たしかに
そう感じる。
こういう公式を「覚えられない」と感じると、失速やスランプの原因になるかもしれません。
「公式を覚えるより、問題が解けることが大事」です。
なんでも「覚えなければ！」と考えるよりも、「一つ一つしっかり解く」姿勢をしっかり固めましょう。
