電気・回路の実戦的考え方 4〜対称性の性質・「折り返したら同じ」部分は「同じ状況」・回路・電線の形状と対称性・電池の役割と電圧・回路にかかる電圧・対称性から分かること・電球や抵抗の位置・数と対称性〜｜中学受験・理科

前回は「電気・回路の実戦的考え方 3〜対称軸と中心・重心・モノの最も重要な性質・地道に計算して考える姿勢・電流から電圧を考える・点から点で下がる電圧・回路全体を考える・部分から全体へ・性質と計算〜」の話でした。

対称性の性質：「折り返したら同じ」部分は「同じ状況」

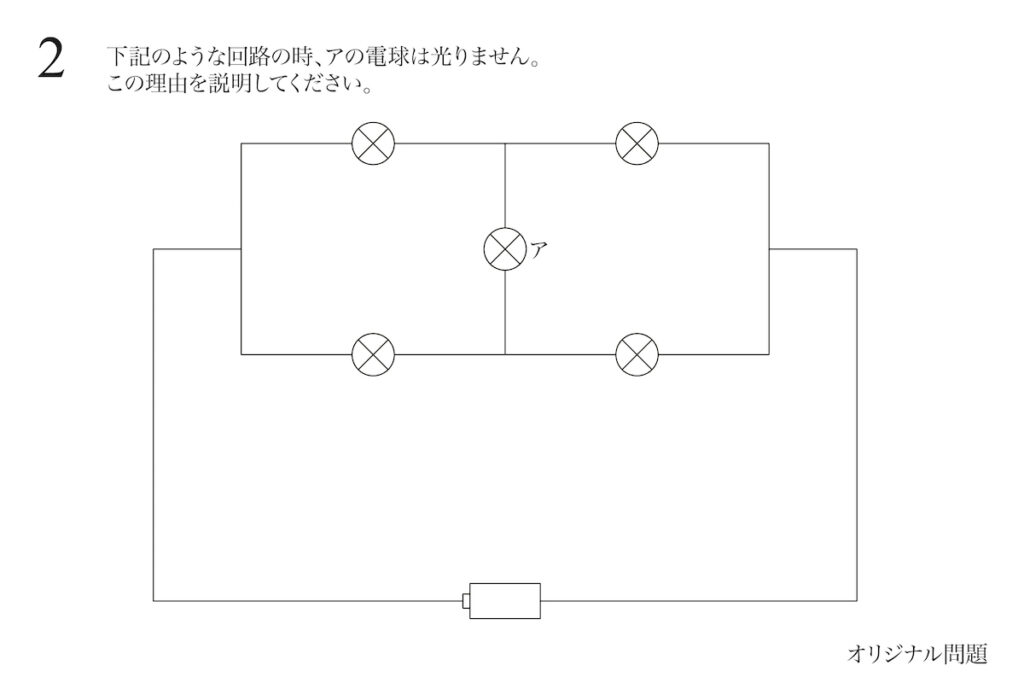
比較的シンプルなタイプの回路のを考える時、対称性に注目して考えました。

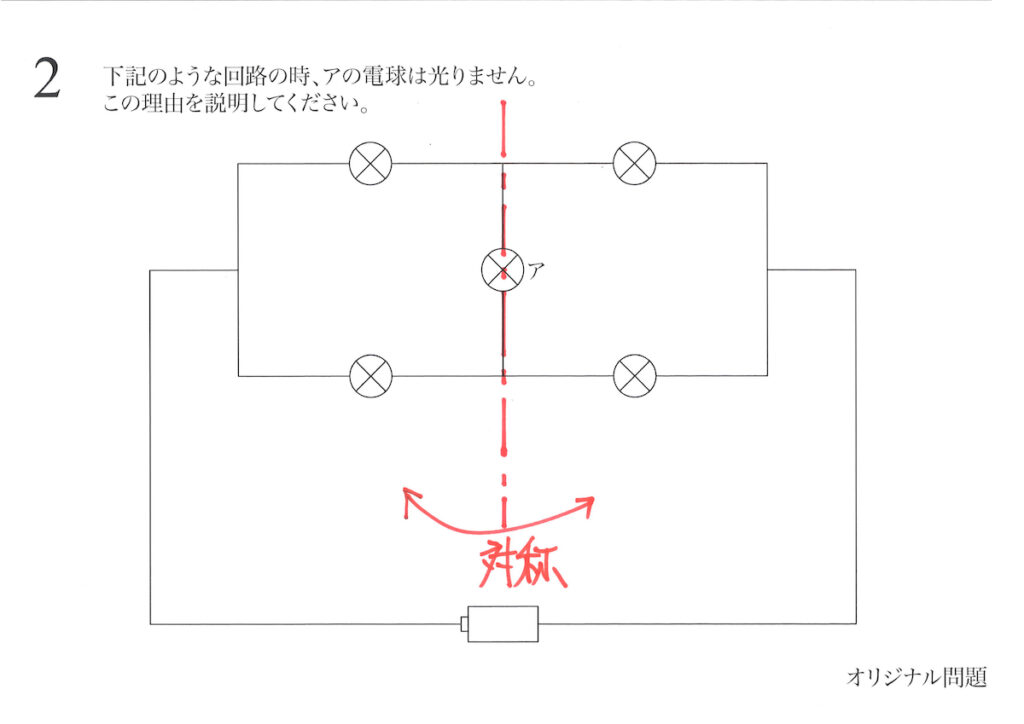
回路の中心線（アの電球を通る直線）に対して、回路は「左右に折り返して同じ」対称性があります。

対称性がある時「折り返したら同じ部分」は「同じ状況」になります。

この「対称性を持つ部分・箇所」が「同じ状況」になることは、本質的な事です。

理科・算数（数学）で、とても大事な対称性の性質は、厳密に考えると難しい面があります。

「直感的に理解」または「大体のイメージで理解」で良いでしょう。

回路・電線の形状と対称性

この「電池・電圧は対称ではない」ことは、とても大事なポイントです。

問題を説明する際、「回路に対称性がある」と説明したのは「電圧は別」という意味です。

それでは、上の回路 1と問題文の回路は同じでしょうか、違うでしょうか。

ちょっと考えてみましょう。

ここでは、「電熱線の長さによる違い」は考えないようにします。

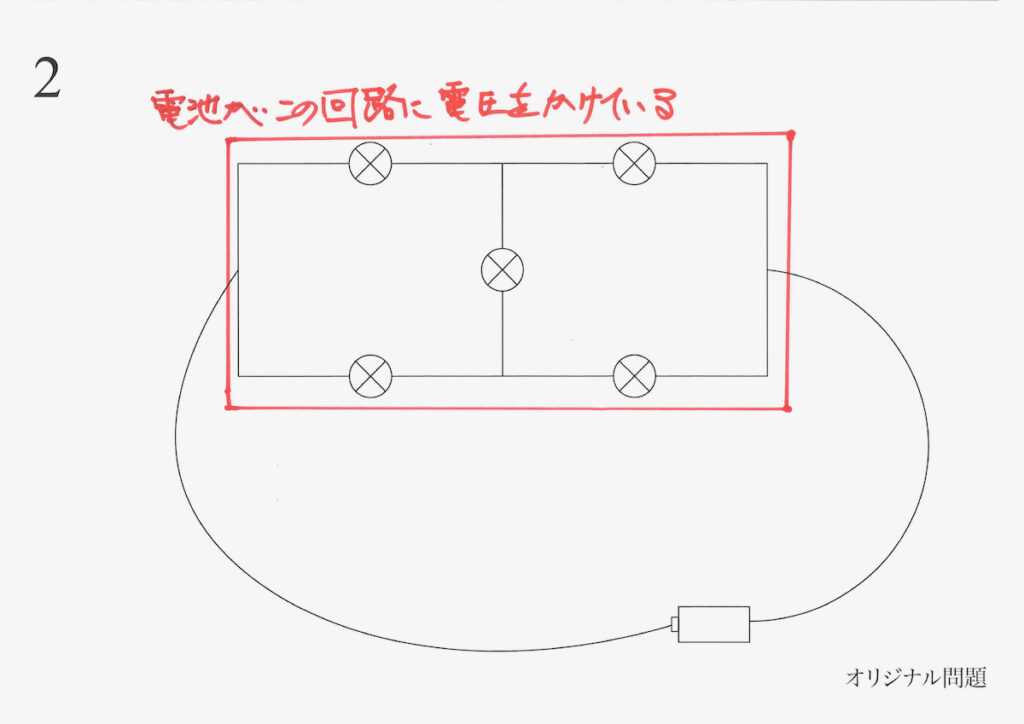
上の赤枠で囲んだ回路に「電池が電圧をかけている」と考えれば、同じです。

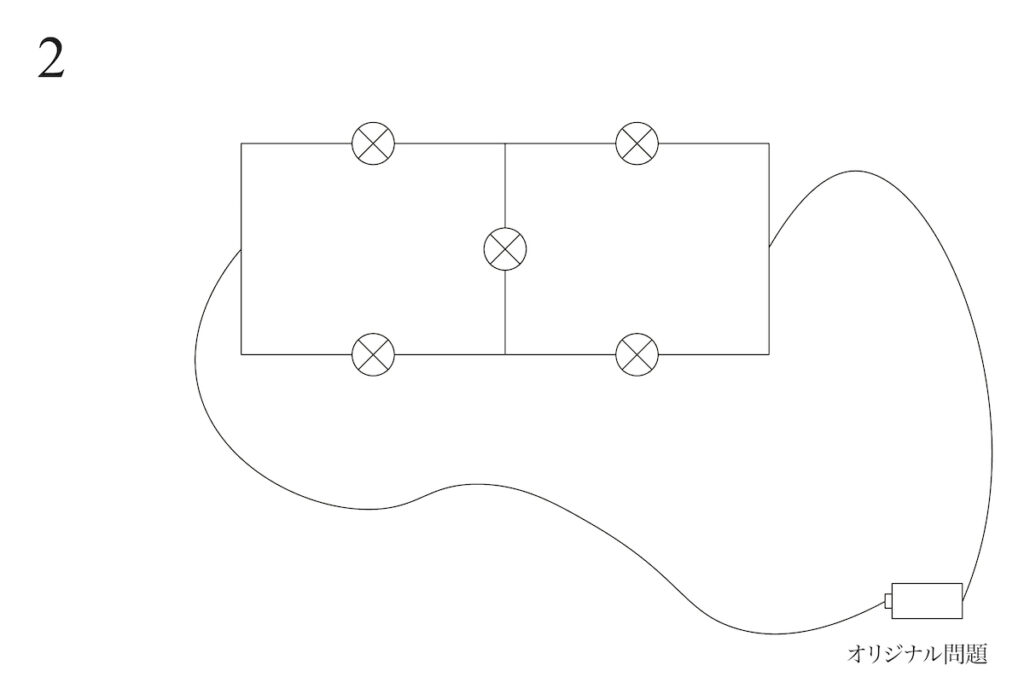
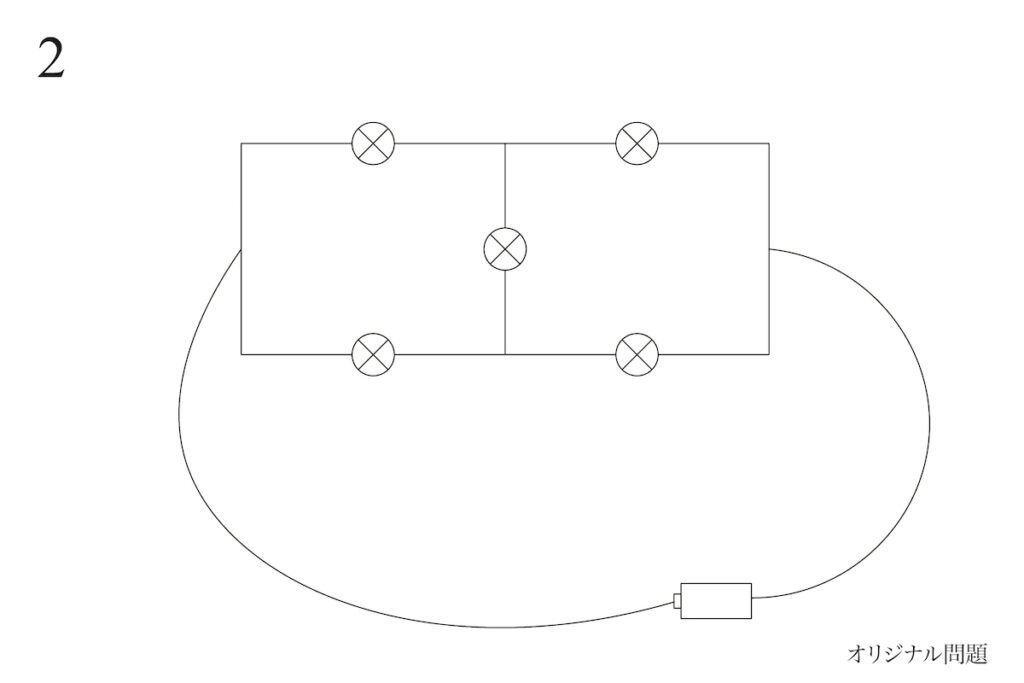
それでは上の図の回路 2と、問題文の回路は同じでしょうか、違うでしょうか。

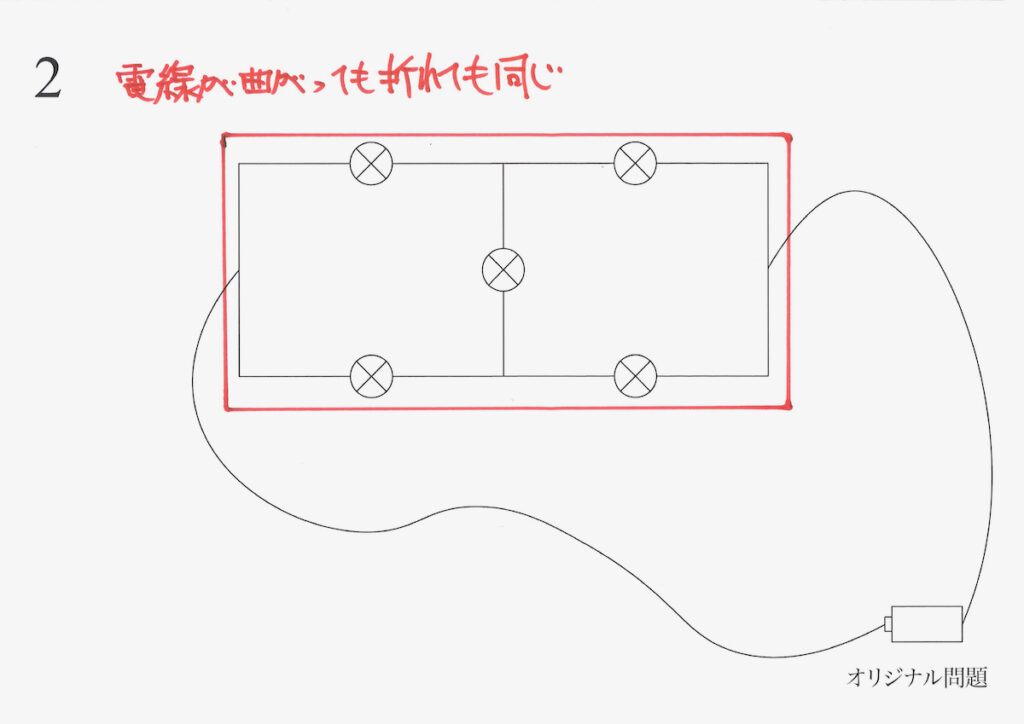
電線が曲がっても折れても、問題文の回路と上の図の回路 1・回路 2は同じです。

もし、「電熱線の長さの影響」を考えると、問題文の回路・回路 1・回路 2は「異なる回路」になります。

回路の問題では、「電線・電熱線の抵抗は無視する」ことが多いです。

それは、「電線・電熱線の抵抗を考える」と問題が複雑になるからです。

「電熱線の長さの影響があり、回路の電熱線の長さが2倍になった時・・・」などの問題もあるでしょう。

特殊な問題以外では「電線・電熱線の抵抗は無視」ですが、問題文をよく読むようにしましょう。

ここでは、「電熱線の長さの影響を考慮しない」とします。

電池の役割と電圧：回路にかかる電圧

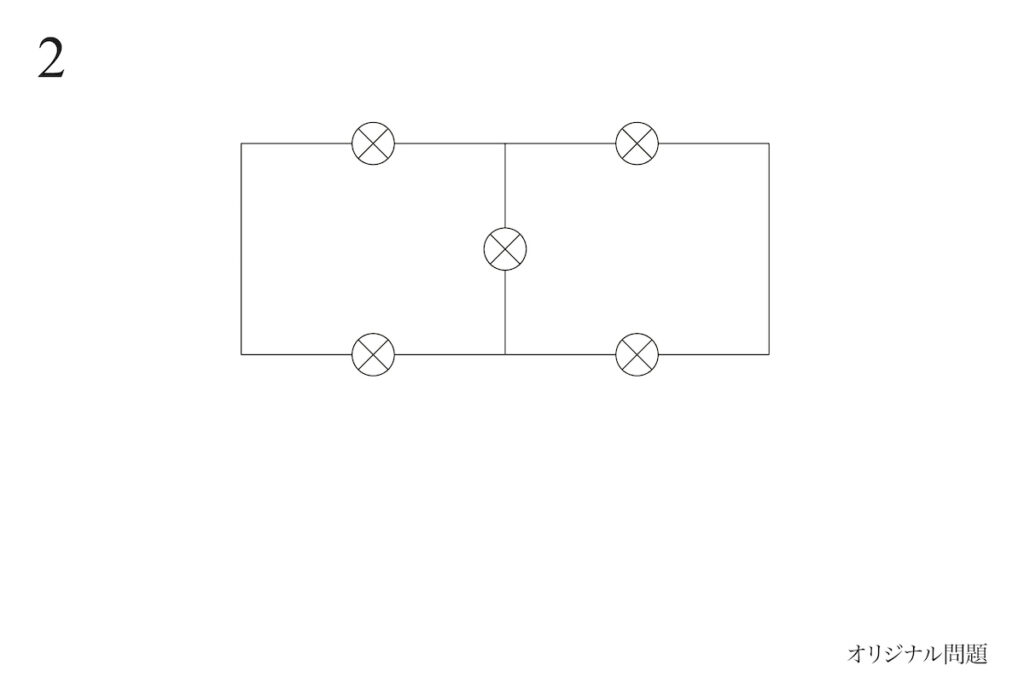
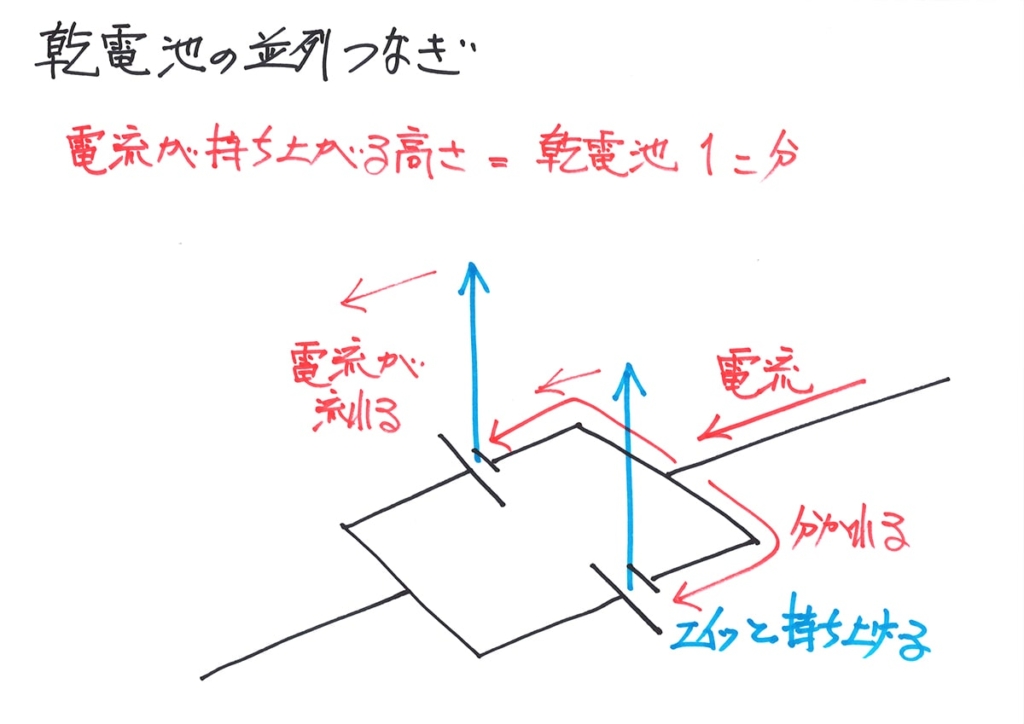
電池は「電圧をかけて、電流をグイッと持ち上げる」役割です。

電池は「回路に電圧をかける」立場です。

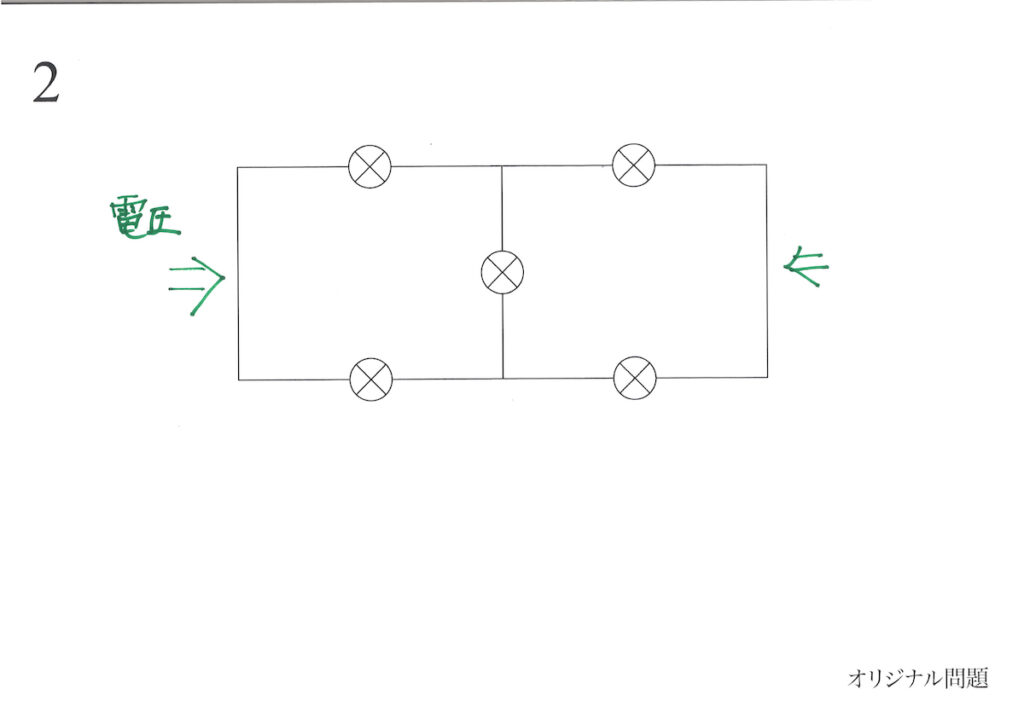
そこで、上の図の「基本回路」を考えてみましょう。

問題文の回路・回路 1・回路 2は、「同じ部分」があります。

この「回路の電球・電線部分」に「両側から電圧がかかっている」ことになります。

電圧とは「電気を押し出す力」や「電気に圧力を加える力」と考えると良いでしょう。

つまり、電池とは「電流を流すポンプのような役割」をしています。

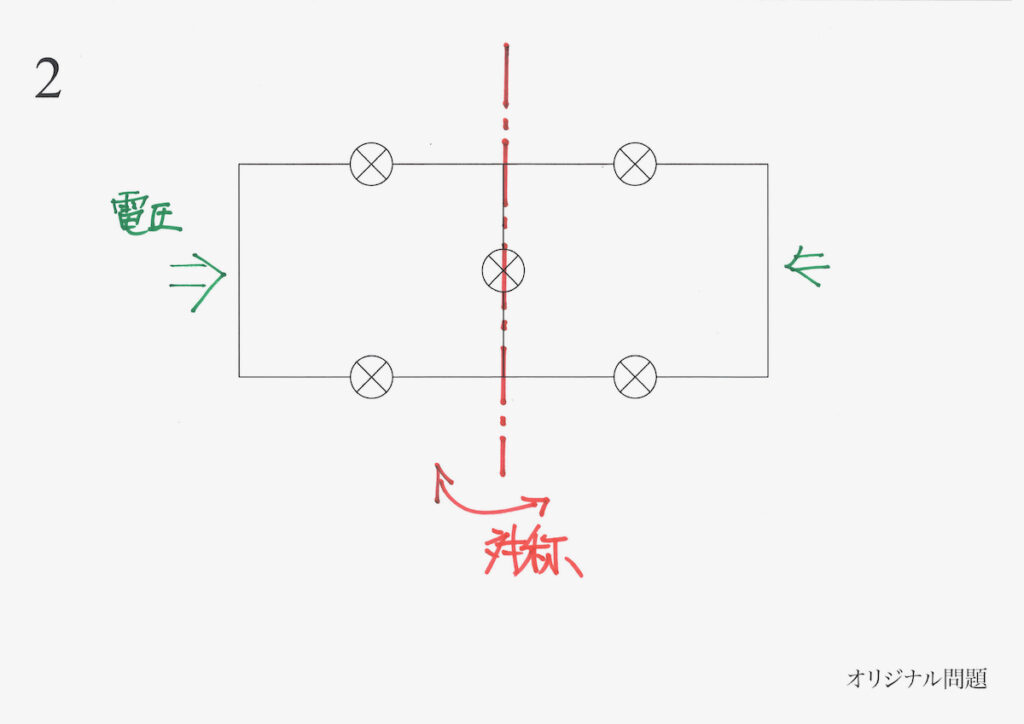
回路だけを考えた時、やはり左右で対称となります。

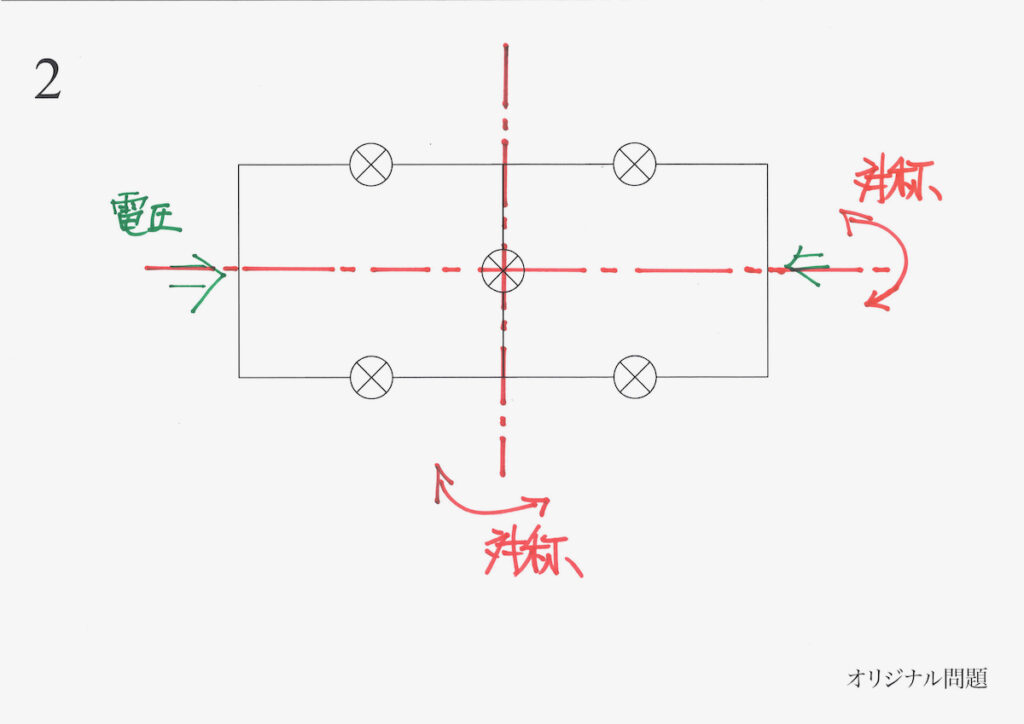
上下の軸と左右の軸の二つの軸で、この回路は対称性があります。

対称性から分かること

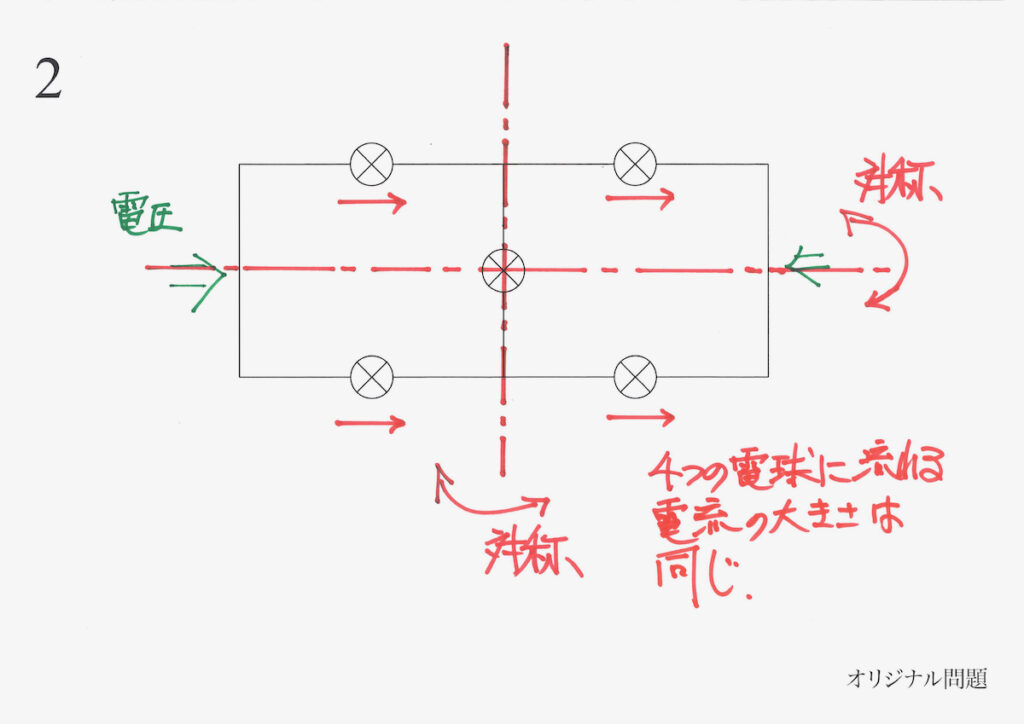
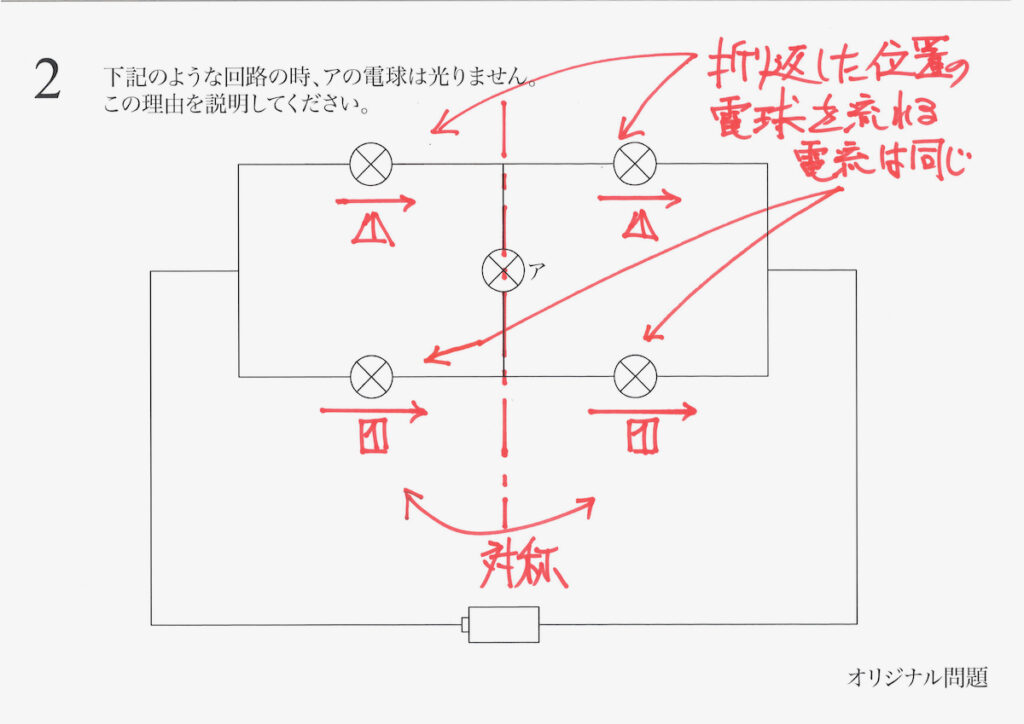
回路に「上下左右で対称性がある」ので、「四つの電球に流れる電流の大きさは同じ」になります。

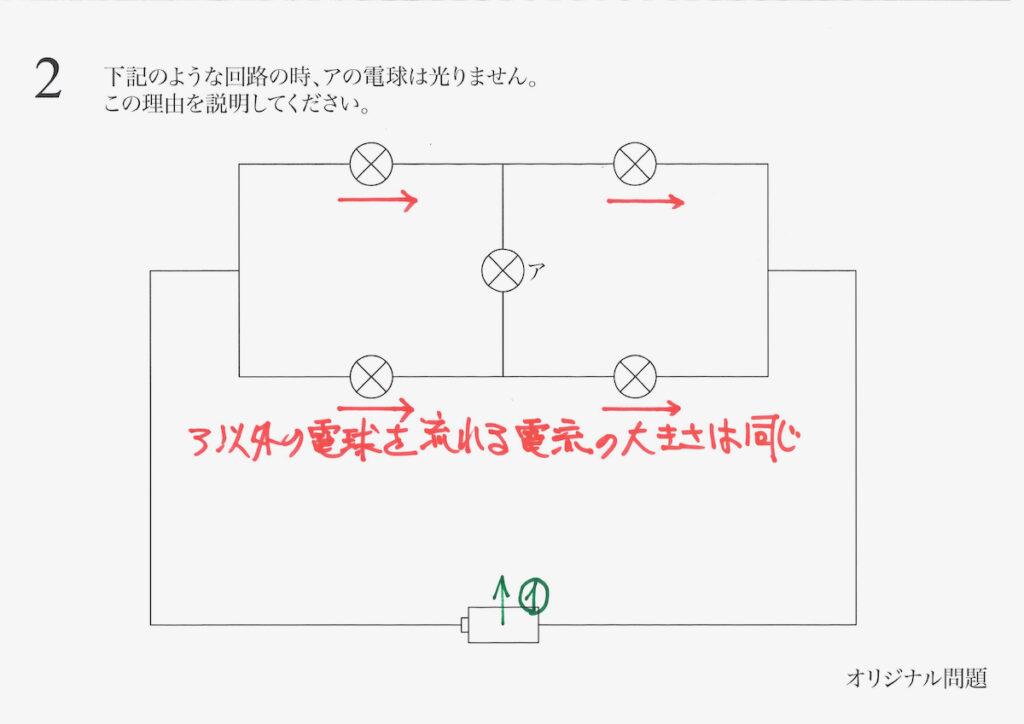
すると、上図のように「ア以外の四つの電流の大きさは同じ」という事実が分かります。

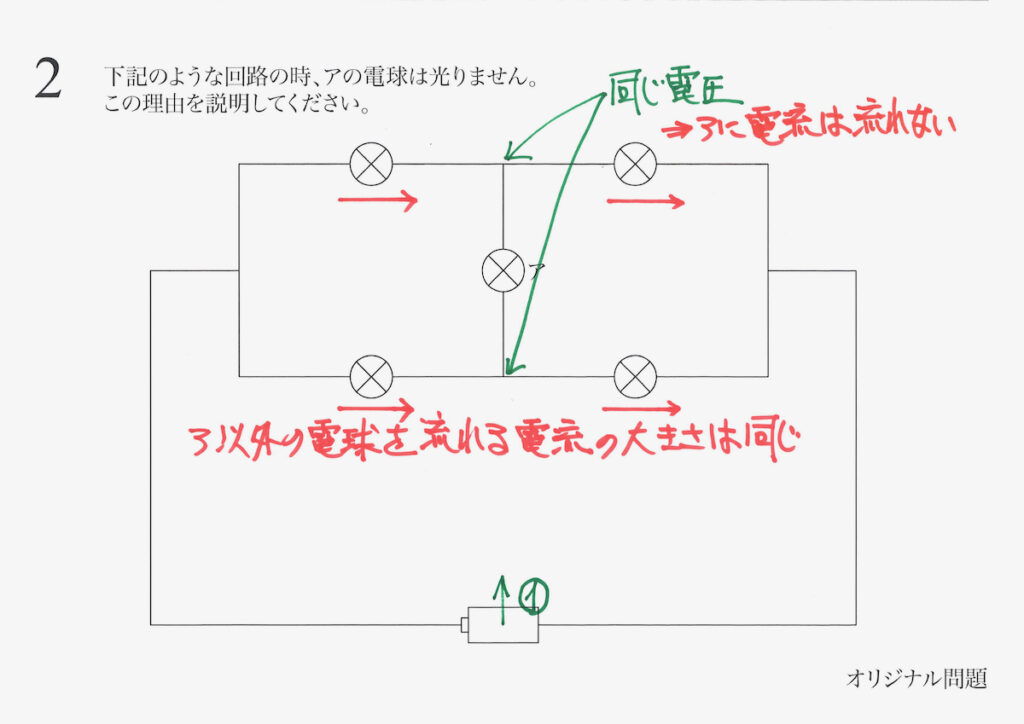
ここからは、電圧か電流を考えて「アに流れる電流は0」と分かります。

電球や抵抗の位置・数と対称性

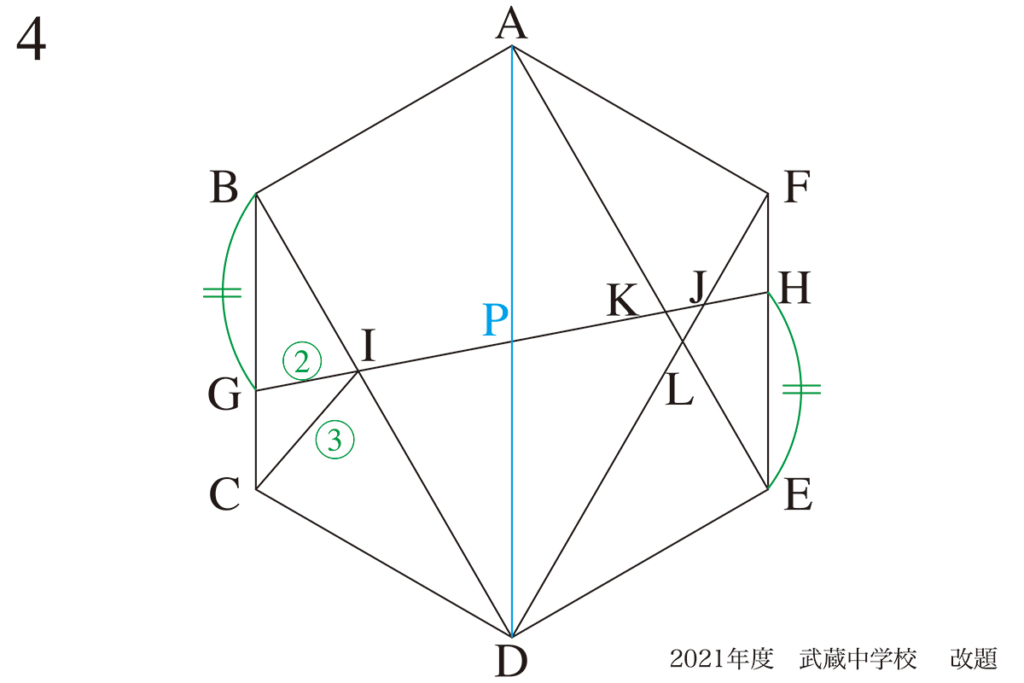
このように、理科や算数では「対称性がある図形・回路」に出会ったら、対称となる軸を考えましょう。

そして、「対称となるから・・・」と考えると、色々と分かるでしょう。

回路に関しては、対称性に注意することがあります。

それは、「対称となる」とは「回路全体を見て、ある軸に対して対称である」ことです。

そのため、回路の電線の形が同じでも「電球や抵抗の位置や数が異なる」と「対称性はない」です。

上の回路は全て「電線の形」同じで「対称性がある」のです。

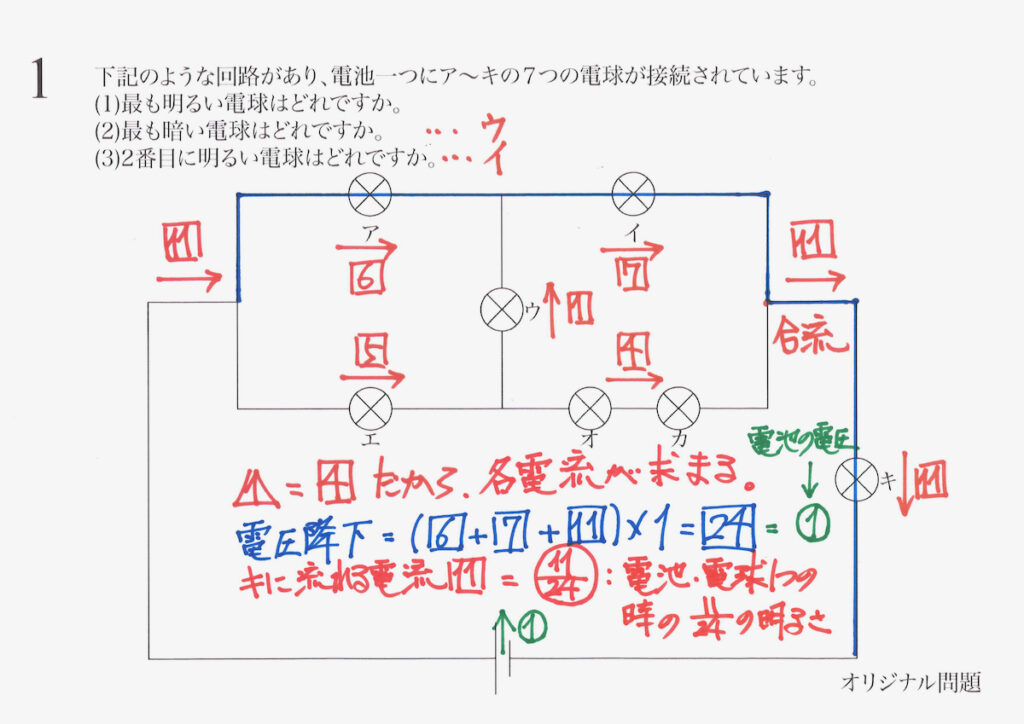
問題1の回路は、問題2の回路と「似ている回路」です。

ところが、電球の数や配置が「少し異なる」ために、流れる電流は全然異なります。

「電球・抵抗の位置・数が異なる」ので「対称性がない」時、全体的にバラバラな電流が流れます。

平面でも立体でも、「対称性がある」と「対称となる軸に対して同じ」になります。

色々と考えてみると、新しい発見があるでしょう。