前回は「電気・電流・回路の実戦的考え方 1〜回路を流れる電流を考える・法則を理解する姿勢・丸暗記・パターンでは「分かる」こと・記述・応用問題への対応・原理・法則の理解〜」の話でした。
回路の形と電球の配置：算数の問題と理科の問題は友達
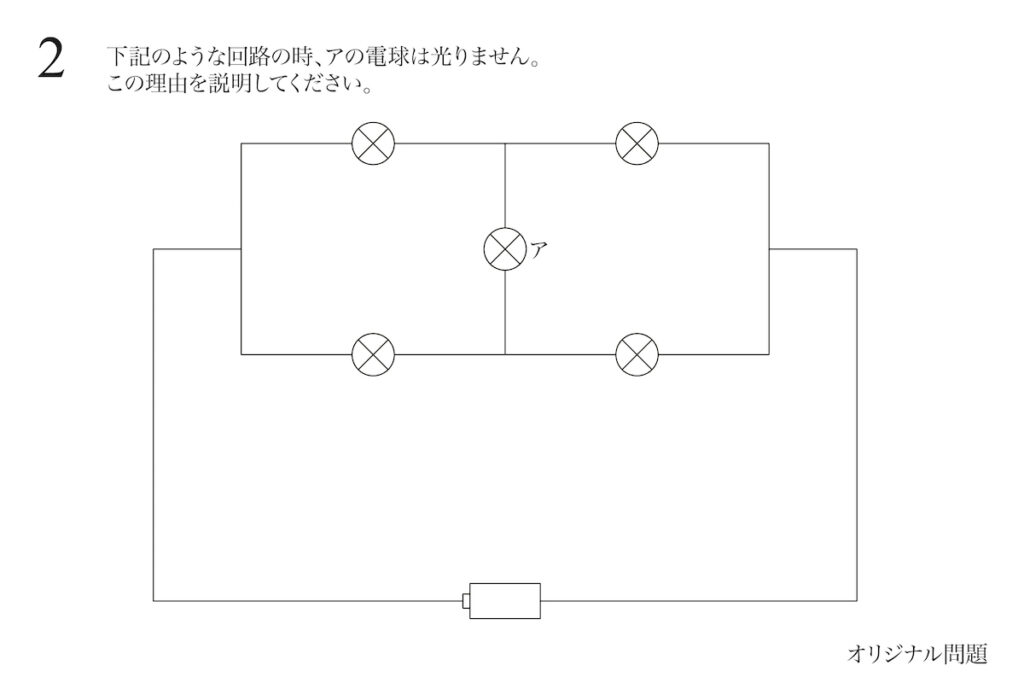
「電球の明るさ」などを問うことが多い、電気・電流の問題。
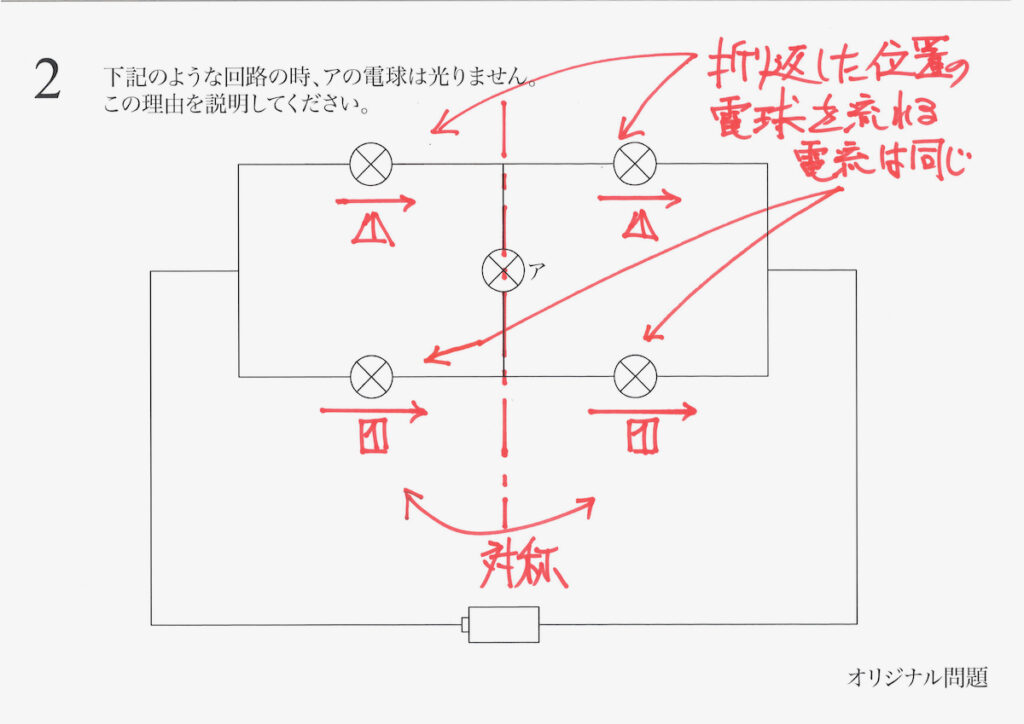
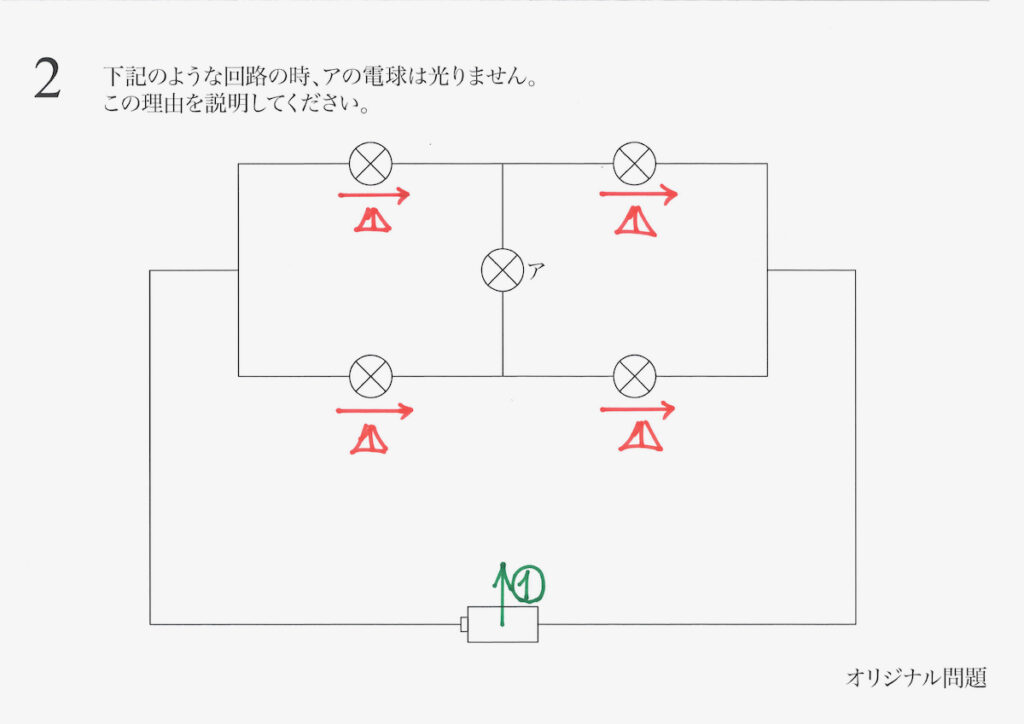
今回の問題は「アの電流が光らない」という事実が伝えられ、「その理由」を問うています。
同様の問題として、
出題者アの電流が光るか、光らないか、
答えてください。
出題者そして、その
理由を答えてください。
このような問題も考えられます。
いずれの場合も、電流・回路をしっかり理解する姿勢が大事です。
早速考えてみましょう。
塾講師こういう回路では、
ここの電流は0！
こう習っているかもしれませんが、基本をしっかり考えて「なぜ？」を考えましょう。
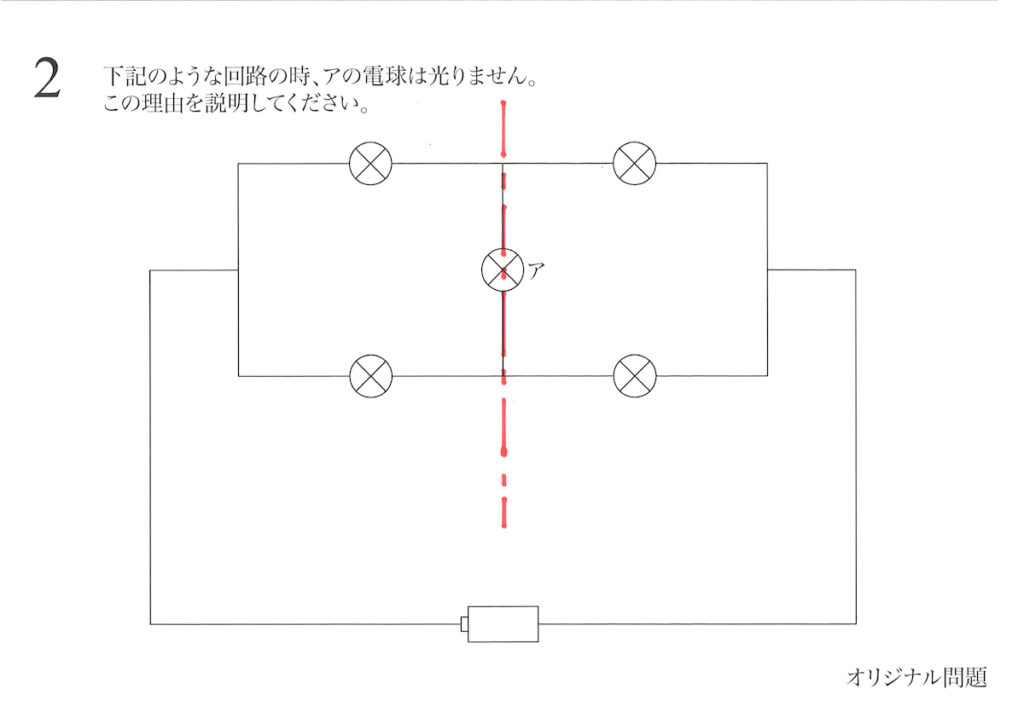
回路・電流の問題では、
男子小学生合成抵抗は
どのくらいだろう？
女子小学生ここの電流は
どう流れるだろう？
すぐに電流と抵抗に考えがゆく傾向があります。
回路を流れる電流を考えるときは、「まずは電圧」を考えることが大事です。
「主役は電圧」の話を、上記リンクでご紹介しています。
今回の回路では、「電池一つ」なので、「電圧を発生させる元は一つ」です。
上の図のように、回路に赤い線を入れてみました。
男子小学生あっ、折り返しても
同じだ。
女子小学生回路が
対称だね！
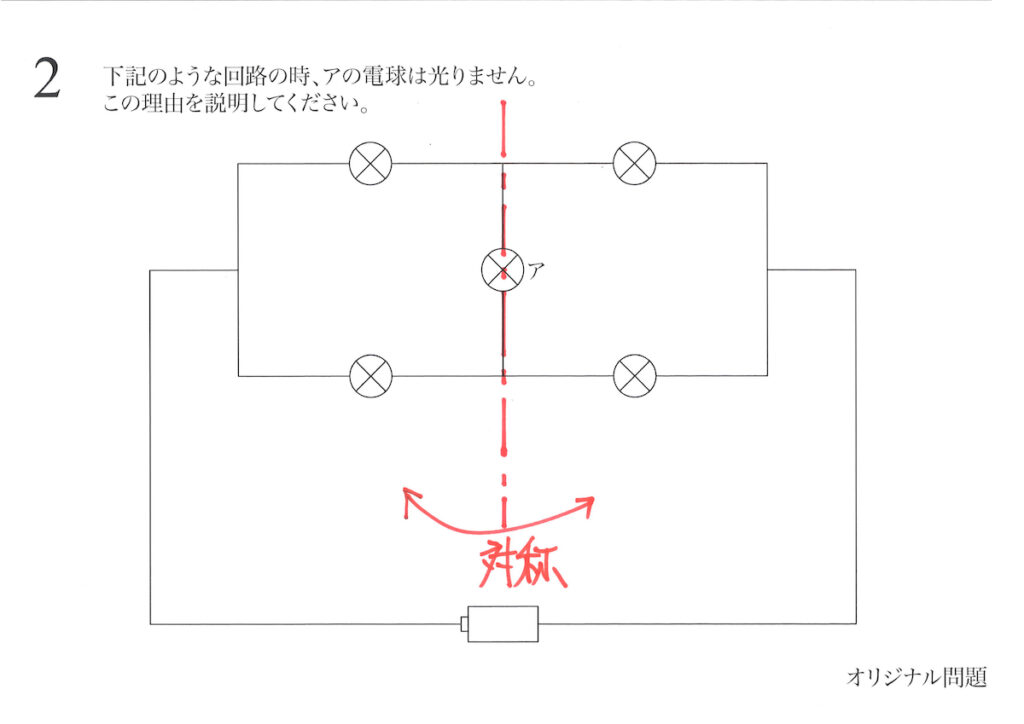
回路が「左右で折り返して同じ」で対称です。
対称性がある図形としては、正三角形・正方形・長方形・円などがあります。
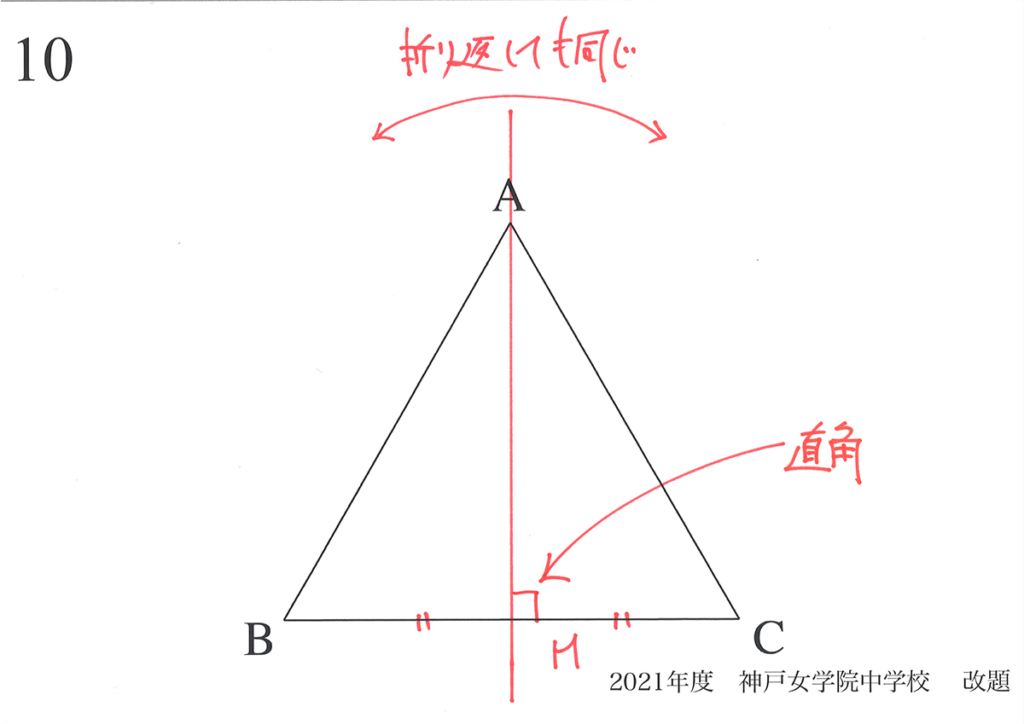
正三角形の対称性に関する話を、上記リンクでご紹介しています。
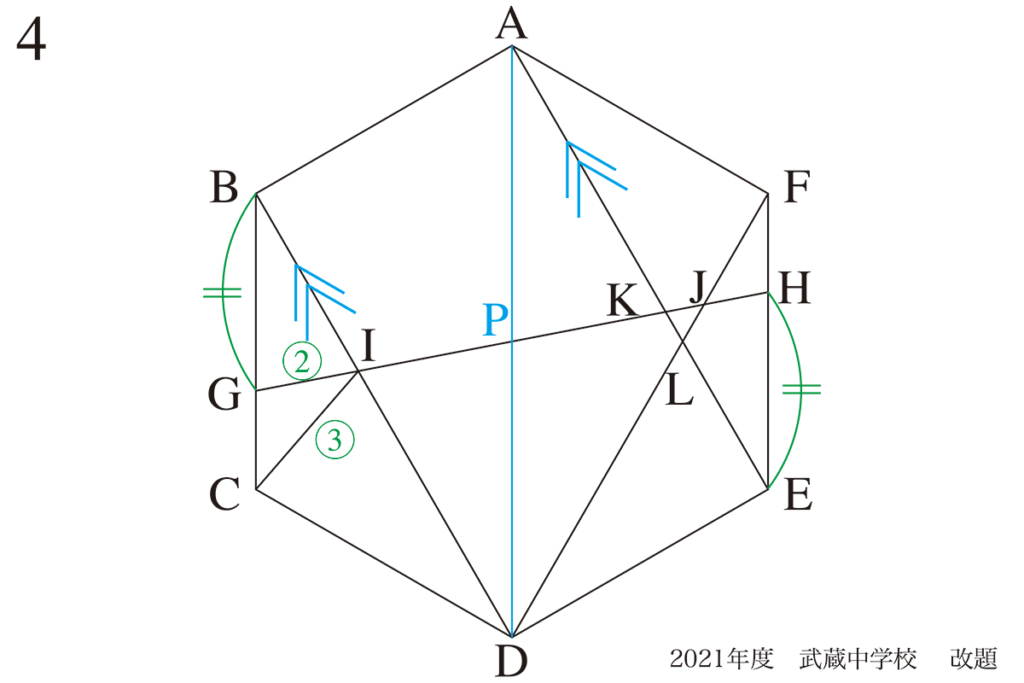
また、正六角形も対称性を持ちます。
「対称となる軸」や「中心・重心」は図形において、非常に大事です。
男子小学生これは理科の問題だけど、
算数っぽいね・・・
女子小学生理科と算数が
混ざった感じで、不思議・・・
算数の問題と理科の問題は「お友達」であることが多いです。
今回は、「算数の図形問題」と「理科の電気の問題」に類似点があります。
対称性があること：形と図形に安定感
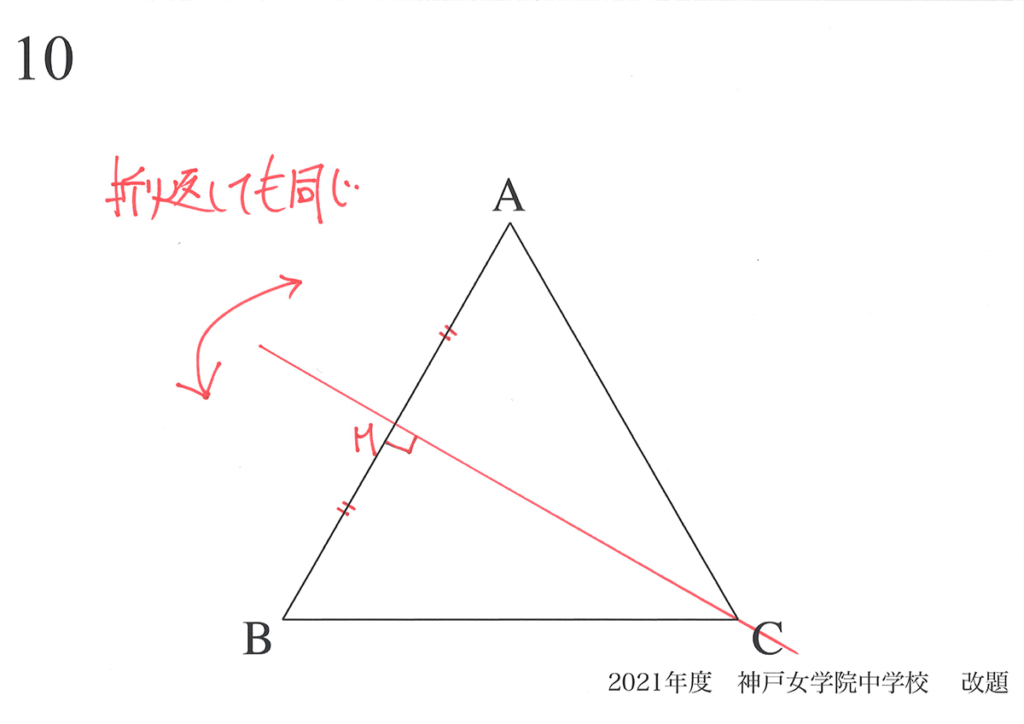
算数の図形問題で大事な「対称性」は、理科においても、とても大事な性質です。
世の中には「対称性があるもの」が、意外と沢山あります。
みなさんが座っている机や椅子も、「折り返したら同じ」で対称性があるでしょう。
あるいは、電車や車も「どこかの軸で折り返したら同じ」です。
この時、製造過程などで生じる誤差は考えずに、「基本的な形」で考えます。
なぜ、身の回りのものに「対称性があるもの」が多いのでしょうか？
男子小学生確かに対称性があるものが多いけど、
なんでだろう・・・
女子小学生対称性は知っているけど、
「なぜ対称？」は考えたことがないわ。
様々な理由がありますが、「対称であること」は非常に安定しています。
男子小学生確かに
そうかも・・・
女子小学生「左右で同じ」だと、
しっかりして見えるね！
「対称性があること」は、「安定感があること」です。
そして「対称となる軸に対して、同じ」です。
算数・理科において、「対称性があること」から分かることがあります。
上の図のように、「対称となる軸に対しては、流れる電流が同じになる」のです。
男子小学生えっ。
本当？
女子小学生なんだか、
不思議ね・・・
「折り返して同じ」となる対称性のある図形の回路。
ならば、流れる電流もまた「折り返して同じ」になるのです。
男子小学生確かに、
そんな気がしてきた。
女子小学生言われてみたら、
そうかもね・・・
厳密に「なぜ？」は難しいかもしれませんので、「そんな気がする」くらいで良いでしょう。
対称軸に対して同じ位置の「電流の値」を未知数でおいて、計算してみても、結果が出ます。
「左右で同じ電流」なので、二つの電流を未知数として置いてみましょう。
・どこかの面・線・点で折り返したら「同じ」形・図形になる
・形・図形が「同じ」時は、他にも「同じもの」がある
・安定感がある
点から点の下がる電圧・電圧降下
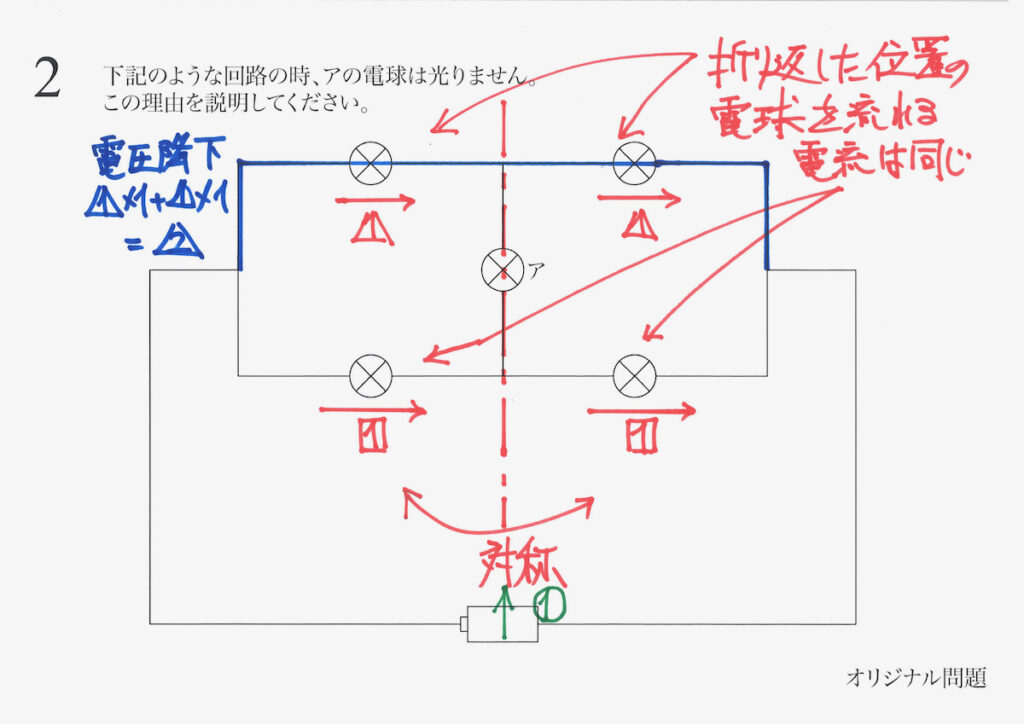
それぞれの電球の抵抗を「1」とします。
ここからは、下がる電圧=電圧降下を計算しましょう。
電気・電流・抵抗のある回路では、必ず「ある点からある点の電圧降下が経路によらず同じ」です。
電池が電圧をかけて、「エイッ」と電流を持ち上げて「流れる」のが電流です。
持ち上がった電流が、電圧降下で下がった時。
「下がる高さが異なる」と「合流できない」ので困ってしまいます。
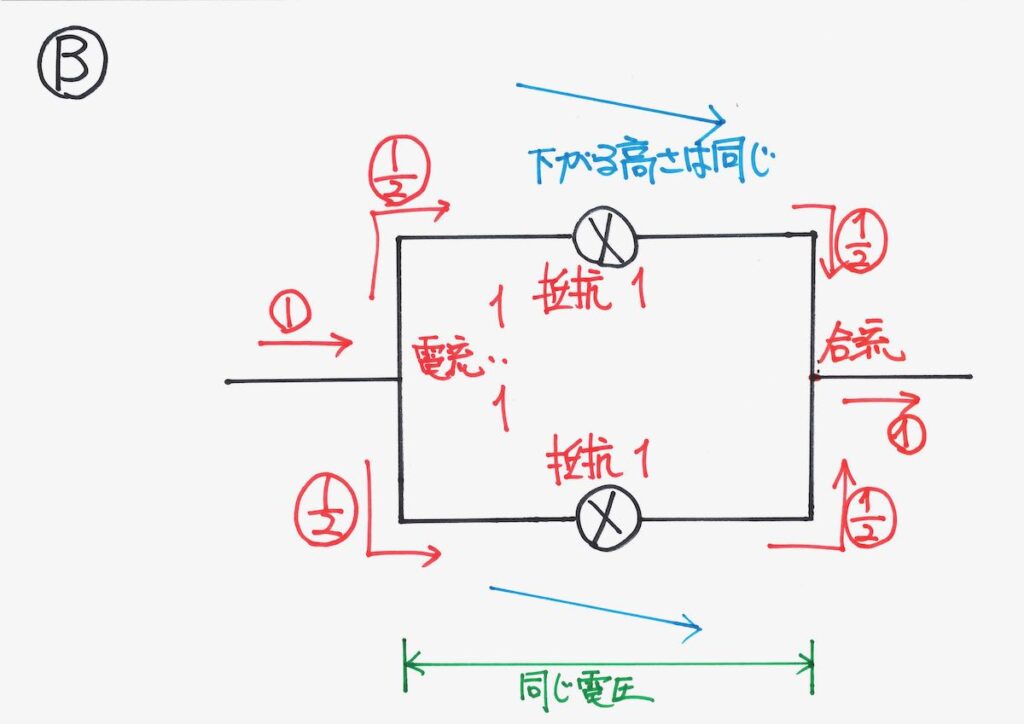
この「ある点から点で、下がる電圧は同じ」をしっかり理解・イメージすることが大事です。
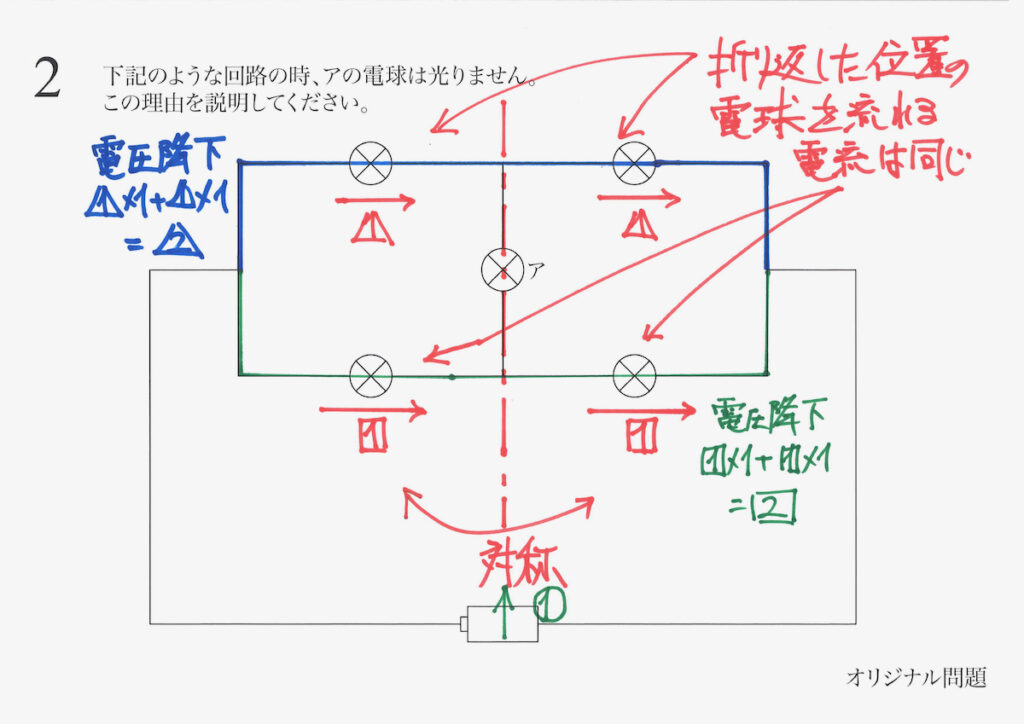
青色と緑色の経路での電圧降下を「電流x抵抗」で計算します。
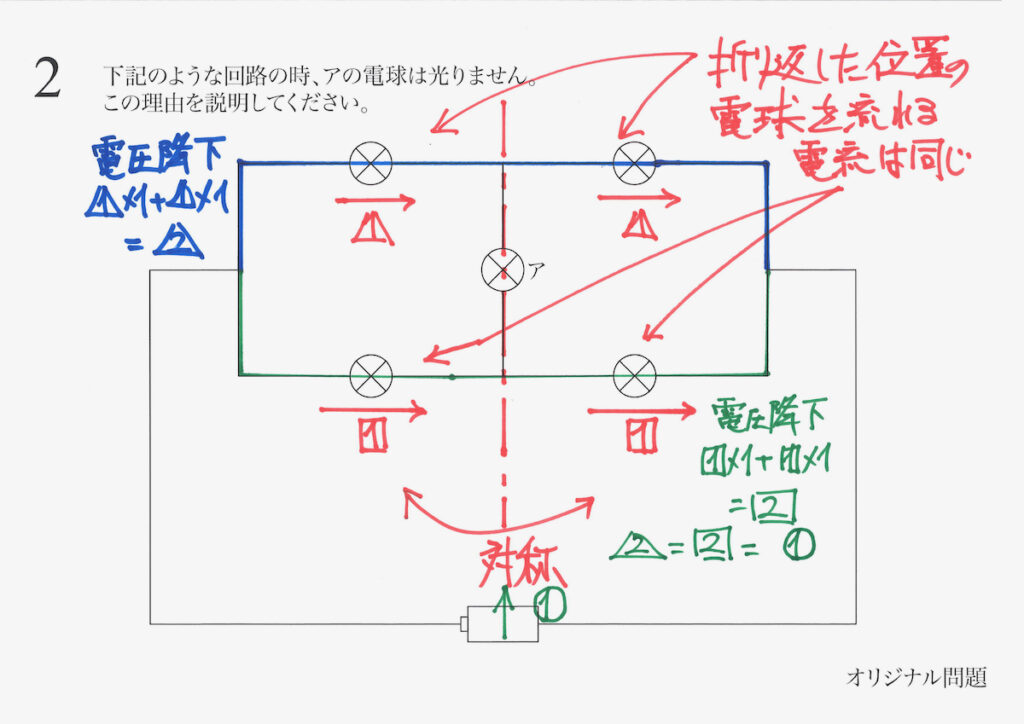
これらの電圧降下が同じなので、考えていた電流の大きさは「実は同じ」でした。
男子小学生計算してみたら、
分かったね・・・
女子小学生こうして、計算して
何か分かるって楽しい！
ここまでで、上記のような状況まで分かりました。
理科・算数では、「分かったことを一度整理」することも大事です。
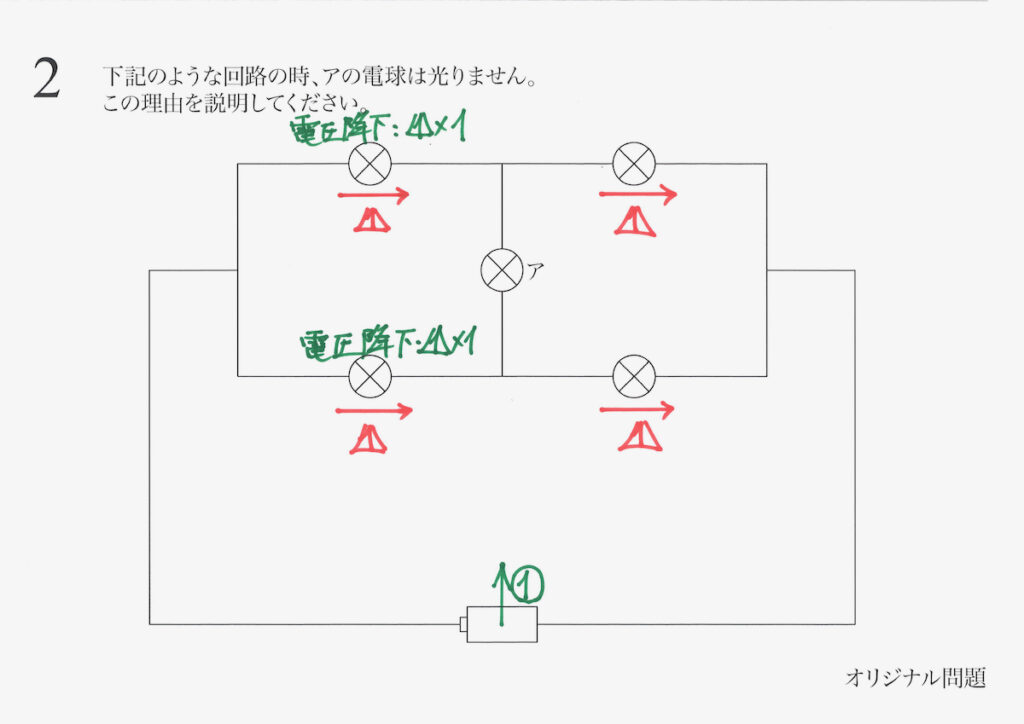
電池によって電圧がかかって、電球（抵抗）で電圧が下がります（電圧降下）。
この時、電圧が下がる過程で「電力が消費されて、電球が光る」のです。
この「電力が消費」を「消費電力」と呼び、詳しくは中学・高校で学びます。
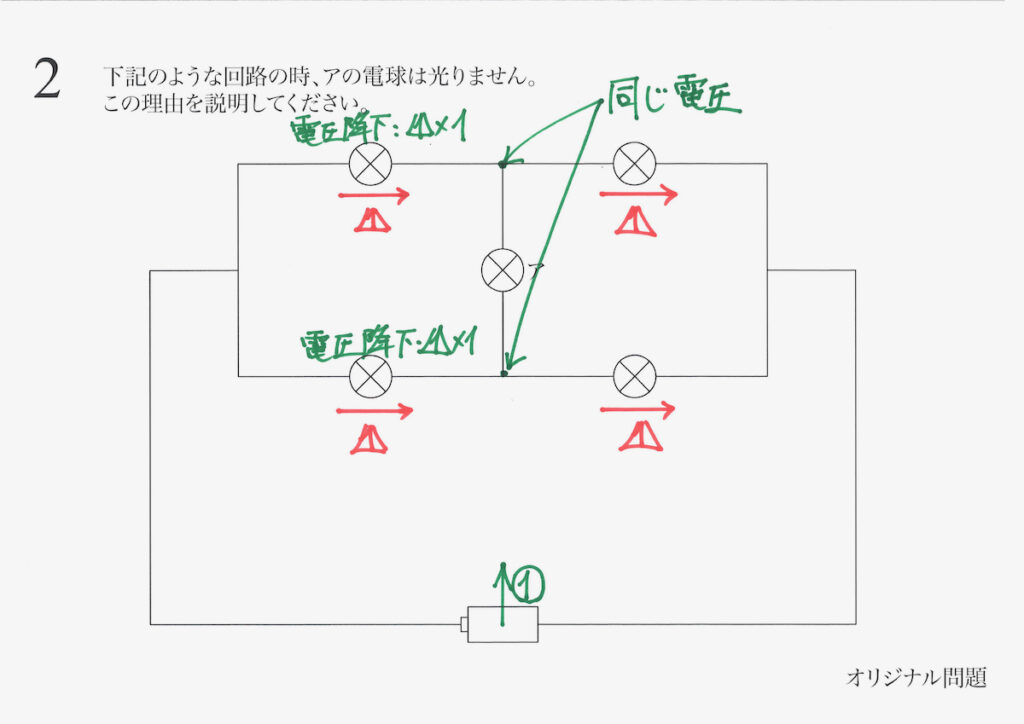
すると、アの電球の両側（図の上と下）では、「下がる電圧が同じ」です。
「元の上がる電圧=電池が同じ」なので、アの電球の両側では「同じ電圧」となります。
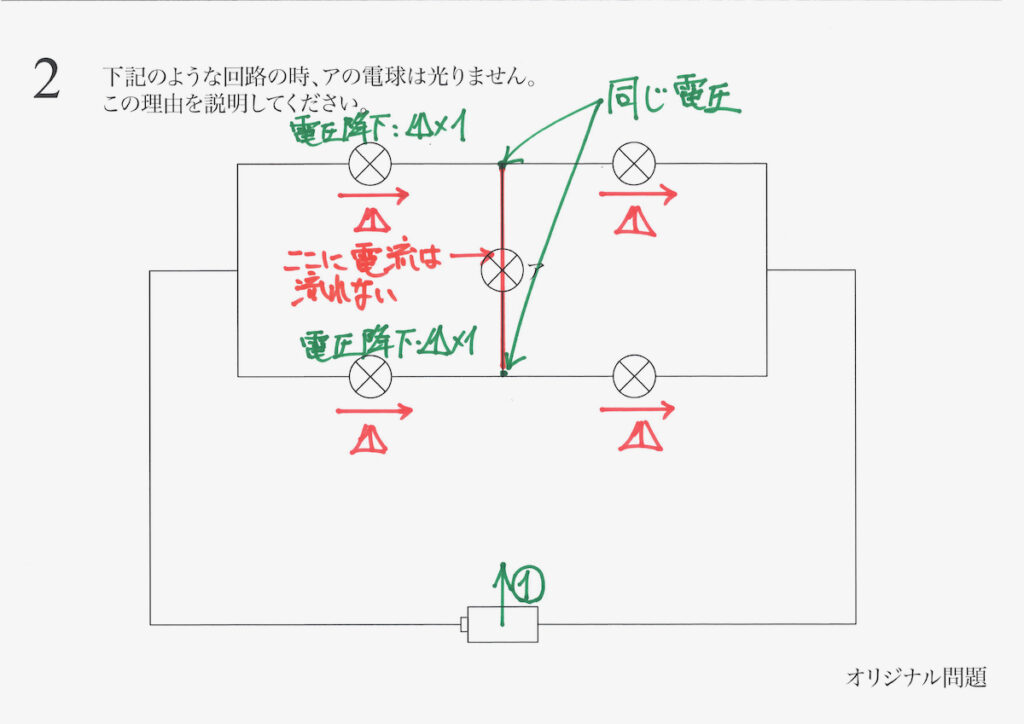
「両側が同じ電圧」では、電気の流れません。
それは、電流は「両方同じ電圧だと持ち上がらない」からです。
・アを通る電線の両端が同じ電圧だから
「エイッ」と「持ち上げてくれる電圧」がいないと、電流は流れないのです。
やっぱり、
電圧が大事なんだね・・・
電圧があって、電流が流れる
イメージが、より分かってきた！
未知数を設定して考える
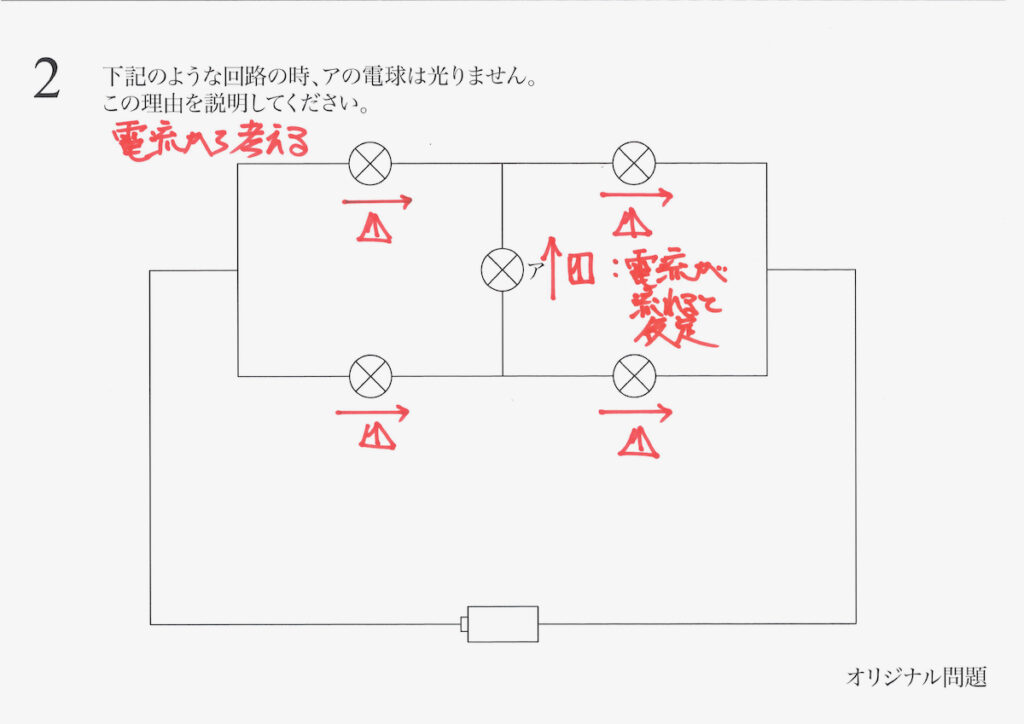
仮に「電気が流れる」と考えると、考えてみましょう。
男子小学生もう、ここには「電流は0」って
分かったから、いいんじゃない？
「もう分かった」のですが、「別な視点」で考えてみましょう。
理科や算数では、「別な視点」「別解」を考える思考は総合力を高めるでしょう。
アを流れる電流の大きさを、設定します。
今回は、電圧ではなく「電流から考える」をしてみましょう。
男子小学生いつも、
電圧が最優先じゃないの？
「主役は電圧」ですが、「脇役の電流」も時には「考える主体」になります。
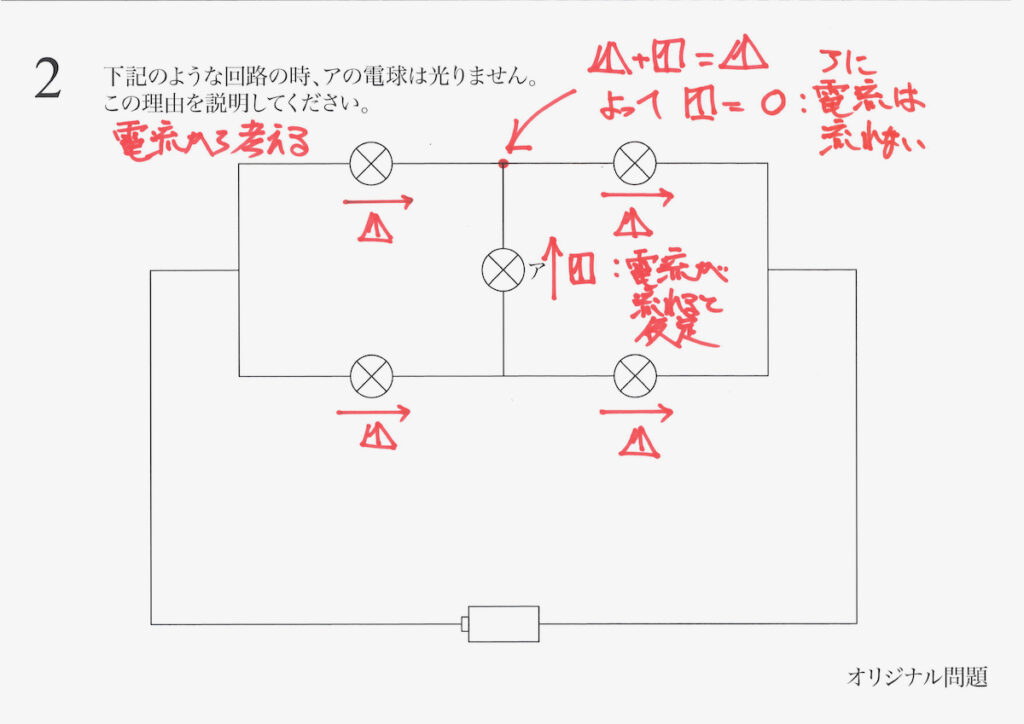
上の点で「電流が合流する」ので、電流が計算できます。
その結果、「アを流れる電流は0」と分かります。
「両側（両端）に電圧の差がないから、電流は0」とパッと分かることも大事です。
このように、「計算してみたら分かる」ことも大事です。
基本的なことをしっかり考えるようにすれば、物理の問題は解けるようになります。
基本をしっかりと考えたので、少し遠回りに感じるかもしれません。
電気・電流を分かっている方は、もう少し途中を飛ばして考えても良いでしょう。
今回は対称性を考えましたが、次回は「計算して解く」考え方をご紹介します。
次回は下記リンクです。
