前回は「電気・電流・回路の分かりやすい考え方 1〜電圧が主役・電圧が電流を流す根源の力・回路と回路の間の電線・分かれる電流のイメージ・流れる電流を描いてイメージ〜」の話でした。
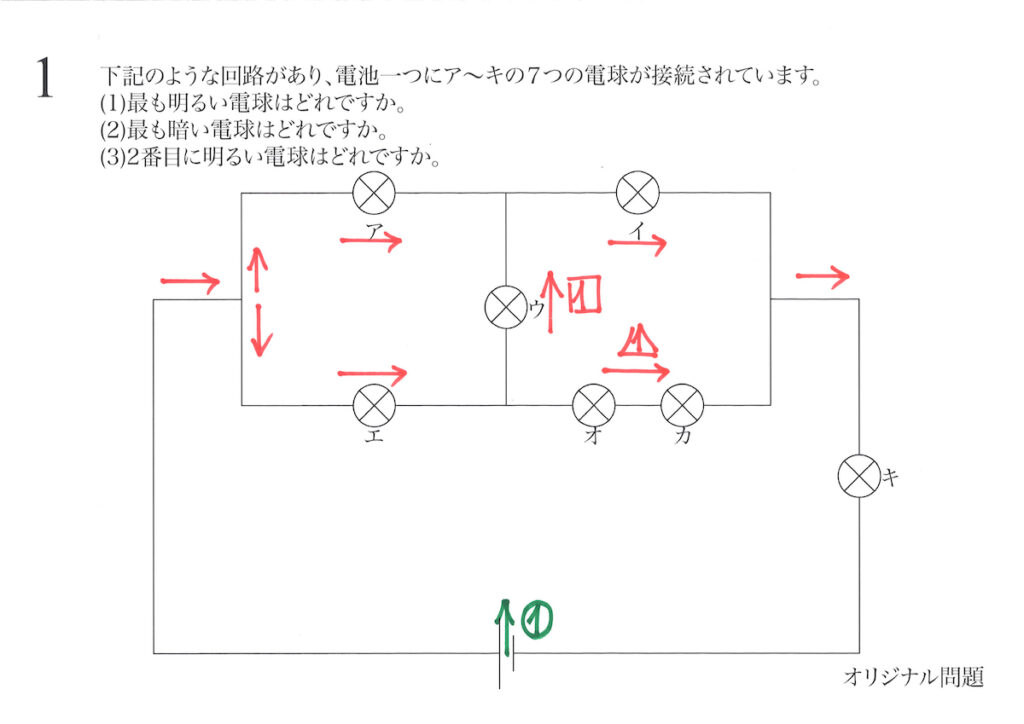
問題 1(再掲載)
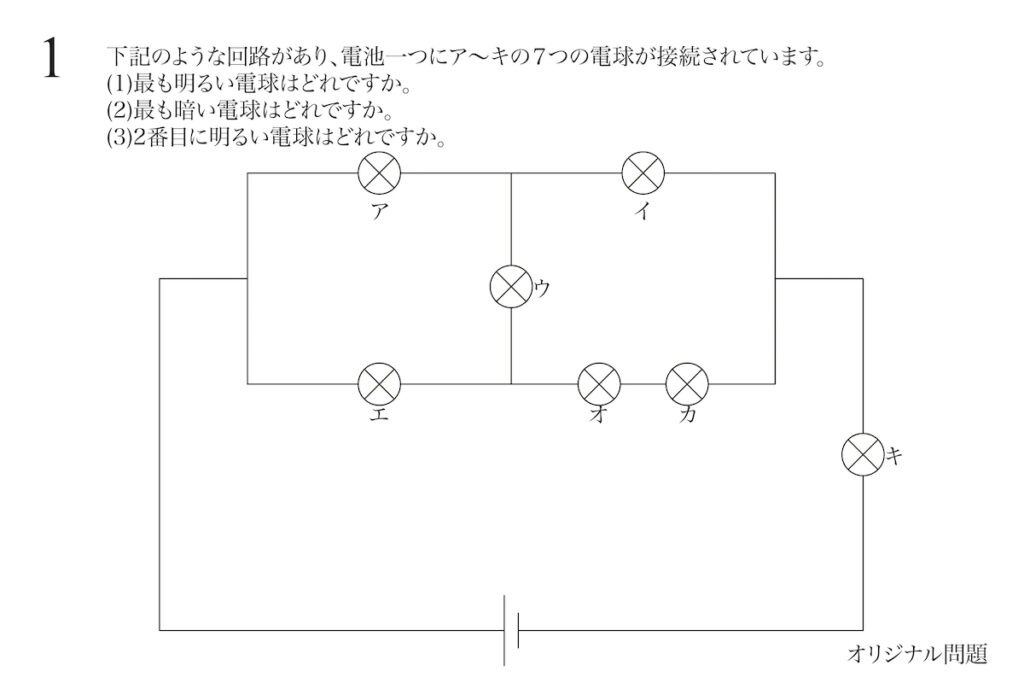
シンプルな問題ですが、今回は(1)から考えてゆきましょう。
電気・回路の問題は、「回路のパターンを暗記して、合成抵抗を考える」解き方でも解けます。
志望校の出題傾向によりますが「理科の小問が多い」場合は、その方が「早く解ける」でしょう。
一方で、記述式を含む「応用問題の傾向が強い」出題傾向の場合、原理を理解することが大事です。
 男子小学生
男子小学生電圧が主役で、
電流が流れる、だよね!
てこ・かっ車・ばねなどの問題も「様々な問題を作れる」のと同様に、回路も「様々作れる」のです。
さらに、てこ・ばねなどよりも「回路の方がバリエーションを作りやすい」傾向があります。
それは、「回路は電線をつないだり、複雑にすれば」複雑な回路が作れるからです。



確かにそうかも・・・
前の模試でも少し変わった回路があった・・・
中学受験では「立体化された回路」が出題されることもあります。
「平面的な回路」と「立体化された回路」では、「立体化された回路」の方が難しく感じられます。
ここで「基本原理は同じ」であることを、はっきりイメージしましょう。
回路に流れる電流を描いて考える:電池一つの電圧で電流=①
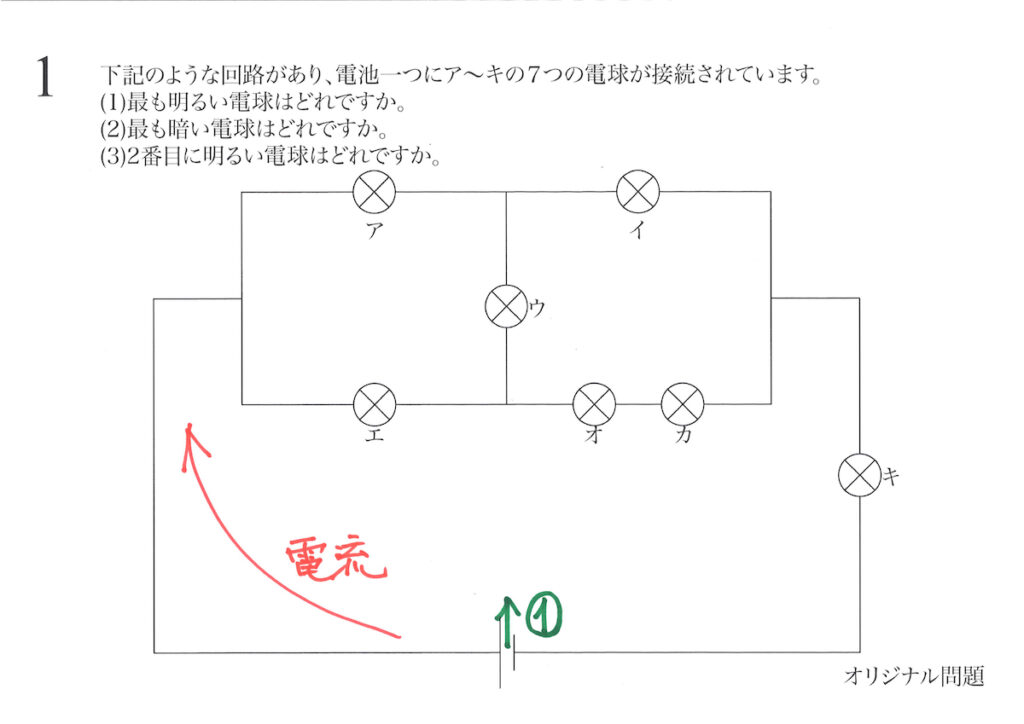

電池で電圧がかかり、回路に電流が流れてゆきます。
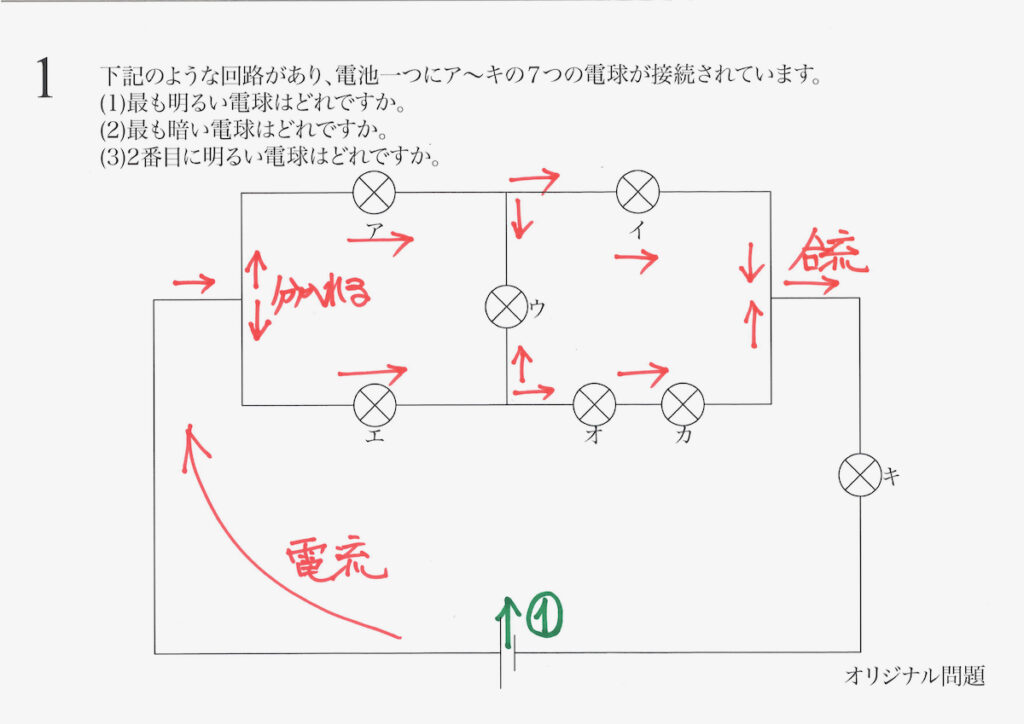

電線が別れているところは、原則として電流が別れます。
そこで、「流れる電流」を描いてゆきましょう。



こんなにたくさん電流が
分かれると、難しい・・・
「別れた電流」は、電線がつながるところで合流します。
「たくさんある電流」は、「同じ電流」もあるので、一つ一つ考えてゆきましょう。
上記のような流れは、電気・電流・回路を「ある程度理解」していると「当然」に感じられます。
試験本番では、全部は描かなくても良いですが、勉強している時は描きましょう。
こういう「流れ」や「力」は、実際に矢印で描いてみると、イメージが湧きます。
「頭で分かっている事」も大事ですが、このように「具体的に描いて理解」することも大事です。
そして、「電池・電球が各一つ」の基本的な回路に対して、「電圧を①、抵抗を1」と考えます。
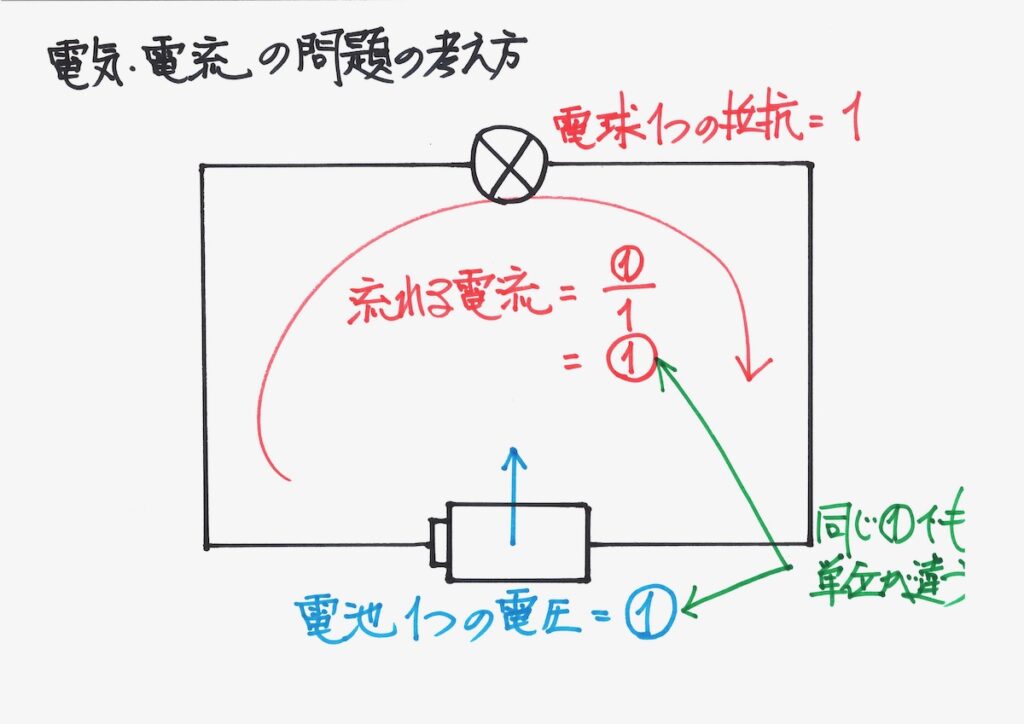

電池一つによって「エイッと電流を持ち上げる」電圧=①と考えましょう。
・回路に電圧を発生させる
・発生した電圧は、電流を持ち上げるポンプの様な役割を持つ
・「電池=電圧=ポンプ」が回路にあるイメージ
そして、電球一つの「抵抗=1」と考えます。
流れる電流も①となることを「比較する大きさの基本」として考えましょう。
この時「流れる電流=電圧=①」となりますが、「同じ量」ではなく単位が異なります。
単位は理科・物理では非常に大事ですが、問題を解く時は気にしすぎないで良いでしょう。
・電圧 = 電流 x 抵抗(オームの法則)
・主役は電圧
・「電池 = ポンプ」が回路に電流を流す
・回路を流れて、一周した電流は「上がった高さ」分下がる(電圧効果)
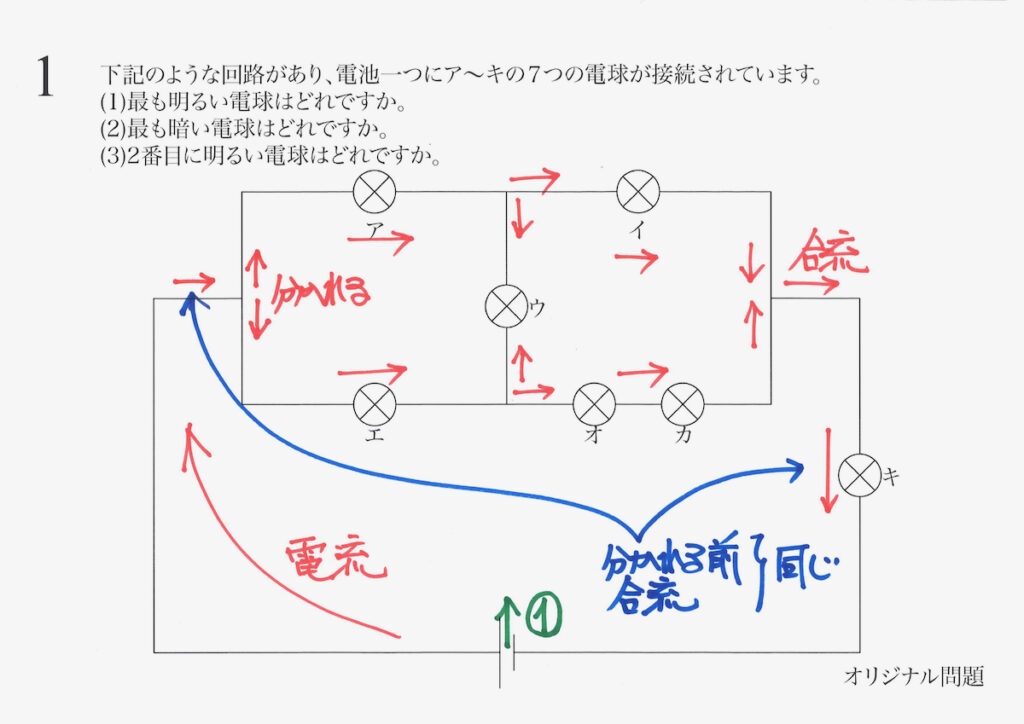

最初に「別れる前の電流」と最後に「全てが合流した電流」は同じです。



うん。これは
分かるよ!
このように、「少しずつ不明(分からない)電流の正体」をつかんでゆきましょう。
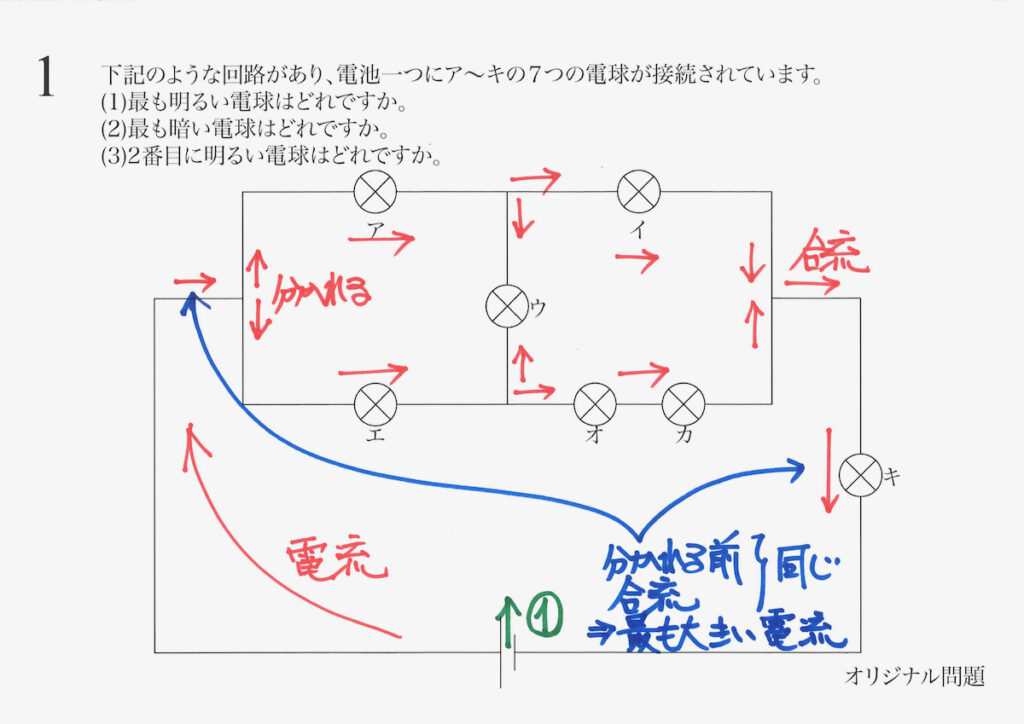

他の「別れた電流」よりも、これら「最初と最後」の電流は最も大きい電流です。
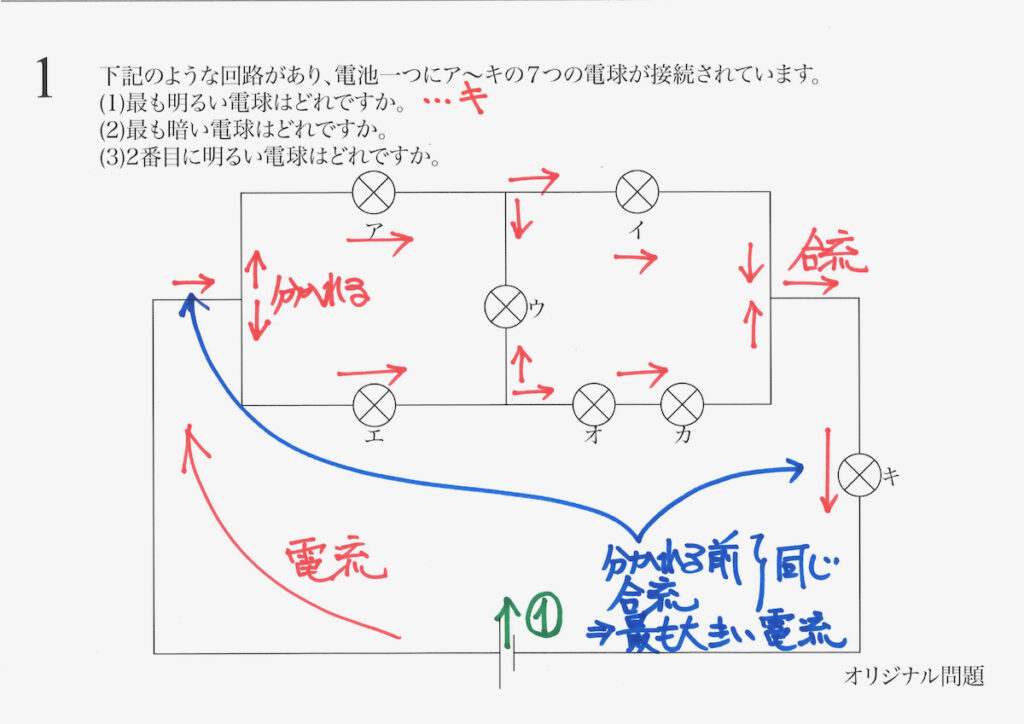

そこで、最も大きな電流が通る「キの電球」が最も明るくなります。
(1)の答え・・・(キ)です。
・最も明るい電球は、最も電流が大きい(キ)
分かれる電流はどちらに流れる?:電流同士が衝突?
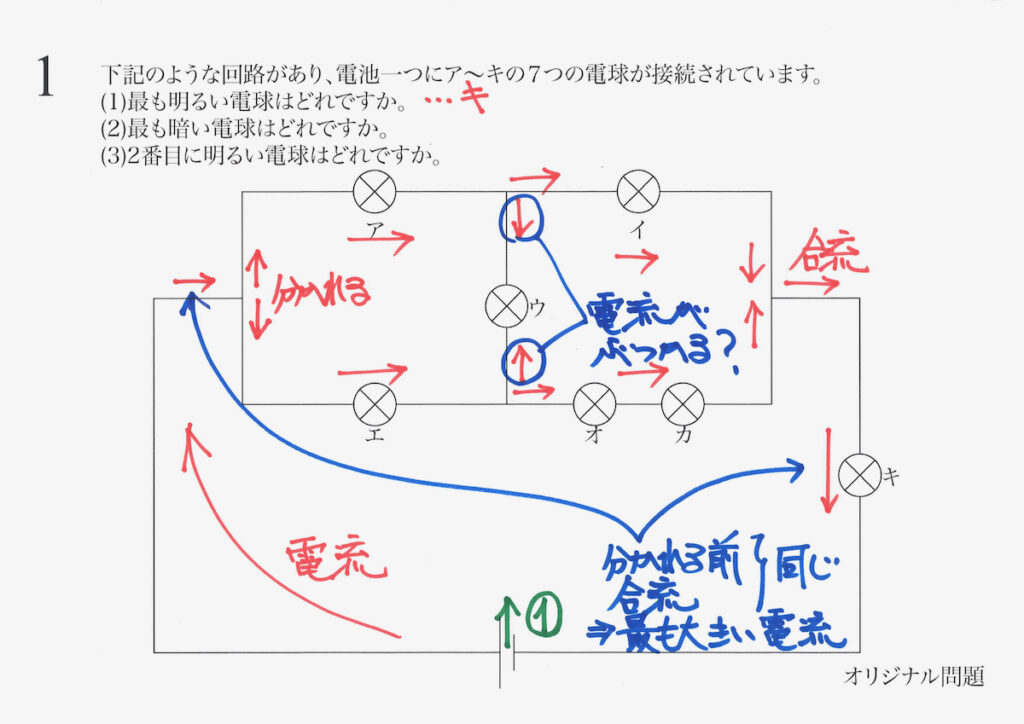

途中で電線が繋がっているウの電球には、上の図で上からと下から電流がきます。



これでは、
電流同士がぶつかってしまうけど、いいの?
「電流がぶつかる」イメージです。
実際には電流は「どちらかにのみ流れる」ので、向きがあります。
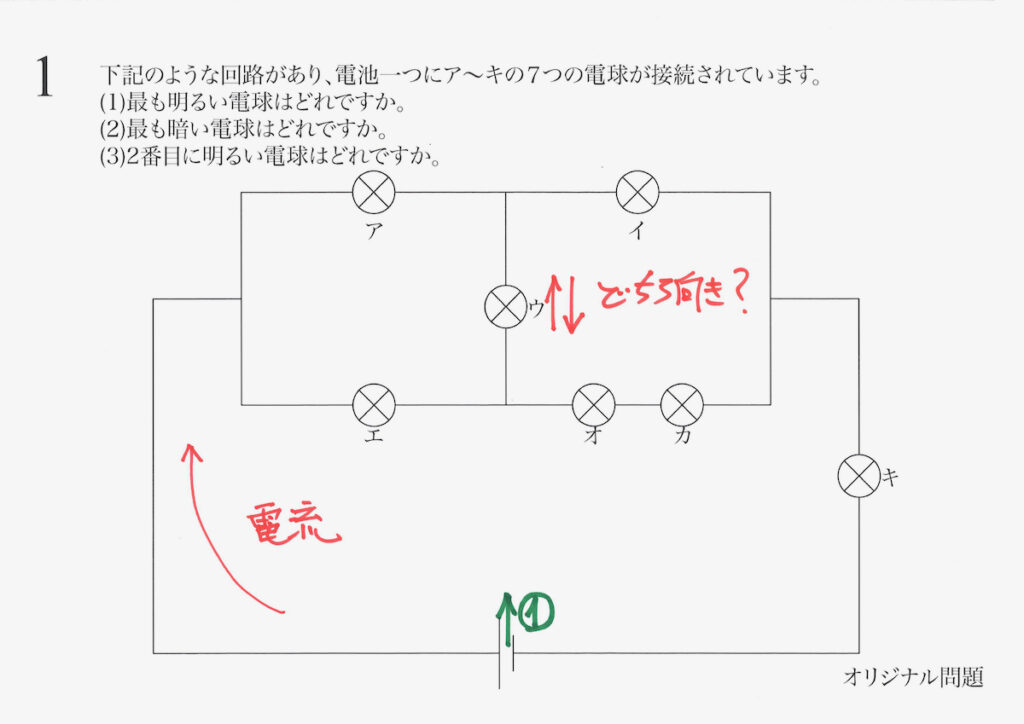

どちら向きに流れるでしょうか?



どっちかな・・・
分からないけど・・・
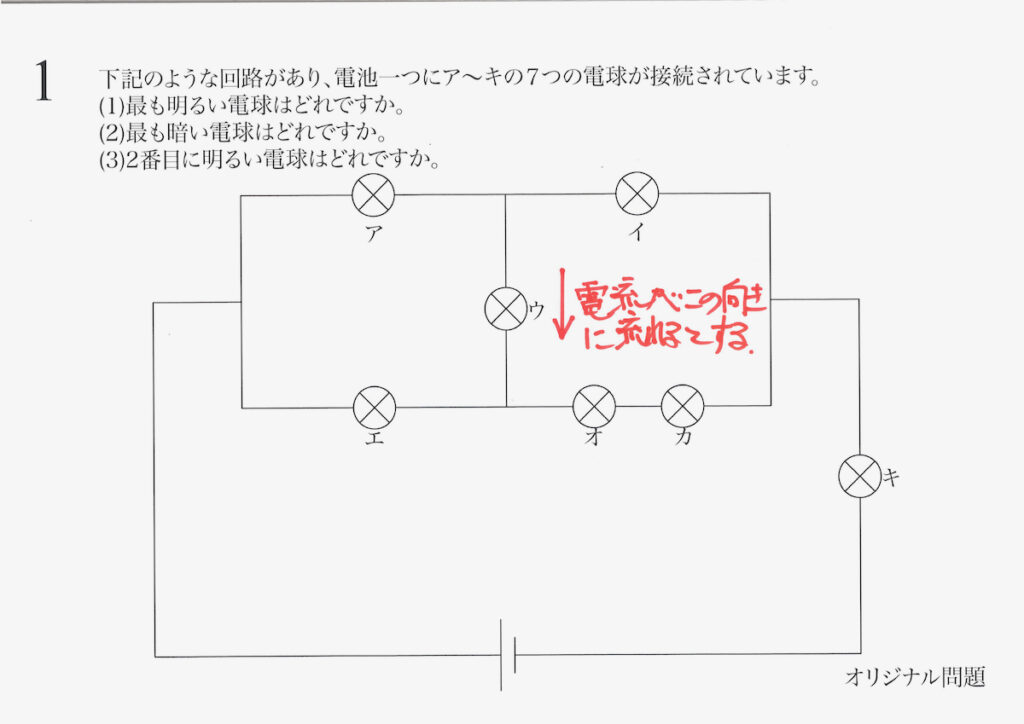

上の図のように、ウに対して下向きに流れるとして、考えてみましょう。



勝手に決めて
いいの?
これは「仮に下向きと考える」のであり、理科では「仮に考える:仮説を立てる」ことは大事です。
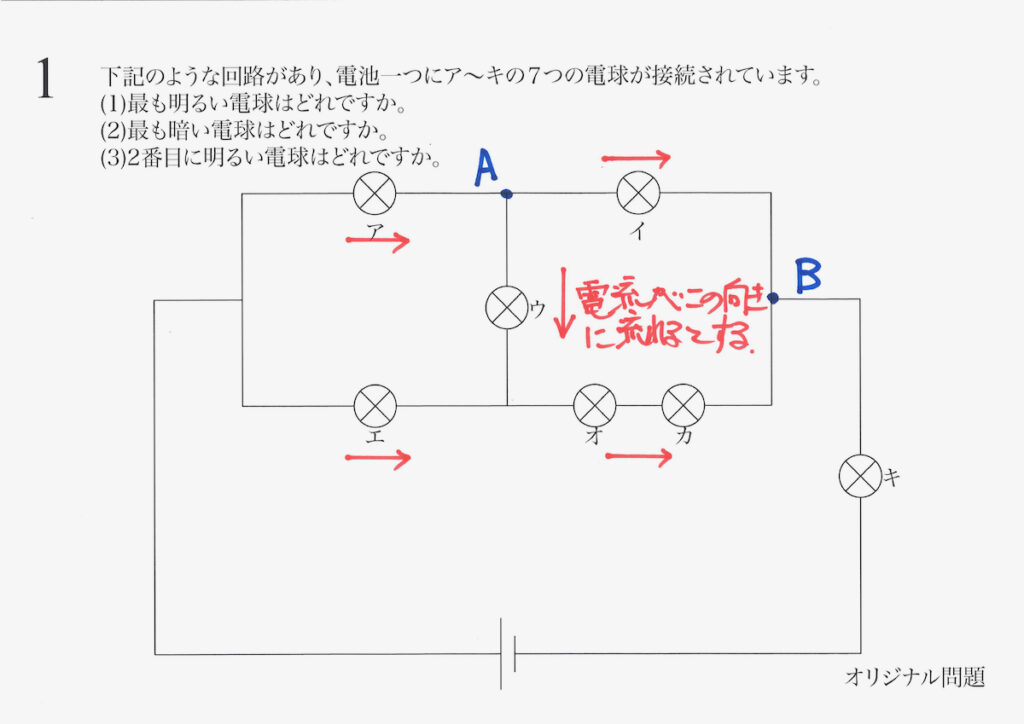

この時、ウの電流の周辺の電流を考えてみましょう。
上の図のA、Bにおける電圧の大きさ(電位)を考えます。
Aから「イを通ってBへ」流れる電流と、Aから「ウ→オ→カを通ってBへ」流れる電流を考えます。
この時、両方の経路において、電球があるので抵抗を受けて、電圧が下がります。
そして、その下がる電圧の大きさは同じです。



確かに、
ここで下がる電圧は同じはずだね。
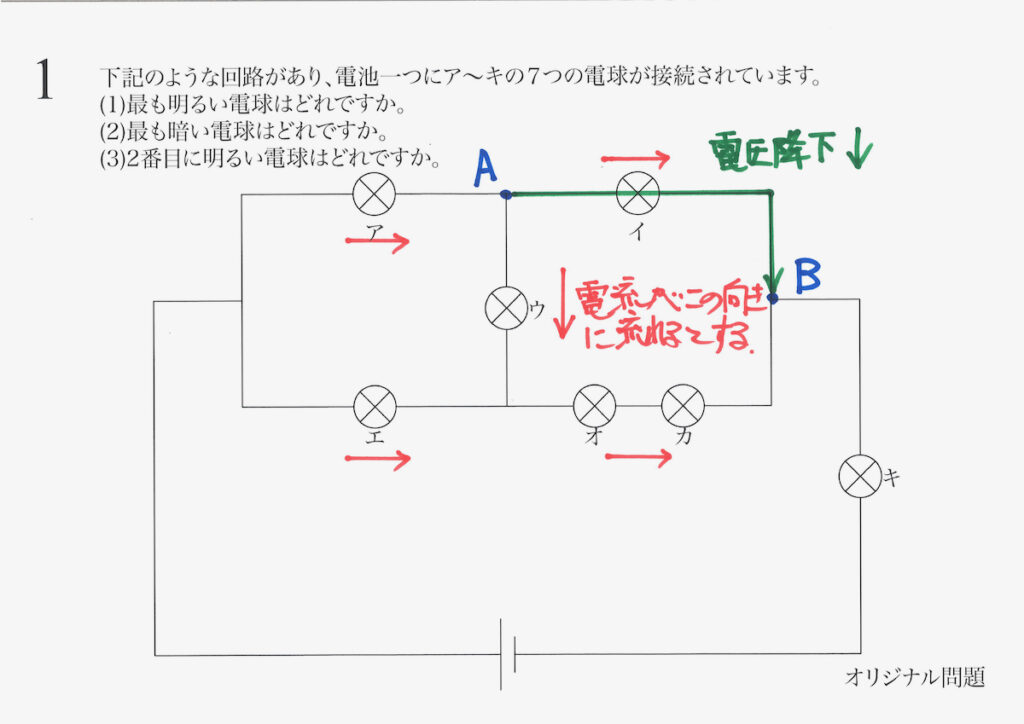

まずは、前の緑色の経路を考えてみましょう。
ここでは、イの電球による抵抗を受けて、電圧が下がります(電圧降下)。
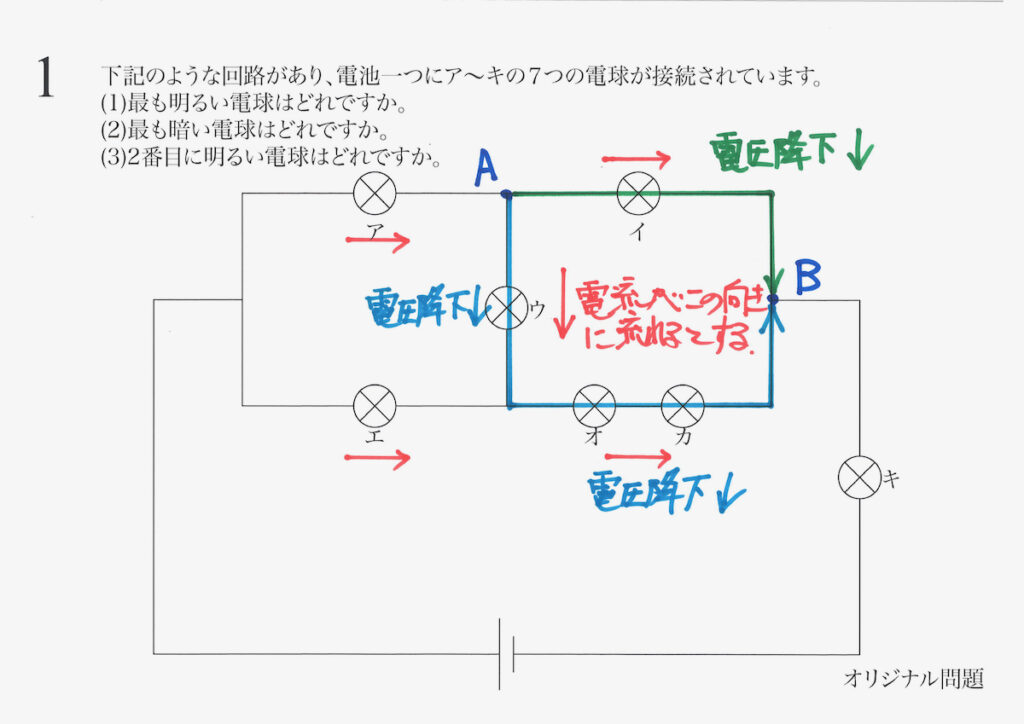

今度は、後の水色の経路を考えてみましょう。
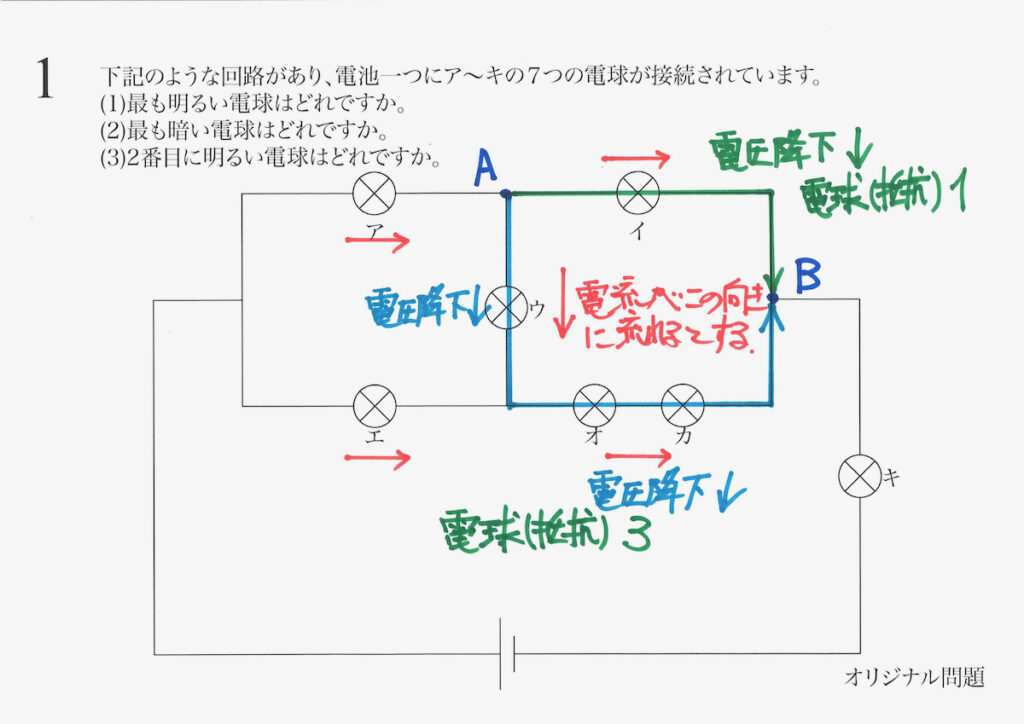

「ウ→オ→カを通ってBへ」流れる電流は、三つの電球による抵抗を受けます。
そして、「それぞれの電球で電圧が下がる」ことになります(電圧降下)。
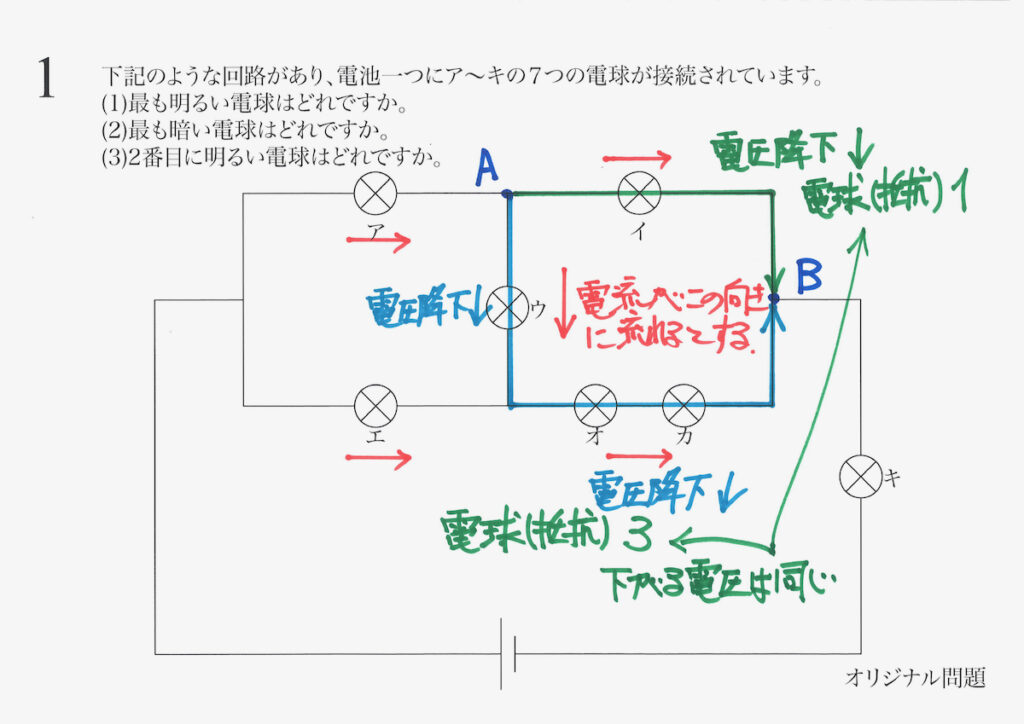

緑色の経路、水色の経路における、電圧の下がる大きさ(電圧降下)は同じです。
緑色を流れる電流の大きさが、水色を流れる電流の大きさより、だいぶ大きければ成立します。



そんなに流れる
電流の大きさが違うかな・・・
この回路で、緑色と水色の電流の大きさは、それほど大きくは違わない感じです。
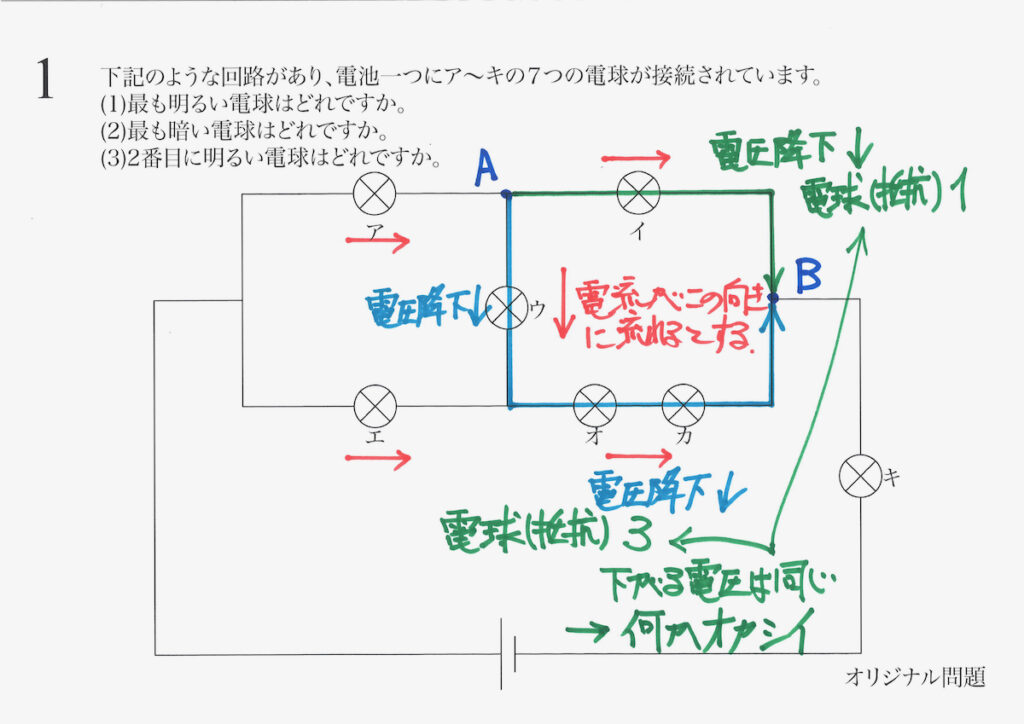

そこで、



これは、ちょっと
オカシイかな・・・
「オカシイかな」と感じるでしょう。
「ちょっとオカシイかな」と感じることは、大抵「オカシイ」です。
理科の物理分野は、基本的には日常生活と密接に繋がりがあります。
実際に「ちょっとオカシイ」と感じることは起こらないことが多いです。
現実的には、「計算しなければ分からない」ことも多いです。
ここでは、「オカシイ」ので、「ウを流れる電流が、図で下から上向き」になります。

そこで、「ウを流れる電流が、図で下から上向き」と考えましょう。
そして、「ウを流れる電流」と「オ、カを流れる電流」を、それぞれ未知数を置いてみましょう。
未知数の置き方は、さまざまな考え方があります。
「全体から見る」考え方と「部分から見る」考え方があります。
「どちらが良いか」は、問題にもより、そして個性にもよるでしょう。
電流の問題では「全体の電流を未知数」として、考えることも出来ます。
その場合、抵抗を考慮して「全体像を見てゆく」ことになります。
この回路はシンプルですが、電線の分岐が多いので比較的複雑です。
そこで、「別れた先の電流を未知数」として考えてみます。
ここからは「電流の分かれ・合流」と、先ほどの「ある点から点で、下がる電圧が同じ」を考えます。
地道に少しずつしっかり考えることで、電気・電流の問題は解けるようになるでしょう。
次回は下記リンクです。


