前回は「文章題のてんびん算を解くテクニック・ポイント〜3つのてんびん算・問題の内容を図や絵に描いて理解・「混ぜて半分」を描いて考える・てんびん算の意味・混ぜる食塩水と理科的視点・「混ぜて半分」の算数的意味・食塩水=食塩+水・問題 12解法〜」の話でした。
問題 12
「混ぜて半分」を描いて理解：図解してポイントを見つける
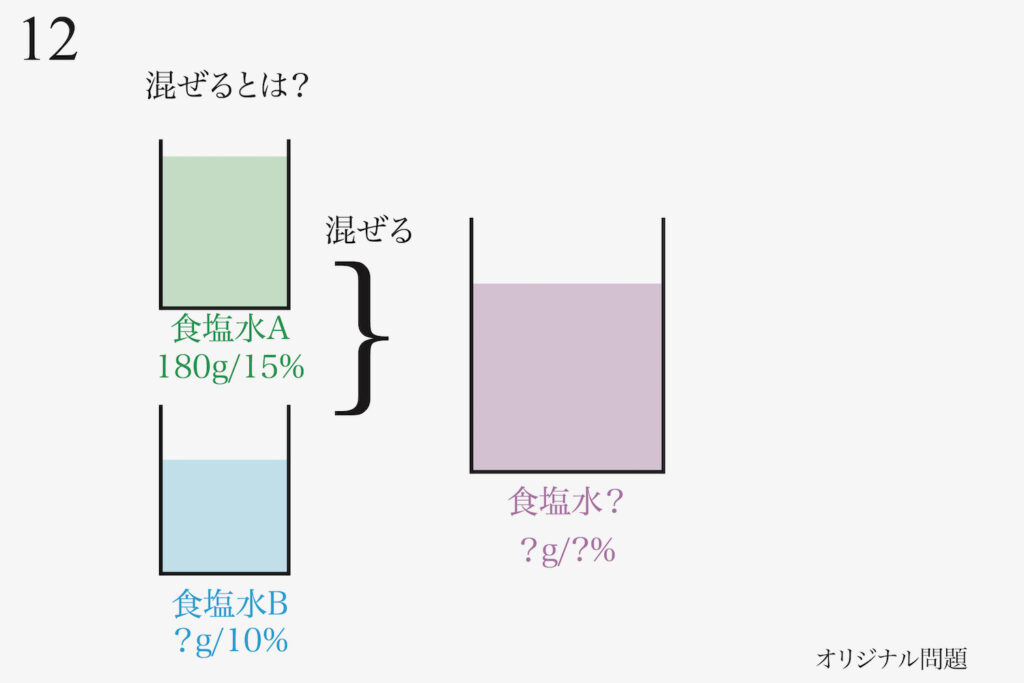
この問題が難しく感じられるのは、「文章が長く分かりにくい」ことと「食塩水を混ぜる」ことです。
・状況を簡単な絵や図に描く
・状況をしっかり理解することが解く第一歩
・大事な量・長さなどを見落とさない
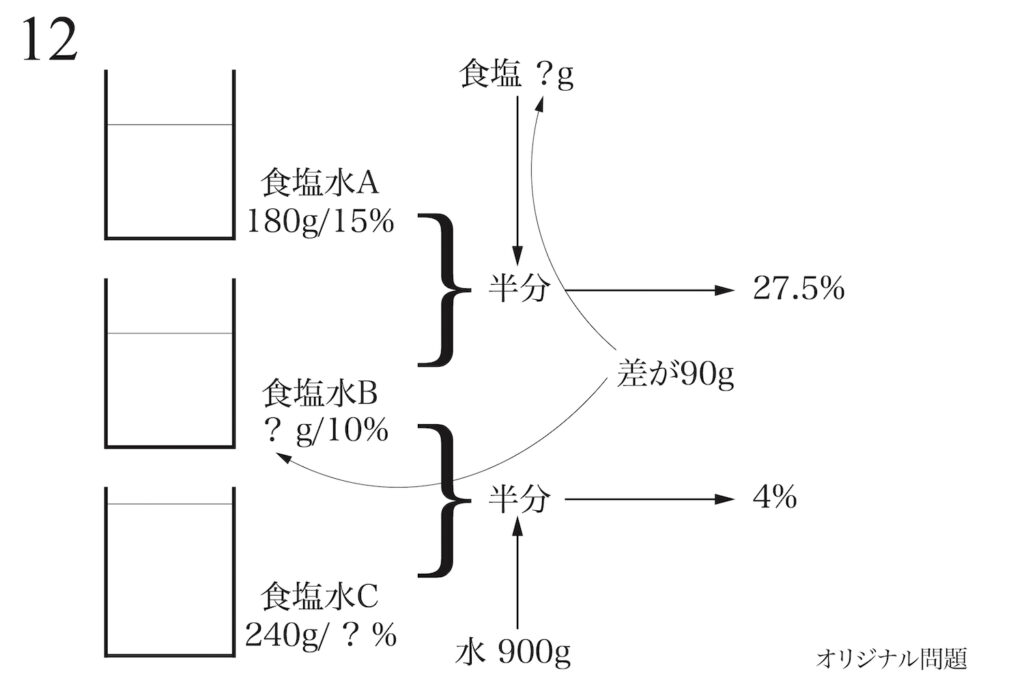
長い文章題では、自分で状況を描いて「きちんと理解する」ことが問題を解く第一歩です。
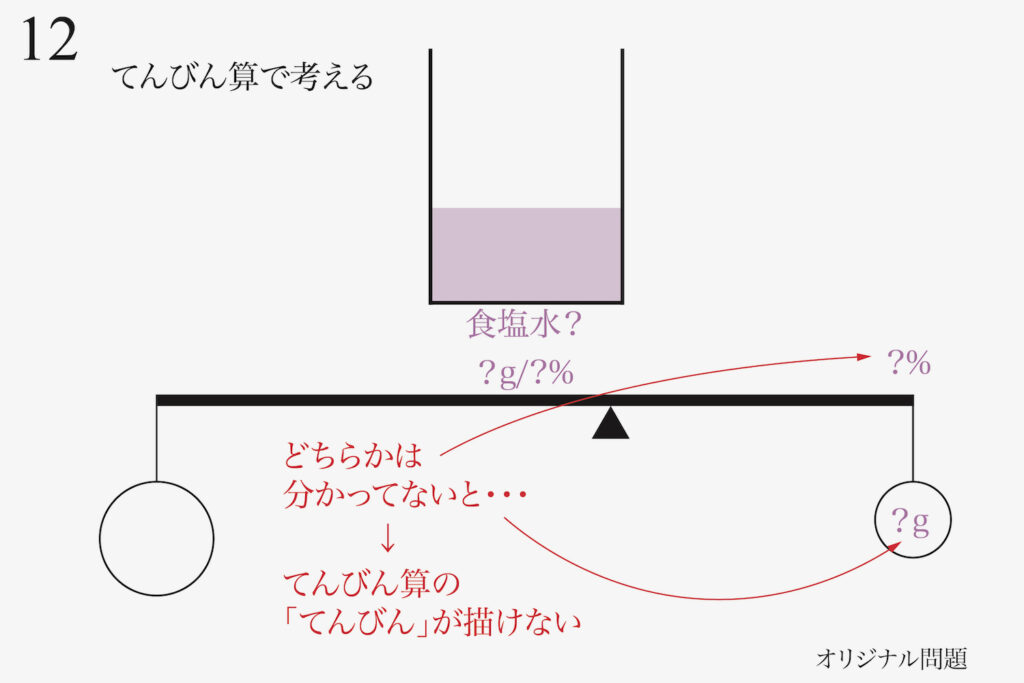
食塩水AとBを混ぜると「濃度も重さも不明な食塩水」が登場して、とても困ります。
ここで「手が止まってしまう」方が多いかもしれません。
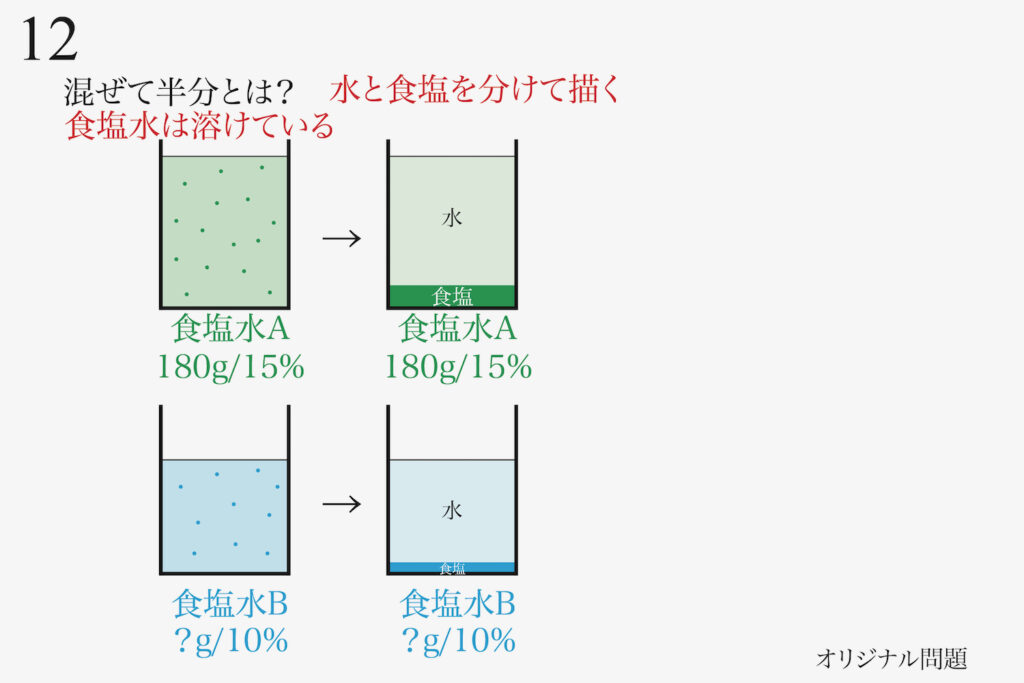
ここで、前回は「食塩水の状況を水と食塩を分離して描く」ことを考えました。
食塩水において「食塩は溶けている」のですが、元々は「食塩と水は別々のもの」です。
「溶けている」状況ですが、「食塩水=食塩+水」と考えたのです。
この問題は算数の問題ですが、この点は少し「理科的視点」かもしれません。
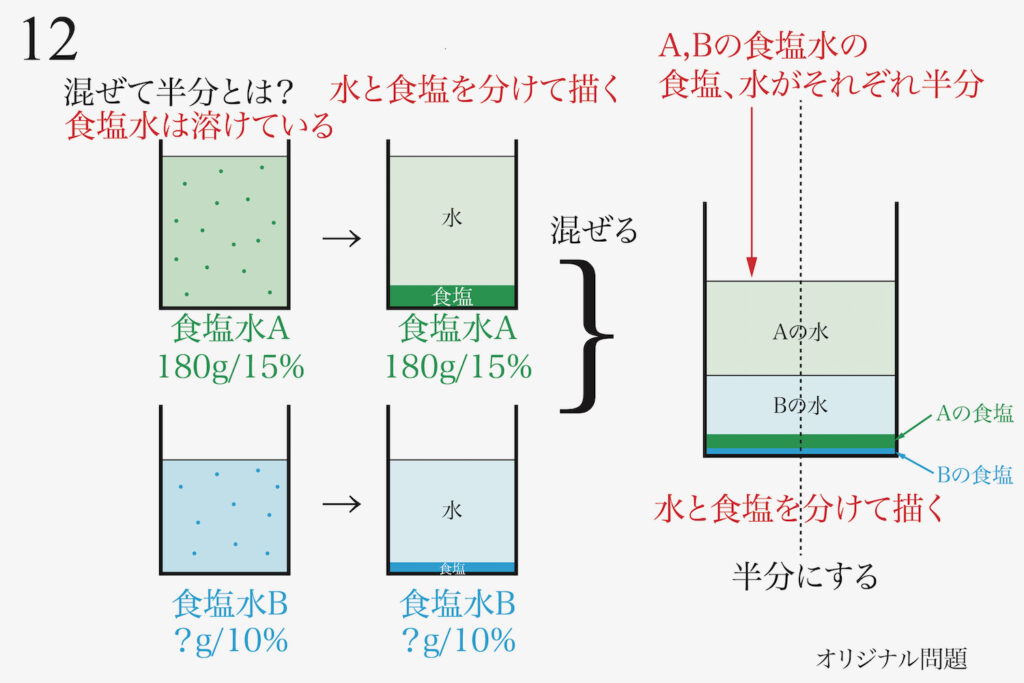
このように図解してみると、大事なことがわかりました。
「AとBを混ぜた食塩水」は「A,Bの食塩水の食塩、水がそれぞれ半分入っている」です。
・混ぜる前の食塩水を「それぞれ半分にして混ぜる」と同じ
・食塩と水が分離したイメージで描いて考える
男子小学生これが分かると
とても良いね！
女子小学生食塩水を「混ぜる」ことの
意味がよく分かった！
「混ぜて半分」にするので、「混ぜた食塩水」が分からなかったのが分かるようになりました。
「食塩と水を分離」して考えたことを復習しながら、改めて「混ぜて半分」を考えましょう。
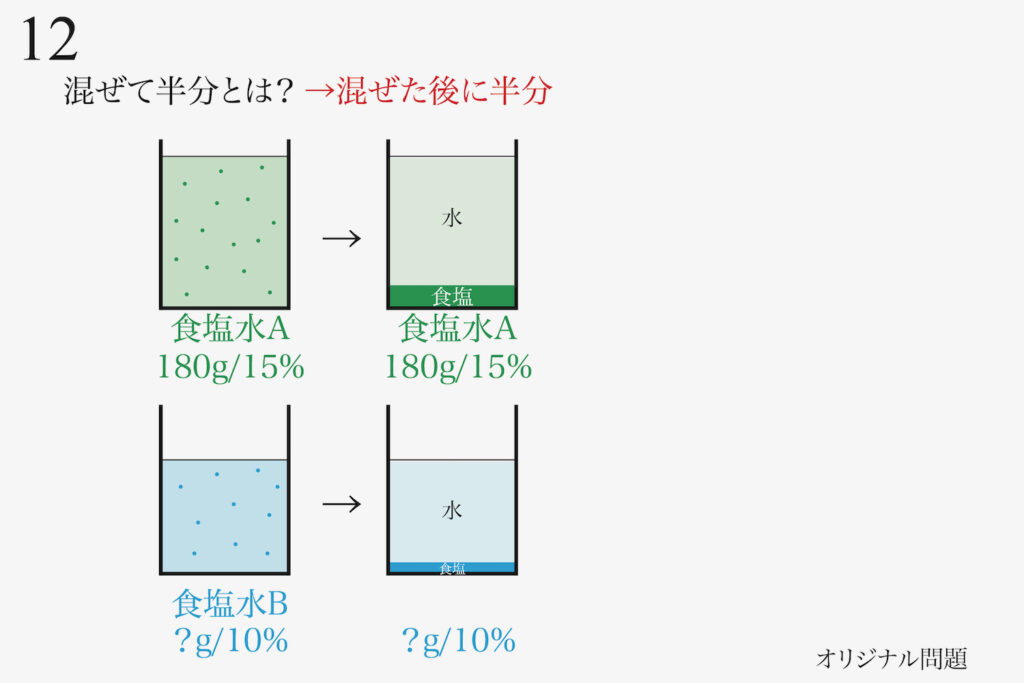
「混ぜて半分」とは「混ぜた後に半分」のことです。
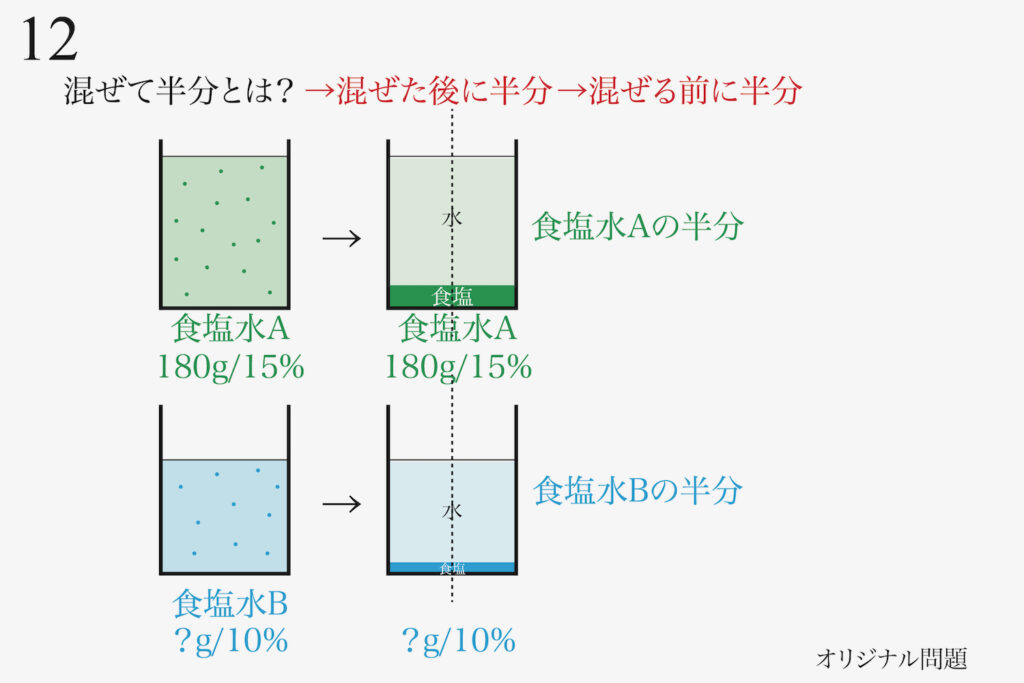
前回と同様に「混ぜた後」ではなく「混ぜる前に食塩水A,Bを半分」にしましょう。
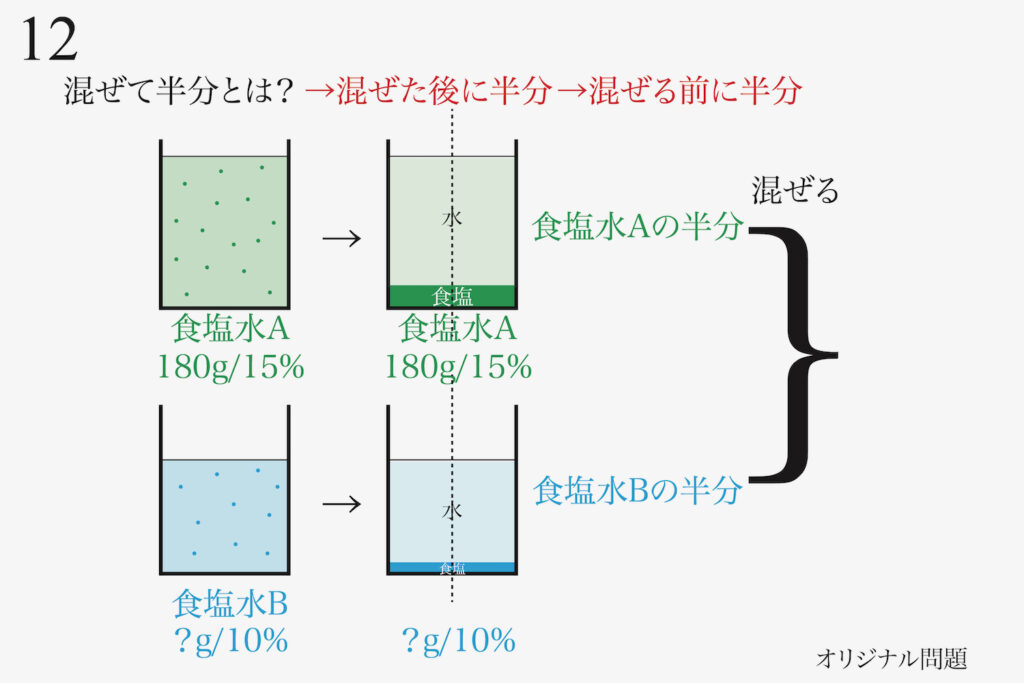
食塩水A,Bを「縦に割って半分」にして混ぜます。
実際に理科実験などでは、このように「スパッと縦に割る」は出来ませんが、イメージしてください。
男子小学生コップやビーカーは
割れないけど、絵なら割れるね！
女子小学生これは、模式図の
良いところだね！
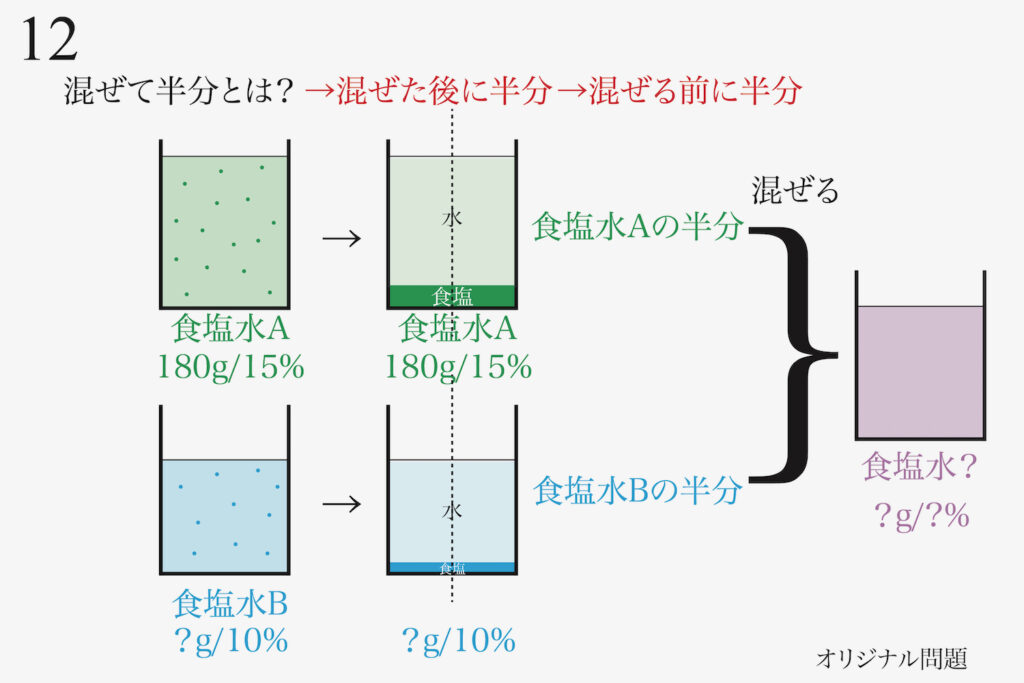
そして、「食塩水AとBの半分ずつ」を混ぜます。
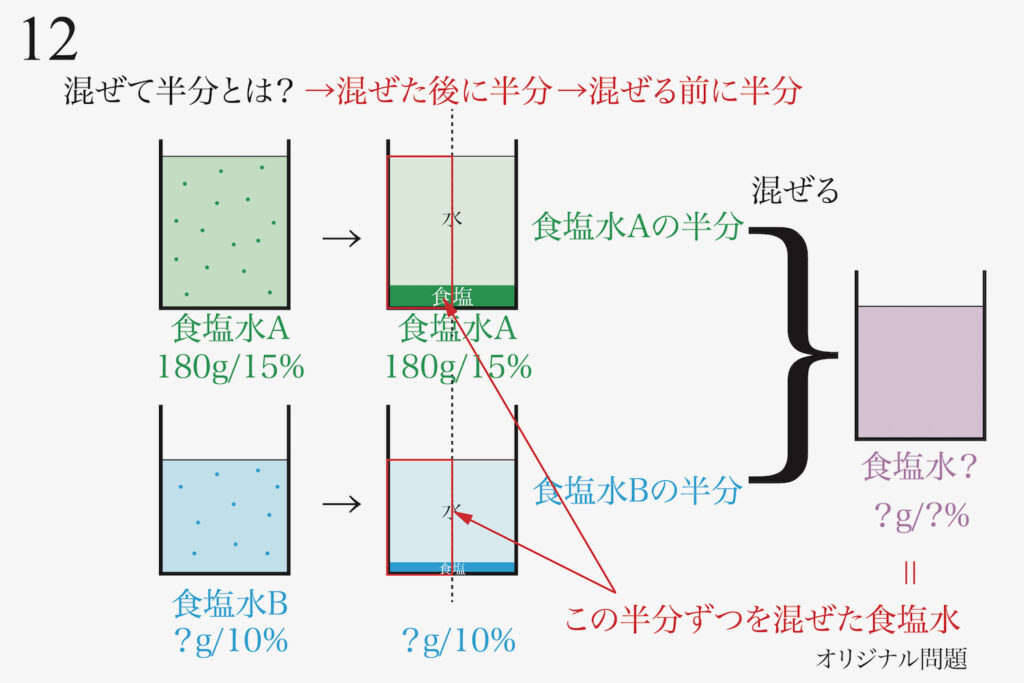
つまり、「混ぜて半分」の食塩水とは「食塩水AとBの半分ずつを混ぜた食塩水」が実態となります。
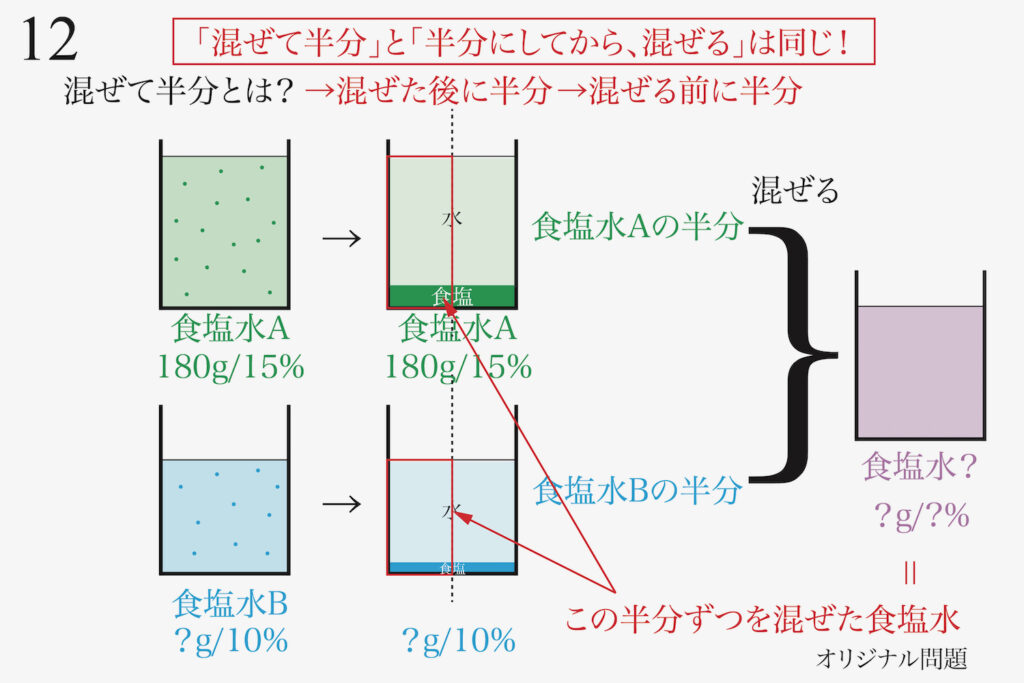
これで「混ぜて半分」は「半分にして混ぜる」と同じである、という大事なことが分かりました。
男子小学生これで、「混ぜて半分」の意味が
よく分かった！
女子小学生こう考えると、
とても面白い！
男子小学生この問題のように「混ぜる」時は、模式図を
描くと解けそう！
てんびん算の仕組みとポイント：「混ぜて半分」の食塩水
「混ぜて半分」の食塩水の実態がわかったので、その正体をてんびん算で考えてみましょう。
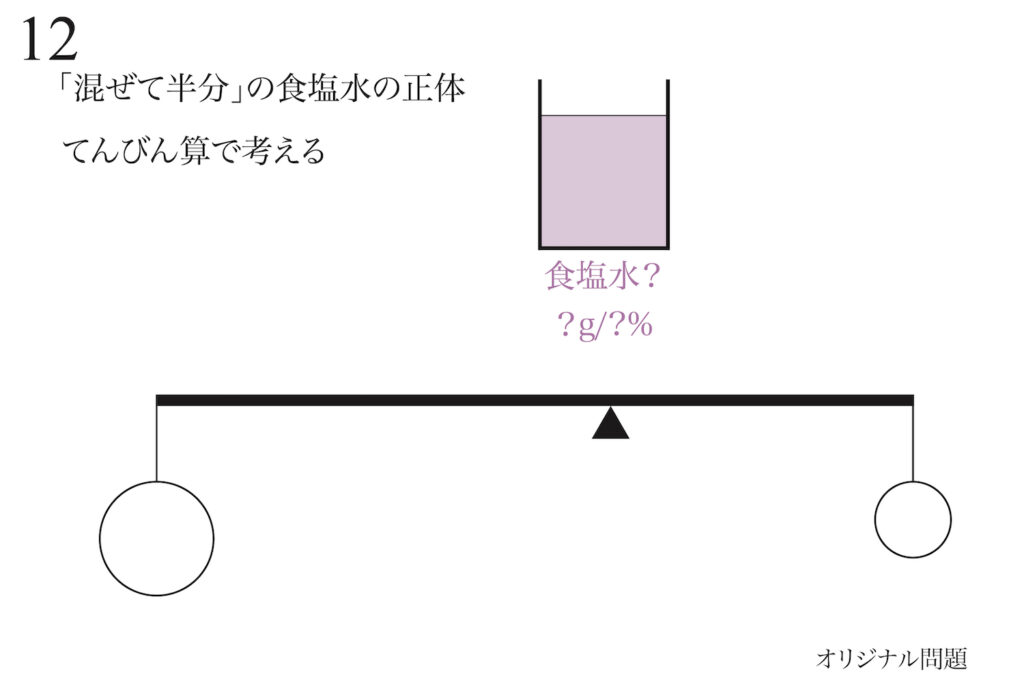
てんびん算で考えますが、「混ぜて半分」では分かりませんでした。
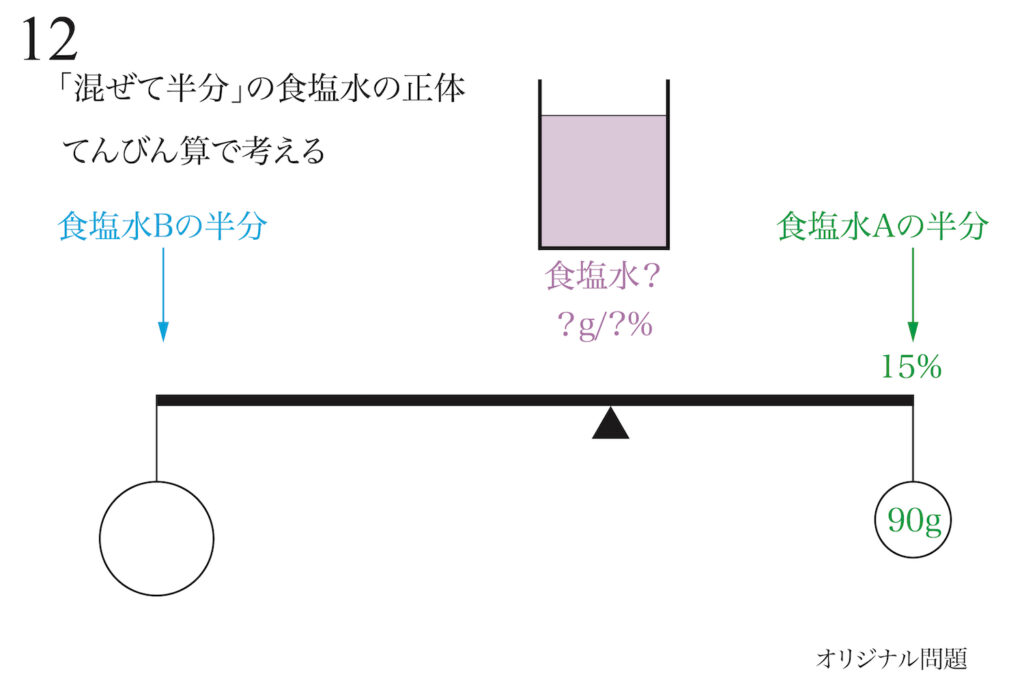
「半分にして混ぜる」と同じなので、「食塩水 A、Bの半分ずつを混ぜた食塩水」をてんびんで考えます。
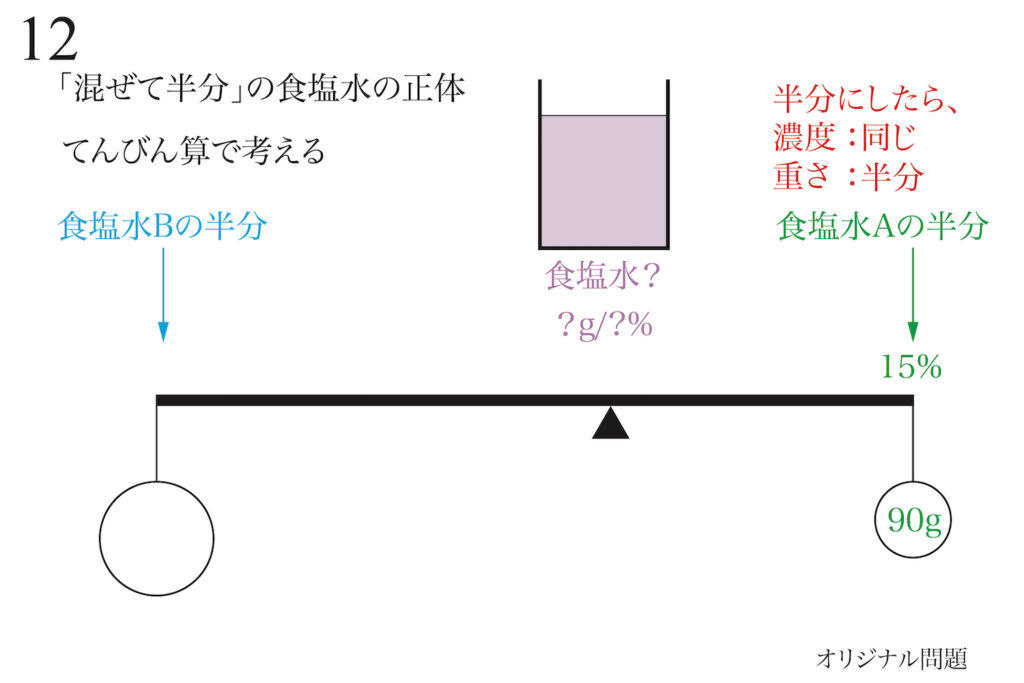
「食塩水を半分にする」ことは「濃度は同じで重さは半分」なので、食塩水Aの半分が分かります。
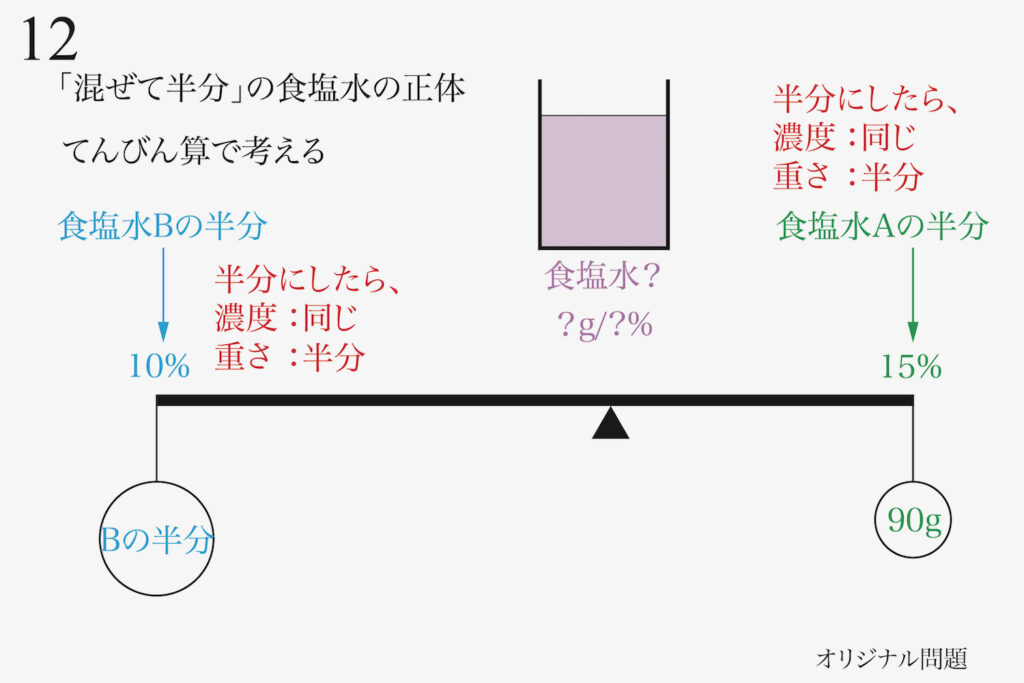
同じように「食塩水Bの半分」も、「濃度は同じで、重さは半分」です。
食塩水Bの重さが分かりませんので、ここでは「重さ=Bの半分」としておきましょう。
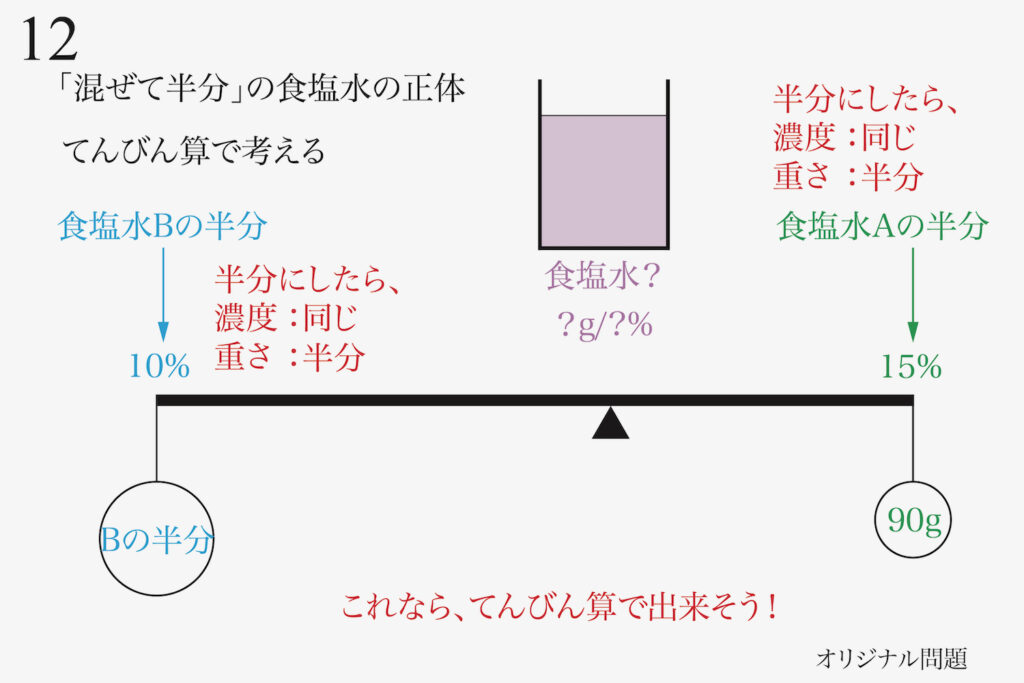
これなら、てんびん算で出来そうです。
ここまで表現できたら、
てんびん算で出来そう！
食塩と水の正体：食塩水と食塩と水の算数的視点
食塩水の問題では、「食塩水〜と食塩水〜を混ぜて・・・」という問題が多いです。
今回の問題は、食塩水ではなく「食塩と水を混ぜる」です。
改めて、食塩とは何か、水とは何かを考えてみましょう。
食塩とは「濃度100%の食塩水」で、水とは「濃度0%の食塩水」です。
男子小学生えっ？
そうなの？
女子小学生食塩・水だけだと、
食塩水ではないと思うけど・・・
理科的には「食塩水ではない」かもしれないので、それぞれ（）書きにしてみましょう。
算数的に考えてみると、食塩水の濃度は0〜100%です。
食塩水は、「水（0%）→食塩水(0〜100%）→食塩(100%」と連続的に変化すると考えられます。
男子小学生まあ、
そうかも・・・
女子小学生ちょっと、
しっくりこないかな・・・
あまり難しく考えず、食塩水は「食塩と水の状態変化」と考えてみましょう。
水は温度で「固体（0）→液体（0〜100℃）→気体（100℃）」と連続的に変化します。
男子小学生うん。
それは理科で習ったよ。
水がこのように変化するのと同じように、「食塩も変化する」と考えてみましょう。
女子小学生そう考えると、
食塩と水も、てんびん算で出来そう。
「食塩=濃度100%の食塩水」で「水=濃度0%の食塩水」と考えてみましょう。
・食塩水の濃度は0%から100%まで連続的に変化する
・塩は「濃度100%の食塩水」で、（真）水は「濃度0%の食塩水」
すると、てんびん算で考えることが出来ます。
この考え方は、「理科的ではない」と考えるかもしれませんが、実は「とても理科的」な考え方です。
モノや状態は、水や液体のように連続的に（緩やかに）変化してゆくと考えることが本質的です。
次回は、これら考えたことをもとに問題を解いてゆきましょう。
次回は下記リンクです。
