前回は「複雑な図形問題が「分からない」から「分かる」へ〜正三角形・図形的センスと補助線のコツ・求めたい比と平行から相似形を探す・つくる・正三角形IDCの大きさの大体の予想・図形の勘を磨く・問題10(2)解法〜」の話でした。
問題 10（再掲載）
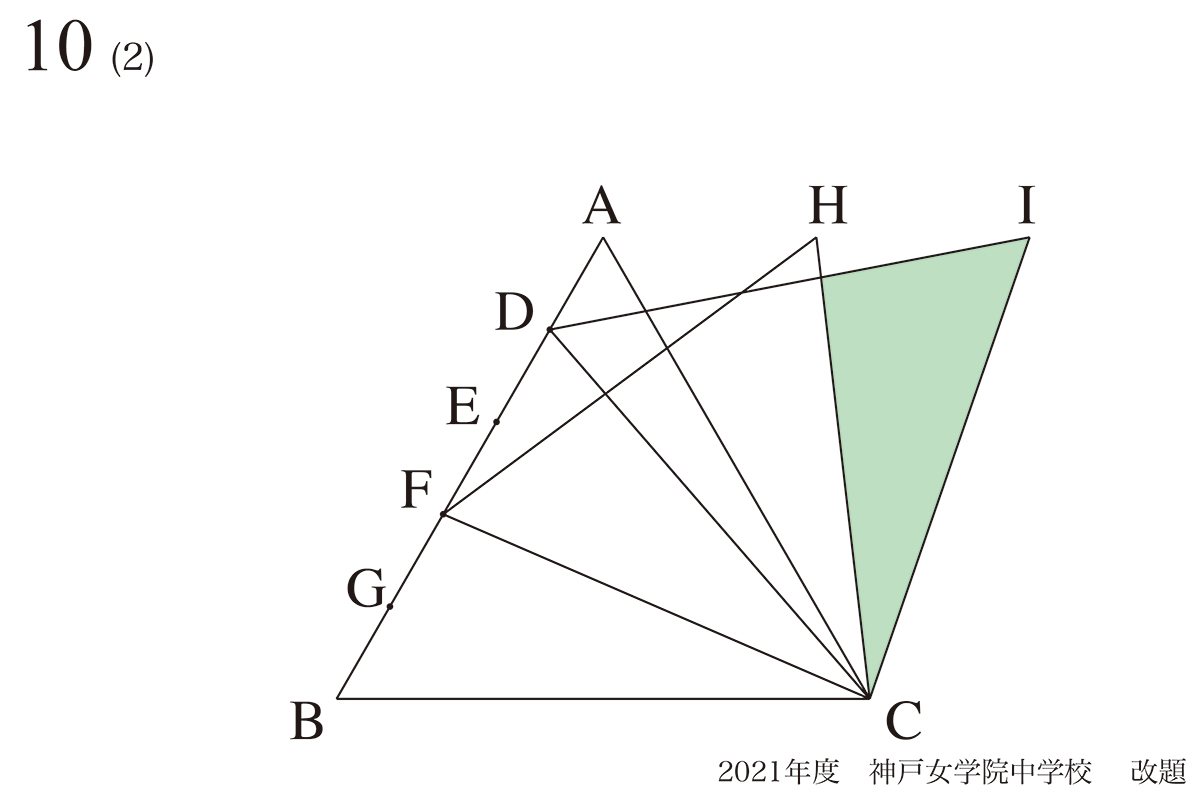
図形の性質を考える：正三角形はどのように出来てゆくか
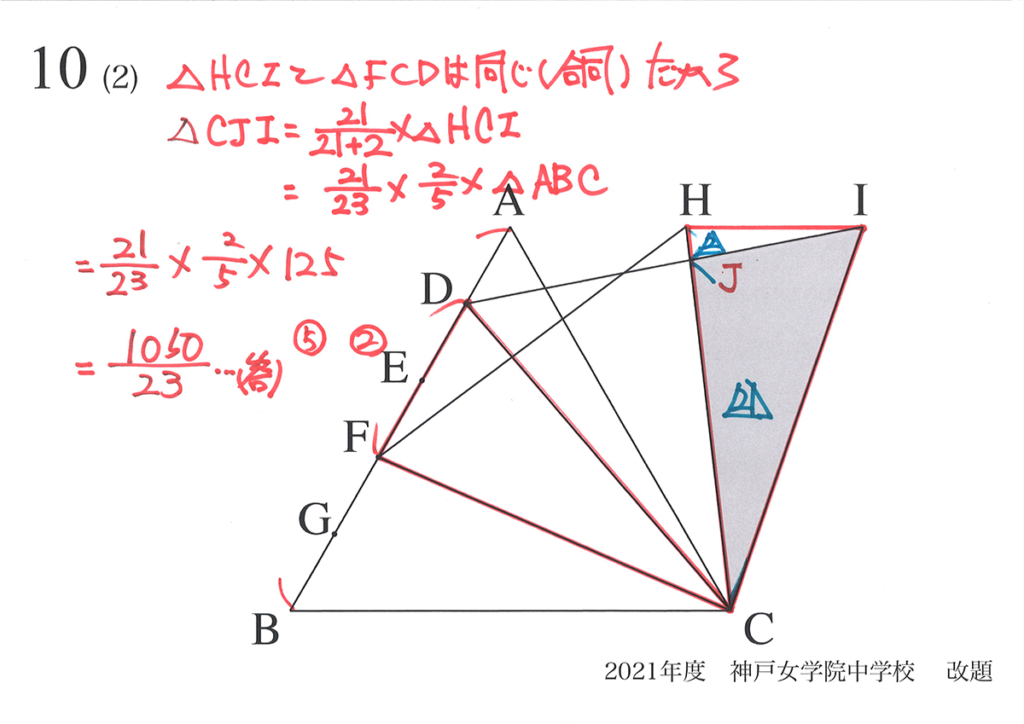
(2)の面積を求めることが出来ました。
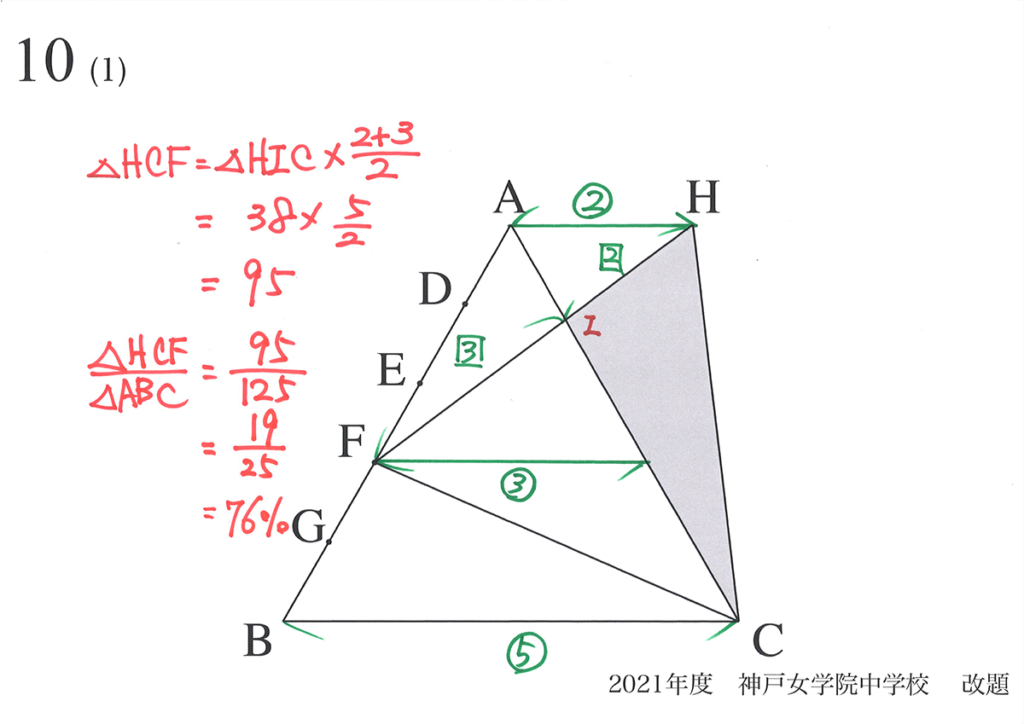
(1)と同様に「寄り道」して、正三角形IDCの面積を求めて「正三角形ABCと比較」してみましょう。
計算する前に、ちょっと予想してみましょう。
図を描いてみて、正三角形FCHと正三角形DCIはどちらが大きそうでしょうか？
男子小学生正三角形IDCの大きさって、
正三角形HFCの大きさに似ているね・・・
女子小学生ちょっと
違いそうな気がする・・・
男子小学生ちょっとした違いだけど、
なんとなく正三角形DCIの方が大きそうな気がする・・・
「なんとなく」という感覚でも良いので、少しずつ考えると図形の感が磨かれるでしょう。
男子小学生正三角形IDCと正三角形HFCって、
同じ正三角形だから、相似だね。
男子小学生だから、面積は
辺の長さの比と一緒に大きくなるね。
女子小学生そうね。
だから、HFとIDの長さを比較すればいいのかな？
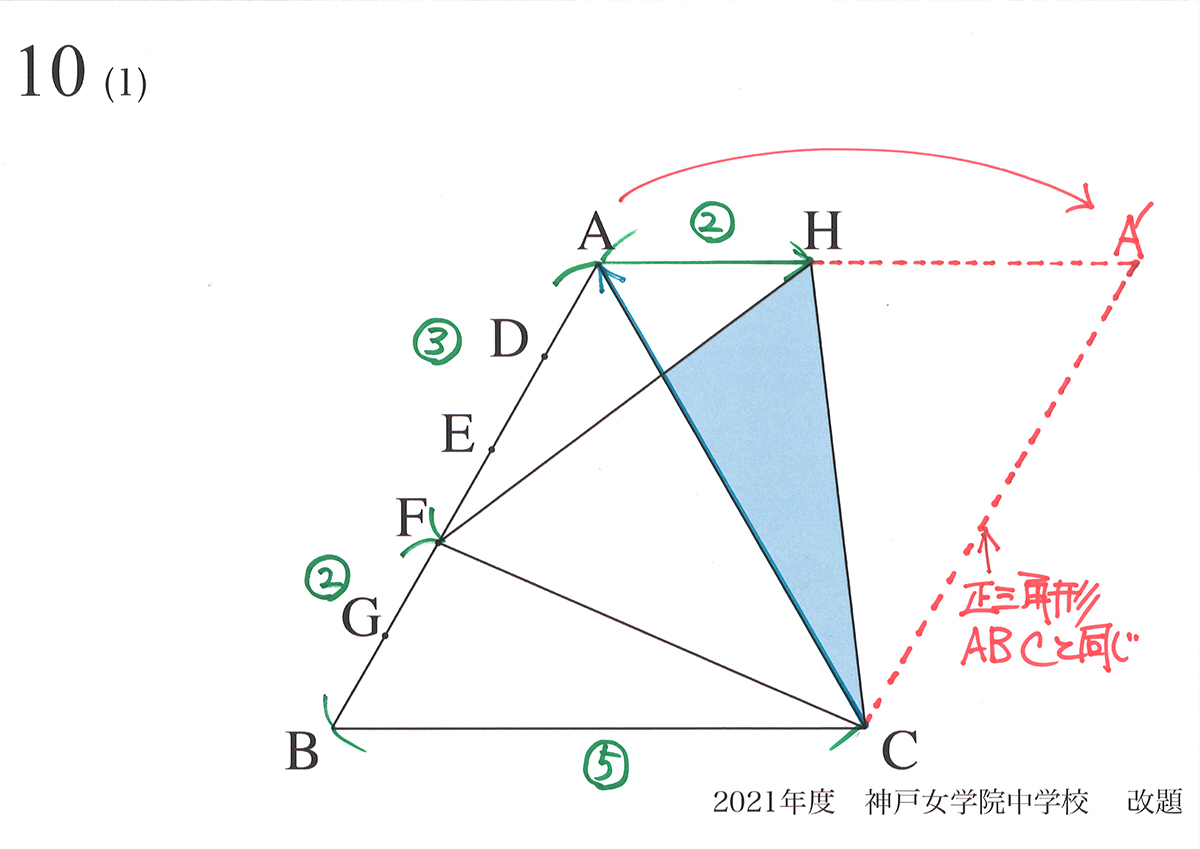
「矢印の話」で考えるとFもDもBから出発して、それにともなって上図のAA’をA→H→Iと移動します。
その過程で、出発点B=Fと考えると正三角形ABCから正三角形HFCとなり、面積が減少しました。
Fは、出発地点Bから2/5の位置、Dは4/5の位置で、B→F→D→Aと移動してゆきます。
最後にできる正三角形はA’ACとなり、元の面積に戻ります。
男子小学生あっそうか！
最初から最後で同じ正三角形になるね！
女子小学生その途中で、正三角形HFCは
かなり小さくなって「正三角形ABCの76%」だから・・・
男子小学生なんか、正三角形IDCの方が、
正三角形HFCより大きい気がする・・・
ここで、「正三角形IDCの面積>正三角形HFCの面積」と推測できます。
何が分かれば面積が求まるか：辺の長さを分割して計算
それでは、求めた面積を緑色の部分の面積を使って、正三角形IDCの面積を計算しましょう。
この正三角形IDC面積を知るには、「どこの比が分かれば良いか」考えましょう。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
男子小学生ええっと・・・
(2)の三角形と正三角形IDCの面積と辺の比を考えて・・・
DJ : JIが分かれば良さそうです。
では相似形を見つけて、求めてみましょう。
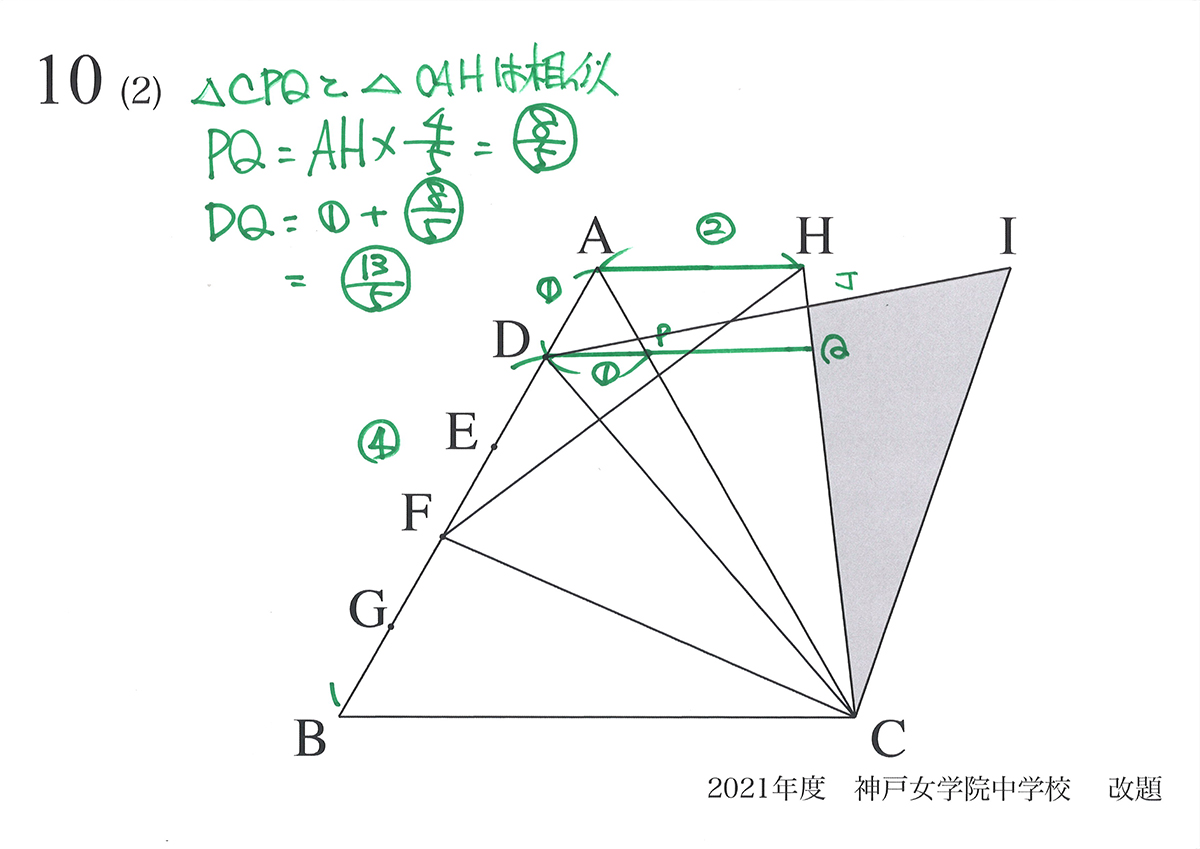
上手では、DJ : JIを求めるために、DQの長さを求めています。
ここではDQが一気に分からないので、DQ=DP + PQと分割して計算しています。
このように、辺の長さや面積が「一気に分からない」時は「分割する」と良いでしょう。
・平行な線、相似形を探す・つくる
・相似比となる「対応する辺」の長さを計算
・「対応する辺の長さ」が分かりにくい時は、辺を分割して考える
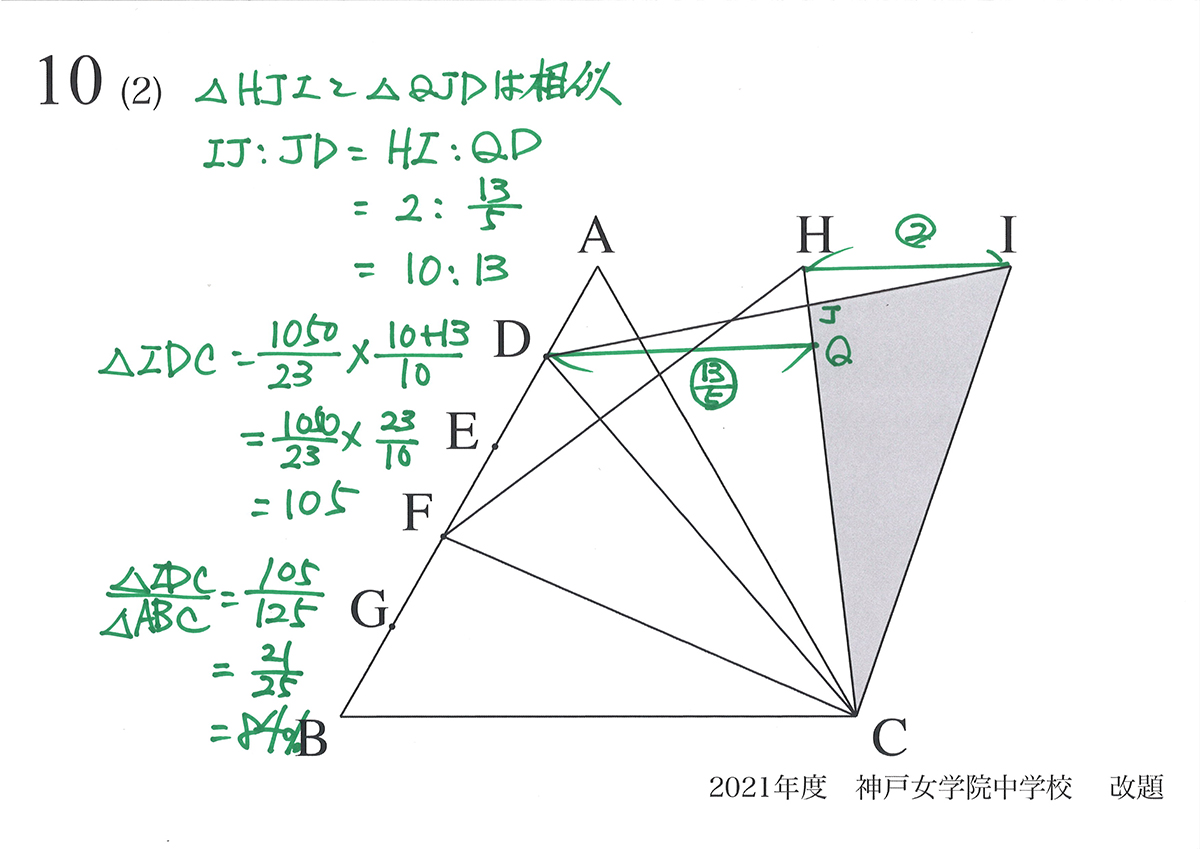
これで、DJ : JIの比が分かったので、正三角形DICの面積が求まります。
計算してみると、「正三角形DIC=正三角形ABCの84%」でした。
女子小学生さっきの「正三角形HFC=正三角形ABCの76%」から
ちょっと増えたね！
「正三角形FCH=正三角形ABCの76%」だったので、8%大きくなりました。
男子小学生ということは、約10%大きくなったから、
正三角形ABCの1/10くらい大きくなったんだ・・・
「面積は正三角形ABCの何％か求めよ」という問題の場合、上のようにしっかり計算することが大事です。
計算して「8%上昇」に対して、
女子小学生大体10%くらい
大きくなったんだ・・・
このように「大体の変化を把握する」と良いでしょう。
「大体〜くらい」という感覚を持つことは、算数・理科では大事な姿勢です。
次回は下記リンクです。
