前回は「直角二等辺三角形の斜辺・対角線の長さの公式を理解〜図形の外に直角二等辺三角形を展開・直角二等辺三角形の特徴と性質・直角二等辺三角形の「斜辺しか分からない」とき・正方形をつくる・問題 11(3)解法B〜」の話でした。
問題11(4)(再掲載)
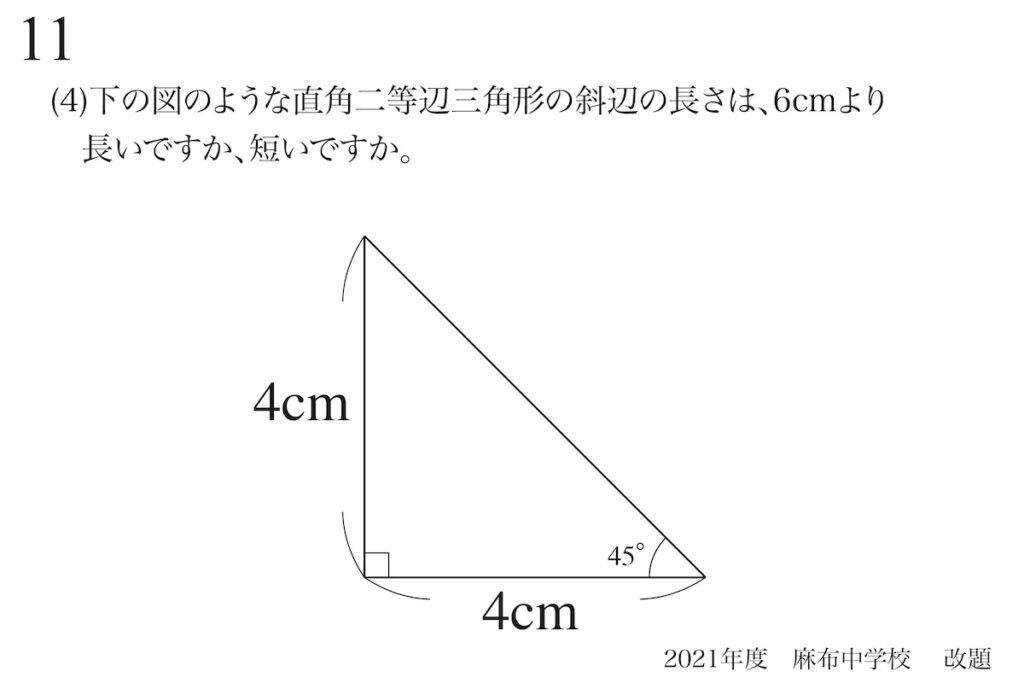
問題のヒントを探す:直角二等辺三角形の斜辺の長さの比較
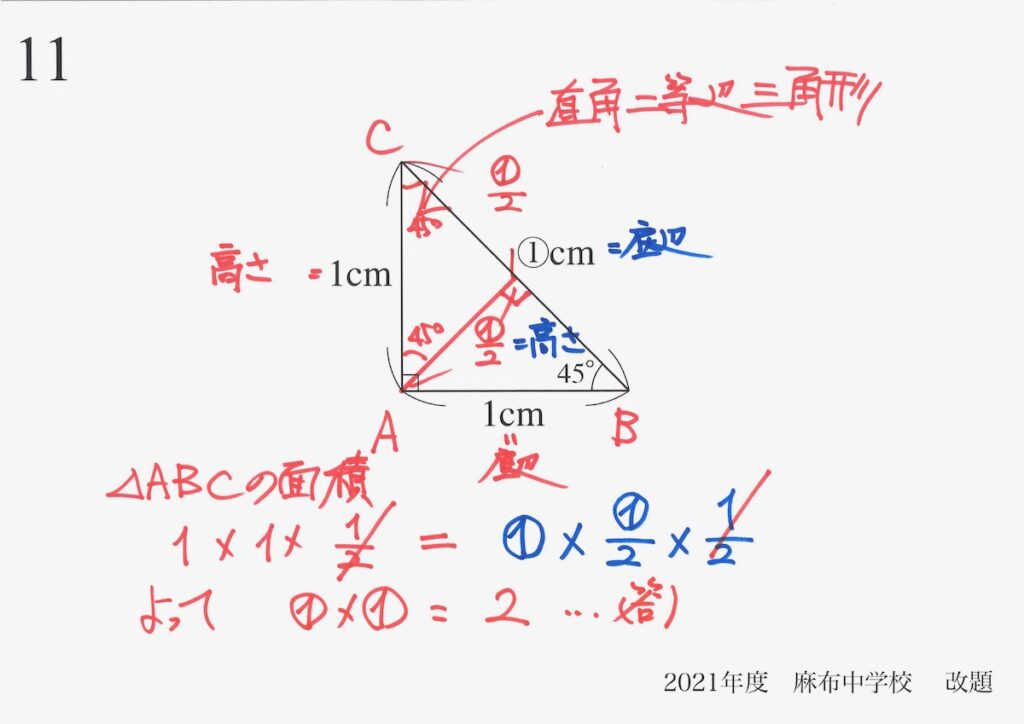
具体的な長さが算数では分からない「直角二等辺三角形の斜辺・対角線の長さ」を考えました。
・直角を挟む辺の長さが同じ三角形
・直角以外の角度は45度(直角の半分)の三角形
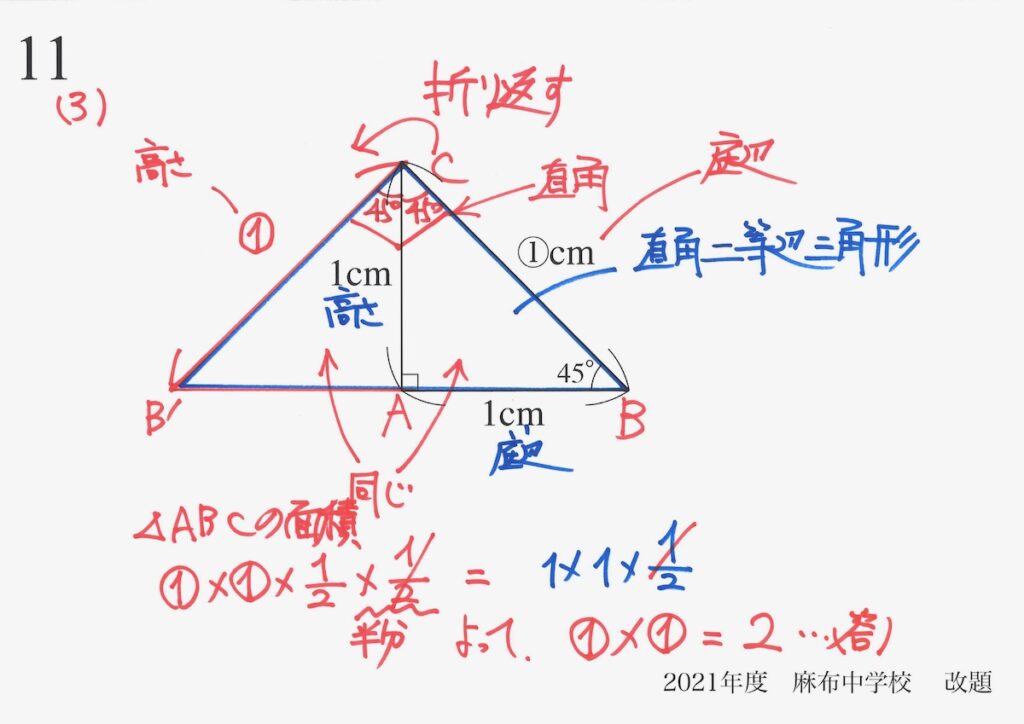
直角二等辺三角形形の中で折り返したり、図形の外に折り返して、面積を比較しました。
・図形の形を三角形・四角形に分割
・底辺と斜辺の見方を変えて、面積を計算
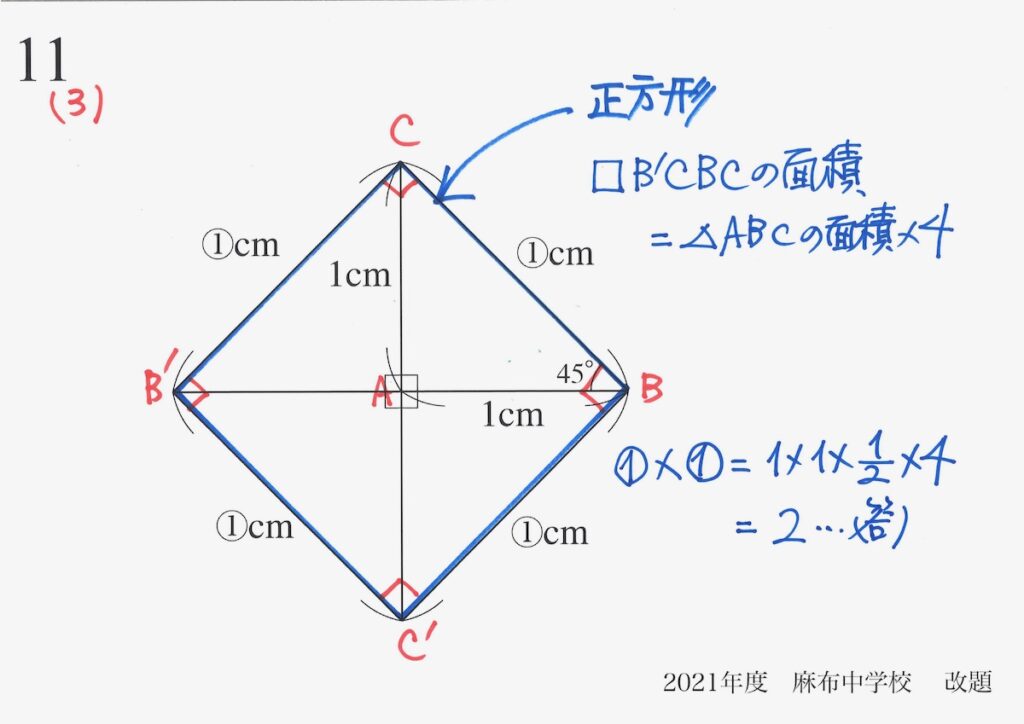
最後にもう一度折り返すと、二等辺三角形から正方形が出来ました。
斜辺の長さは具体的には分かりませんが、「斜辺x斜辺」は分かりました。
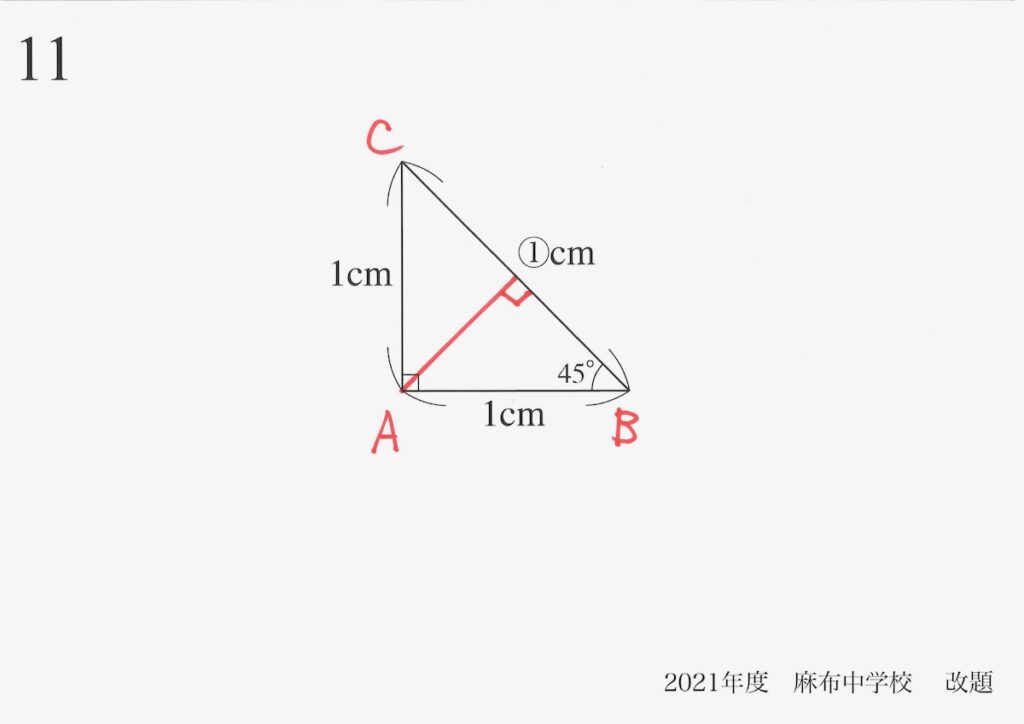
これまでは「一辺の長さ=1」の直角二等辺三角形でしたが、今回は「一辺の長さ=4」の直角二等辺三角形です。
 男子小学生
男子小学生似ているっていうか、
両方とも相似形だね・・・



同じように
考えれば出来そうだけど・・・



でも、今回は「長さの比較」だから、
ちょっと違うね・・・
大問の中で、小問がいくつかある場合は、「それぞれがヒントになっている」可能性があります。
出題者が「最も問いたい」のは、最後の小問であることが多いです。
いくつかの小問に別れている理由は、
1.最後の問題のみだと難しいため、ヒントを作って解きやすくする
2.問題を分け、出来る部分を明確にして、採点の際に点数の差が出やすくする
などの理由があります。
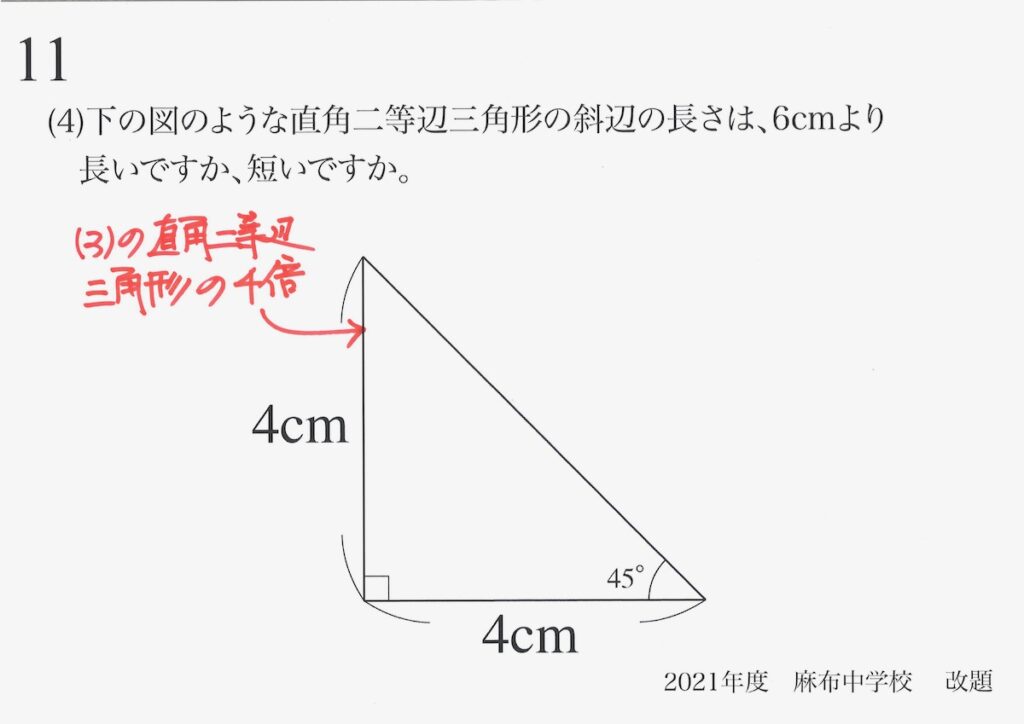

(4)の図形は(3)の図形の4倍の図形(相似形)です。
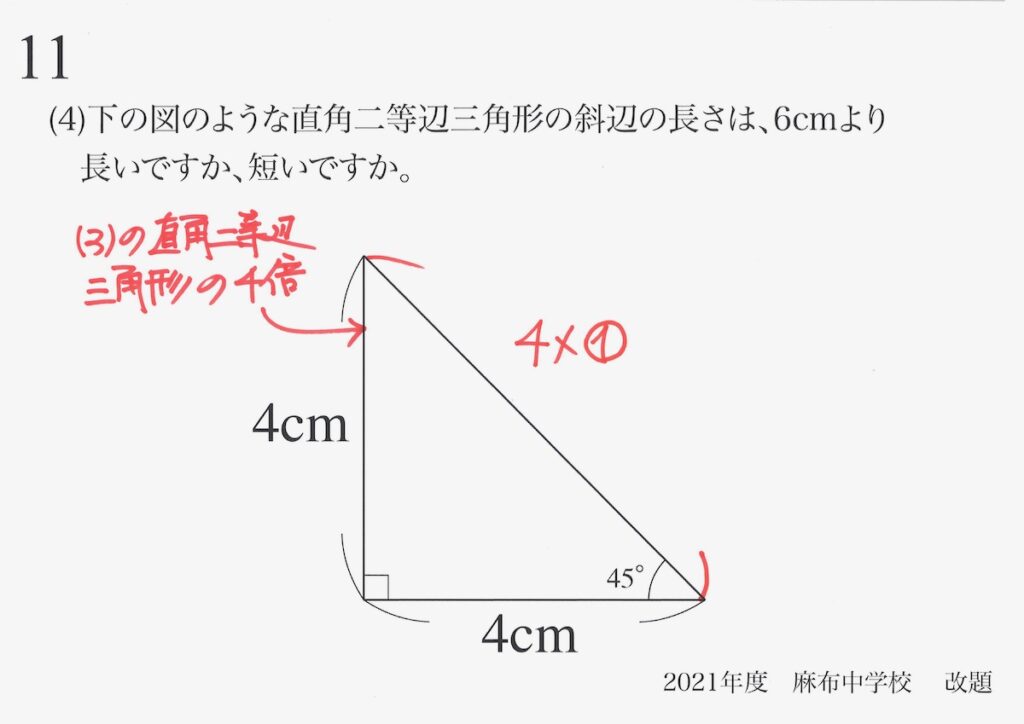

斜辺の長さは、(3)で求めた結果が使えそうです。



斜辺の長さは、
4倍の4x①=④になるね!
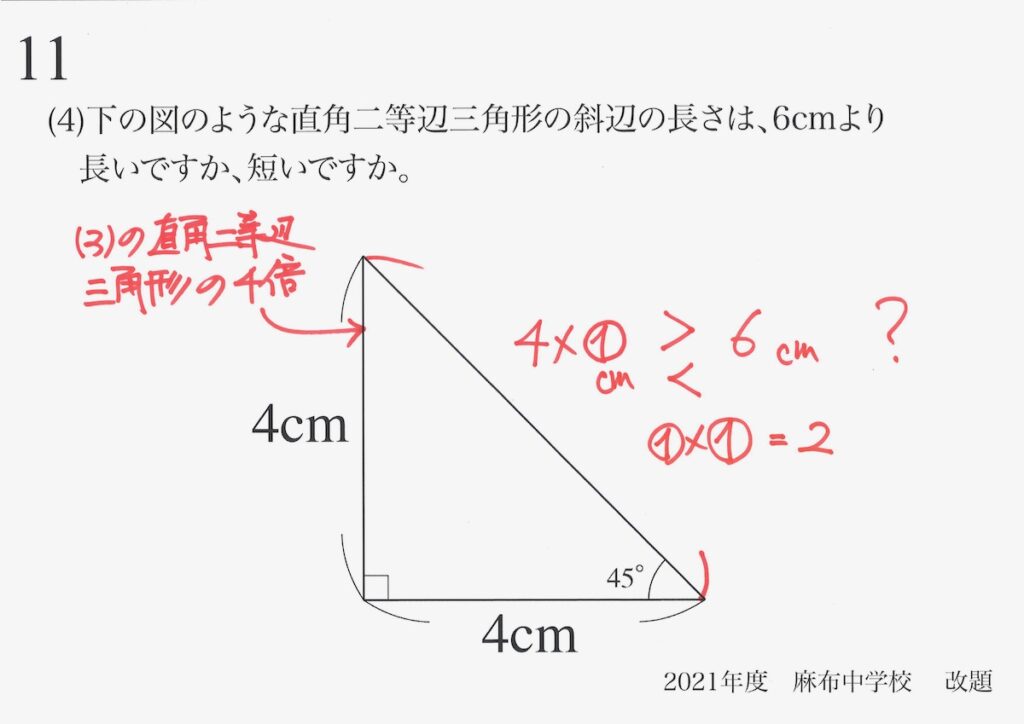

この長さが「6cmより大きいか、小さいか」を、考えてみましょう。
(3)の結果を使って
長さは分かったから、あとはどう考えようかな・・・
「2回掛けた数字・自乗」を比較


「具体的な長さ・面積など数字を求めること」と、「長さ・大きさ等を比較すること」は大きく異なります。
今回は、「長さを比較」します。
斜辺の長さにある①は、「2回かけた数」は分かりますが、「1回だけかけた数」が不明です。
「2回掛ける」のは「自乗」または「2乗」と呼び、中学以降の数学の内容です。
中学受験で一部「累乗」の問題が見受けられますが、「2回掛けた長さ(量)」を比較しましょう。



2回掛けると
分からないよ・・・


そこで、「2回かける」ように考えましょう。


「2回かける」と「掛け算の大事な性質」を考えましょう。



掛け算は、掛ける順番を
変えてもいいね!


「かける順序が変えても同じ」です。



あっ!
ここで、(3)の結果が使えそうだね!


後半の「①x①」は(3)から分かっているので、計算できます。



ここからは、
計算できる!





これで分かったけど、
片方だけ「2回掛けて」比較していいの?



片方だけ「2回掛けて」比較は、
不釣り合いになると思うけど・・・
比較する一方を「2回かけた」ので、もう一方も2回かけましょう。



あっそうか!
同じ条件にすればいいんだ!


これで、大きさが比較出来そうです。


「2回かけた数」の大小が分かりました。


「長さを2回掛けた量」と長さの大小は同じなので、比較ができました。



少し不思議な
感じがするけど・・・



「分からない数字」が
比較できるって、面白い!
次回は(5)の解法のご紹介で、下記リンクです。


