前回は「算数の学力アップ学習法〜「できない」から「できる」へ・状況を把握して試行錯誤・考え方を習得・しっかり理解する大事さ〜」の話でした。
中学受験算数と一次方程式
今回は、「算数と方程式の話」です。
中学受験の算数を学ぶ際に「方程式を学んだ方が良いか、どうか」という話があります。
男子小学生方程式って
難しそうだけど・・・
女子小学生方程式は中学生でなければ、
できないんじゃないの？
小学生にとって、方程式=「ほうていしき」という言葉・音自体が難しい印象があります。
方程式といっても、一次方程式と二次方程式では難易度が大きく異なります。
また、未知数の数によって難易度はだいぶ変わります。
まずは、一次方程式の話にしましょう。
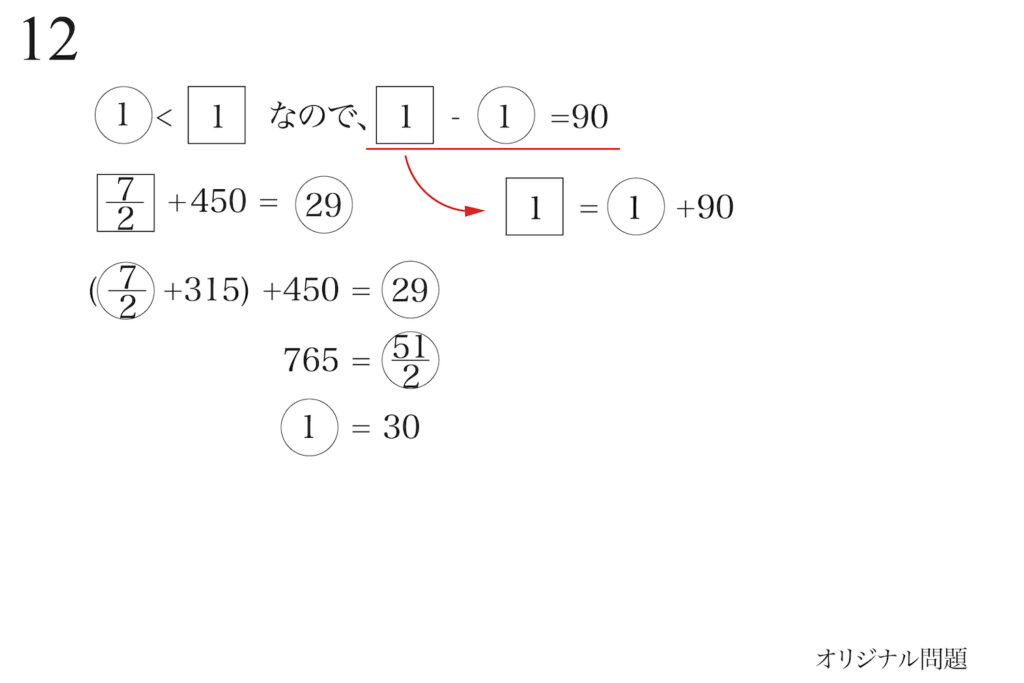
実は、中学入試算数においては「一次方程式が普通に使われている」のが実態です。
上の式において、①などと未知数を置く解き方です。
「未知数をX」としても全く同じ考え方です。
ただ、「X（エックス）」と言われると小学生は、
男子小学生Xって
なんだか難しそう・・・
とても難しく感じてしまいます。
そこで、「未知数を①」として、
塾講師ここでは分からないことを、
「丸の1」と置きましょう！
未知数をXではなく①として、立式して解くのです。
場合によっては、2つか3つの未知数を、
塾講師これも分からないから、
「三角の1」と置きましょう！
「三角の1」や「四角の1」と置いて、「方程式として解いている」のが現実です。
女子小学生これは
方程式とは思っていなかったけど・・・
女子小学生実は
方程式だったんだね！
受験生たちは「方程式とは考えずに」設置して解いていることもあります。
「方程式で解く」とは考えない姿勢
「方程式とは言わずに、代数的考え方で解く」のは良いことかもしれません。
「分からないこと」を仮に設定して考える思考は、
塾講師分からないことを
□と置いて考えましょう・・・
小学校中学年の教科書にも記載されているので、「未知数設定」は標準として良いと思います。
子どもにとって①などは、
男子小学生分からない数を
①とか置いているだけだから・・・
「ケーキの数」とかと同じように考えられますから、それほど負担に感じないと思います。
一方で、「方程式で解く」思考に関して、
受験生の父親それは
方程式で簡単に解けるね！
まだ小学生である中学受験生に対して「方程式で出来る」と子どもに伝えるのは、お勧めしません。
非常に算数の学力が高く、算数がとても好きで得意な受験生は別かもしれません。
男子小学生僕は算数がすごく好きで、
得意だから、方程式でも出来るよ！
「数学的発想にまで踏み込んでいる一部の例外的な方」は「方程式で良い」と考えます。
そういう「ごく少数の方」は別として、一般的には「方程式で」とは考えない方が良いでしょう。
方程式ではなく大事な「小学生らしい」柔軟な思考
分からないこと・ものを「未知数」として設定する方程式は、とても便利な側面があります。
中学生になって算数が数学になると、まず代数学を学びます。
ここで、
中学教員A未知数をX,Yを置いて、
立式してみましょう・・・
このように方程式の基礎を教わって、「数学の入口に入る」ことになります。
とにかく「分からないことを未知数」として「条件に合わせて立式」することは、代数学の基本です。
中学生以降になると、この「未知数と立式」の思考が非常に大事になります。
一方で、「小学生は小学生らしい柔軟な思考」が大事です。
「未知数と立式」の思考は、ある意味では「機械的発想」でもあります。
そして、この「機械的発想」は「あまり考えないでも出来る」考え方です。
この「考えないでも出来る」考え方というのは、語弊があるかもしれませんが、現実です。
とにかく、
塾講師分からないものは
全部未知数で設定！
塾講師これはx、これはy、これはzにして、
立式して・・・
多くの問題で、未知数設定して、ガリガリ計算すればできます。
この「ガリガリ計算する」も学力が必要ですが、根幹は比較的易しいです。
「未知数の置き方」にもコツがありますが、とにかく「未知数を置いて立式する」だけが代数の基本です。
算数は結構奥深くて、ある程度数学ができる人でも解けない問題が多数あります。
小学生の頃から、この「ある種機械的な発想」を身につけると、のちに伸びなくなる可能性があります。
「算数的思考の奥深さ」を学ばずに、「中学以降の数学的発想」にジャンプすることは危険でもあります。
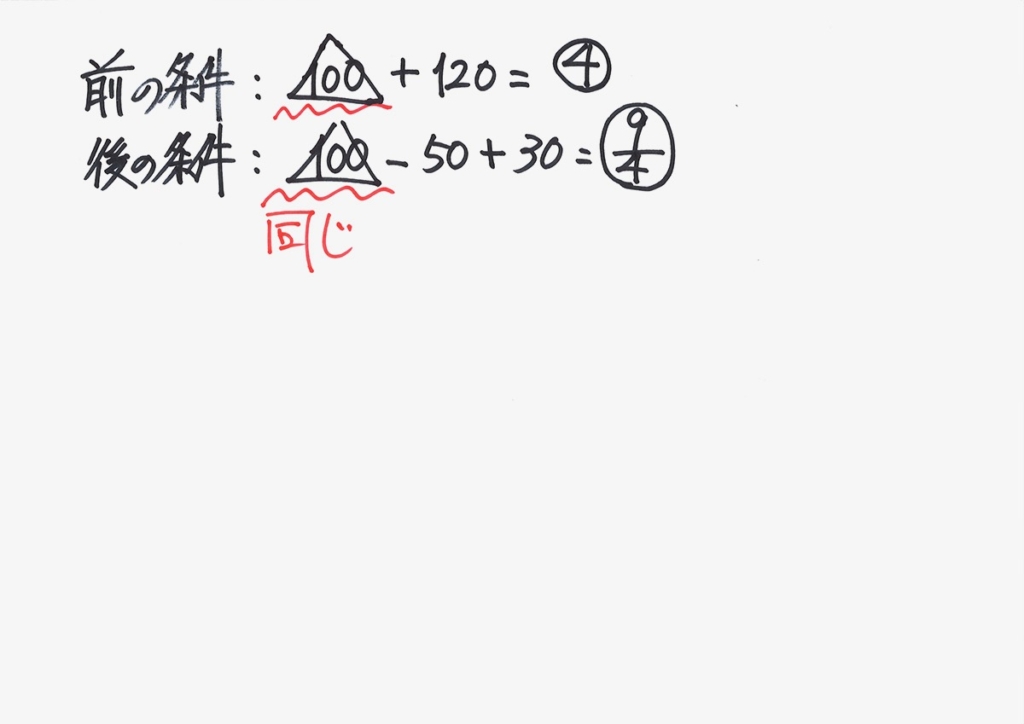
「おもりを入れ替える」問題で、未知数を設定して立式して解く考え方をご紹介しました。（上記リンク）
これは、オーソドックスな考え方で、難関校〜を目指す中学受験生には身につけて欲しい発想です。
こういう問題を考えるとき、「対象が2つ」だと簡単ですが「対象が3つ（以上）」になると、
男子小学生考える対象が
多すぎて・・・
一気に難しくなる傾向があります。
これは、理科の電気の問題で「電圧・抵抗・電流の3つ」が登場するので難しいのと同じです。
電気の問題のわかりやすい考え方を、上記リンクでご紹介しています。
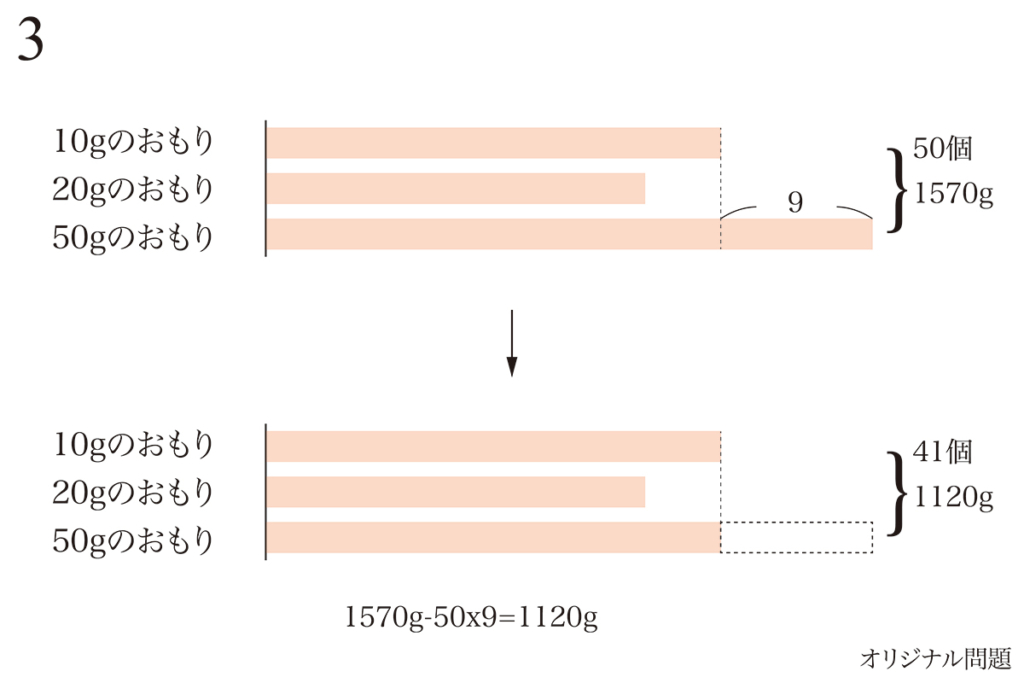
「対象が3つ」の時は、
女子小学生対象を
2つにできないかな・・・
「対象を2つに減らす」ことを考えてみましょう。
すると、上の棒グラフでは「余計な9こ」を切ってしまいます。
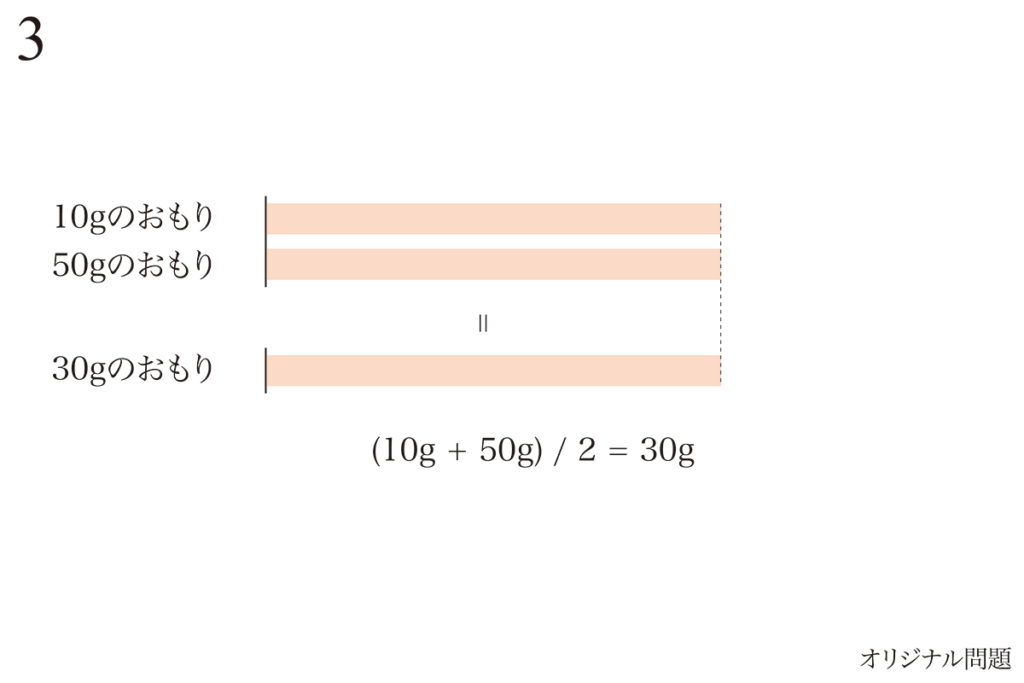
すると、「10gのおもり」と「50gのおもり」が同じ数となり、平均をとってまとめられます。
このように「未知数を減らす」考え方は算数的発想で、非常に柔軟で大事です。
方程式も良い面がありますが、小学生の頃には「小学生は小学生らしく」が最も良いでしょう。
「方程式を学ぶ」と問題が解けるようになる傾向があるのが現実です。
それは「方程式が便利だから」です。
そういう「便利さ」も良い面がありますが、「思考の柔軟性」は中学生以降も大事です。
「算数は算数らしい」柔軟な発想で、中学受験生の小学生には学んで頂くことを強くお勧めします。
次回は下記リンクです。
