前回は「算数の記述問題を解くポイント〜グラフや図を積極的に描く・記述を意識した学び・思考力を深めて学力アップ・矢印やメモ書きで簡単に表現・「考えていること」を明確化〜」の話でした。
「採点者に自分の考えを伝えること」が大事な記述問題
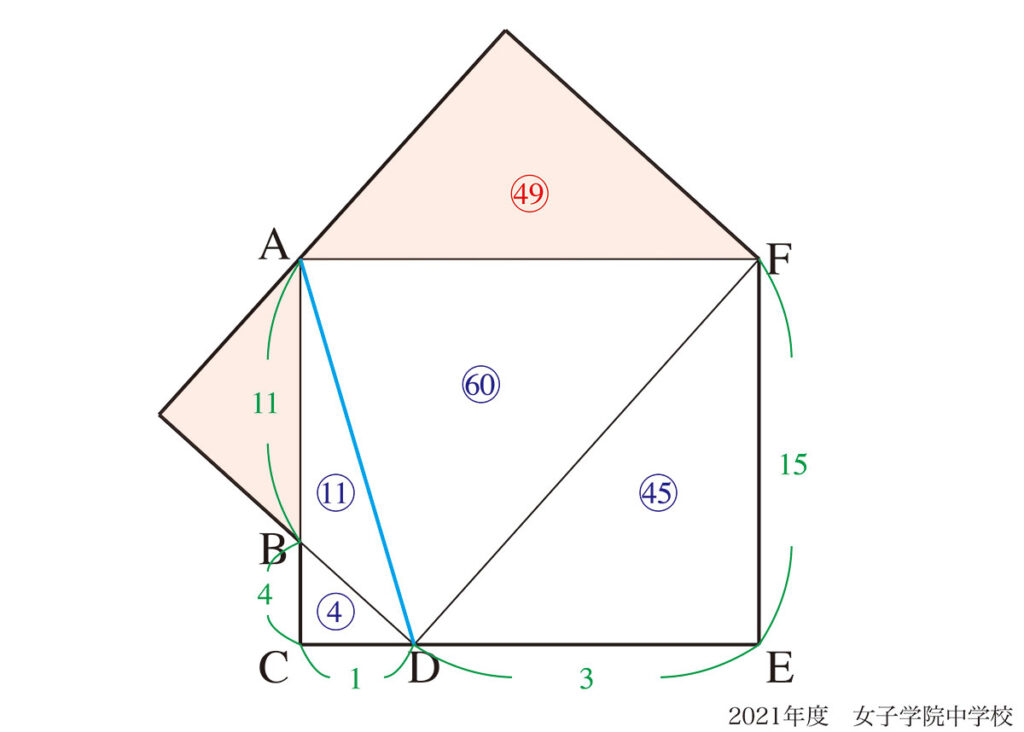
図形問題では「辺の比に応じて面積比を考える」ことがポイントになることが多いです。
上の図のように「補助線を引いて、ある部分の面積を〜とおいて・・・」と考えることが多い図形。
このような問題を解くとき、「答えだけ」の問題ならば「自分が分かっていれば良い」でしょう。
もし、同様な問題が記述問題の場合は、面積比と辺の比の根拠を書くと良いでしょう。
問題集の解答に上のような「面積比が一気に書いてある」時に、
男子小学生この部分とこの部分の面積比は、
どうやって分かったんだろう・・・
考え込んでしまうことがあると思います。
女子小学生そういうことは
時々ある・・・
女子小学生塾で先生が授業で教えてくれる時は、
順に面積を書いてくれるから理解できるけど・・・
女子小学生問題集でまとめて書いてあるときは、
「あれ？」って思う時が多い・・・
辺の比から面積比を求める時など「自分は分かる」ことが「他の人にも分かる」ことは意外と少ないです。
こういう時、問題集の解答を読みながら、
男子小学生ここが、こうなって、
だから・・・
具体的に考えることは、算数の思考力を上げるために大事なことです。
・「自分は分かる」ことが他の人にはスッキリと伝わらないことがある
・記述では「採点者に自分の考えを伝えること」が大事
考え方と解法の流れを書く：式の羅列に接続詞を追加
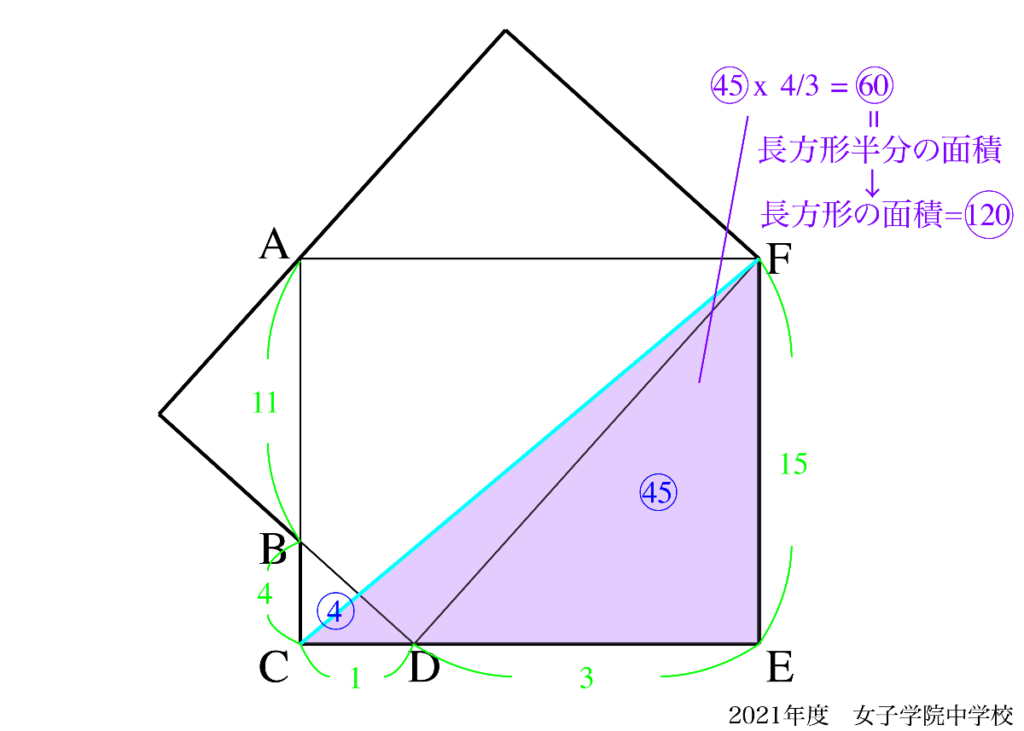
この図形問題では「長方形の面積の半分」を表すことがポイントです。
「長方形の面積の半分」を求めるのは、異なる補助線でも考えることは可能です。
記述問題である時、これが「ただ書き込まれている」と採点者は、
採点者う〜ん、分かっているような
気もするけど、ここの根拠が大事なんだよな・・・
採点者答えは合っているし、
出来てそうなんだけど・・・
採点者ここは明確に
書いて欲しかった・・・
大事なポイントを書かずに飛ばすと、場合によっては多少の減点があるでしょう。
中学・高校数学では、このように面積比等の根拠は明確に文章で書きます。
数学で使う言葉の「省略記号」をたくさん習うので、
男子中学生〜と〜と辺の比から、
AとBの面積比が分かる・・・
男子中学生ゆえに、〜の面積は〜となり、
求める面積〜を得る。
みたいにバリっとした文章を書きます。
高校数学では、数学の解答を書くときに「流れがはっきりしている」ことが非常に大事です。
高校生は数学の勉強をするときには「流れを明確に表現する」ことを意識しましょう。
解答の文章も「しっかり、はっきり表現する」ことが求められます。
そういう文章は「すぐに出来るようにならない」ので、ある程度の修練が必要です。
中学受験の算数では、そういう「バリっとした文章」は求められてないのが実態です。
そこまで「算数的・数学的表現」は必要ないでしょう。
そのような「しっかりした文章・考え方」は必要ないので、式の羅列に接続詞を追加しましょう。
・単なる式の羅列だけではなく、「だから」「なぜなら」など端的に説明
・流れを明確にすることは、思考力アップにつながる
ただ「式が羅列」してある場合、勘違い等で途中から間違えていると採点者は、
採点者ここは途中から
間違っているけど、どこが問題かな・・・
「どこで間違えたか」を探そうとします。
採点者はプロなので、
採点者あっ、ここで計算ミス
したっぽいな・・・
すぐに気付いてくれるでしょう。
「単なる計算ミス」なのか「分かっていない」ことが理由なのかが不明な場合があります。
その場合は、
採点者たくさん式を書いているけど、
良い点を上げられないな・・・
このようになってしまう可能性があります。
記述問題に限らず、接続詞を追加するだけで、考え方と解法の流れが明確になるでしょう。
「出来ない・成績が上がらない」から「出来る・成績が上がる」勉強法
基本的な問題は出来ても、応用問題で手が止まってしまうことがあります。
上のような文章題では、「文章をまず理解する」ことが大事です。
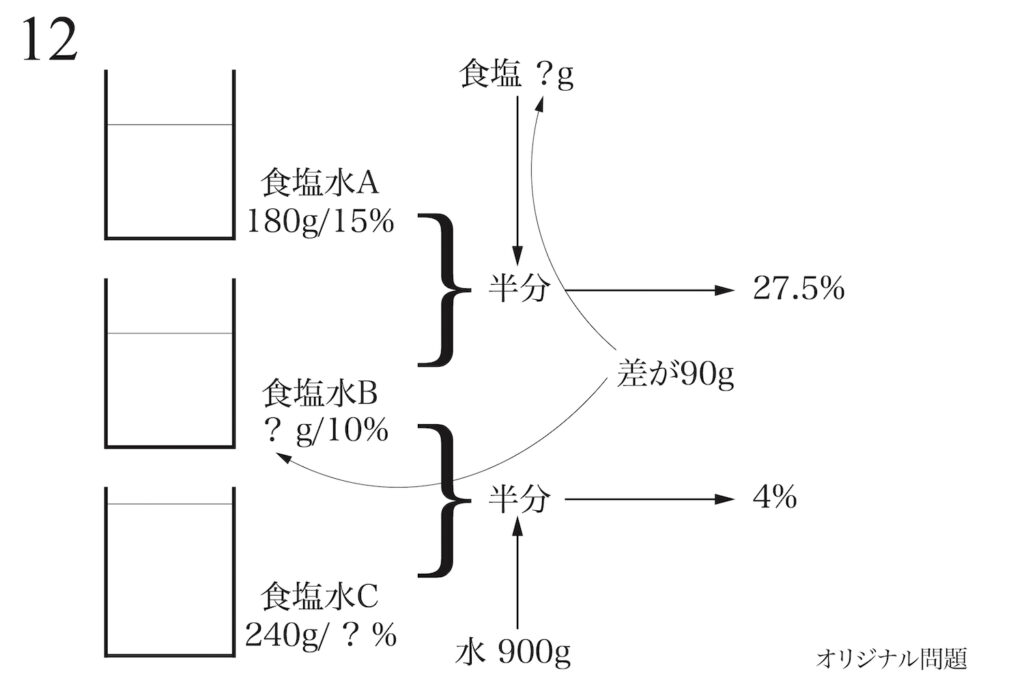
こういう文章題では、文章の状況を簡単に図解しましょう。
・状況を簡単な絵や図に描く→状況をしっかり理解
・大事な量・長さなどを記載して明確化
記述問題でなく「答えだけ」でも、このような図解を書くことは、思考が整理されます。
すると、「出来ない・成績が上がらない」から「出来る・成績が上がる」になるでしょう。
「丸暗記」ではなく、「数学的思考を表現する修練・訓練」と考えて、最初は答案を真似てみましょう。
慣れてくると、「自分なりの表現の仕方」が徐々にできてきます。
「何を考えているのか」を簡潔に示せば十分です。
男子小学生〜と〜は相似形
だから・・・
女子小学生〜と〜の面積比は
〜で・・・
簡単なメモでも良いでしょう。
・「考えていること」が明確になり、理解が深化する
・簡潔に書く姿勢が養われ、記述問題への対応力が上昇
ただ数式を羅列するのではなく、「何を考えているのか」を示せば良いのです。
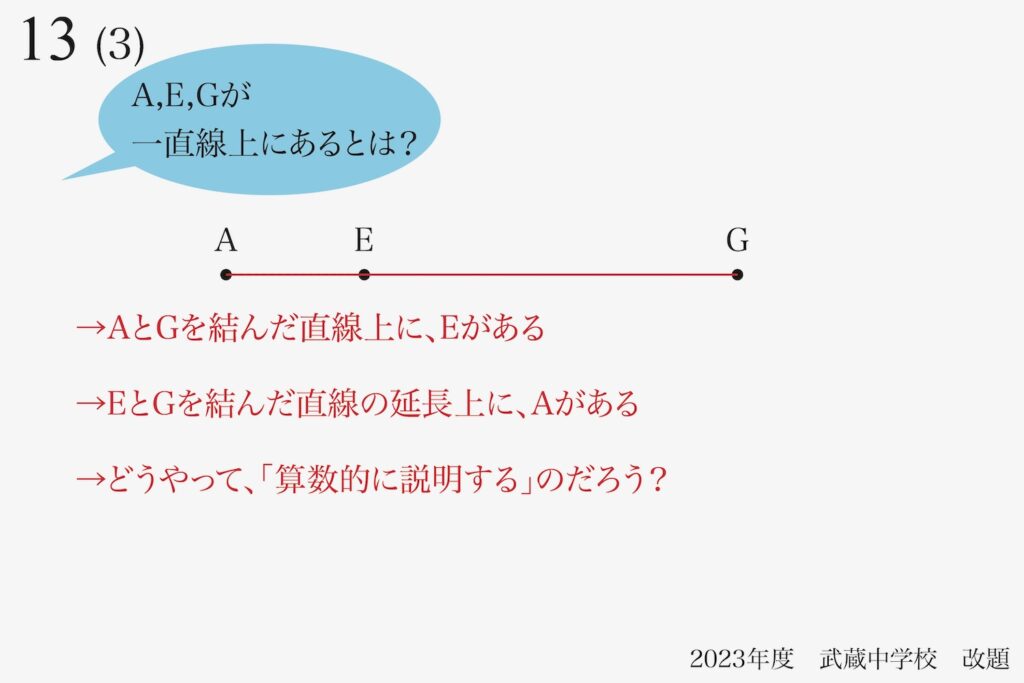
「3つの点が一直線にあることを説明」する話を上記リンクでご紹介しています。
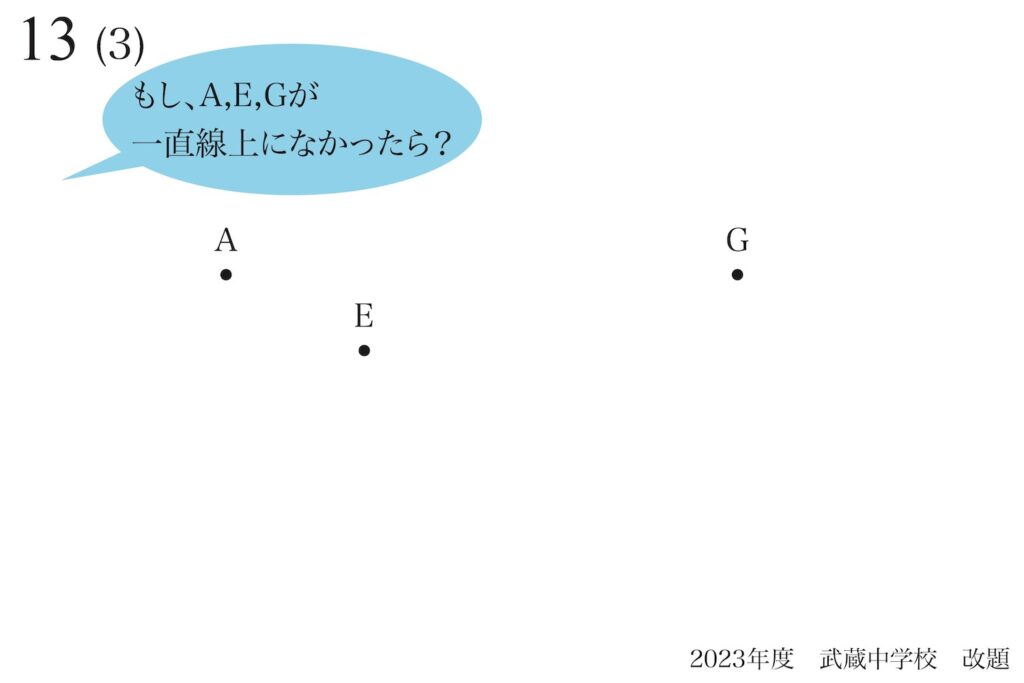
この時、「3つの点A,E,Gが一直線上になかったら」を考えました。
この「あることを示すために、そうではない状況を考える」ことは本質的です。
このことを文章で書くと、
採点者考える方向性は
良いな・・・
このように採点者は判断するでしょう。
中学受験では、これらのことが「きちんとした文章でなくても良い」と考えます。
例えば、記述の答案の一部に、
男子小学生もし、A,E,Gが一直線上に
なかったら・・・
「心の声」をそのまま書いても良いでしょう。
この「心の声」は大学受験では評価されない可能性が高いです。
一方で、中学受験では「思ったことが書いてある」場合、
採点者ああ、何か
考えているんだな・・・
採点者これは、ああ、
そういうことを考えているのか・・・
採点者何も書いてないよりは
良いな・・・
このように採点者は考えるかもしれません。
「何をどう評価するのか」は、各中学の教育方針・カラーによるでしょう。
白紙では採点者には何も分からないので、「思考のカケラ」でも何かを書くと良いでしょう。
文章ではなく、「単語の羅列」のような感じでも良いので、表現してみましょう。
思考が整理されて、学力も上がるでしょう。
「思考を整理する」ことは算数に限らず、全科目で非常に大事です。
特に、算数・理科では大事なことだと思います。
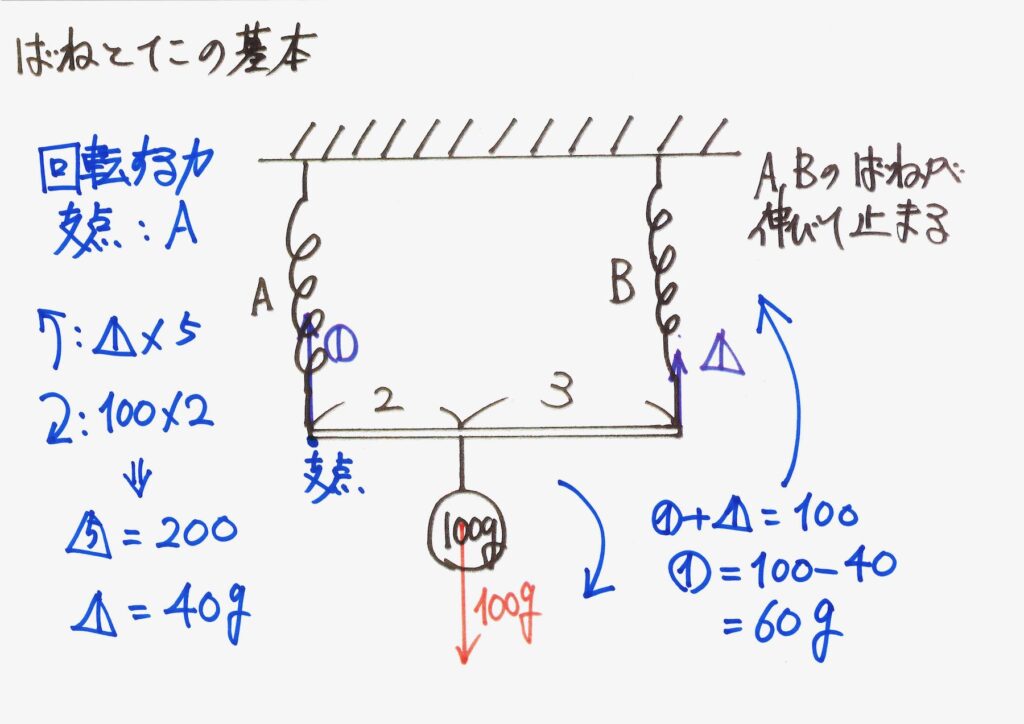
理科の電気・てこなどの問題は、しっかり図を描いて理解しましょう。
単に、
男子小学生こことここは
逆比で・・・
「ただ丸暗記」していると、応用問題が出来なかったり、間違える可能性があります。
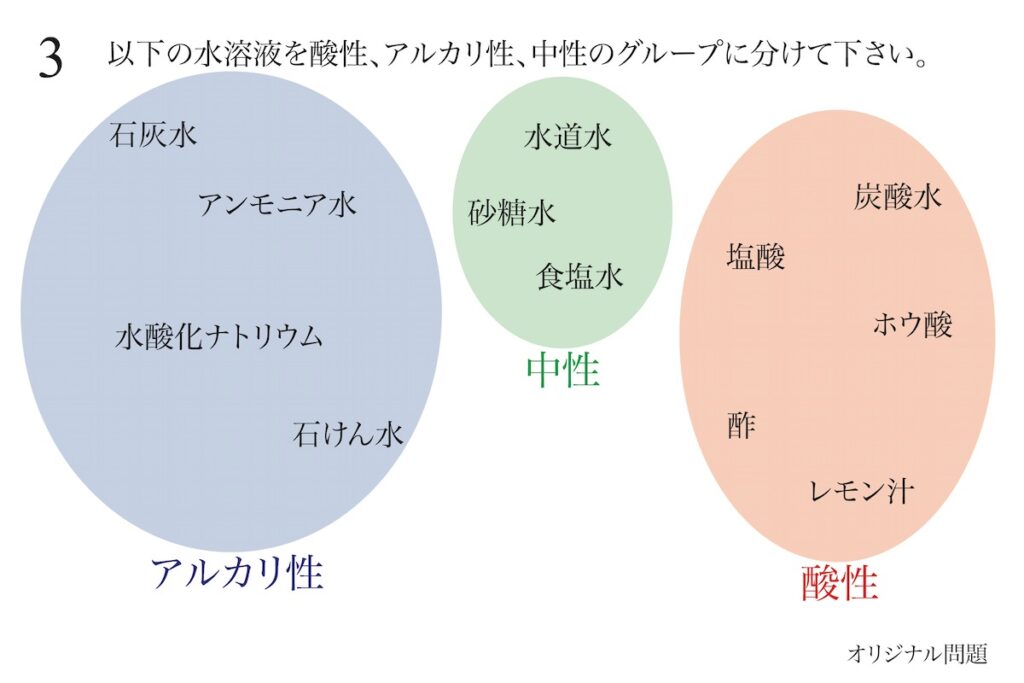
水溶液の性質は「丸暗記」でも良いですが、「同じ性質のイメージ」を持つことが大事です。
中学受験の算数では、文章題の中に旅人算・ニュートン算などの考え方があります。
それらの考え方をある程度学んで、ある程度出来るようになった後に難問に取り組むことが多いです。
その時、
男子小学生う〜ん・・・
これは、どうしたら解けるんだろう・・・
「手が止まってしまう」と「思考も止まってしまう」傾向があります。
大事なことは、「それらの考え方を応用する力」を育てることです。
そのためには、「学んだ考え方を整理して、進化させる」ことが大事です。
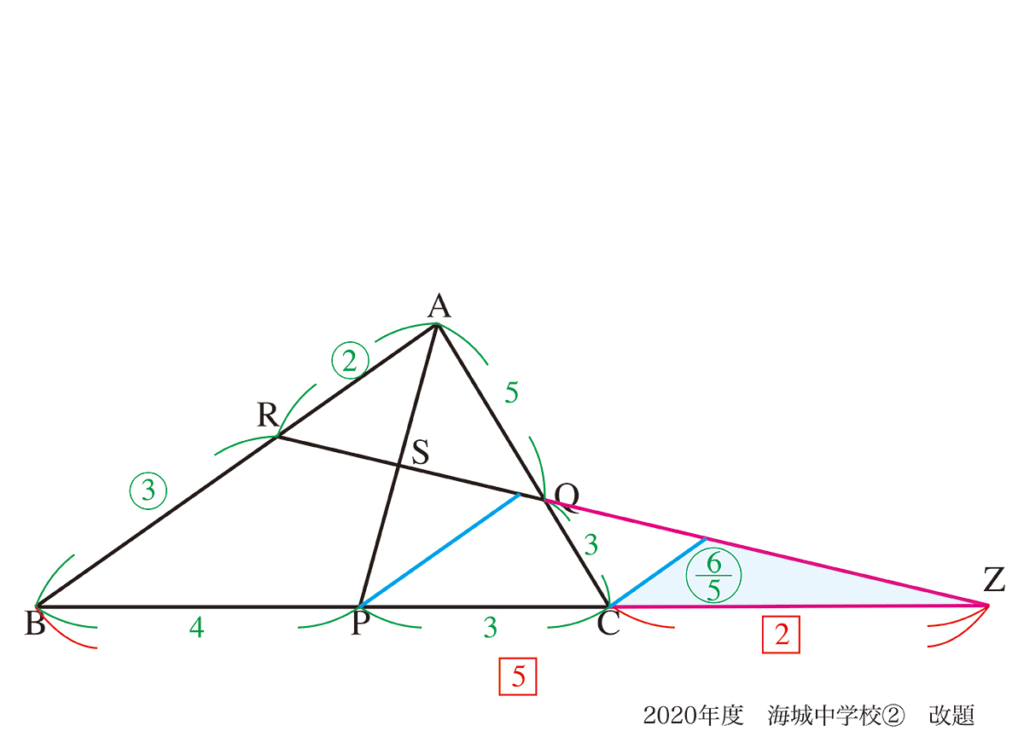
図形問題で、「図形の外側の世界に出る」ことは、「相似形をつくる」ことの応用です。
与えられた図形（世界）の中だけで考えずに、「世界を広げてみる」ことです。
これは、多くの図形問題において大変有用な考え方です。
「とにかく広げる」ではなく「どのように広げる」のか考えましょう。
あるいは「何に着目して広げて行くか」を考えてみましょう。
「なぜ？」をより強く意識しながら学ぶと、算数・数学・理科の学力は飛躍的に上がるでしょう。
次回は下記リンクです。
