前回は「算数の学力の飛躍的にアップする勉強法〜算数の学力停滞と突破する「きっかけ」・着実に答えに近づいてゆく姿勢・ドンドン進まずに「周りを見渡しながら」解く〜」の話でした。
算数の総合力を上げる勉強法：色々な角度から考える姿勢
各科目に共通しますが、「色々な角度から考える」視点を持つようにしましょう。
特に算数においては、
男子小学生ちょっと違う
視点はないかな・・・
他の考え方・解き方を考えてみると、応用力が広がるでしょう。
塾や参考書の解答を理解することも大事ですが、こうした視点を持つことは視野が広がります。
問題集の問題を解いてみて、
女子小学生なるほど、
こう考えればよかったのか・・・
このように理解して、その解法・解き方を習得することは大事です。
一方で、「解法・解き方を習得」の姿勢は「数多くの解法パターンの習得」の方向になります。
限られた時間で問題を解くには「解法パターンの習得」も大事かもしれませんが、
男子小学生この問題集のどこまで
解き方を頭に入れればいいのだろう・・・
際限がないように感じることもあるでしょう。
ニュートン算、旅人算、図形・・・と沢山の分野がある算数ですが、分野ごとに共通する軸があります。
解法・考え方は「問題に応じてある」ように感じられますが、この「思考の軸」を持つと強いでしょう。
実際、たくさんの問題を見てみると、
出題者この問題のここは、
こういう風にアレンジしよう・・・
出題者いや、この感じは〜中学で過去に出題されていたから、
こんな感じがいいかな・・・
出題者が様々なアレンジを加えているのが、「問題作成」の現実です。
「アレンジの仕方に応じて解法を習得する」のも一つの学び方ですが、大変です。
女子小学生そういえば、
この間、似た問題でこう考えていたけど・・・
女子小学生同じように
考えられないかな・・・
・分野ごとに共通する「考え方=思考の軸」を考える
・問題ごとのバリエーションの違いは「同じ」と考えられる思考力育成
共通する「考え方=思考の軸」があれば、「バリエーションの違いは同じ」と考えられます。
視野が広がって問題・物事を多角的見れるようになり、特に受験期後半以降学力が上がるでしょう。
複雑な形と単純な形：合体と分解
戦艦大和のペーパークラフト作成の話をご紹介しました。（上記リンク）
非常に時間がかかり、地味な作業がたくさんあった戦艦大和のペーパークラフト作成。
内野吉貴子どもと一緒に作成して、
30時間くらいかかりました。
結構時間がかかり大変でしたが、「パーツの成り立ち」が分かりました。
戦艦大和は、非常に複雑なデザインです。
船体の曲面は非常に複雑な形状で、模型を作成するのが一苦労でした。
紙で作ることが「とても大変」であるので、これを鉄板で実際に作成する困難は想像を絶します。
その困難を成し遂げた戦艦の設計者・技術者の方々の力量は大変素晴らしいことです。
この戦艦が実際に動き、極めて強固な防御力を持っていたことを考えると、不思議な感慨を感じます。
船体の局面は非常に複雑ですが、パーツは比較的単純な円筒であったり多角形である部分もあります。
非常に複雑な部分もありますが、中には「単純な形が組み合わさってできた部分もある」のです。
戦艦大和の主砲である大きな大砲の台は、円筒形でした。
それらの円筒形を組み合わせて、たくさん配置すると「複雑な形」になります。
つまり「単純な形が合体すると複雑になる」ことがあります。
同様に「複雑な形を分解すると単純な形になる」ことがあります。
・単純な形が合体すると複雑になる
・複雑な形を分解すると単純な形になる
図形問題の「思考の軸」：比とは「比較する」こと
受験生はプラモデルを作成する時間はありませんから、
男子小学生最近、勉強ばっかりで
プラモデル作ってない・・・
今まで作成したプラモデルをイメージしてみましょう。
男子小学生受験終わったら、
プラモデル作る！
そして、「合格後にプラモデルを作る」ことを考えてみましょう。
あるいは、本記事の写真をご覧になってイメージするのも良いでしょう。
図形問題では「解答の補助線以外にも考えてみる」のも良いでしょう。
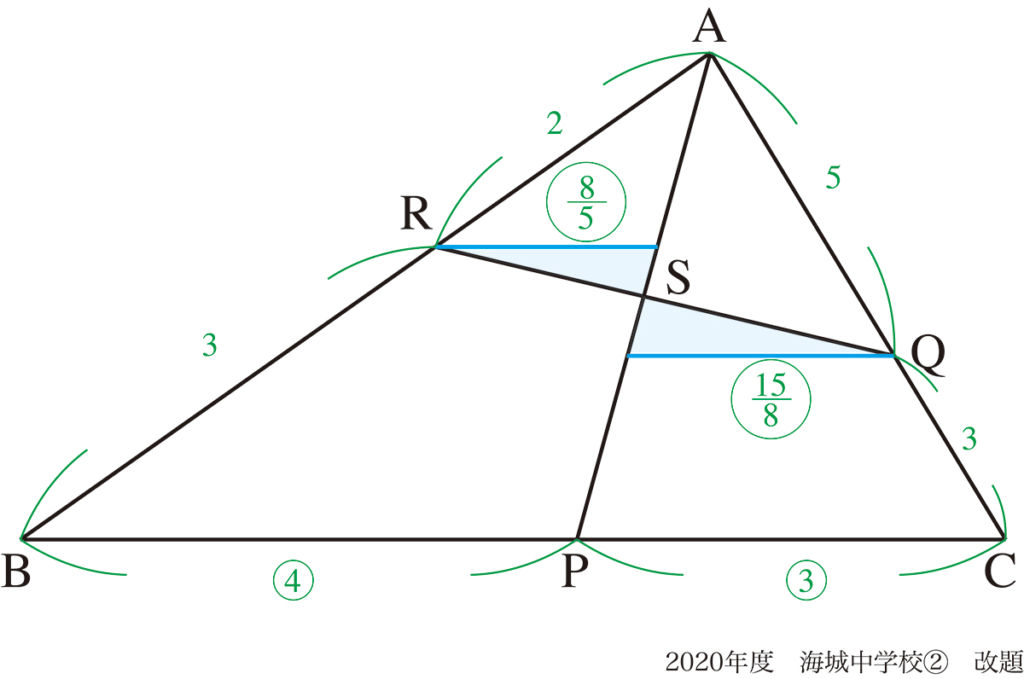
上の問題（算数実践紀行）では、辺の比と面積比で考えてみました。
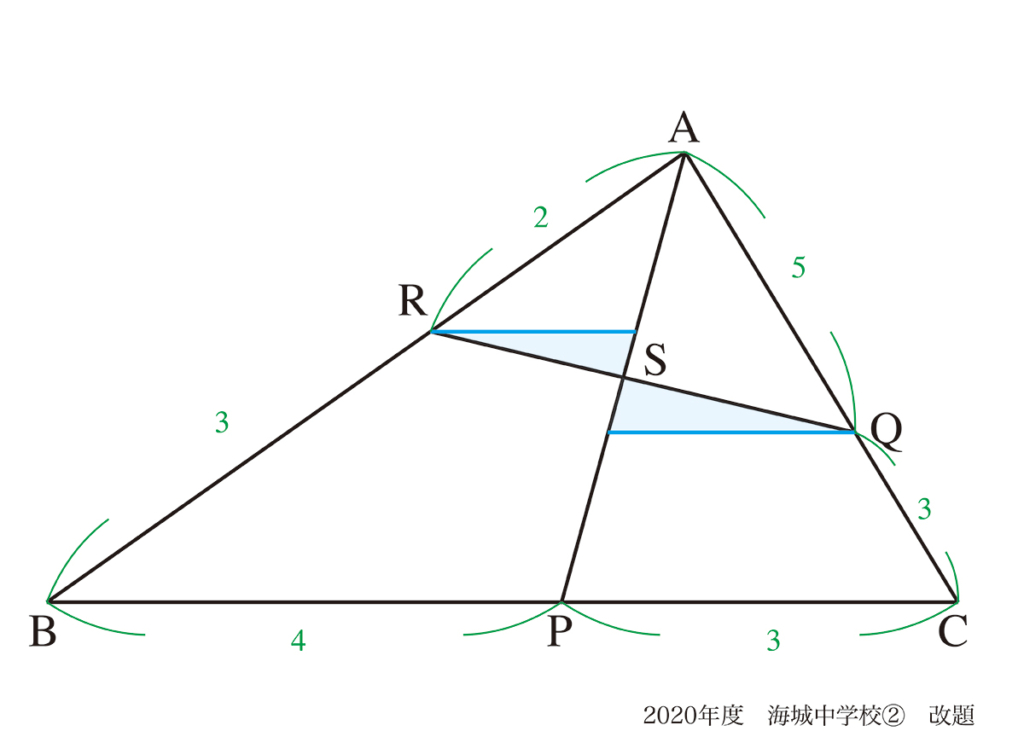
これらの辺の比と面積比は「面積と長さで考える次元が異なる」ので全く違う視点です。（上記リンク）
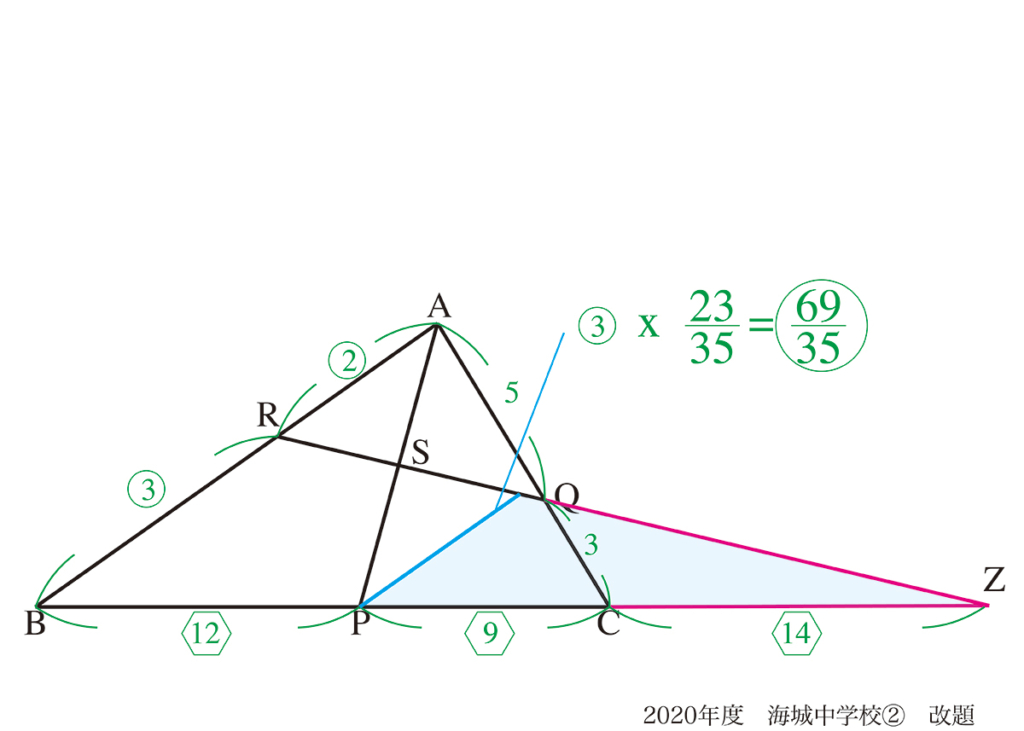
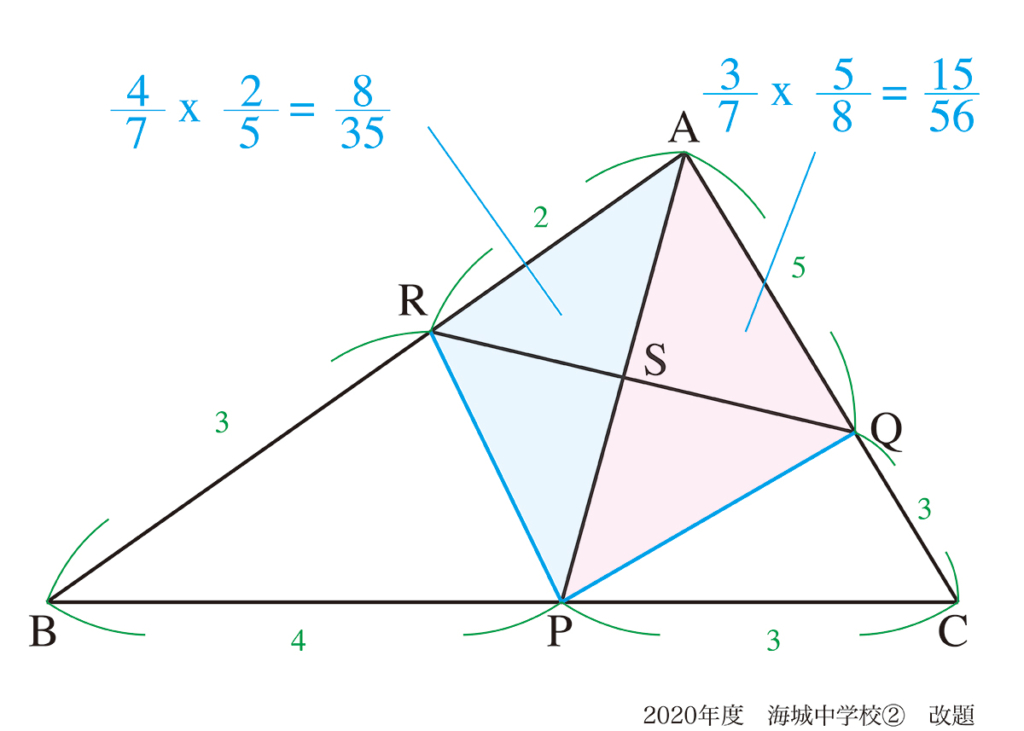
「全く違う視点」ですが、共通する軸があります。（上記リンク）
・辺や面積の比に注目
・比は「比較すること」で「何を、どう」比較すれば答えに近づくかを考える
比の問題は沢山あり、各分野を横断する考え方です。
そもそも比は「比較すること」です。
歴史で、昔の役人で国試がいますが、「国司=国を司る（つかさどる）」で、言葉自体に意味があります。
旅人算で、
男子小学生A君とB君の
歩く速さの比は 5: 3で・・・
このように「比を考える」時は、「A君とB君を具体的に比較」しています。
「思考の軸」には共通点がありますが、補助線は異なります。
「補助線が異なる」と「全く異なる解法」にも感じられますが、「比較する姿勢」は同一です。
このように「この補助線に気づかなければ解けない」ことはなく、様々な補助線もあります。
どちらが「良い補助線」かは様々な意見がありますが、両方とも「解ける補助線」です。
「時間が限られている試験」では、「素早くできる解法」の方が良いです。
少し遠回りしても「きちんと出来る」ことも大事です。
受験期後半以降は「この補助線でなければ解けない」という思考法ではなく、
男子小学生他にもあるはずで、
これはダメかな？
このように「この補助線ではどうだろう？」と考えて、取り組んでみましょう。
女子小学生この補助線でも
良さそうだけど・・・
女子小学生あれ？
上手くいかない・・・・
女子小学生何が良くなくて、
解答の補助線は何が良いんだろう・・・
自分なりで良いので、補助線を比較してみると良い勉強になるでしょう。
すると、図形問題の発想が広がり、学力・成績が上がるでしょう。
次回は下記リンクです。
