前回は「てこのつり合いのコツ・考え方 3〜生活に役立つ理科の学び・身の回りの生活への好奇心・「てこ」は何に役立つか?・ピラミッドと安土城の石の運搬・どうやって「重いモノ」を運ぶか?〜」の話でした。
てこの原理のイメージ:「てこ」と加藤清正の熊本城
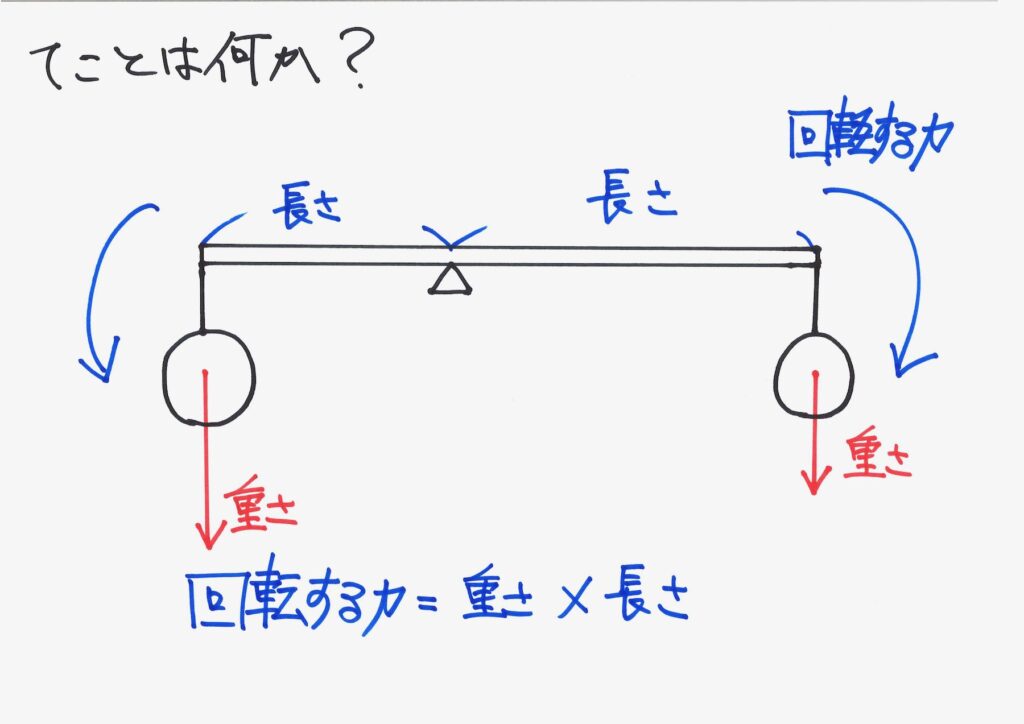
最も基本的な「てこの棒一本、おもり2つ」のてこ。
 男子小学生
男子小学生これは、
簡単だから、出来るよ!



でも、てこの棒やおもりが
多い複雑な問題が苦手・・・
バネなどは「働く重さ・力」を考えれば、問題は解けます。
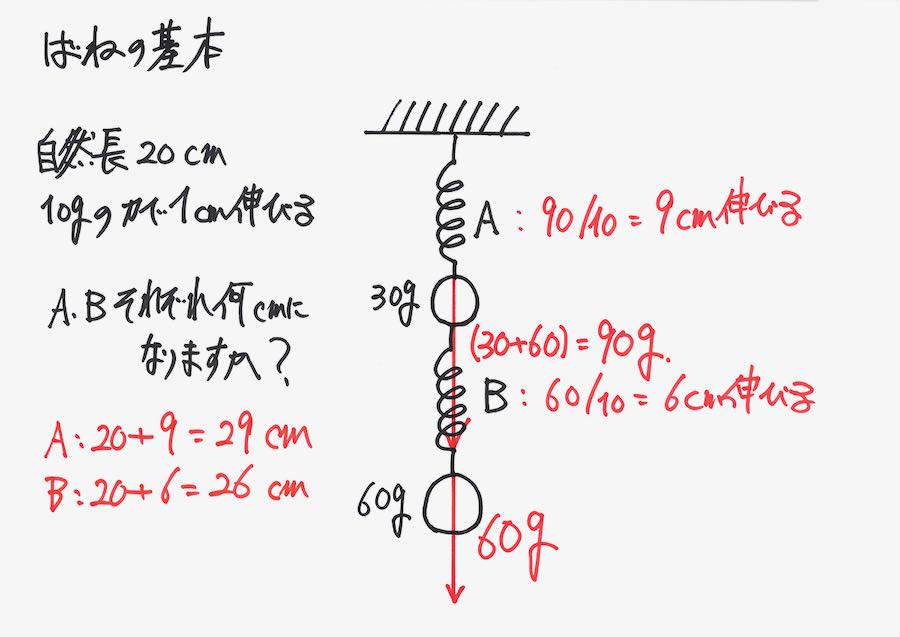

バネに関しても、今後複雑な問題を考えてゆきますが、「重さ・力」を考えれば出来るバネ。
・バネの直列:そのバネの下にある、おもりの重さの合計の重さがかかる
・バネの並列:そのバネの下にある、おもりの重さの合計を分けた重さがかかる
それに対して、てこでは、新たに「モーメント」を考えます。
・モーメントは「回転する力」
・「力 x 長さ」でグルッと、何かを回転させるイメージ
モーメントは、難しく考えずに「グルッと回転させる力」のイメージです。



でもさ、なぜ、てこでは
モーメントが出てくるの?



バネでは
出てこなかったのに・・・



確かにそう・・・
バネと一緒の考え方なら良いのに・・・



考えなければならないことが
増えて困るかな・・・
このように考えるのが「自然」であり、このように「なぜだろう?」と少し考えることも大事です。


ピラミッドのような雄大な建築でも、日本の城郭建築でも、たくさんの石を使います。


日本の城郭建築の石垣の作り方は、独特な工法です。
戦国時代〜江戸時代にかけて、当時様々な大名・大工たちがその技術を競いました。


熊本城を築いた加藤清正を、ご存知の人もいるでしょう。



加藤清正なら
知っているよ!
猛将として知られる加藤清正は、羽柴(豊臣)秀吉の遠い親戚です。
それが縁で秀吉に仕えた加藤清正。


メキメキ頭角を頭角を表して、羽柴・豊臣家最重要人物の一人となります。
晩年には豊臣秀吉のタガが外れてしまい、朝鮮出兵を強行しました。



蔚山(うるさん)では、
死にかけた・・・



我が国へ
生きて帰れた・・・



本当に、
本当に良かった・・・
当時、鉄砲先進国であり、戦国時代で戦い続けていた日本軍は、世界最強国の一つでした。
この猛烈なパワーで、朝鮮半島を瞬く間に席巻します。
ここで、大軍勢の明(中国)軍に猛烈な反撃をされて、加藤清正軍の将兵は「生死の境」を経験します。
軍人としても優れていた清正は民政・内政にも手腕を発揮し、城郭建築の名手でした。
「なぜだろう?」と考える姿勢:モーメントと「回転する力」
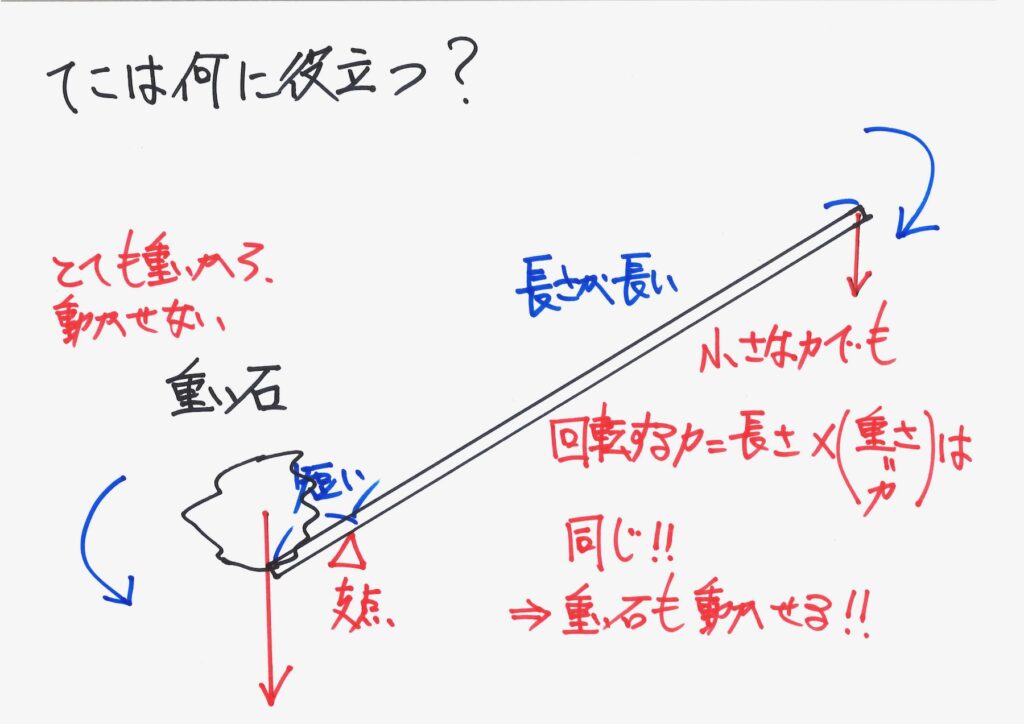

そして、石垣の大きな石を動かして、工事するためには「てこの原理」が便利でした。



それは、
分かるよ・・・



でも、なんで突然「てこ」とか
「モーメント」が出てくるの?
実は、「モーメント」は、てこなどで登場するのではなく、「もともと大事なこと」なのです。



えっ!
そうなの?


皆さんの身の回りの家や住まい。
木造建築でも鉄筋コンクリート造・鉄骨造の建築でも、力とモーメントを考えて構造を作ります。
・力(重力)、重さなどのつり合い
・モーメント(回転する力)のつり合い
そのため、「力、重さのつり合い」だけではなく、必ず「モーメントのつり合い」も考えます。
ですから、バネは「モーメントがなかった」のではなく、「モーメントを考える必要がなかった」です。
バネの問題でも「モーメントを考慮する」こともできますが、多くは「力、重さ」だけで解けるのです。



そういうこと
だったんだ・・・



モーメントは、
「てこ」とかだけではなく、一般的なことなんだね。
てこに限らず、非常に大事で、力と同様に「基本的で大事な」モーメント(回転する力)です。



こういう問題は、
こう考えましょう!



こういう問題は、
このパターンで!
こう教えられると、



これは
なぜだろう・・・
「なぜ?」を考えることが少なくなり、



とにかく、
この解法・パターンを身につけよう!
この様に「解法やパターンを身につける」と考えがちです。
そうした中でも、ふとこうした疑問を持ってみることは、理解の助けになります。
長期的視点では、「好奇心を持つ姿勢」は成績アップにつながるでしょう。
つり合う時とつり合わない時
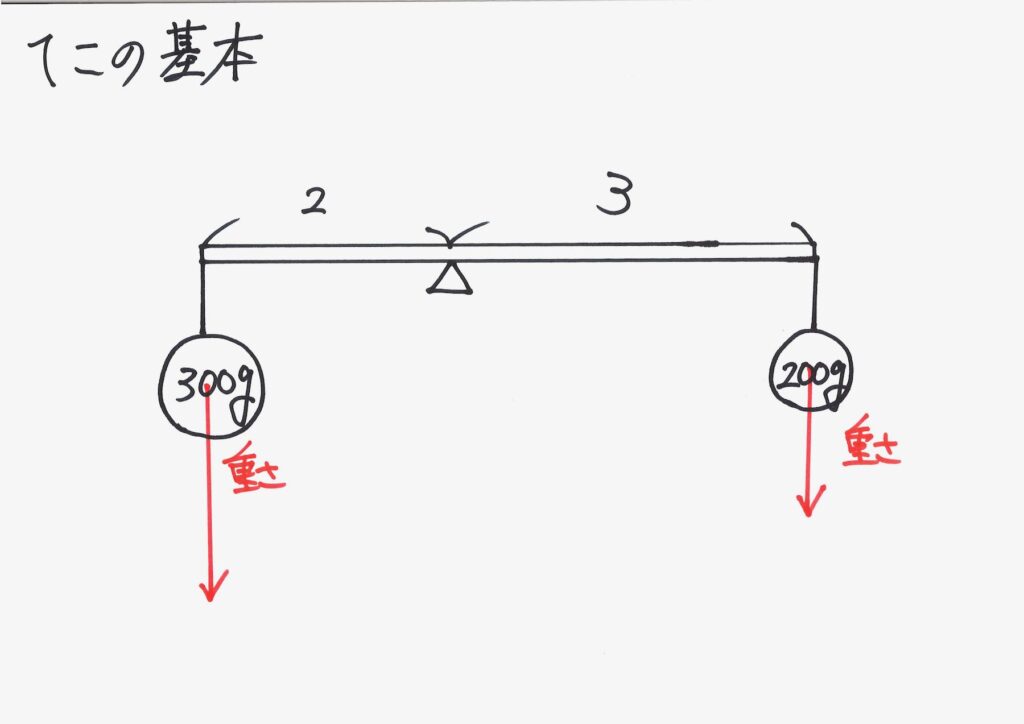

「てこの公式」だけではなく、具体的なイメージを考えましょう。
おもりに重さがかかりので、「赤い矢印」などで描きましょう。
最初の頃は、色鉛筆・マーカーなどで描いてみると良いでしょう。
慣れると分かるようになるので、鉛筆でも良いでしょう。
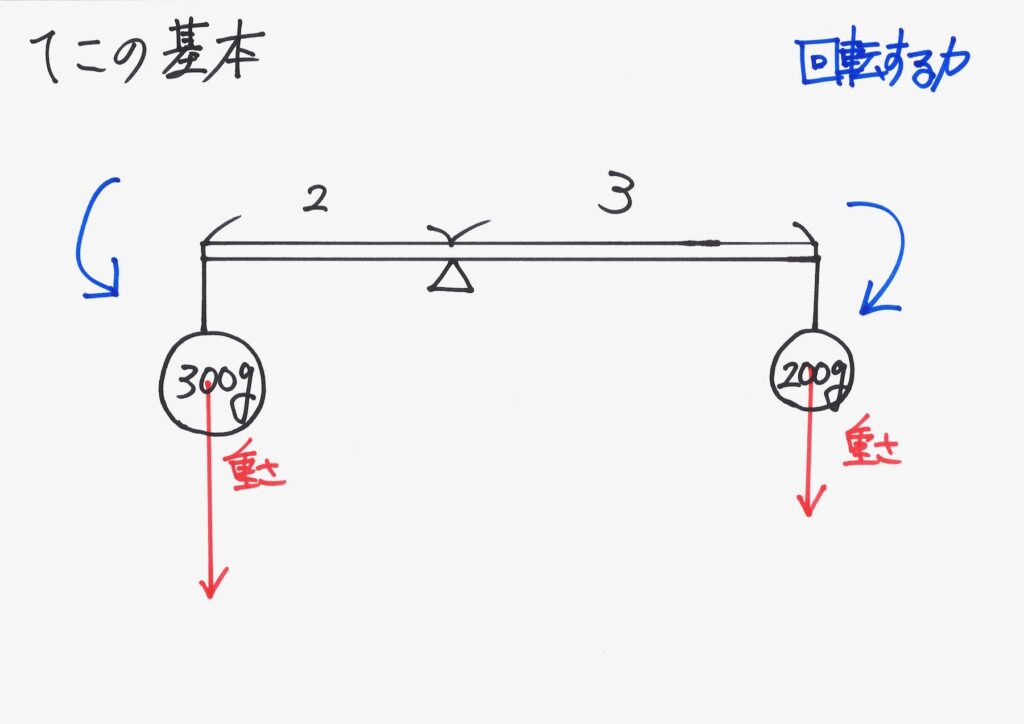

そして、「長さ x 力(重さ)」の回転する力が掛かる状況を「青い矢印」で表現します。
これをしっかり描いて、「左側のおもりと右側のおもりがあると、どうなるか」をイメージしましょう。
下向きの力を合計した「500g分の力(重さ)」は、支点が負担しています。
そして、左側のおもりが「反時計回りのグルッと回転する力」をもたらします。
同じように、右側のおもりが「時計回りのグルッと回転する力」をもたらします。
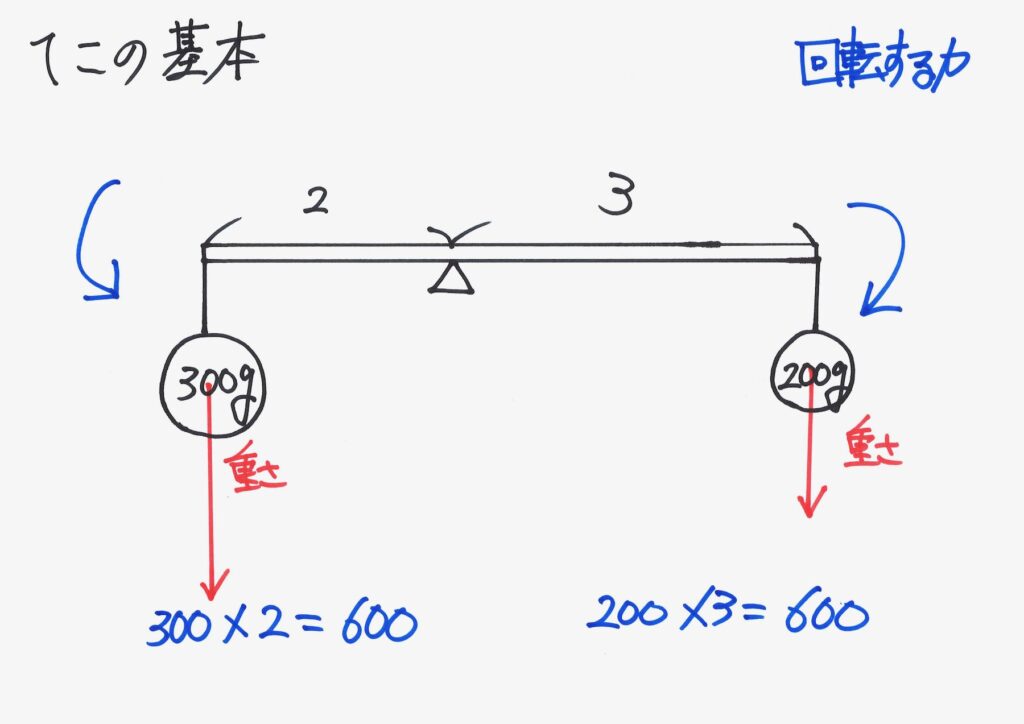

左右それぞれの「回転する力」を、計算しました。
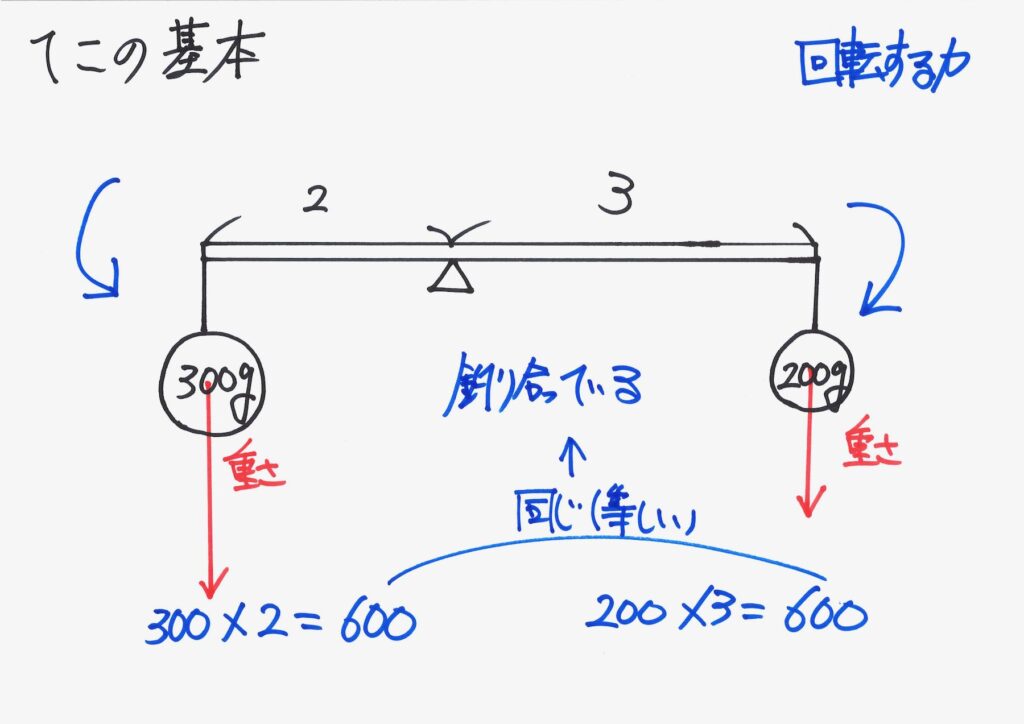

「回転する力」が同じ(等しい)」ので、釣り合いが取れています。


問題で考えるときは、大抵は、このように「釣り合う時」です。
現実的には「つり合わない」方が普通で、「つり合うこと」は珍しいのです。
上皿てんびんで「小さな分銅」でつり合いを取るのは、なかなか難しいです。
そして、「つり合わない」状況になることが多いです。
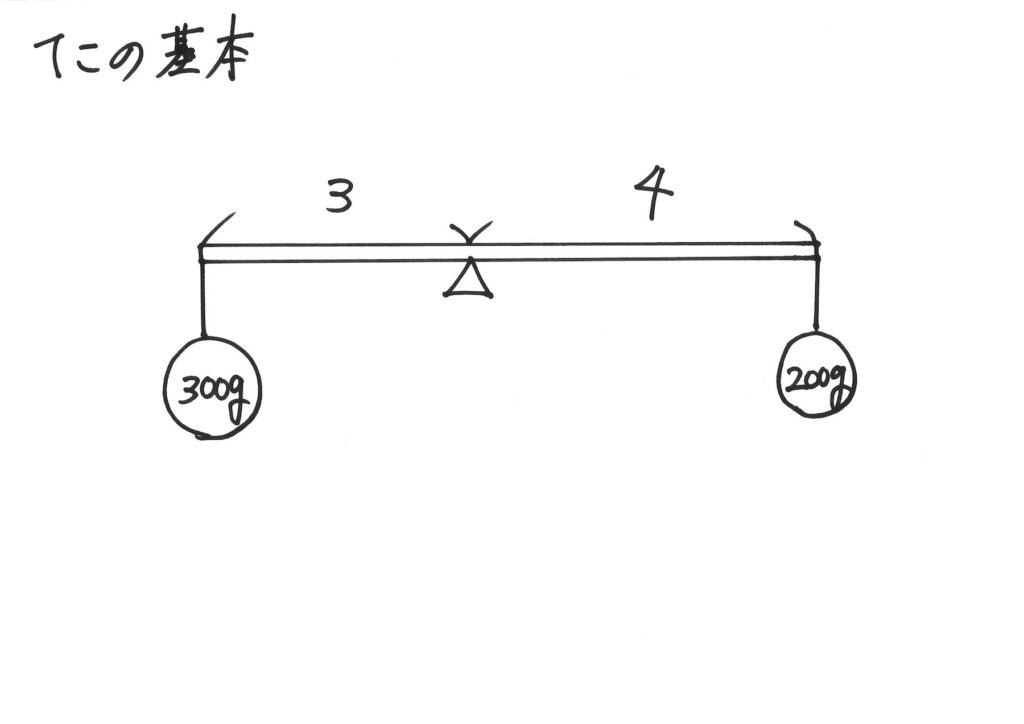

上記のような、てこを考えましょう。
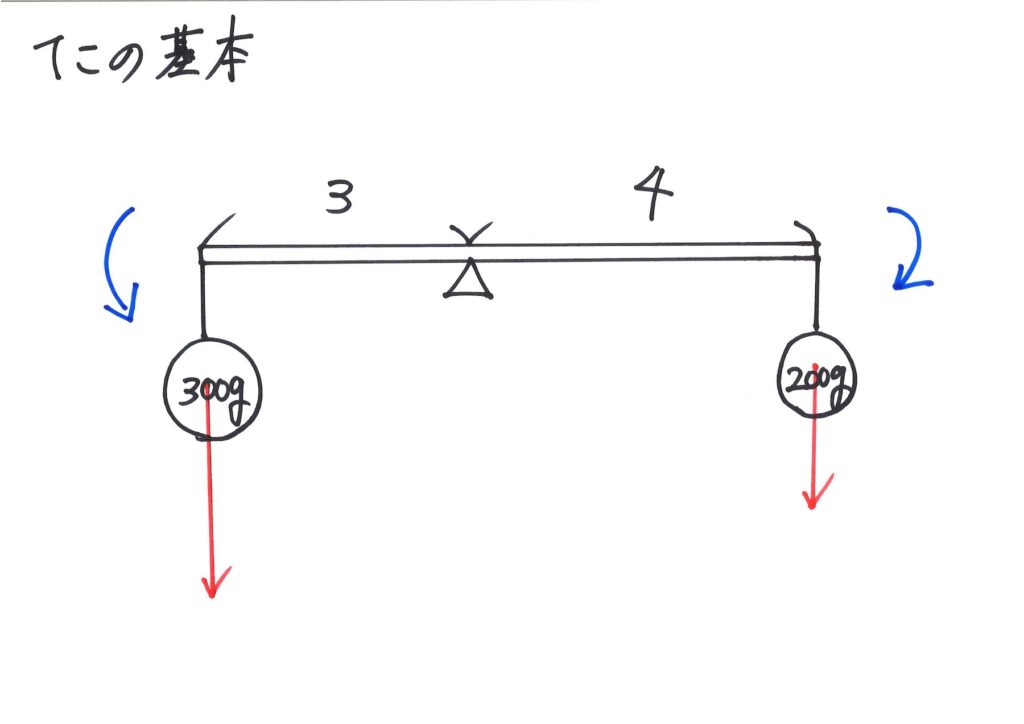

おもりに重さがかかり(赤い矢印)、回転する力(青い矢印)が掛かります。
これらの矢印を「パパッと」描くようにしましょう。
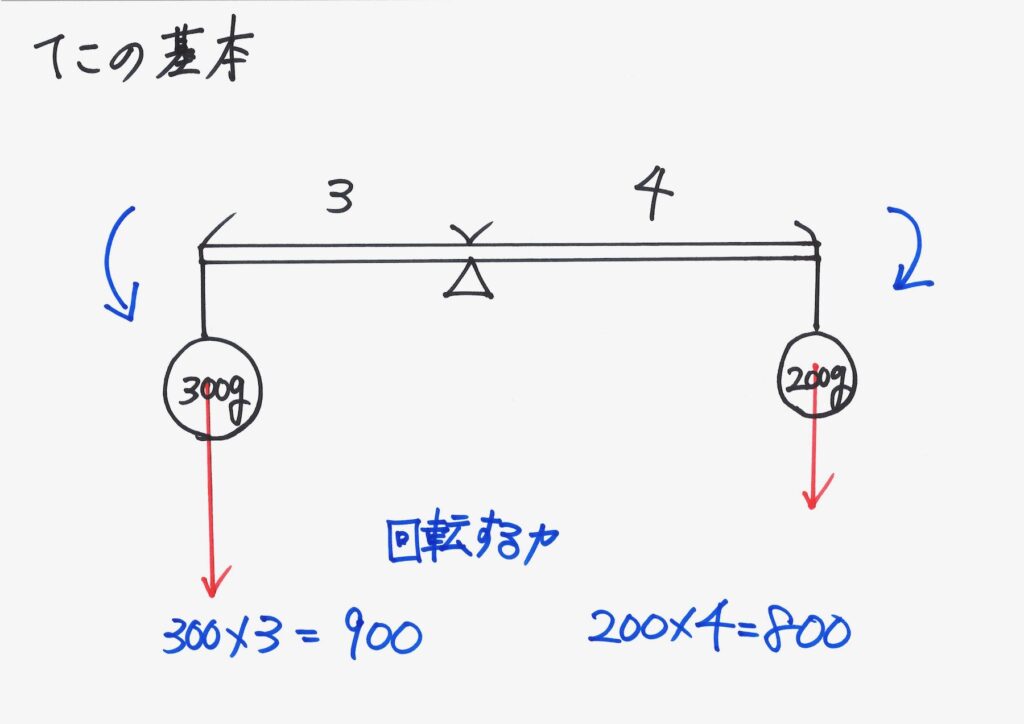

「回転する力」を計算すると、左側(反時計回り)の方が大きいです。
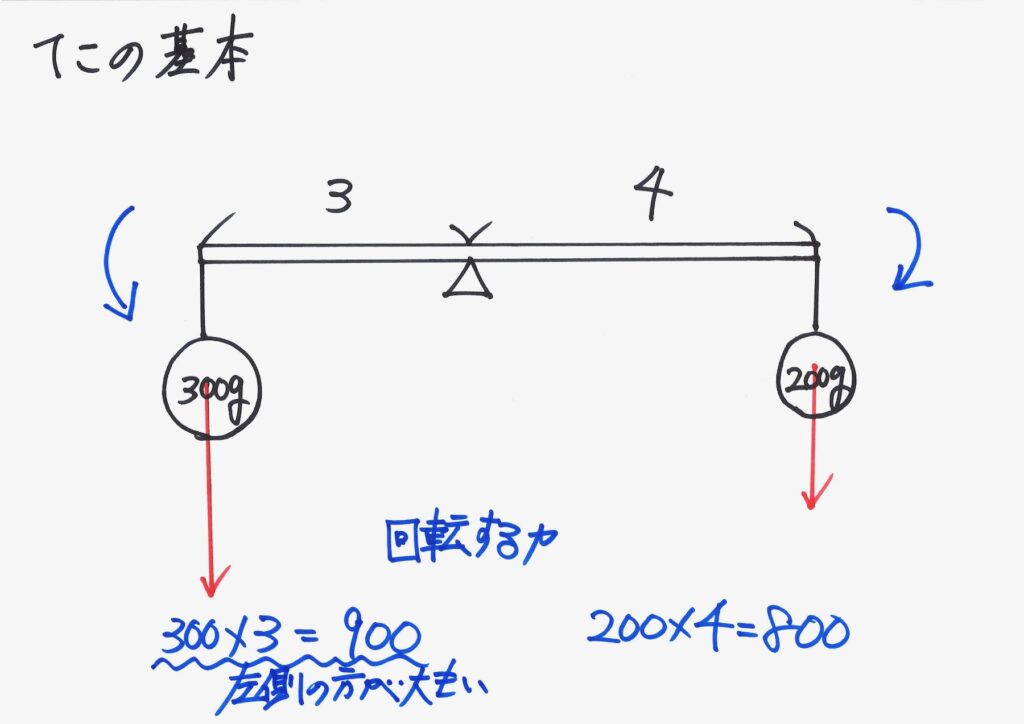

つまり、「反時計回りの回転する力」の方が強いのです。
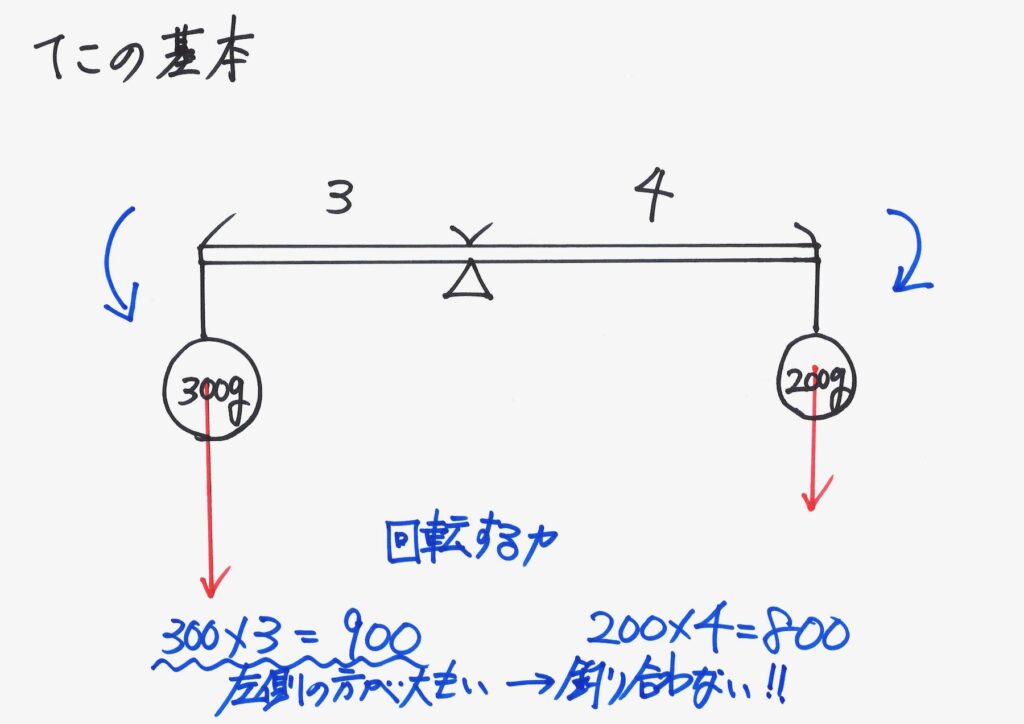

「釣り合わない」ことになります。
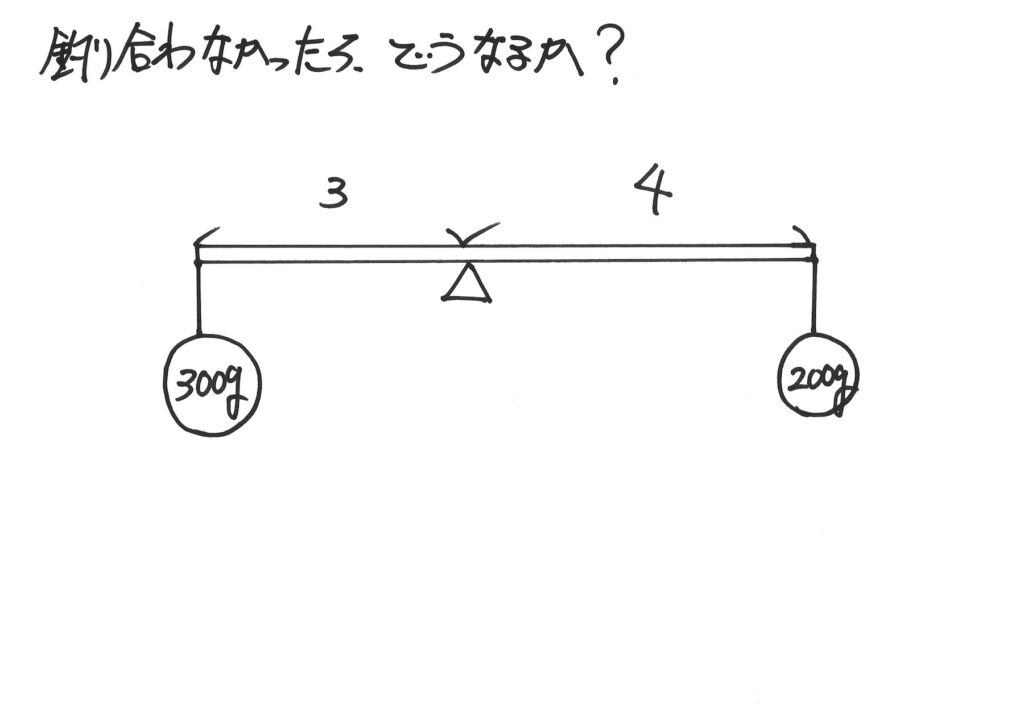

それでは、「釣り合わなかったら」どうなるか、考えてみましょう。
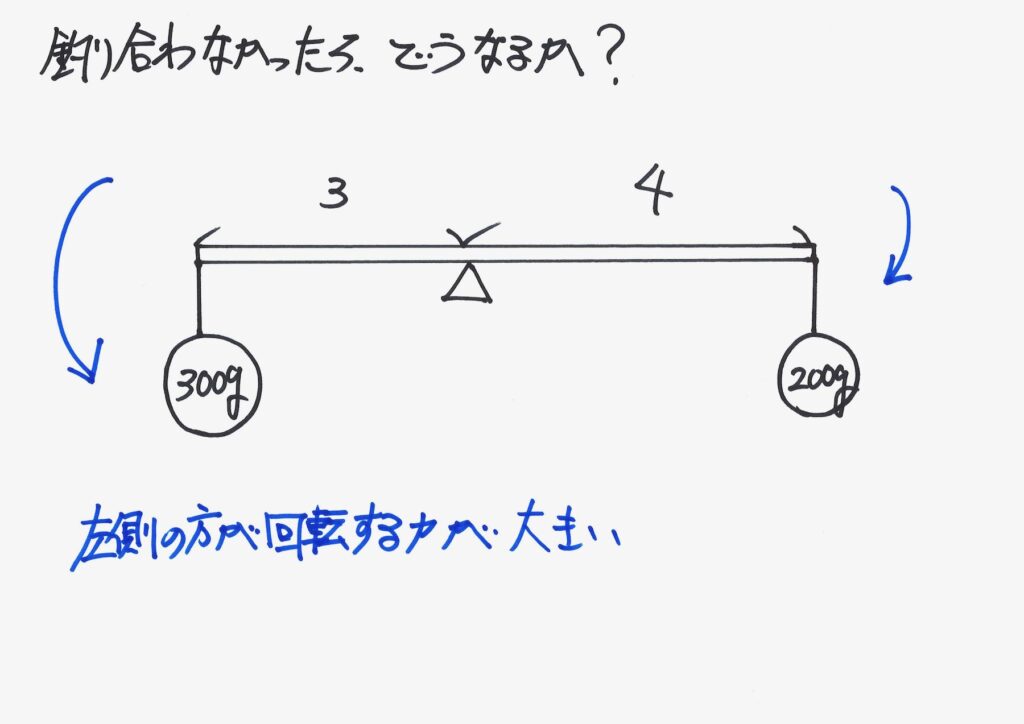

二つのおもりがそれぞれ、「回転する力」を作ります。



これは、分銅のてんびんと同じように
考えればよいかな?



そうよね。
状況は似ているよね・・・



そしたら、
左側が下がる、かな・・・
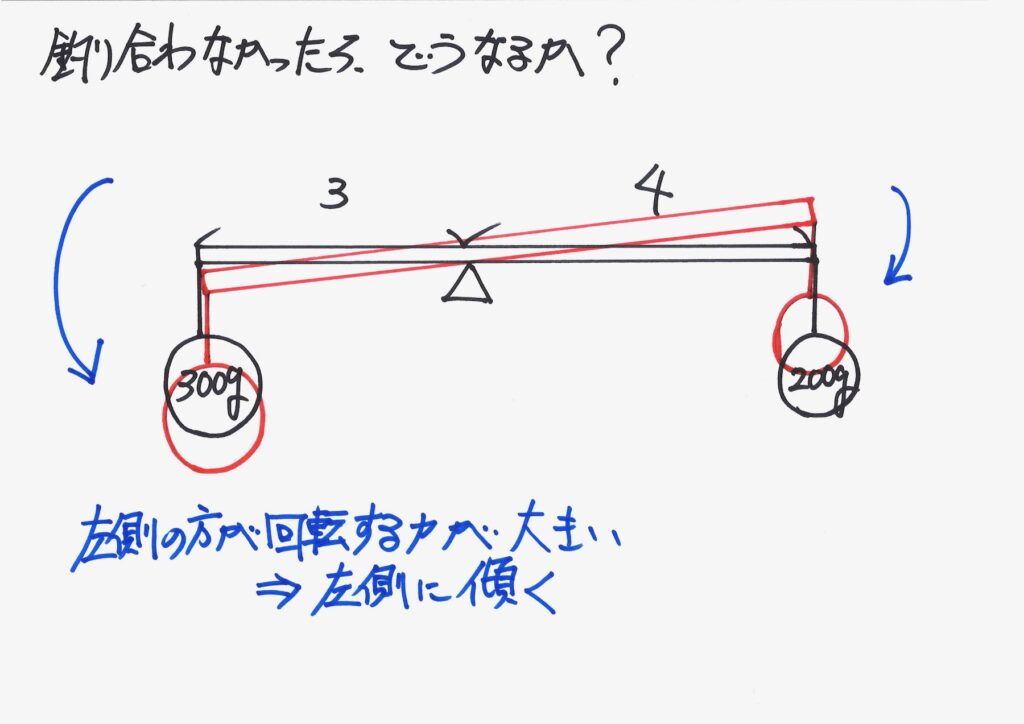

「左側の、反時計回りの回転する力」の方が、大きいので、左側に少し傾きます。
問題文などで、てこが登場すると「当然のように水平につり合っている」ことが多いです。
ところが、「モーメント(回転する力)」がつり合ってなければ、「水平にはならない」のです。
「つり合うことが前提」となっていることが多い「てんびんやてこ」の問題。
「つり合っている」ためには、「つり合う条件が必要」であることを、しっかり理解しましょう。



「つり合う」イメージを
持って考えるんだね。



「つり合う」ことって
あまり考えなかった・・・
「てこ」やおもりが沢山登場する複雑な問題でも、この基本的な「つり合う」状況を考えましょう。
すると、様々な問題でもイメージして、解くことが出来るようになるでしょう。
次回は下記リンクです。


