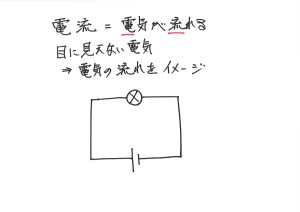
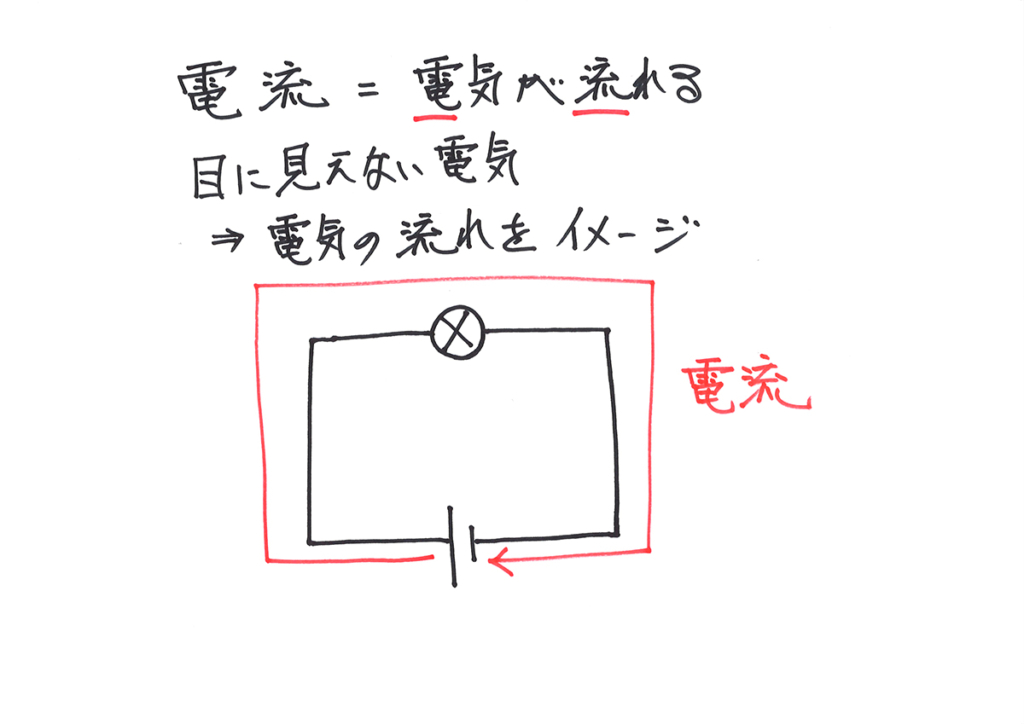
前回は「電気・電流のわかりやすい考え方・コツ 1〜電圧と電流と抵抗・電流とは?・流れる電流を描く・電池とは?・電流を「持ち上げる」役割〜」の話でした。
直列と並列:理由を理解して暗記
前回のイメージを考えながら、直列電池を考えましょう。
 男子小学生
男子小学生知ってるよ。
電池を2個直列だと、電圧が2倍だよね。
そのイメージを暗記ではなく、しっかりイメージしてみましょう。



暗記した方が
早いよ・・・
確かに「暗記した方が早い」のですが、なぜ「2個直列だと、電圧が2倍」なのでしょうか?



なぜ?は
考えたことがないよ・・・



電池2個直列だと電圧2倍、
並列だと電圧1倍、って習ったよ・・・
電池の直列・並列は暗記する方が良いですが、理由を理解して暗記しましょう。



「理由を理解して暗記」は、
ただの「暗記」とは違うの?
「ひたすら暗記」すると基本問題は解けますが、少し回路が複雑になると解けなくなることがあります。
そのため、「理由を理解して暗記」する方が良いでしょう。
ひたすら「暗記」すると、勉強が楽しくなくなります。



確かに、暗記ばかりだと
つまらなくなるかも・・・
そして「暗記に頼る」勉強法だと、記述式問題に対応する力が育ちにくいです。
「答えのみ」や選択式の問題が多い場合でも、「パターン分け」で考えて解くと、



これは、あのパターンだから、
これが答えかな・・・



あれ・・・
違った・・・
ちょっと状況が異なると、出来ないことがあります。
そこで、「電池が電流をエイッと持ち上げる」イメージを持ちましょう。
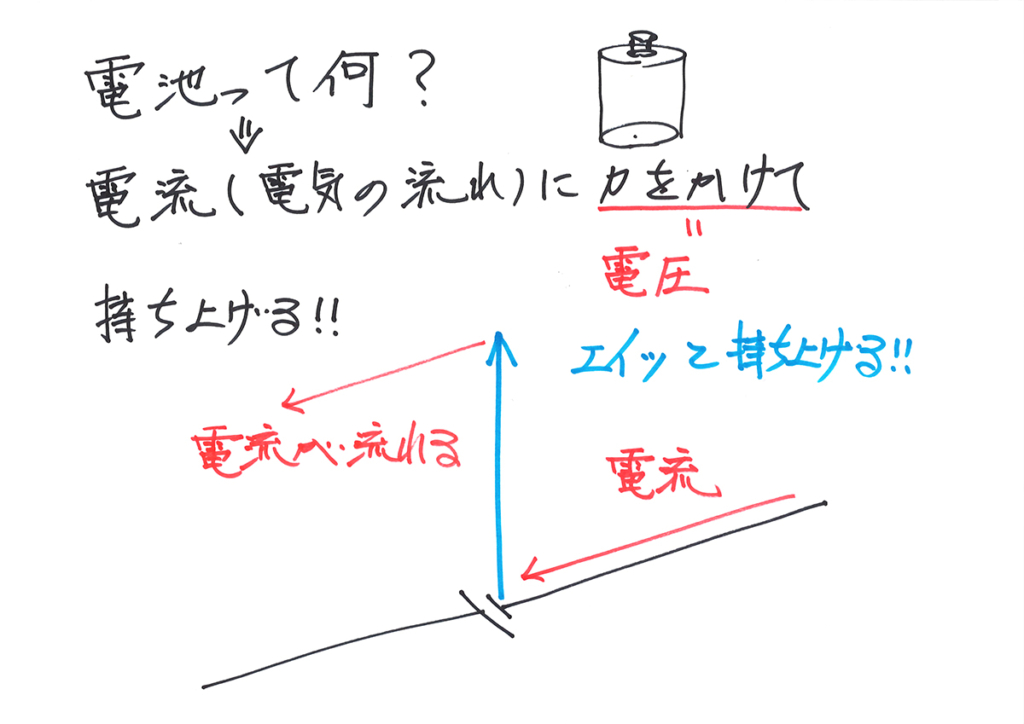




流れる電流を
持ち上げて、また流すよ!
・最初に電流をエイッと持ち上げて、電流を流す
・一周してきた電流を再度エイッと持ち上げて、電流を流す:持ち上げるエネルギーがある限り
直列つなぎのイメージ:便利な矢印


電池2個を直列につないだところ(電池)に、電流がやってきました。
これは、「最初に電流がなかった時」も同じです。
電池が1個でも何個でも、「電流がない回路に電流を持ち上げて流れを発生させる」のが電池です。



パワーがある限り、
何度でも電流を持ち上げるよ!
電池は「電流を持ち上げる」=「電圧をかける」イメージで考えましょう。
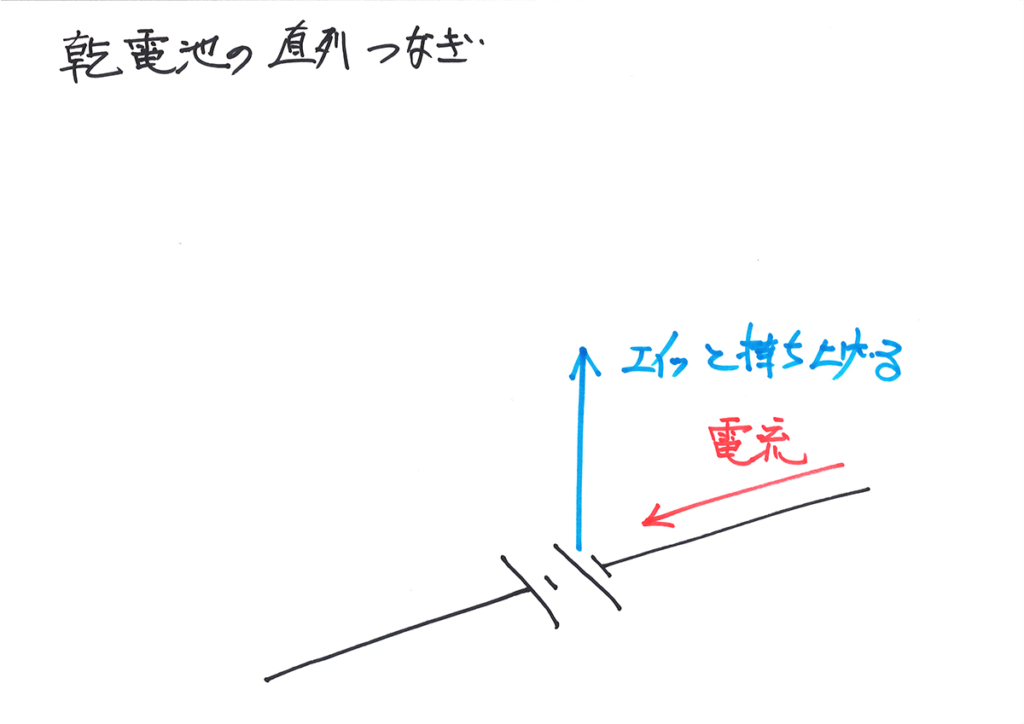

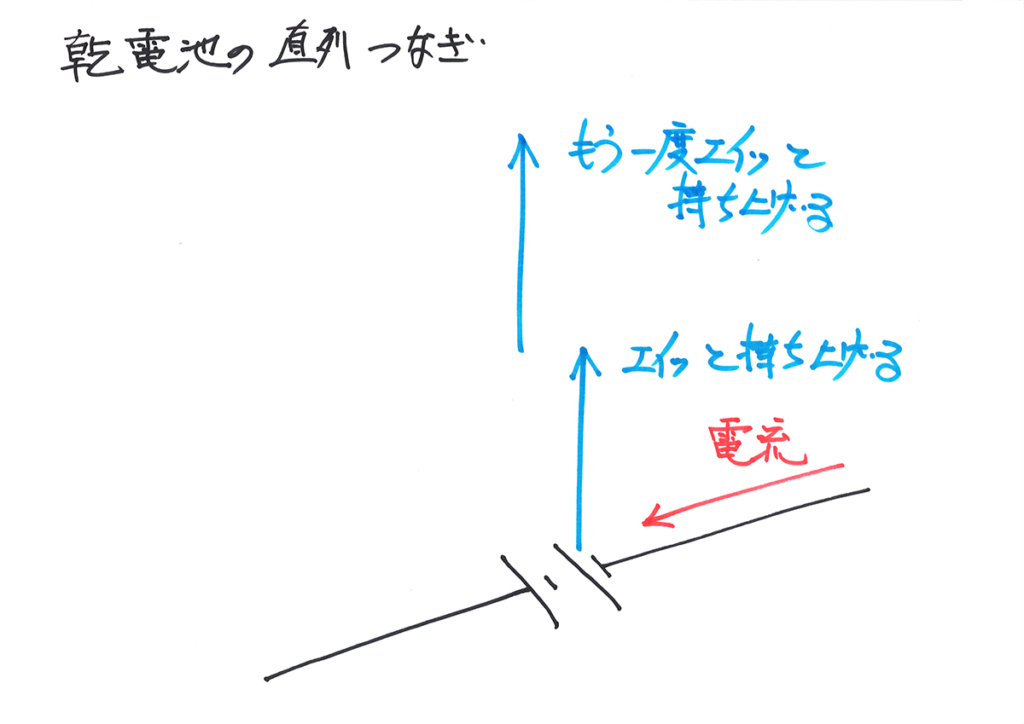
まず、一つ目の電池で、エイッと電流が持ち上がります。
「持ち上がる高さ=電圧」と考えたので、矢印で持ち上げる高さを表現して描きましょう。
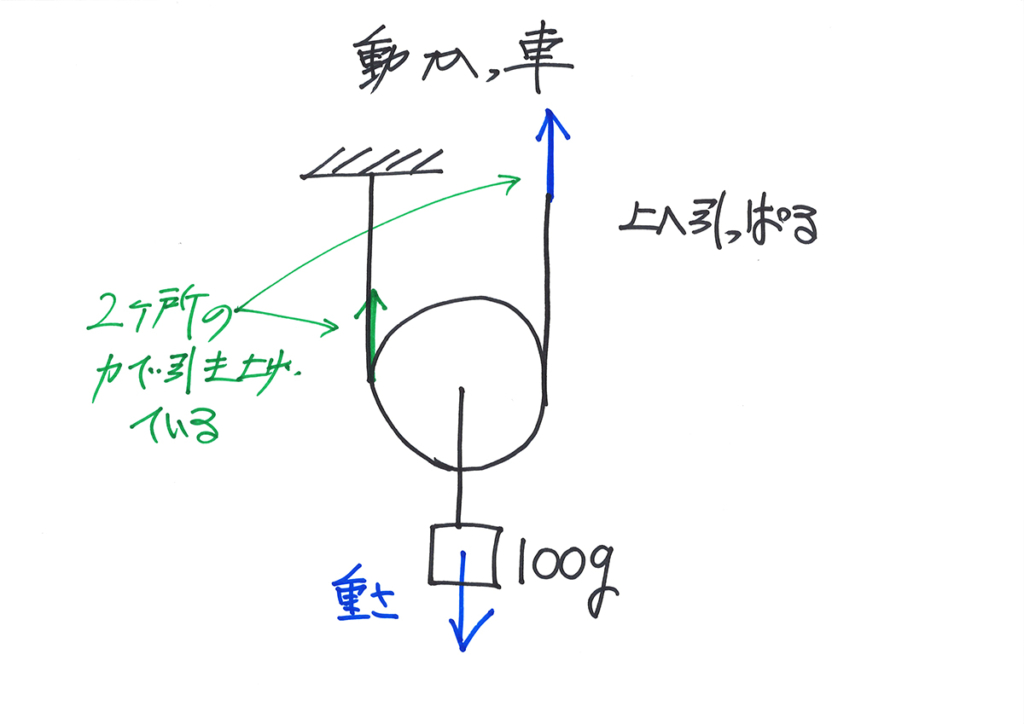

かっ車の時に、「ひも・糸を引っ張る力」と「おもりの重さ」を矢印で表す話をご紹介しました。
この時は、力の矢印に「向き」と「長さ」がありました。
・向き:力のかかる向き
・長さ:力の大きさ
電池が「エイッと電流が持ち上げる」高さを矢印で描いてみましょう。



ここでも
矢印を描くと分かるの?
電池一つで「エイッと電流が持ち上げる高さ=矢印一つ分」としましょう。
電池・電流は、「電池が持ち上げる高さは上向き」のイメージです。



上向きに電流が
持ち上がるんだね!
・長さ:電流を持ち上げる高さ(起電力)
力の時は「向き」と「長さ」がありましたが、今回は「向きは上向き」で変わるのは「長さ」だけです。



電池の電圧を考える時は、
向きは「全部上」だね!
力よりも「少し簡単」なので、こう考えてみましょう。
電流を持ち上げる高さ=矢印の数

流れている電流は、すぐに二つ目の電池に流れます。
算数の図形問題を解く際に、「矢印の話」を上記リンクでご紹介しました。
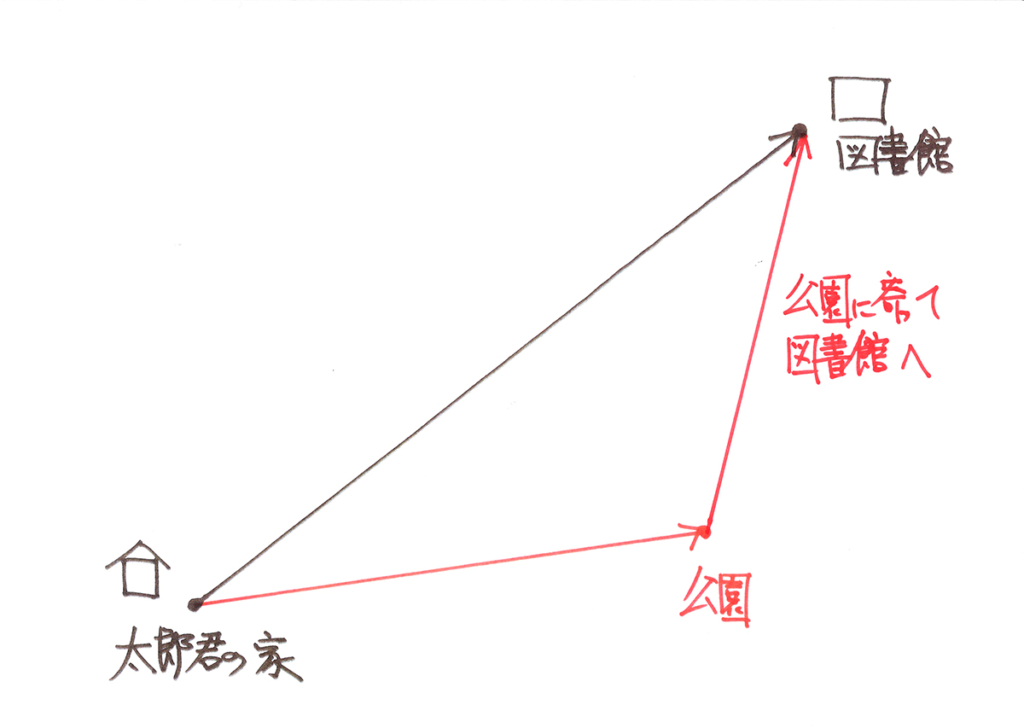

図形では、「矢印の向き」が大事です。
「向きと長さを考えて、つなぎ合わせる」と「矢印の和」になります。
二つ目の電池でもう一度、エイッと電流が持ち上がげます。
その時、「持ち上がる高さの合計」を考えてみましょう。
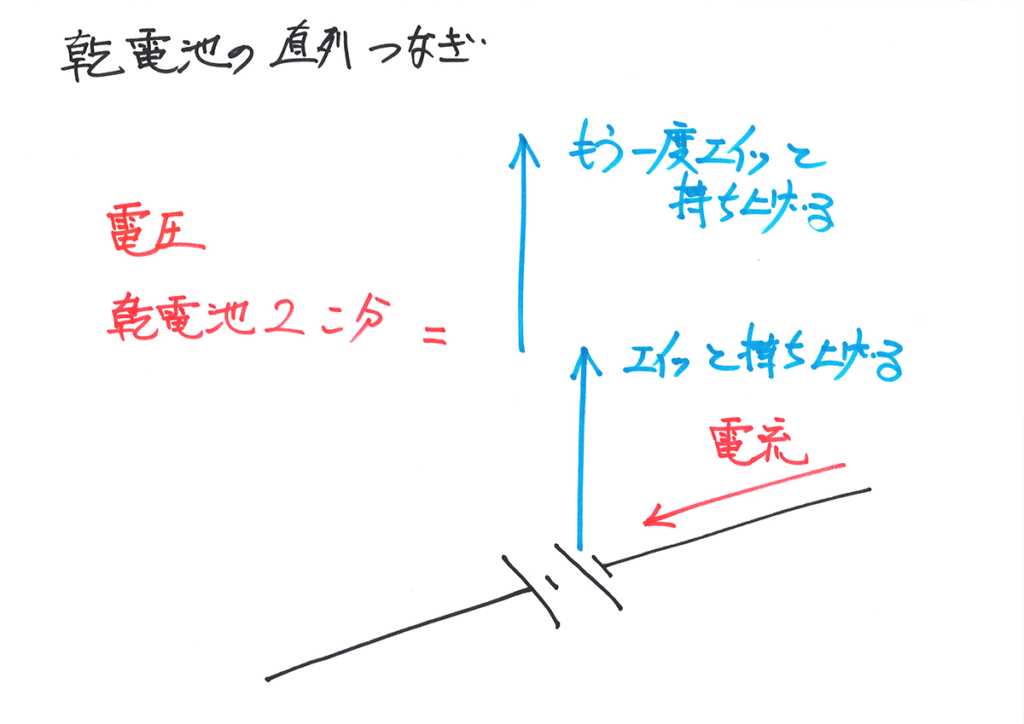




2回分
持ち上がるね!



電池2個分だから、
2倍の高さになるね!
矢印2回分持ち上がるので、「矢印2個分」持ち上がります。
そして、「矢印2個分の高さ=電池2個分の電圧」だけ、電流が持ち上がりました。
このように考えると、「電池が5個直列」の時はどうなりますか?



電流が、矢印5個分の高さ
持ち上がるね!



だから、電池5個分の
電圧だね!
同じように考えると「電池N個直列=電圧はN個分」が分かります。
・電流は、「電池の個数分の高さ=電圧」持ち上げられる
電池を持ち上げる向きは、「基本的に上」です。



電流を上に
持ち上げるよ!
電圧は「電流の流れを上向きに持ち上げる力」と考えましょう。
回路を一周している間に、電流はだんだん下がってしまいます。



そもそも、
電流はなぜ下がるの?
電流は見えないですが、回路を一周する間に電球や抵抗があります。
「抵抗」は文字通り「抵抗」なので、電流も疲れてしまうのです。
みなさんも、校庭でトラックを一周したら疲れると思います。



うん、
とても疲れる時があるね・・・
それと同じで、電流も抵抗にあうと疲れてしまい、高さが下がるのです。



やっと回路を
一周したけど・・・



抵抗もあったし疲れたから、
電圧が下がっちゃった・・・



また僕(電池)が
持ち上げてあげるよ!
そして、下がった電流は再び、電池によって「電圧の高さ」分持ち上げられるイメージです。
次回は、並列つなぎの話です。
次回は下記リンクです。