前回は「図形問題を得意になるコツ〜図形の対称性・正三角形の対称性と特徴・対称性から分かる大事なこと・動点Pの動きと対称性・問題10(4)解法A〜」の話でした。
問題10(4)再掲載

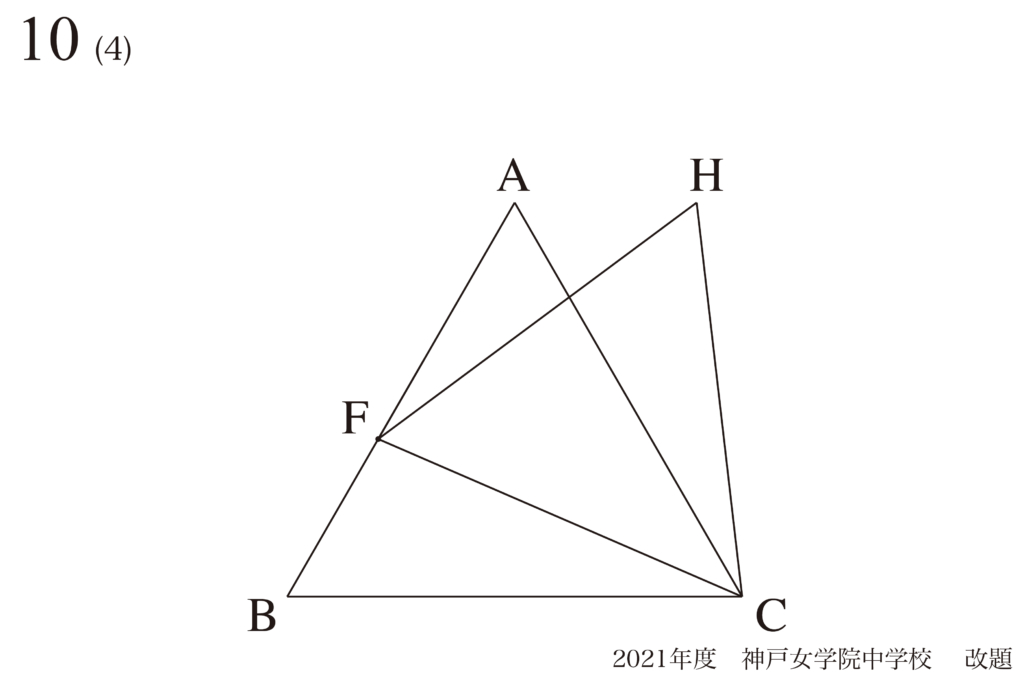
動点Pの攻略法:動く点の行動範囲と対称性
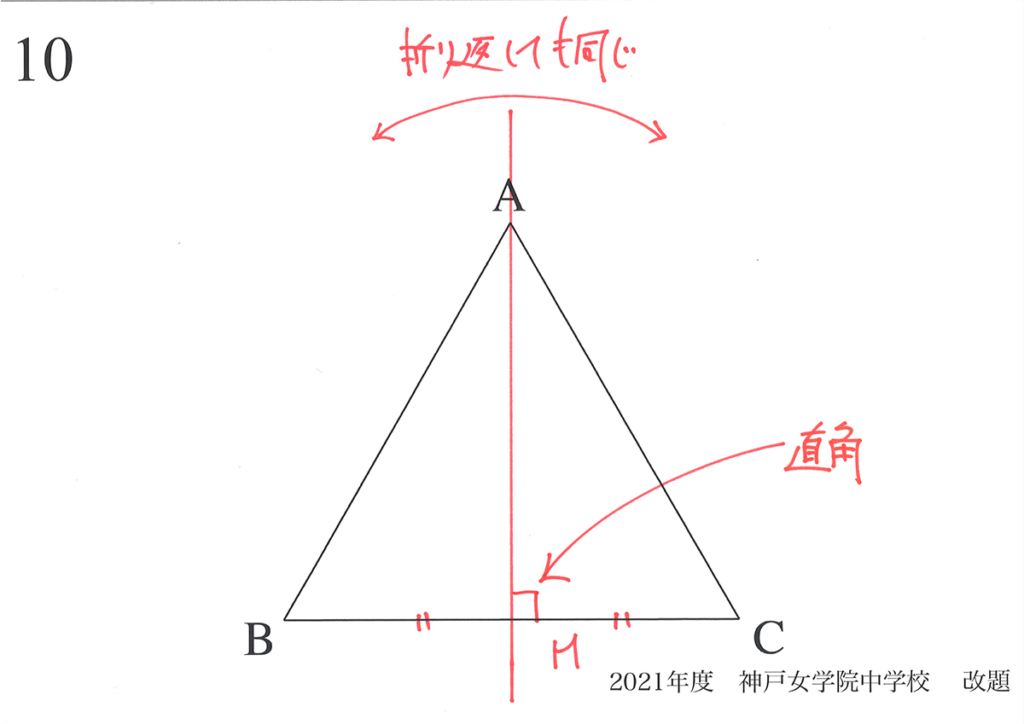
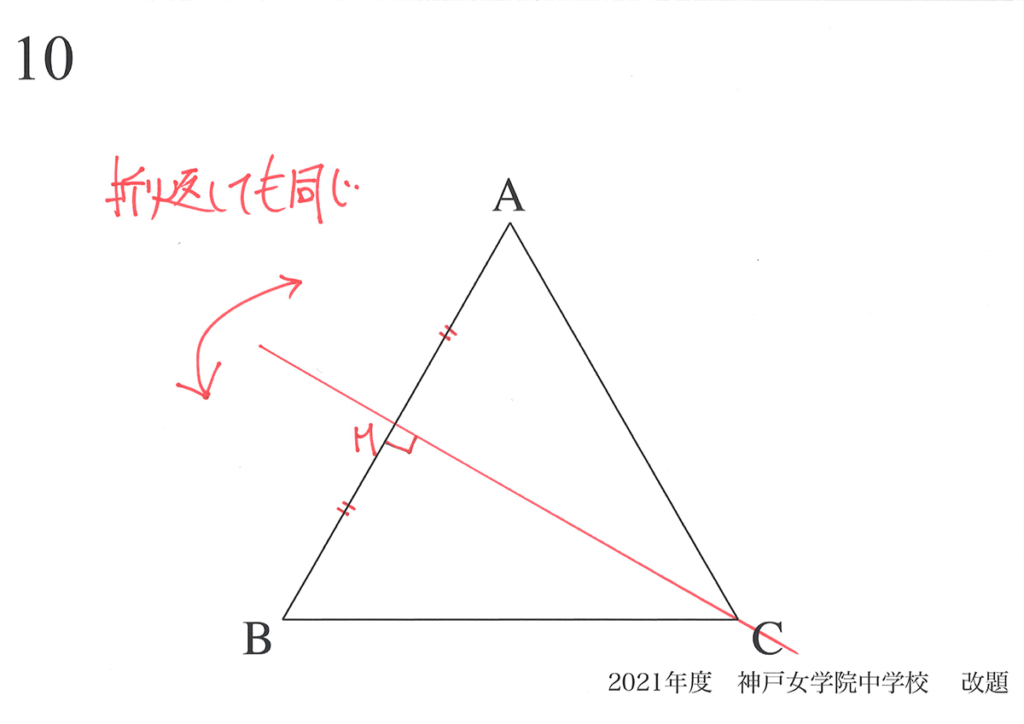
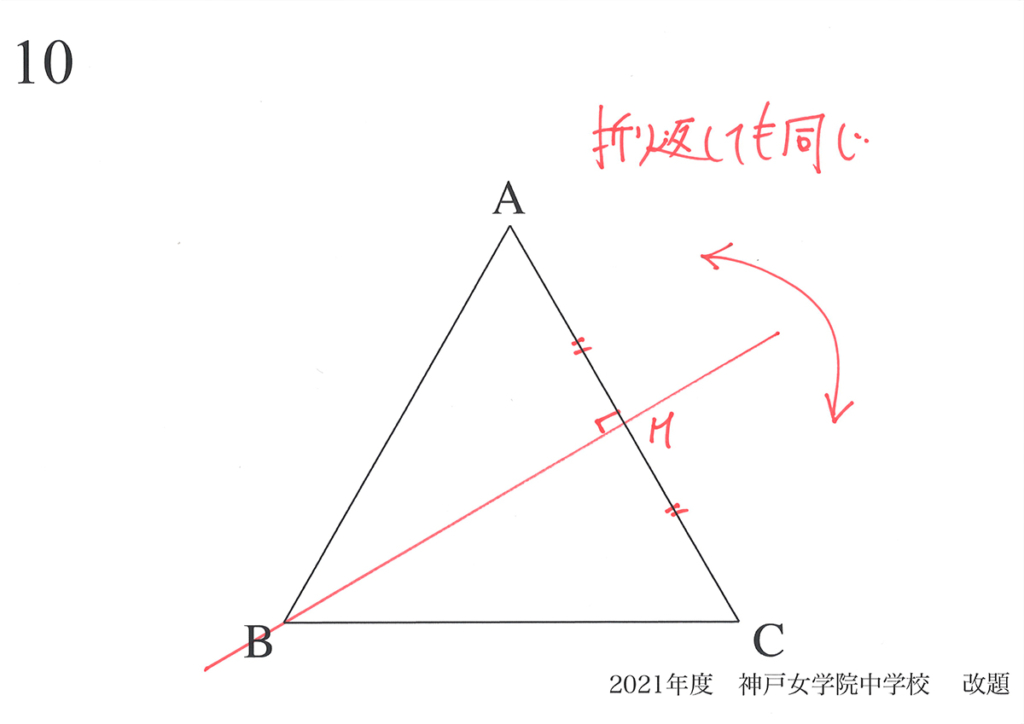
前回は「正三角形の対称性」を考えました。
・ある線で折り返すと、きれいに折り返せる(折り返したら同じ)
・対称性のある図形には、様々な特徴(辺の長さが等しい、角度が等しい)がある
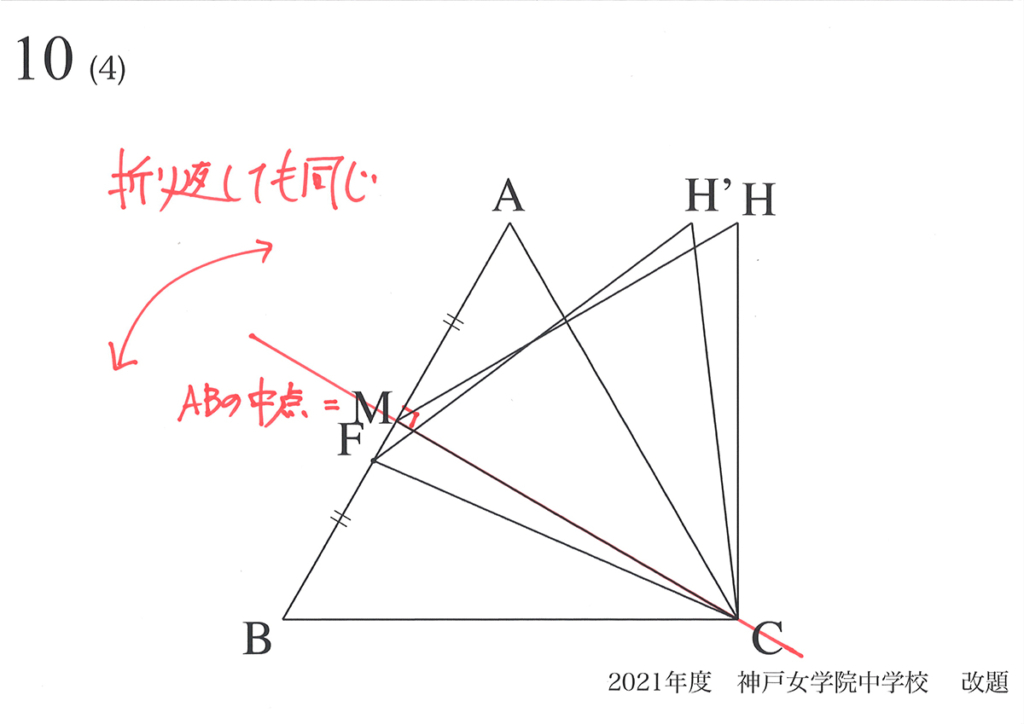
「対称性を考える」から、中線CMを軸として、動点Fが「Mの前後で同じ」とわかります。
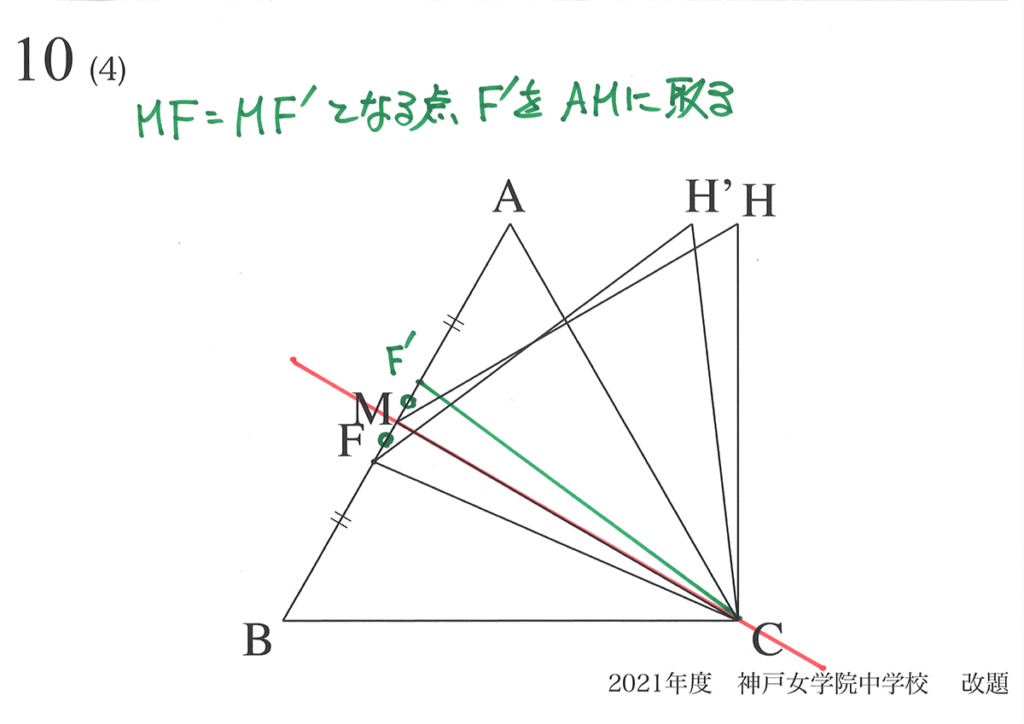
感覚的に分かるかもしれませんが、きちんと考えてみましょう。
中線CMを軸と考えて、その両側の同じ位置にFとF’を考えましょう。
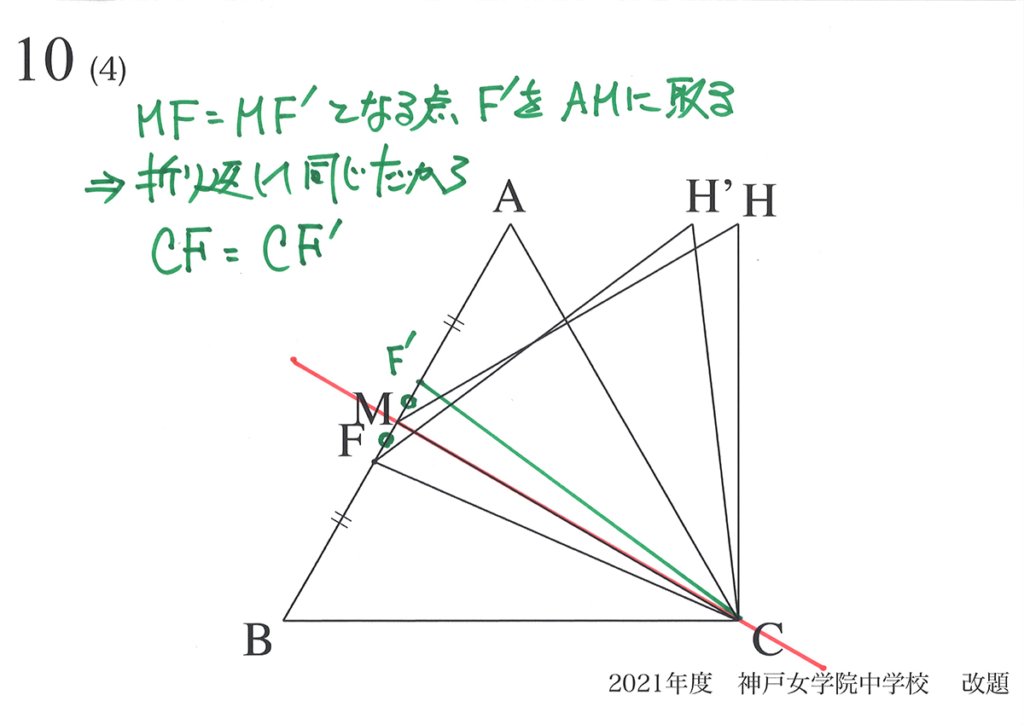
「折り返して同じ」ですから、CF=CF’ となります。
そこで、点Fが頂点Bから頂点Cヘ移動してゆく過程を考えてみましょう。
 男子小学生
男子小学生「BM上にある時と、AM上にある時」が
同じだね!
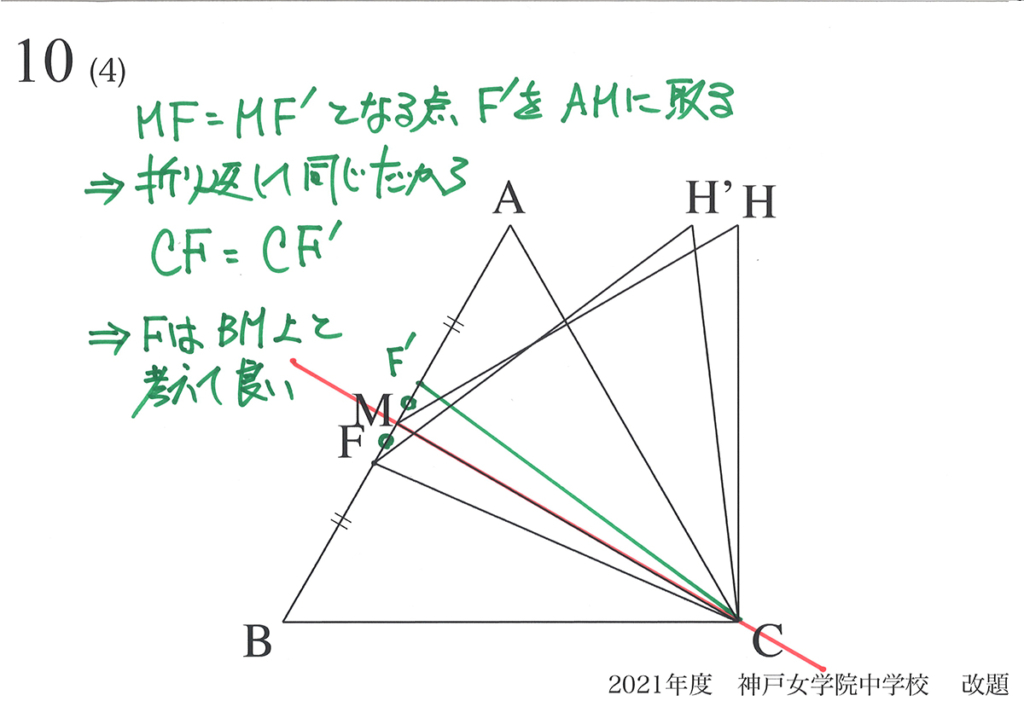

「同じ」なのですから、動点Fが「BM上にある」時を考えれば良いのです。
これで、動点Fの動く範囲・行動範囲が半分に絞れました。
このように、「動く点の範囲を限定する」ことは非常に本質的で大事なことです。
面積が最小となる時:直角三角形の基本性質
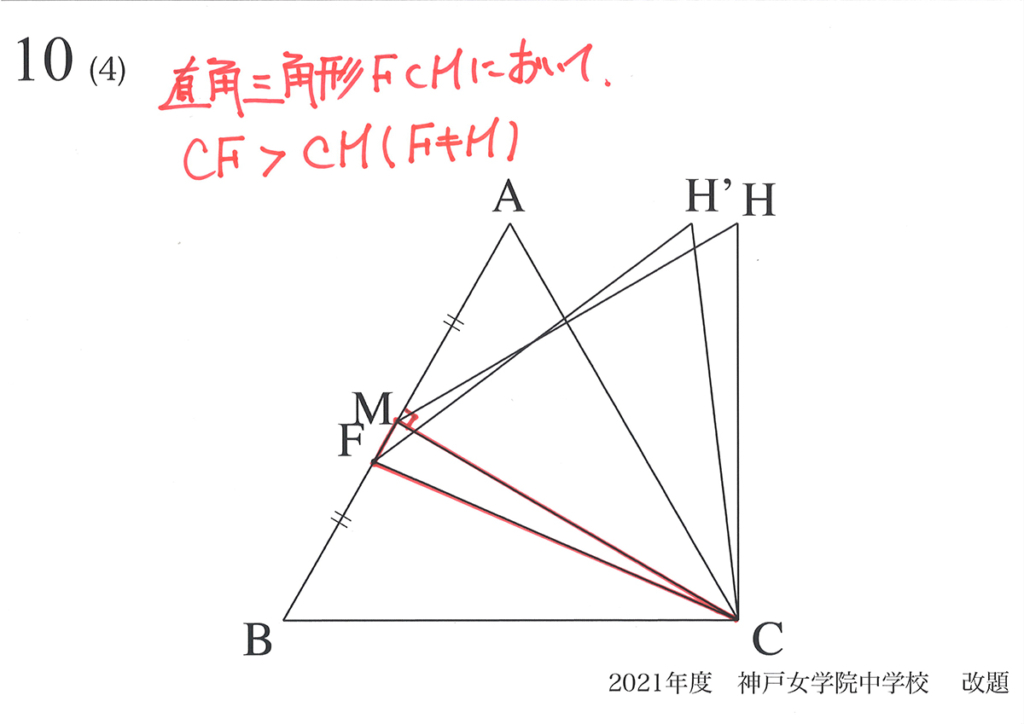

ここで、「相似形の面積比=(辺の比)x(辺の比)」を思い出しましょう。
「面積が最小になる」のは、正三角形FCHの「辺の長さが最小になる」時です。
直角三角形において、「斜辺は必ず他の辺の長さより長い」です。
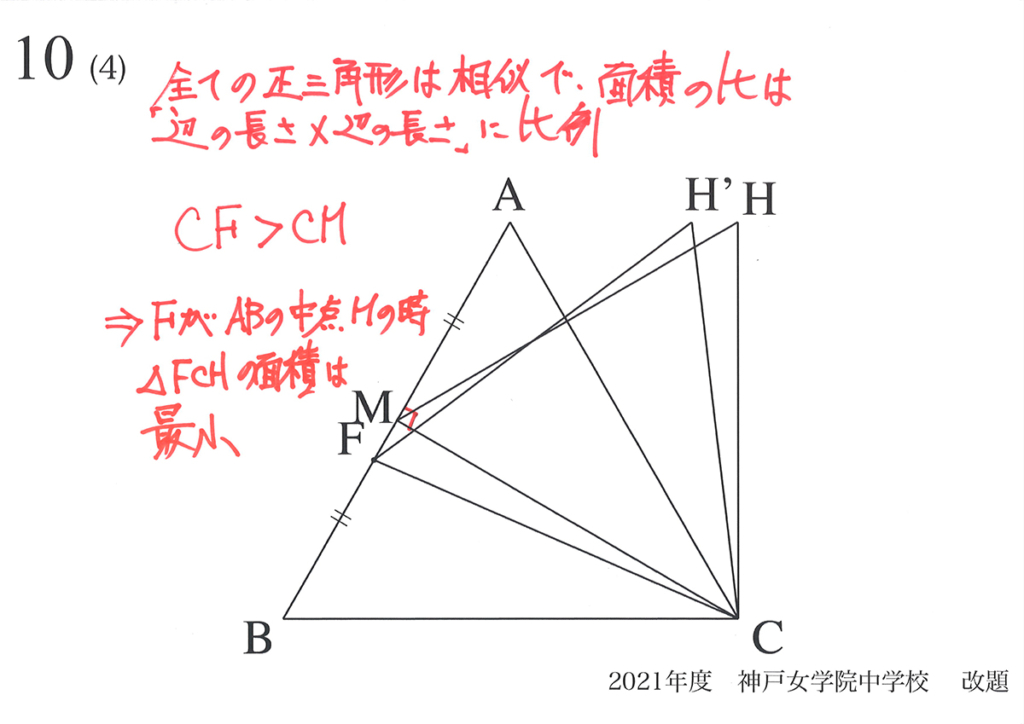

上記の通り「動点Fが辺ABの中点Mにある時に、正三角形FCHの面積が最小」とわかりました。
今回、辺ABの中点Mを考えて「角CMB=角CMA=直角」が非常に大事でした。
図形において、直角が出てきたら直角(二等辺)三角形が隠れています。
図形問題で、大事なことは「平行・対称・直角」です。
・平行と対称に注目
・直角がある時は、隠れている直角三角形、直角二等辺三角形に着目
変化しないモノに注目する考え方
この問題は、このように考えるのが最もシンプルです。
もう一つ、考え方があります。
少し遠回りですが、図形問題で大事な「変化しない量・モノ」に着目する考え方です。
近々、ご紹介しますので、考えてみて下さい。
次回は下記リンクです。


