前回は「公式を暗記ではなく理解して学力アップ〜相似形の面積比・図形のイメージ・方眼紙と図形・問題10(4)ポイント〜」の話でした。
問題10(4)再掲載

面積比を描いて理解:方眼紙のイメージ
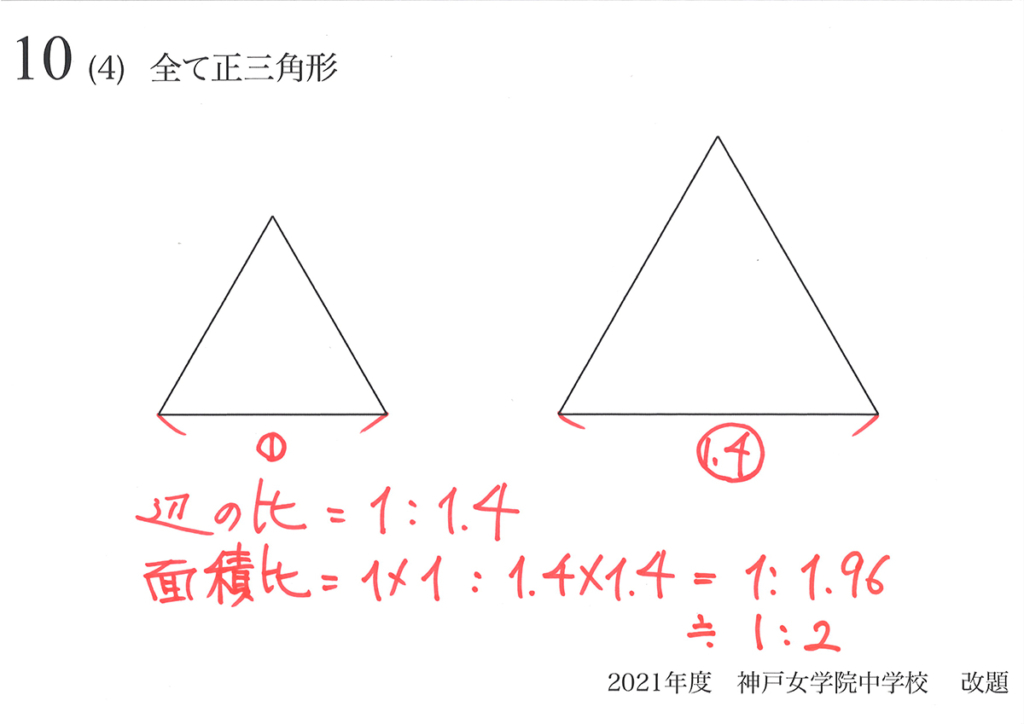
今回は、面積比の公式を考えて、しっかり理解しましょう。
上の二つの正三角形は「辺の長さは40%しか違わないのに、面積は約2倍になる」のです。
「相似形の面積比=(辺の比)x(辺の比)」が「なぜなのか?」を考えます。
例えば、相似比が 1: 3 の場合は、辺の長さが3倍になります。
全体的に、3倍になるので「面としては3×3=9倍に広がる」雰囲気を感じてください。
 男子小学生
男子小学生雰囲気で
良いの?
・面積や比など「求める対象」を具体的に考えてゆく論理性
・図形の大きさや長さをイメージする力


正三角形を方眼紙に描くことを考えてみましょう。
出来れば、方眼紙かグラフ用紙などに実際に描くと良いでしょう。
相似比が3ということは「辺の比が3倍」になるので、正三角形がグーっと広がってゆくイメージです。
元の正三角形が「一マス(1cmx1cm)」を基準とすることを考えます。



すると、相似比3の正三角形は広がった「一マス(3cmx3cm)」が
基準になる感じだね!
このように図形が「大きくなるイメージ」をつかみましょう。
「何かの理由」をしっかり説明できることが大事ですが、「なんとなく」の雰囲気も大事です。
面積比を計算して理解
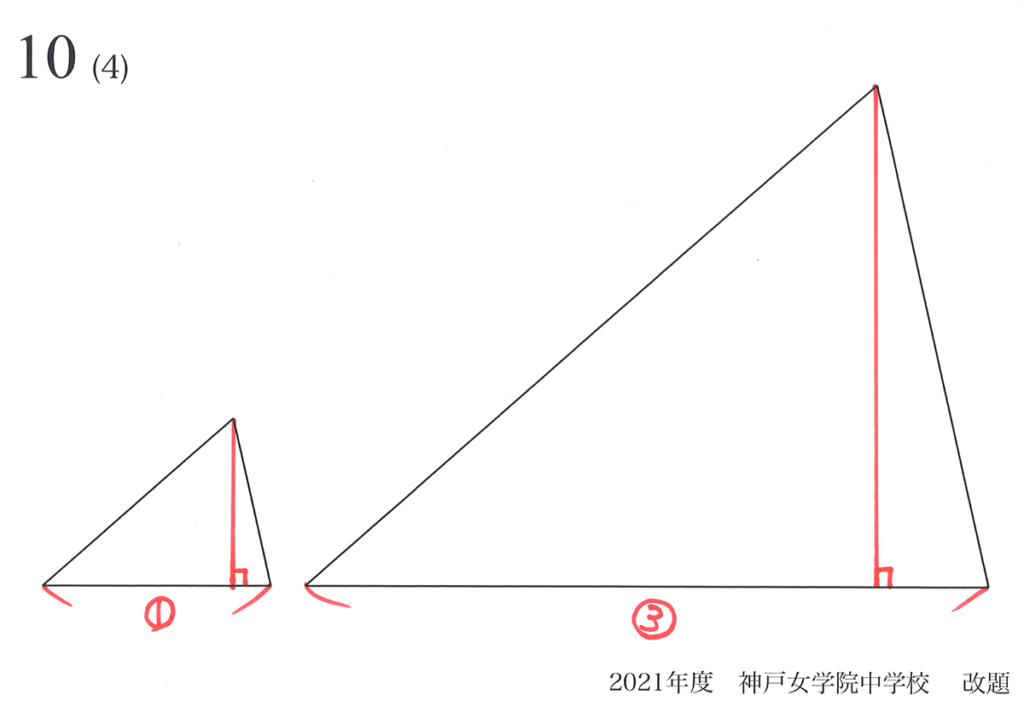

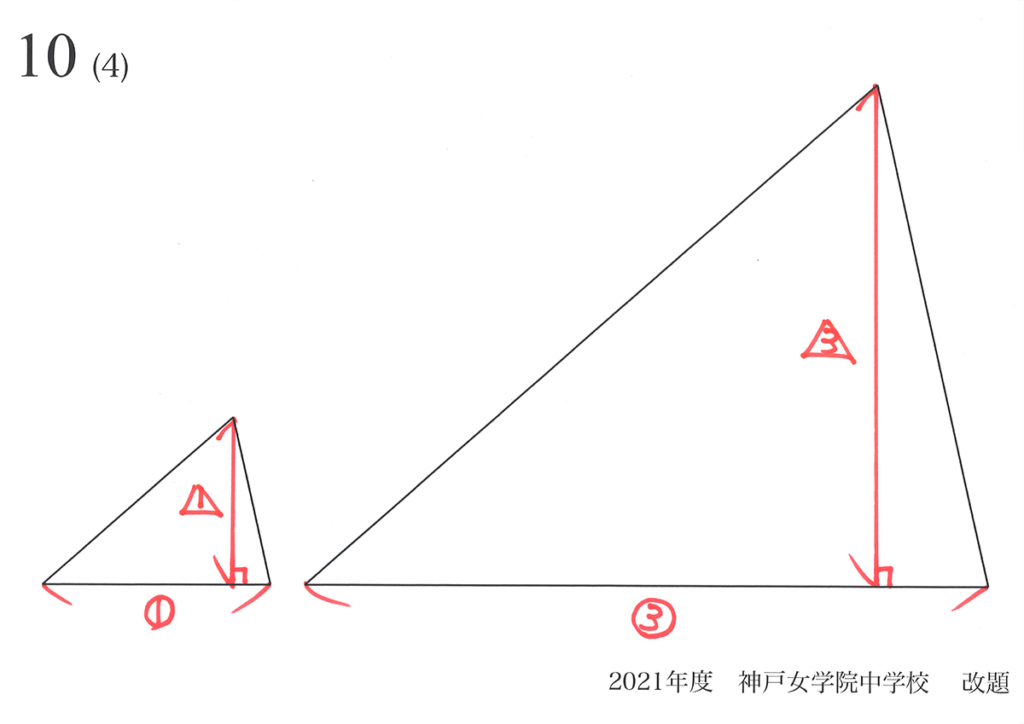
きちんと説明するなら、三角形の面積を考えるために、垂線を引いてみましょう。
これらの「垂線の長さの比」を考えてみます。




垂線の長さの比も
一緒だね!
相似形ですから、垂線の長さも1 : 3 になります。
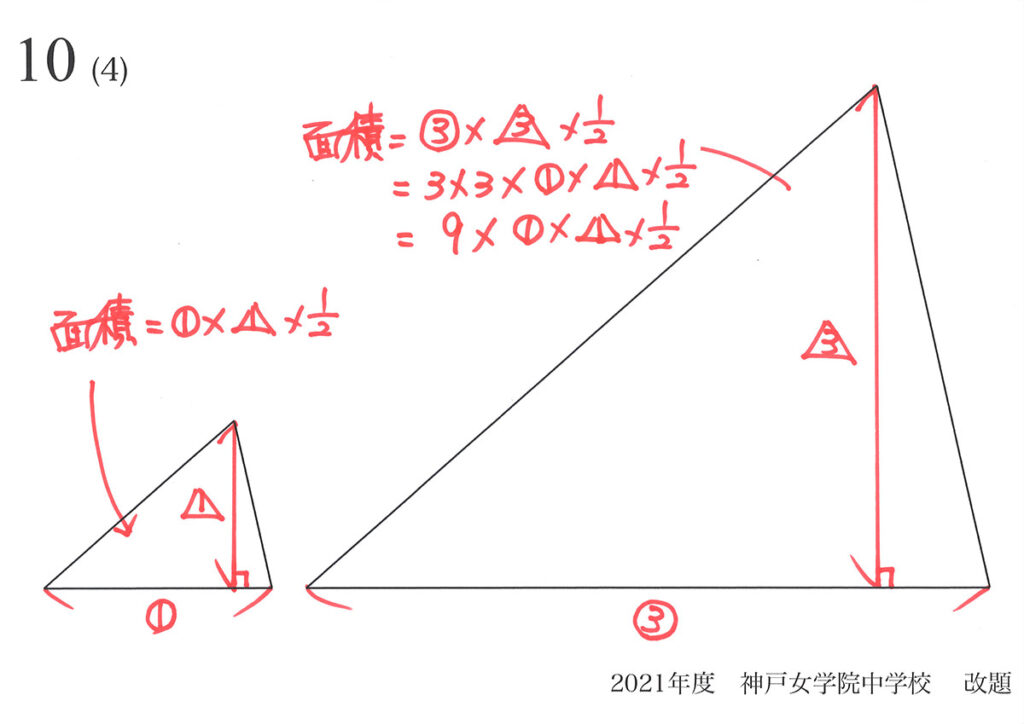

そうすると、面積は上のように計算できます。
これで、三角形の場合は「相似形の面積比=(辺の比)x(辺の比)」が、はっきり分かりました。
四角形の相似形の面積比:大きい対象は小さく分割
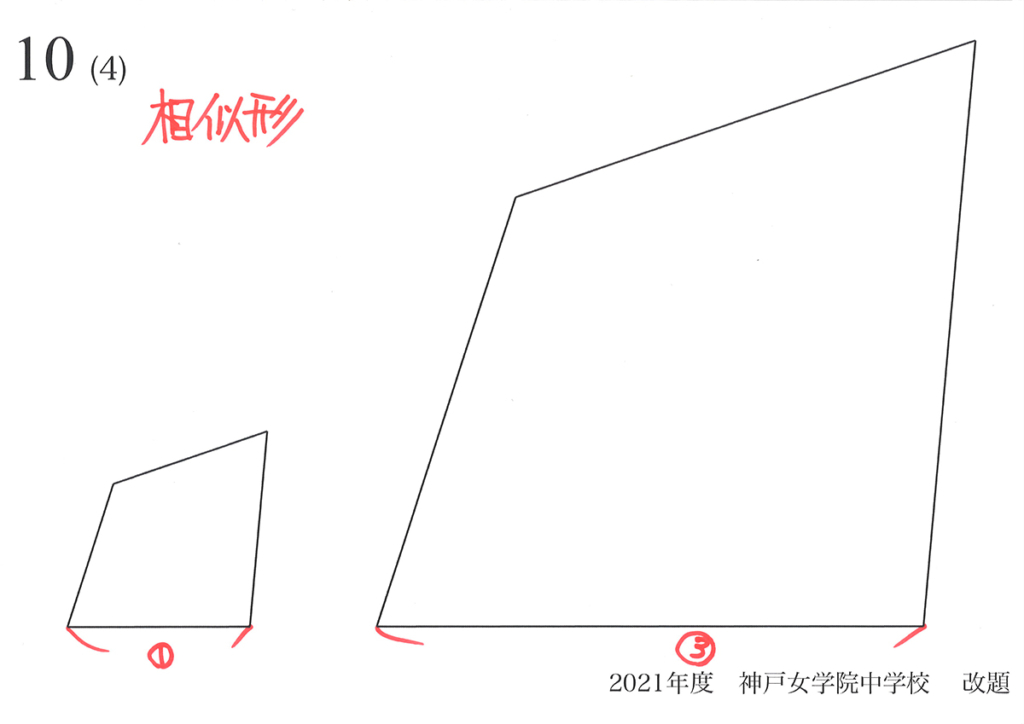

四角形の場合はどうなるか考えてみましょう。
これも方眼紙の「辺の比に応じて、面が広がってゆく」イメージが大事です。
すると、同様に「相似形の面積比=(辺の比)x(辺の比)」と分かります。



確かに平面図形なら、三角形でも四角形でも
同じように「基準のマス」が広がるんだね。



四角形も三角形の時と同じように
相似形の面積比=(辺の比)x(辺の比)は知っていたけど・・・



方眼紙を考えると、
そんな感じがする!
しっかり考えてみましょう。
少し歪な四角形同士が相似形で、辺の比=1 : 3 です。
直感的には「同じはず」ですが、きちんと説明できますか?



う〜ん、
そうだね・・・



きちんと説明するのは、
三角形の時より難しそう・・・
少し考えてみましょう。
大きくなったら、分割してみましょう。
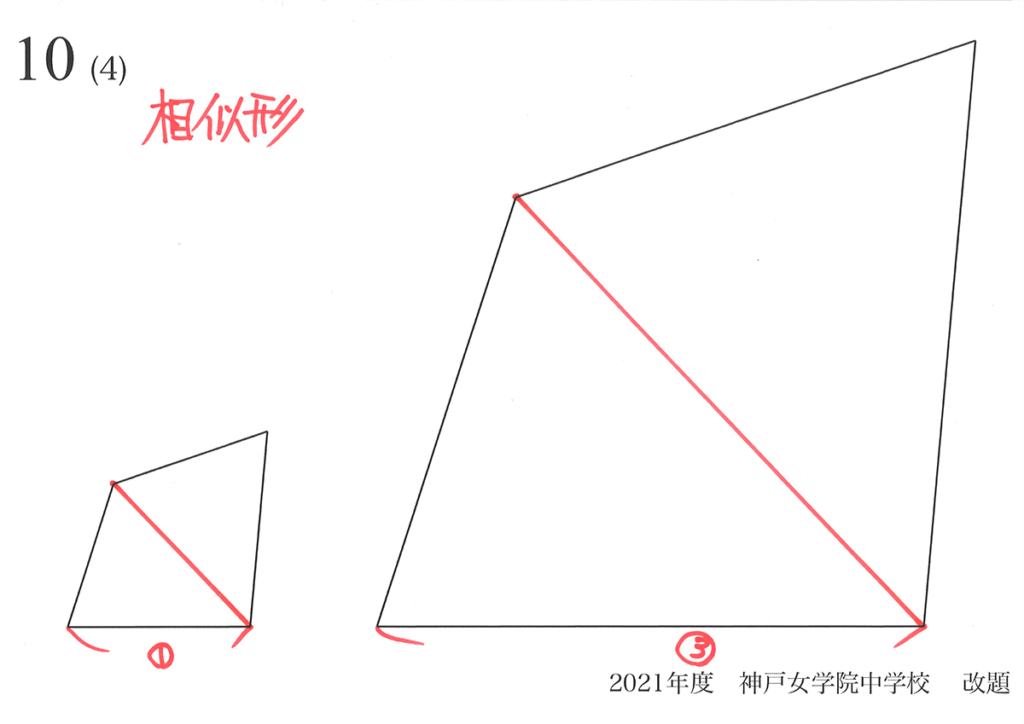

二つの三角形に分けました。
こうなると、先ほどの三角形の場合と一緒です。
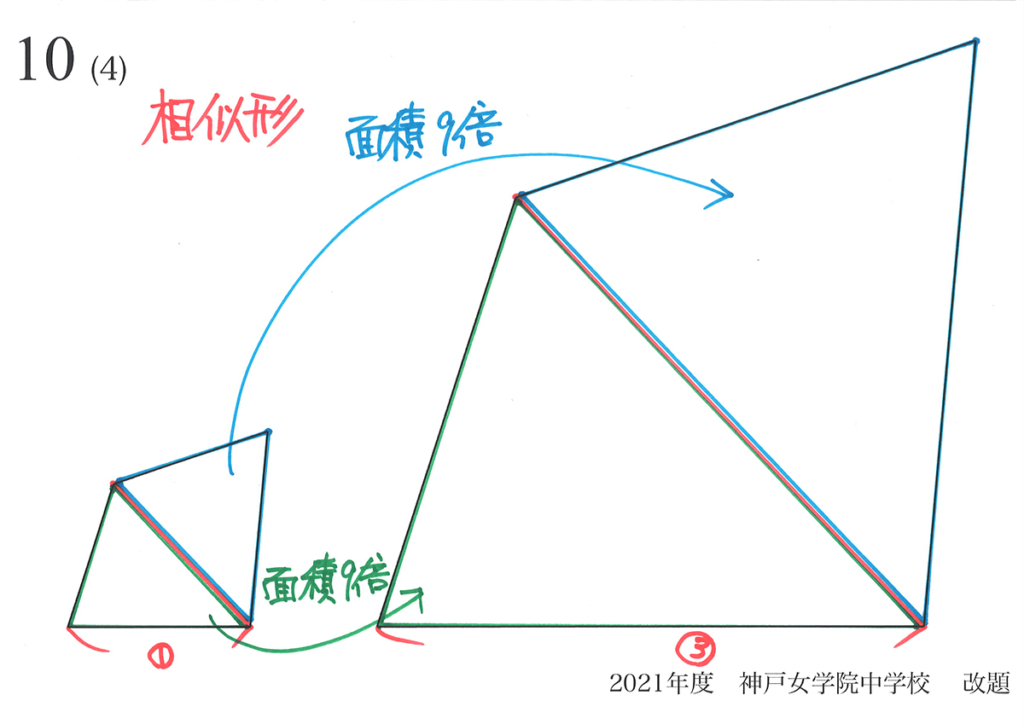

それぞれの三角形の面積比が1 : 9 となります。
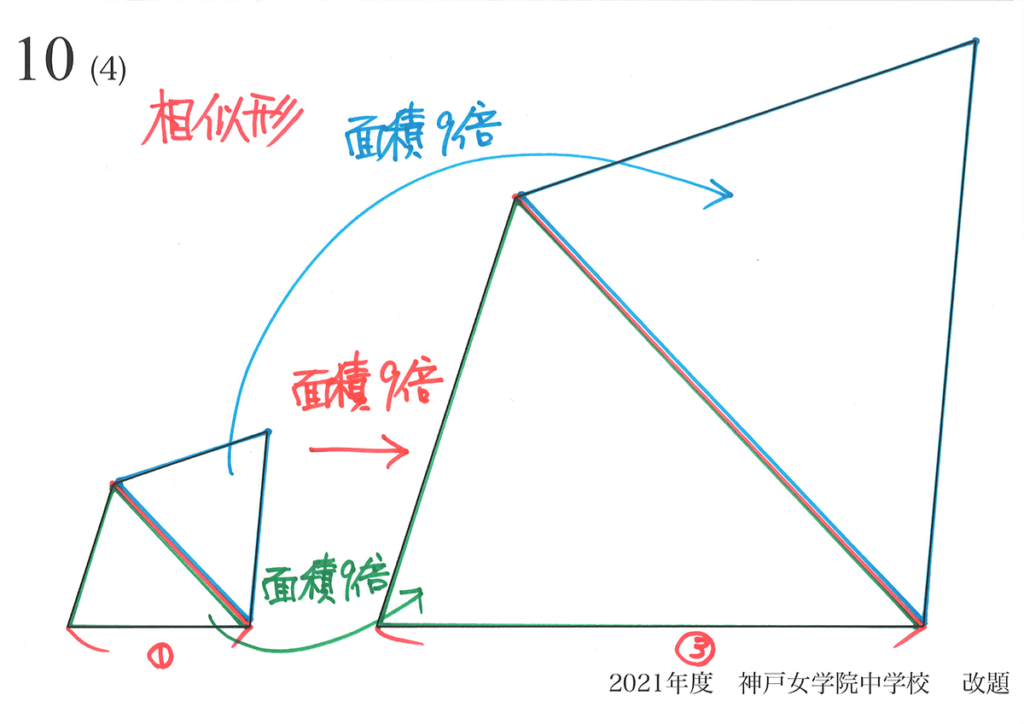

すると「それぞれの三角形を足しても面積比=1 : 9」になります。



四角形を三角形に分割したら、
分かりやすい!
小さく分割する考え方:階段を上がるイメージ
こうして考えると、五角形でも六角形でも「三角形に分割」すれば、同じように面積比が考えられます。



確かに
そうだね!



分けると
分かりやすいね!
「小さく分ける」ことは非常に本質的なことで、分かりやすくなります。



確かに、
小さい方が分かりやすい。
分けてみると対象が小さくなって、考えやすくなります。
日常にある階段も「小さく分割する」の考え方で、作られています。
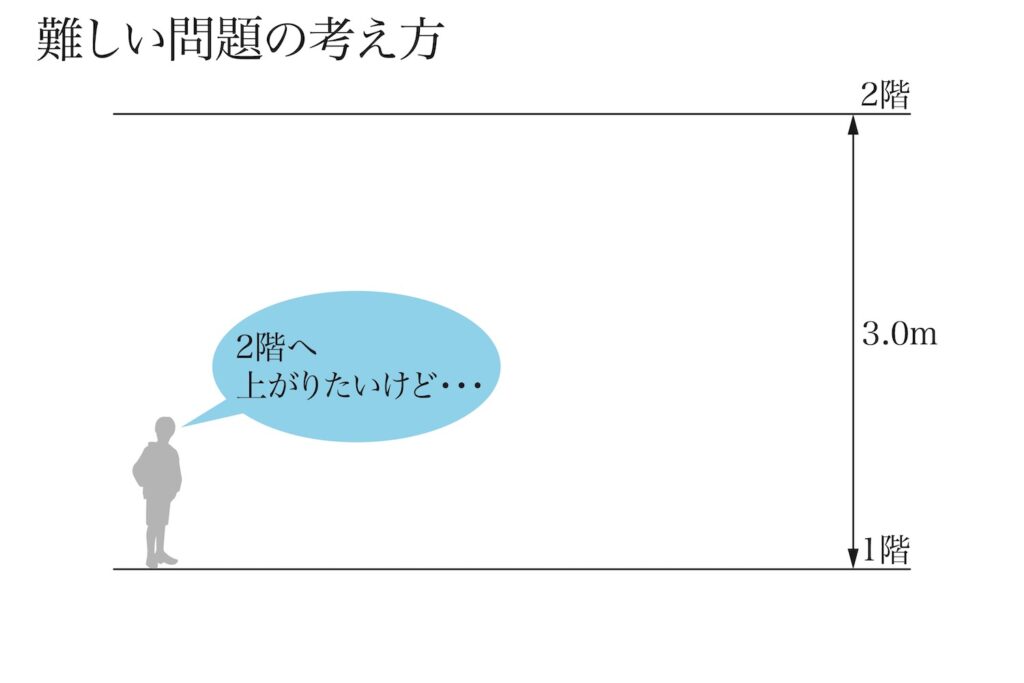

「一階から二階に一気に上がることは出来ない」です。
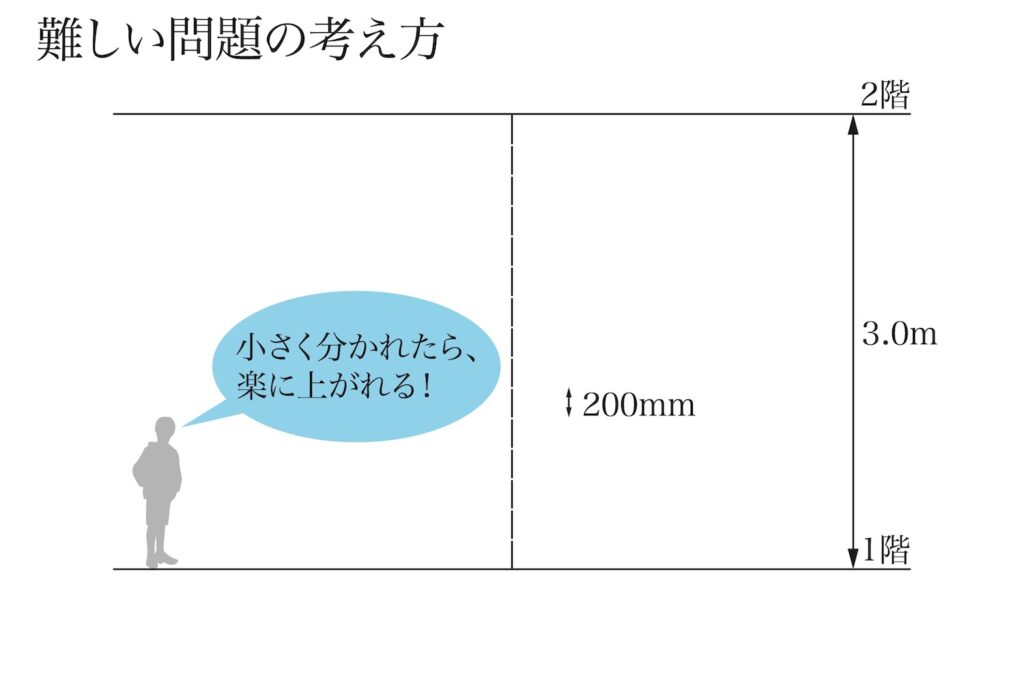

そこで、階段の段ごとに「高さを分割」します。
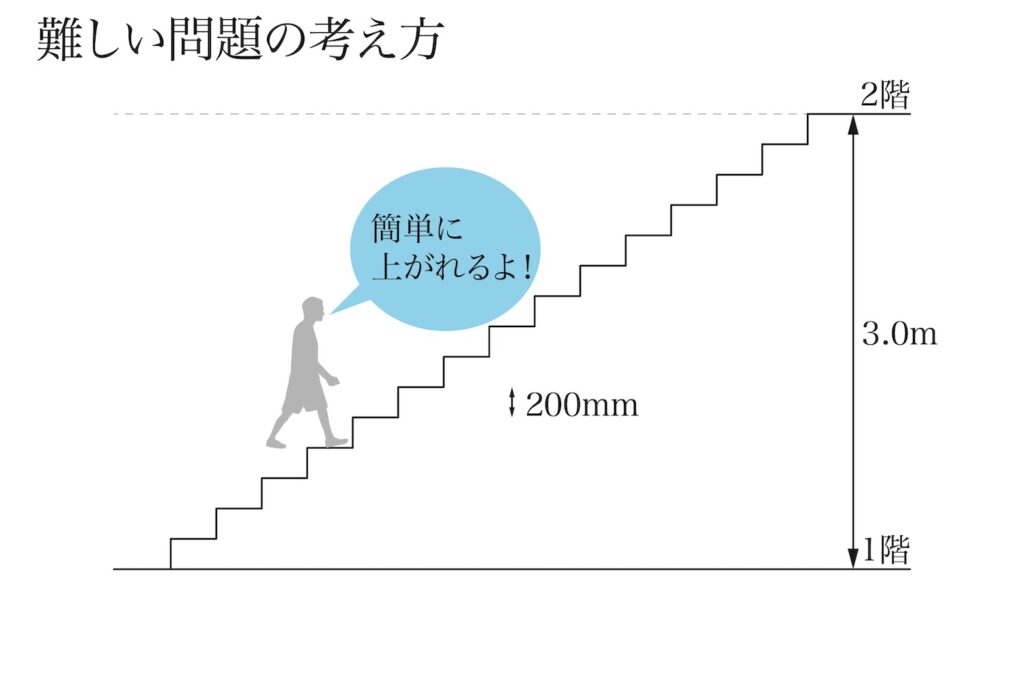

一気には上がれませんが、少しずつなら「上がれる」ようになります。
少しずつ学んで学力を上げる話を、上記リンクでご紹介しています。
図形に限らず、文章題でも「分けてみたらどうかな?」と考えることが大事です。
すると、解く鍵が見つかる可能性があります。
・大きい対象を小さくすると分かりやすくなる
・小さくすると「見えてくる大事な性質」がある
図形でも文章題でも「対象を小さくする・分ける・分割する」ことを考えてみると良いでしょう。
次回は下記リンクです。



