前回は「図形問題の解き方・ポイント・コツ 2〜図形の補助線と「きれいに分割」・辺の比と面積比・図形全体を描いてみること=全体像を見ること・手を動かして脳を活性化+イメージ膨らませる〜」の話でした。
図形問題の解き方・ポイント・コツ：一番良い解き方とは？
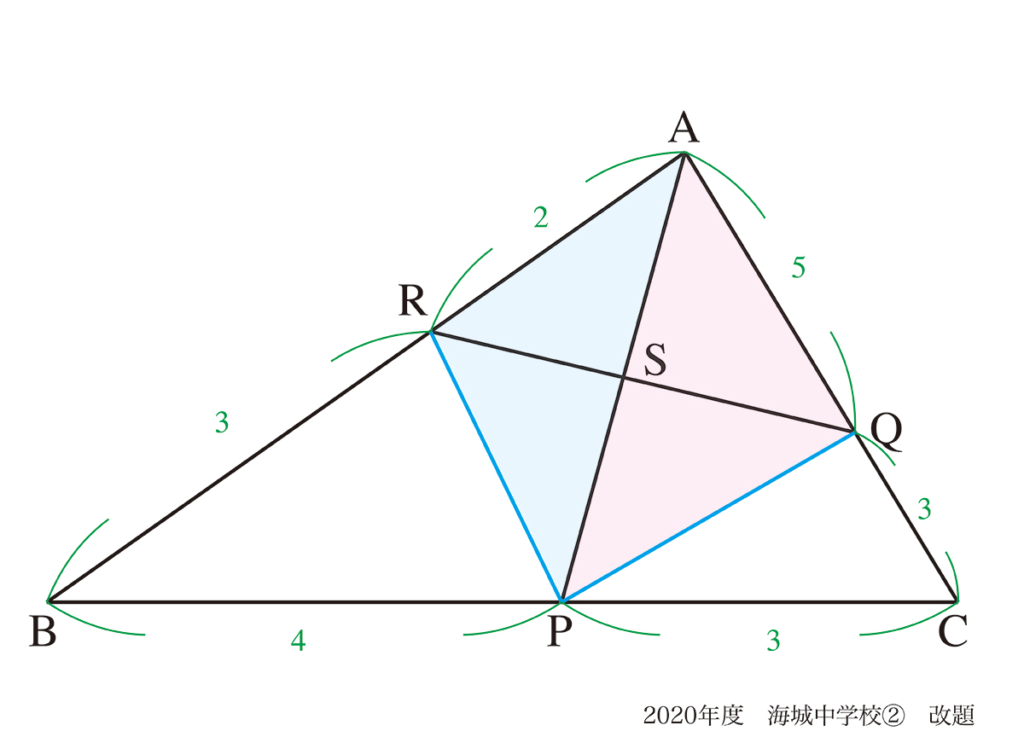
前回は、図形問題に対して「何に着目するか」の話をしました。
算数・数学においては、「何に着目するか」は問題を解く際の最も大事なポイントです。
この問題は、「面積比に着目」と「辺の比に着目」の二通りの考え方をご紹介しました。（上記リンク）
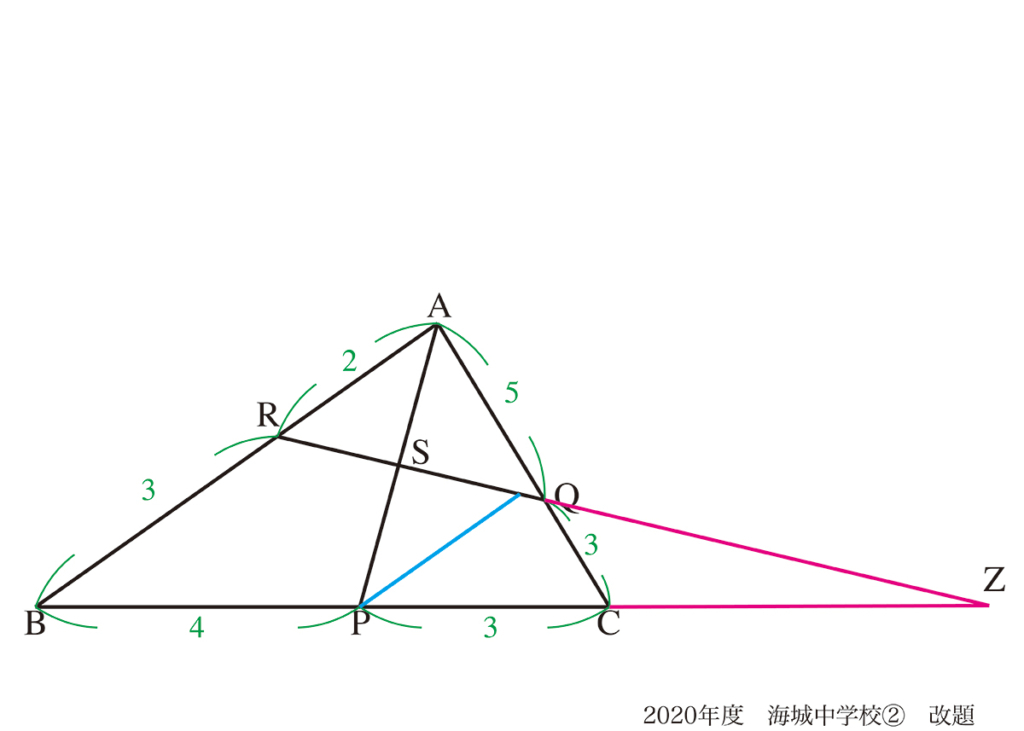
「辺の比」に着目した場合、「図形の外」に飛び出して補助線を引きました。（上記リンク）
「面積比」と「辺の比」の、どちらに着目しても解けます。
「辺の比」に着目して解くことが、比較的多い図形問題。
「辺の比を考えて、面積比を求める」ことは沢山あります。
対して、「面積比を考えて、辺の比を求める」のは、比較的少数派かもしれません。
男子小学生確かに、面積比を
考えて問題解くのは少ないかも・・・
「何に着目するか」で、問題に対する考え方は、だいぶ変わってきます。
男子小学生うん・・・
全然違うね・・・
「辺の比」に着目して解く場合も、「補助線の引き方」はいくつか考えられる場合があります。
男子小学生ということは、
解き方が沢山ある場合があるんだね。
女子小学生「一番良い解き方」が出来るように
なるには、どうしたらいいの？
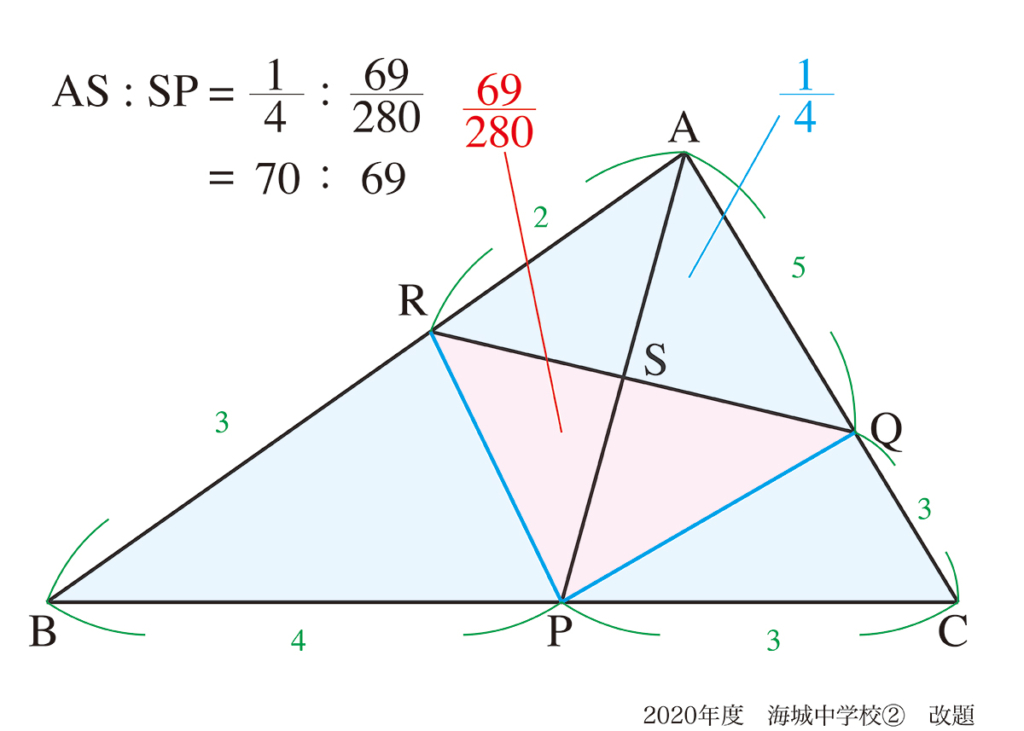
この問題では、「面積比に着目」した方が「スッキリ解ける」感じがあります。
なぜ「スッキリ解ける」のかというと、二本の補助線によって、図形がきれいに分けられたからです。
・図形の中に補助線を1,2本引いて、三角形・四角形にきれいに分割する
・きれいに分割できたら、それぞれの面積を辺の比から考える
・面積比から、求めたい辺の比を求める
男子小学生じゃ、面積比を
考えたようが「良い解き方」なのかな？
女子小学生ただ、補助線が二本
必要なのが、難しいかも？
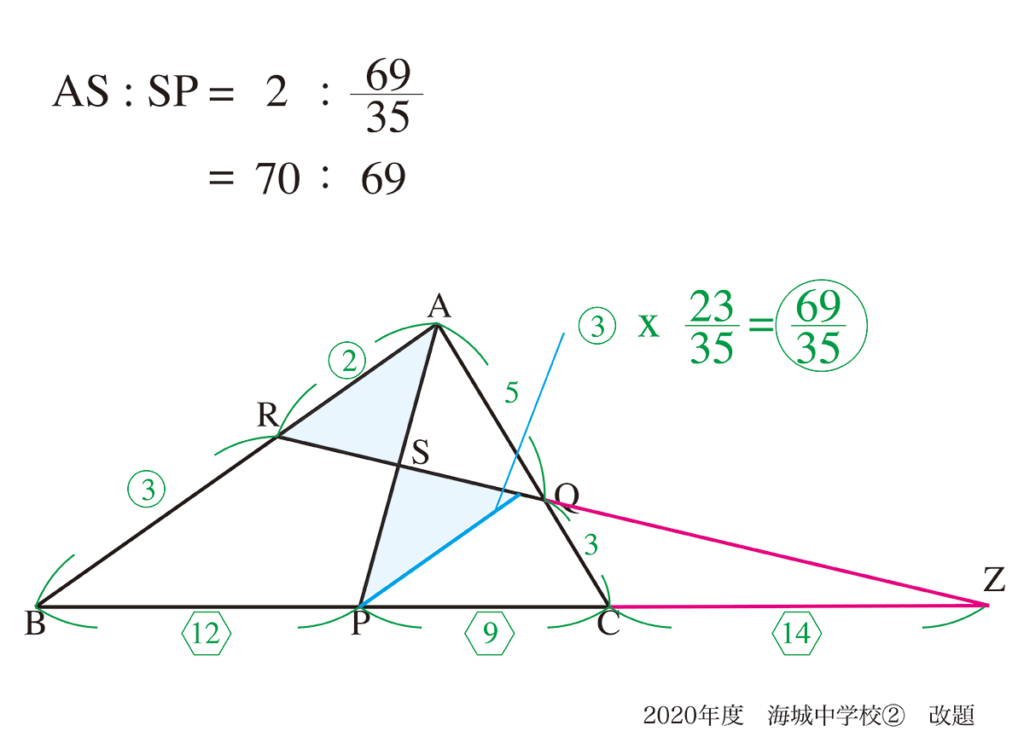
男子小学生でもさ、「図形の外」に出て
辺の比を考える場合は・・・
男子小学生補助線の本数が増えて、
三本になるね・・・
女子小学生外側は二本だけど、
「考え方」としては一本に近いかもね・・・
「補助線の本数少ない」方が「簡単に感じる」かもしれません。
男子小学生それは、そうだよ・・・
本数が一本違う、だいぶ違うよ・・・
「二本と三本」または「一本と二本」と考えると、「多い方が難しい」と感じられるかもしれません。
面積比・辺の比を考えたときに「補助線を描く」方針に共通点はありませんか。
男子小学生面積比は、三角形に分割する
ように、二本補助線引いてるね。
女子小学生辺の比は、図形の外に
三角形を作るために、二本補助線を引いているね。
つまり、どちらの考え方でも、「何に着目し、何を作るために補助線を引くか」がポイントです。
男子小学生なるほど！
そう考えると、補助線が二本でも難しくないかも。
女子小学生補助線の数は、問題の難しさとは
関係ないかも・・・
・面積比、辺の比など「何に着目するか」を考える
・「何を作るために補助線を引くか」を考える
・多くの場合、補助線によって、新たに（相似）三角形が生まれる
上の問題は、「面積比」の方が「早く解ける」ので、
塾講師こういう問題のパターンは、
こっちの解法が思いつくように！
このように「パターン」で習う場合も、あるかもしれません。
試験においては、「早く解ける」ことは大事です。
一方で、「自分に合う解き方をしっかり習得する」姿勢も大事です。
男子小学生結局、どっちの解法が
「良い解法」なの？
「良い解法」は、それぞれの方の考え方・個性によることがあります。
「自分に合う解き方」で、出来るだけ解くように、日頃から学んでゆきましょう。
仮に、その方法が「少し時間がかかる」としても、慣れると短時間で出来るようになるでしょう。
「図形を回転」など視点を変える考え方
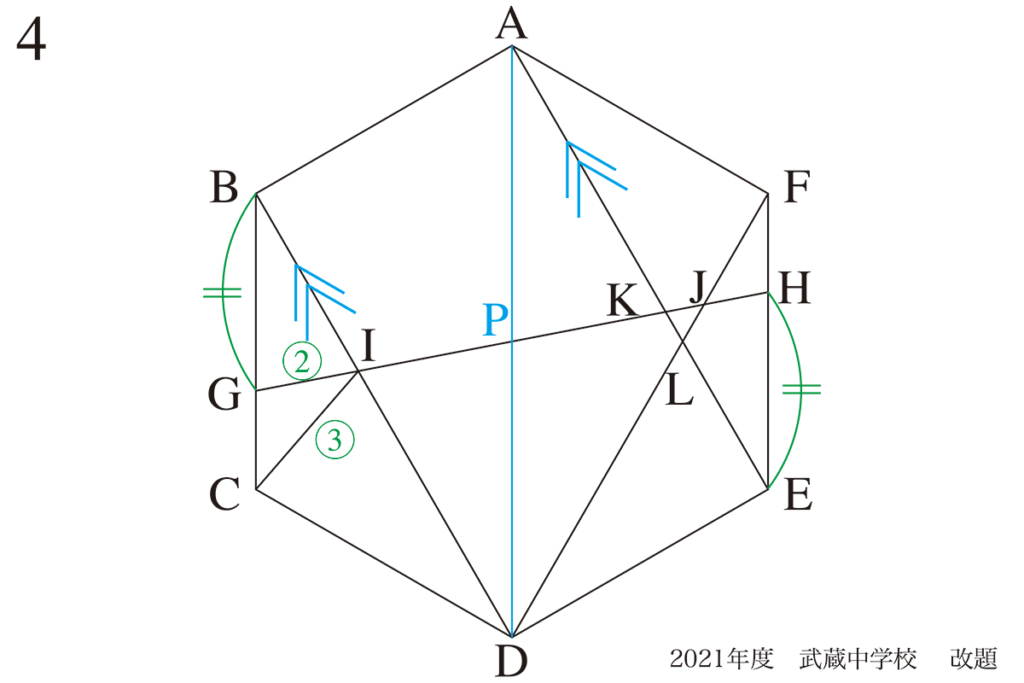
今回は「視点を変えてみる」話です。
問題4解法Bの話を、紹介しました。（上記リンク）
ここで、平行な二本の直線に気づくことの大事さをご説明しました。
これは、正六角形のことをよく理解している方なら、すぐに気づくかもしれません。
男子小学生言われたら分かったけど、
パッとは思いつかなかった・・・
女子小学生「線が平行」は、
二つの線が「水平」か「垂直」ならすぐ分かるけど・・・
女子小学生この図形みたいに、
斜めだと、気づかないかも・・・
「斜めで分かりにくい」と感じるときは、自分の都合の良いように視点を変えましょう。
この場合、「斜めだから気付きにくい」ので、「斜めが垂直になるように」回転しましょう。
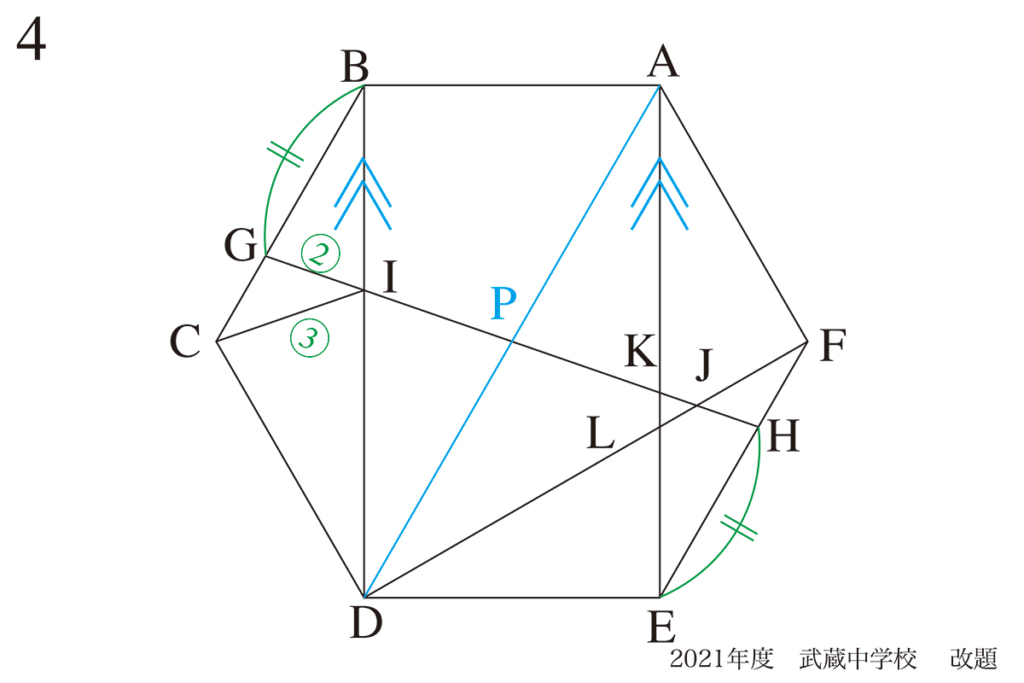
正六角形の中心Pを中心に30°回転してみましょう。
男子小学生これだったら、
すぐに平行って分かるよ！
女子小学生この形だったら、
分かりやすい！
ちょっと回転するだけで、一気に見やすくなります。
自分で回転した図形を描いてみたり、イメージしてみることはとても大事です。
問題文の図形全体を描いてみると、図形の大事な性質が分かるようになります。
図形の大事な性質は、参考書等で「言葉で色々とまとめられている」より、実感しましょう。
・自分で図形（全体）を描いて、性質を実感
・言葉だけで学ぶよりも、一度手を動かして理解すると忘れない
そして、このように「回転してみる」「視点を変えてみる」考え方に至りやすくなります。
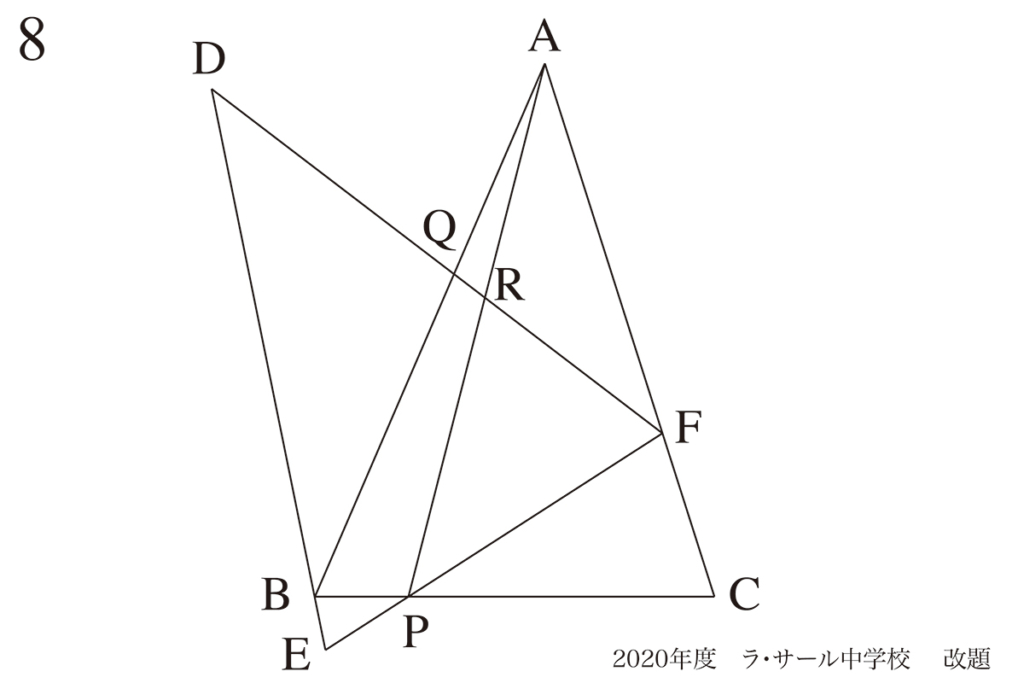
問題8(1)(2)の解法の話をご紹介しました。
図形の回転では「同じ角度・長さ」に着目しましょう。
・同じ角度、同じ長さを探す
・「同じ図形」を回転しているので、同じ角度がたくさん見つかる
・「同じ角度」から相似形を見つけて、相似比・辺の比を考える
図形問題で「小問がたくさんある時」は、問題文の図形が複雑になる傾向があります。（上記リンク）
それらに関する直線・点などが全て描かれている場合があるからです。
この問題では、(1)(2)にはAPは本質的に無関係で、なくても良い線です。
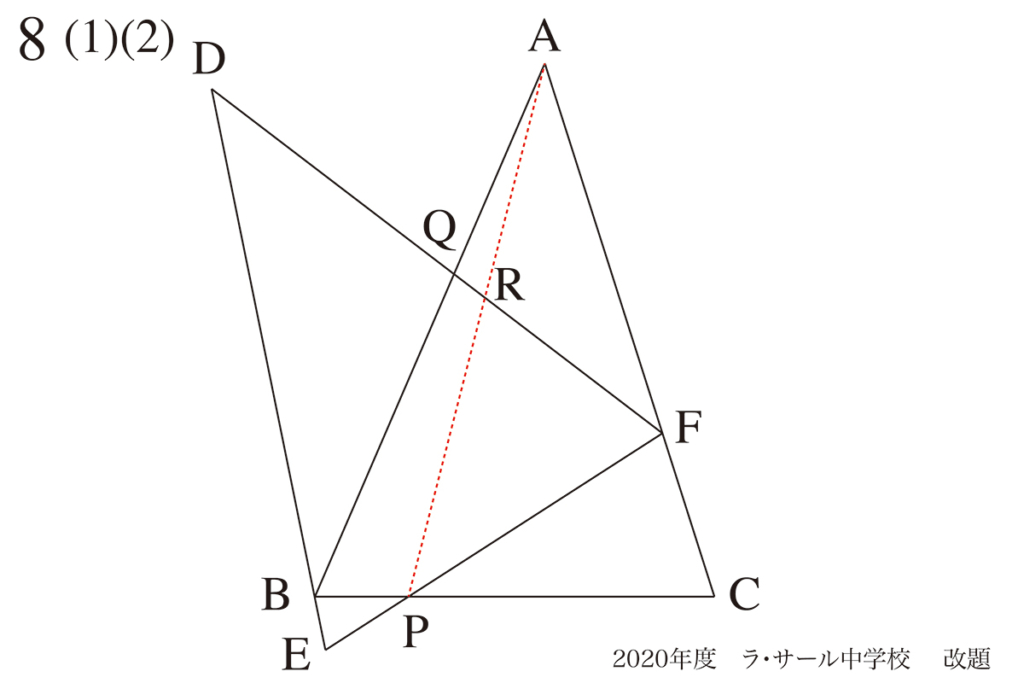
ですから、APは消してしまいましょう。
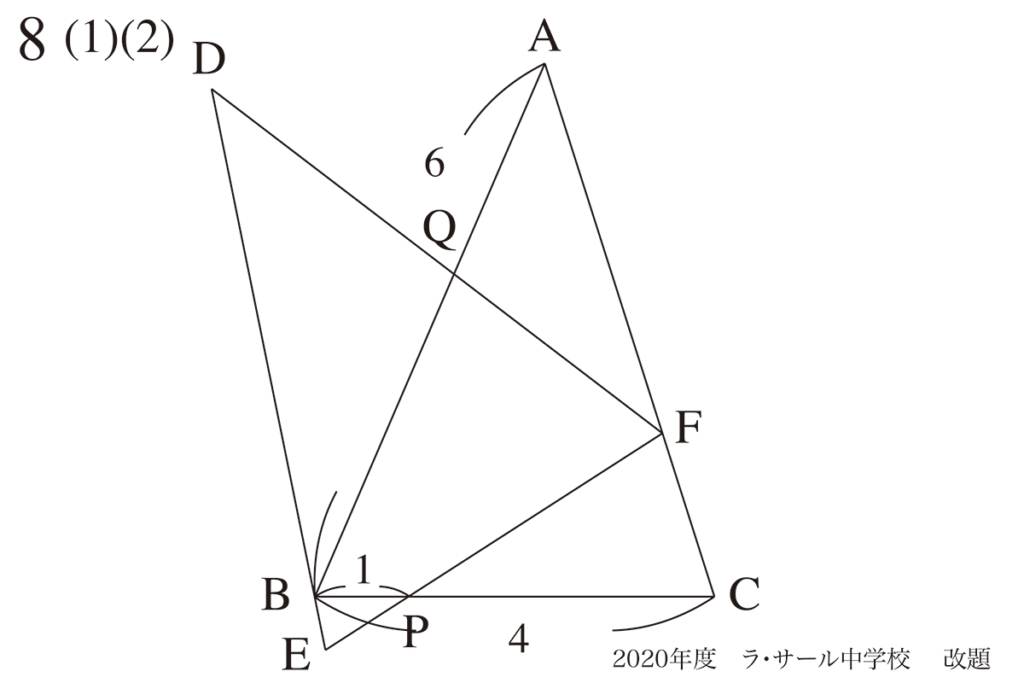
これで、(1)(2)を解くために、「見通しがだいぶ良くなった」のが実感できます。
図形を描いて状況を整理
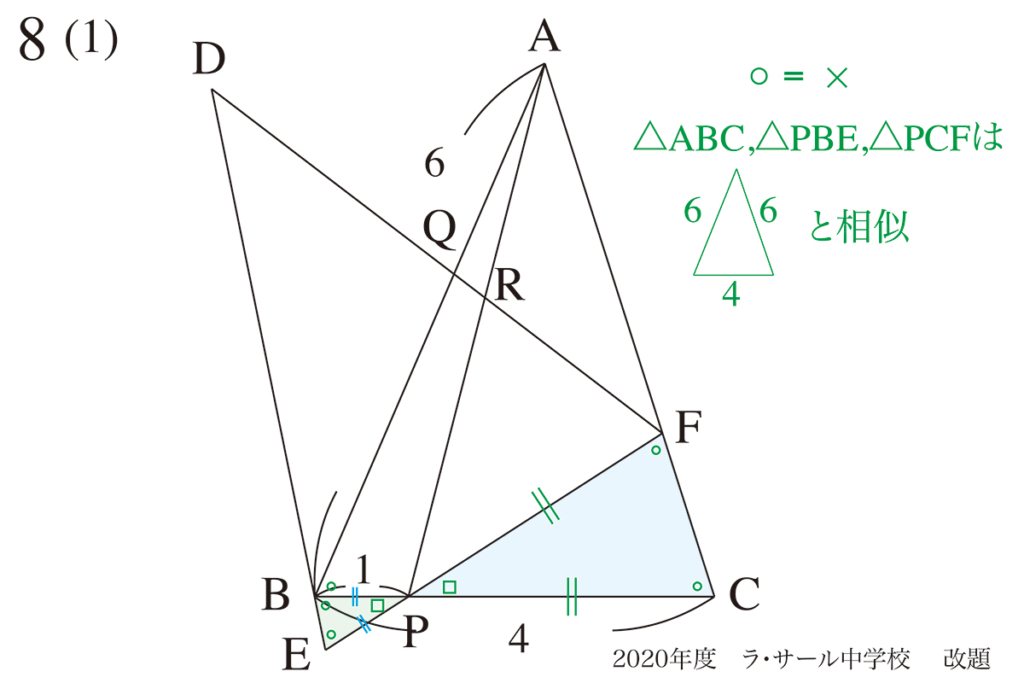
実は「APは原題にはなかった線」で、筆者が追加した線です。
男子小学生なんだ・・・
そうなんだ・・・
実は、こういうことは図形問題などでは、結構あることです。
線が一本なくなっただけでも、スッと見通しが良くなることがあります。
女子小学生でも、問題文に描かれている図形を
元に考えるから・・・
女子小学生こういう「邪魔な線を消す」は
気づかないかも・・・
問題文の図形とにらめっこしていても、なかなか気づかないことが多いです。
「自分で問題の図形を余白に描いてみる」も「解く鍵」が見つかる可能性があります。
自分で図形全体を描いたり、状況を整理すると、
男子小学生あれ？
最初はこの線は関係なさそうだ・・・
このように「気づく可能性」が、高くなります。
関係のない線などには消えてもらうと、見通しが良くなるでしょう。
スッキリと分かりやすい・考えやすい自分で描いた図形で考えてみましょう。
「自分で描いてみる」というちょっとした遠回りをすること。
それだけのことで、図形問題は「解法が見えてくる」可能性が高くなります。
日頃から、「自分で描く」練習をしておきましょう。
すると、試験の時も、図形をサッと短時間で描くことが出来るようになるでしょう。
この「描く時間」は「もったいない」のではなく、「描いている間に理解する」のです。
この意味では、「図形を描く」は「遠回りの近道」なのです。
・図形全体や問題文の状況を、自分で描く、整理する
・自分で描いて整理している間に、問題のポイントが分かる
・「自分で描く、整理すること」は時間がかかるけど、「遠回りの近道」
図形問題に出会ったら、図形を実際に描いたり頭の中でイメージして、
男子小学生図形を描いて、
イメージして、ポイントを理解しよう！
女子小学生どこが
ポイントで、何に着目したら解けるかな？
ポイントを意識して、問題に立ち向かって行くようにしましょう。
次回は下記リンクです。
