前回は「気持ちをきれいに整えて試験当日へ〜自分らしく「整った気持ち」・ミッドウェー島攻撃へ向かう友永隊・「美しすぎる」正三角形の編隊〜」の話でした。
大事な「勘」と図形の性質：比や数量は「思いこまない」で着実に
ms18_101ts
上の「正三角形が二つ」の部分の面積を考えました。
この問題の考え方は、上記リンクでご紹介しています。
この問題では、「面積比と辺の比の関係」が明示されているので、
男子小学生二つの大きな正三角形の
辺の比は６：５だ！
「二つの大きな正三角形辺の比は６：５」であることが、すぐに分かります。
ms18_110ts
そして、図形の中に様々な正三角形が見つかり、
男子小学生アとウの正三角形は、
「6 : 5」の正三角形の一部で、対称だから・・・
男子小学生アとウの正三角形の相似比も
「6 : 5」だ！
「他の正三角形の相似比（辺の比）も６：５」と思いこむと間違いです。
女子小学生勝手に思いこまないで、
きちんと考えるのが大事だね。
上の「正三角形二つ」の青色の部分を求める問題を考えました。
この問題の解き方は、上記リンクでご紹介しています。
・まずは「図形の性質」を考えて、図形の大事な性質を図形に描きこんで考える
・点と点を結んで、矢印を考えて「図形の位置関係」を考える
正三角形や正方形など「強い性質を持つ図形」が登場したときは、
男子小学生この辺の長さが全部
同じで、角度も同じ・・・
図形の性質を、しっかり描きこんで考えるのが大事です。
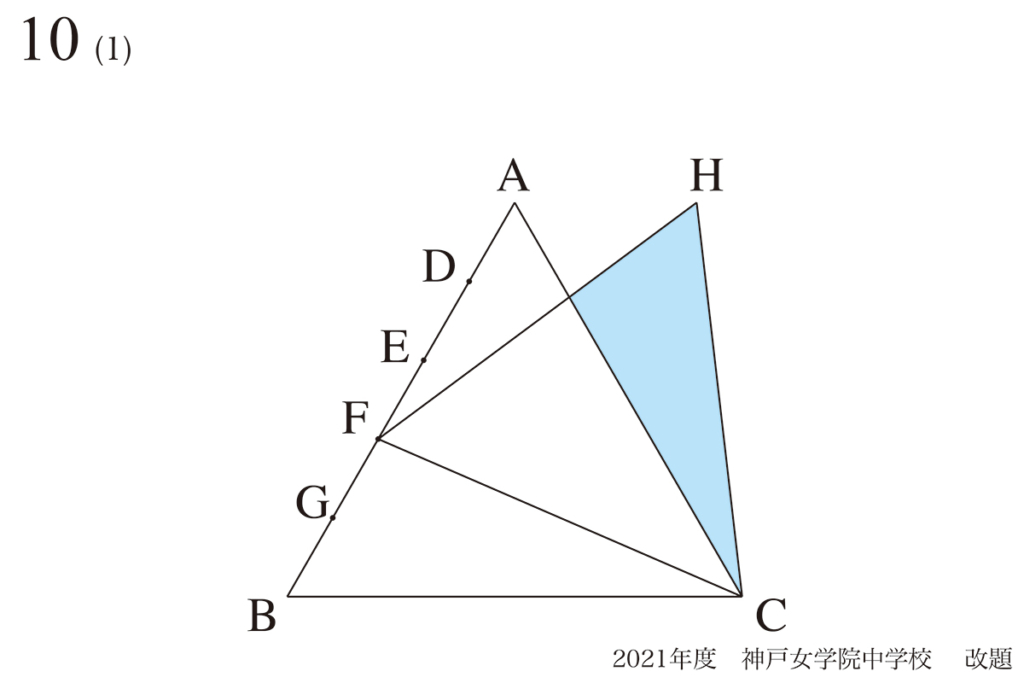
この様に「動く点」や「動く図形」の問題を考える時は、「矢印の考え方」が良いです。
ここでは、上の図のように「AHを結ぶ補助線」を引いた後に、
男子小学生なんか、AHと
BCって平行っぽいけど・・・
「AHとBCが平行」ならば、「錯角で角HAC=角ACB」なので、「角HACは60度」になるはずです。
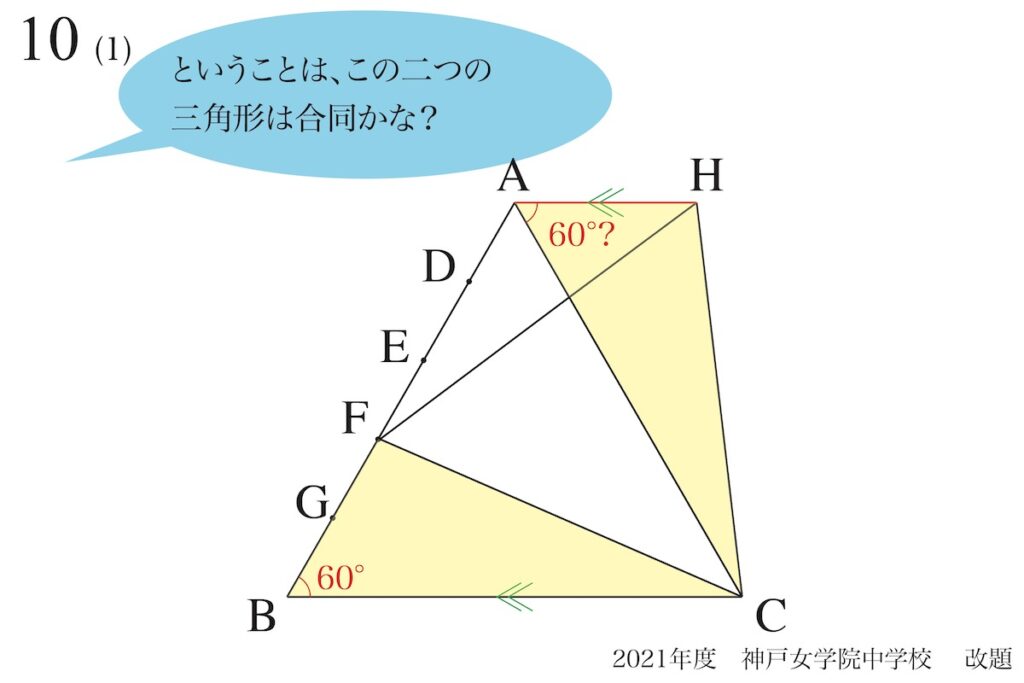
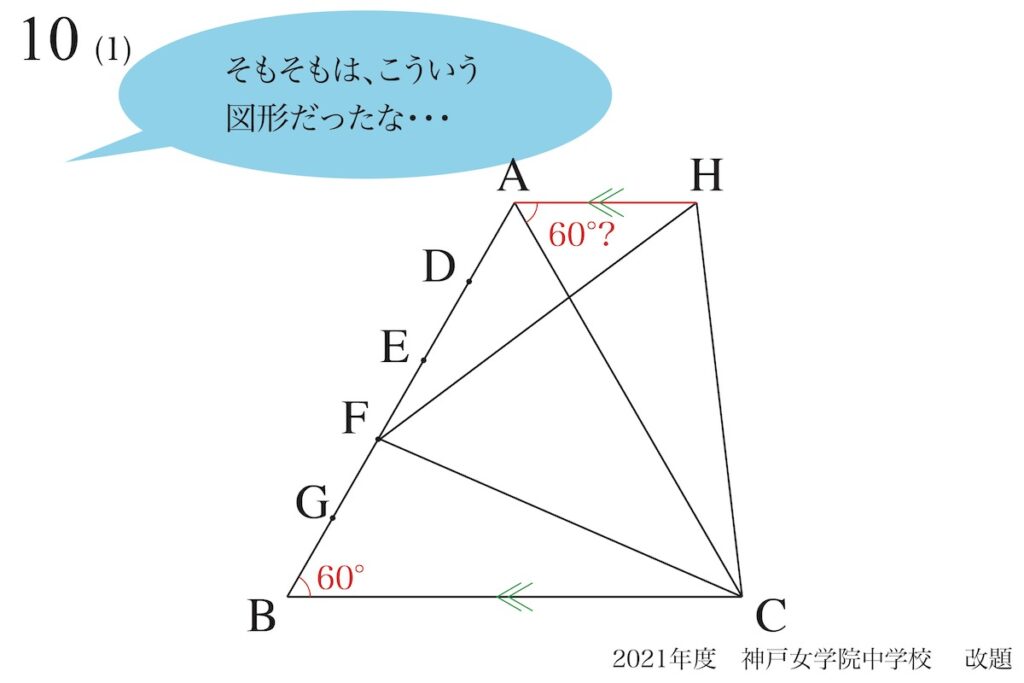
「AHとBCが平行」とすると、上の二つの黄色の三角形は同じ（合同）です。
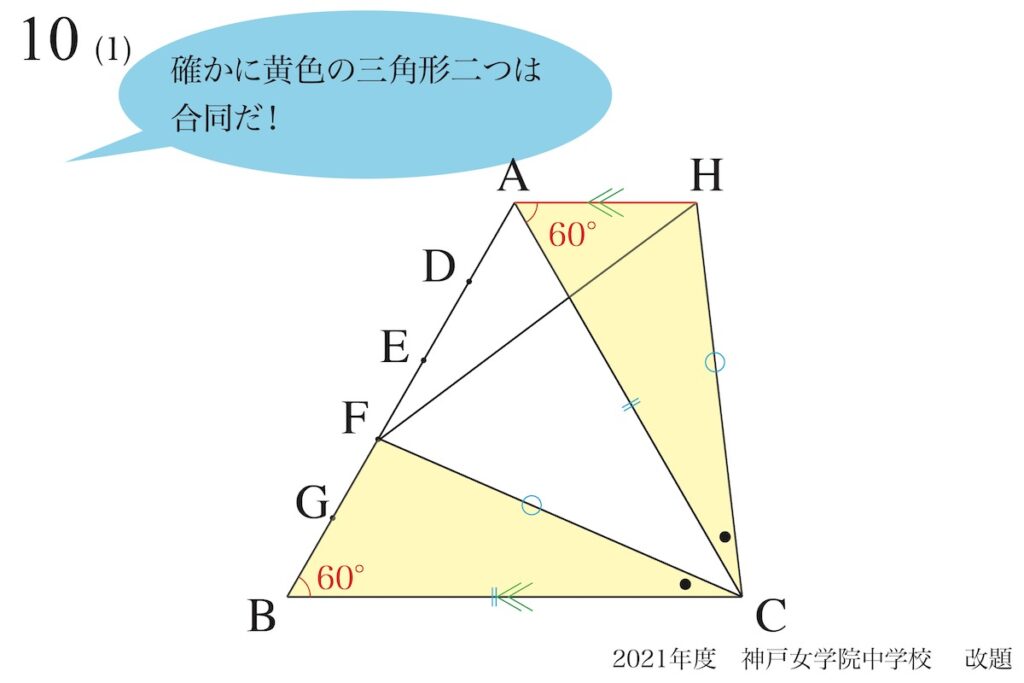
男子小学生確かに
二つの黄色の三角形は同じだ！
男子小学生だから、「AHとBCが平行」は
確かに合っている！
「AHとBCが平行」として考えると、整合性が取れているのでOKです。
この「AHとBCが平行」として考える話を上記リンクでご紹介しています。
ここでは、簡単な図形が二つ〜三つあって「複雑に見える」時の考え方もご紹介しています。
女子小学生この時は、「AHとBCが平行」と
思いこんで良かったんだね！
性質の場合は、「思いこみ」というより「勘」を大事にしましょう。
図形などの性質は「勘が正しい」ことも多いですが、比や数量は「思いこみは大体誤り」の傾向があります。
・平行などの「勘」を大事に
・比などの数字・数量は「思いこみ」ではなく、きちんと着実に考えて計算
極めて強い「合格する」思いこみ+「思いこみで解かない」で合格へ
算数に限らず、他の科目でも直感や勘は大事です。
男子小学生ここは
こうじゃないかな・・・
女子小学生きっと、この問題は
こうだと思う！
学ぶプロセスでは「理由」は、とても大事ですが、時間が限られた試験では、
女子小学生理由は、ちょっと
分からないけど・・・
「理由が分からない」でも「合っていれば良い」こともあります。
「自分の直感や勘」を大事に信じる姿勢と、比や数量などは「思いこみで解かない」姿勢が大事です。
そして、最も大事なことは「合格すると強く思いこむ」ことです。
男子小学生僕は絶対、絶対に
X中学に合格する！
女子小学生私は絶対、絶対に
Y中学に合格出来る！
「合格する」という極めて強い思いこみと「思いこみで解かない」ことを心がけましょう。
この「思いこむ」姿勢と「思いこまない」姿勢を合わせて、合格に向かいましょう。
読者の皆様の志望校合格を、心より願っております。
