前回は「算数の学力の伸ばし方〜同じように考える姿勢・大事なポイントを意識して学力アップ・横断的に考える視点・問題ごとの解法ではなく大事な「共通する考え方」・様々な図形と様々な解き方〜」の話でした。
補助線を発見する考え方
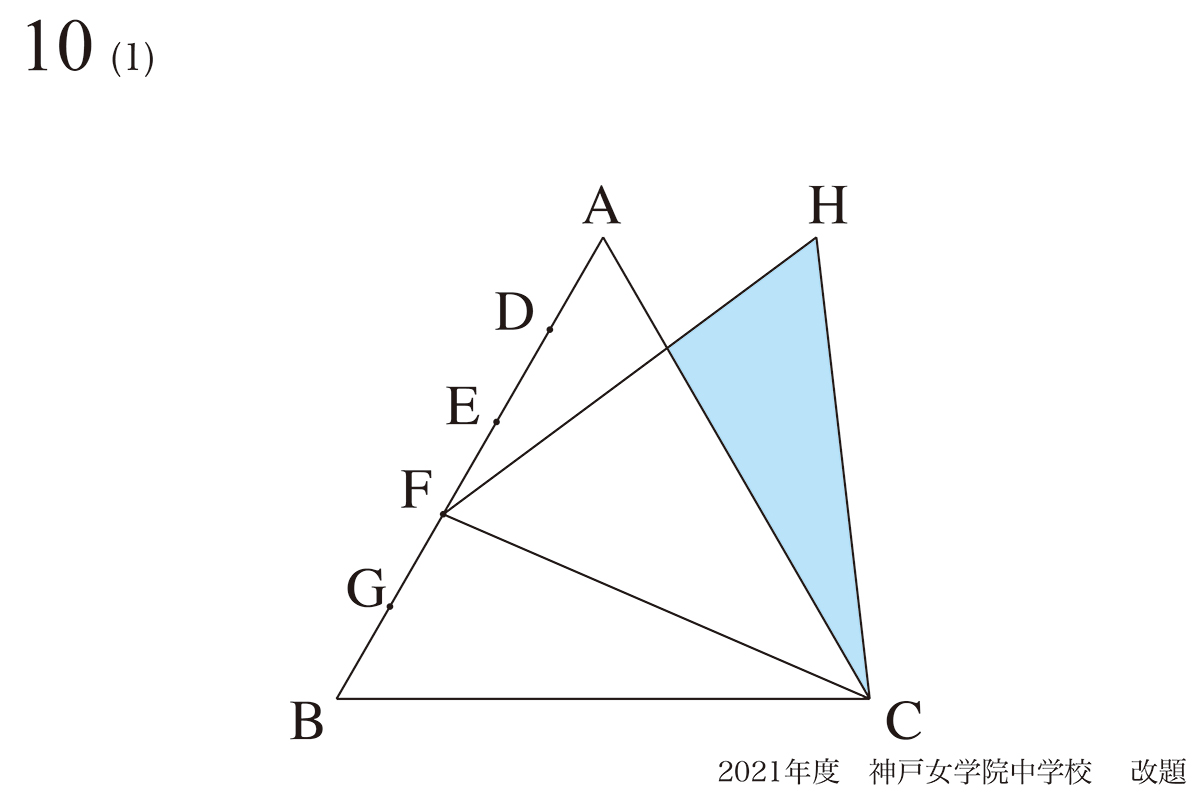
今回は「補助線をどのように発見するか」を具体的に考えてみましょう。
算数実践で問題10の図形問題をもう一度考えてみましょう。
「正三角形が2つ」という極めてシンプルであり、図形の大事な要素が沢山ある良い問題です。
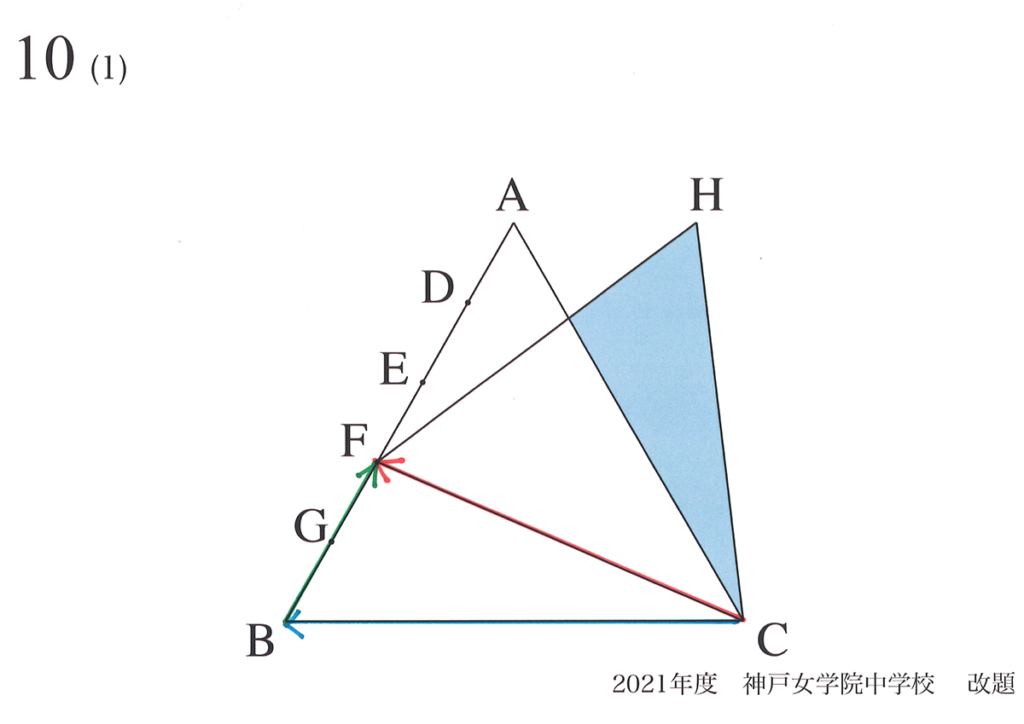
この問題では「辺を矢印に置き換える」考え方をご紹介しました。
上の図のように「矢印CF=矢印CB+矢印BF」と考えました。
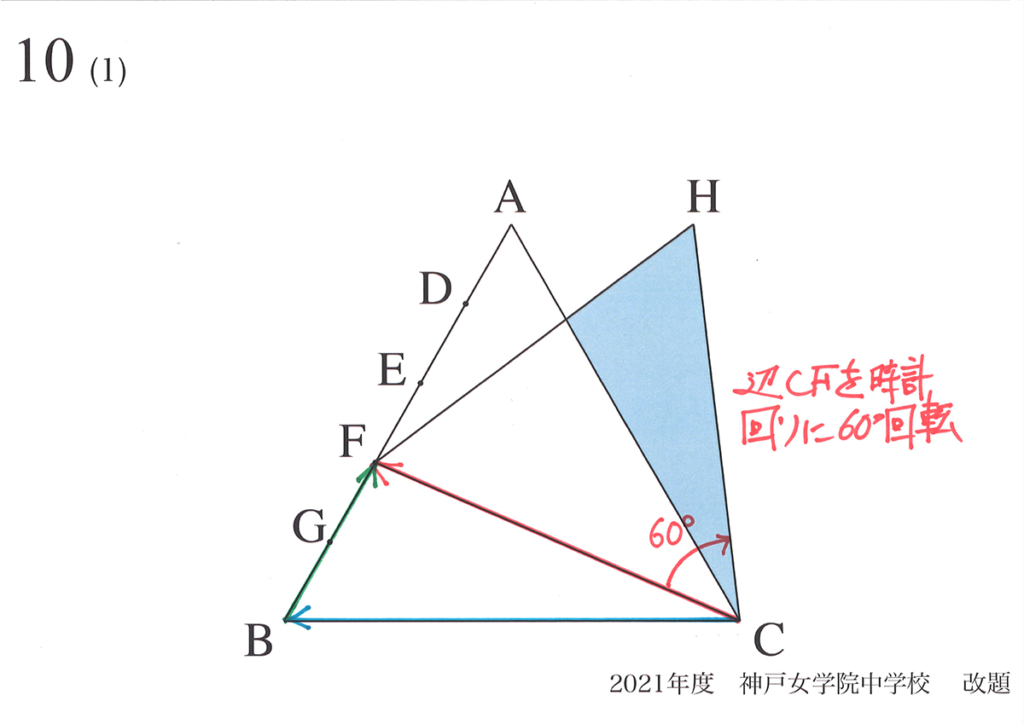
そして、正三角形HFCが新たに出来る過程を追いかけました。
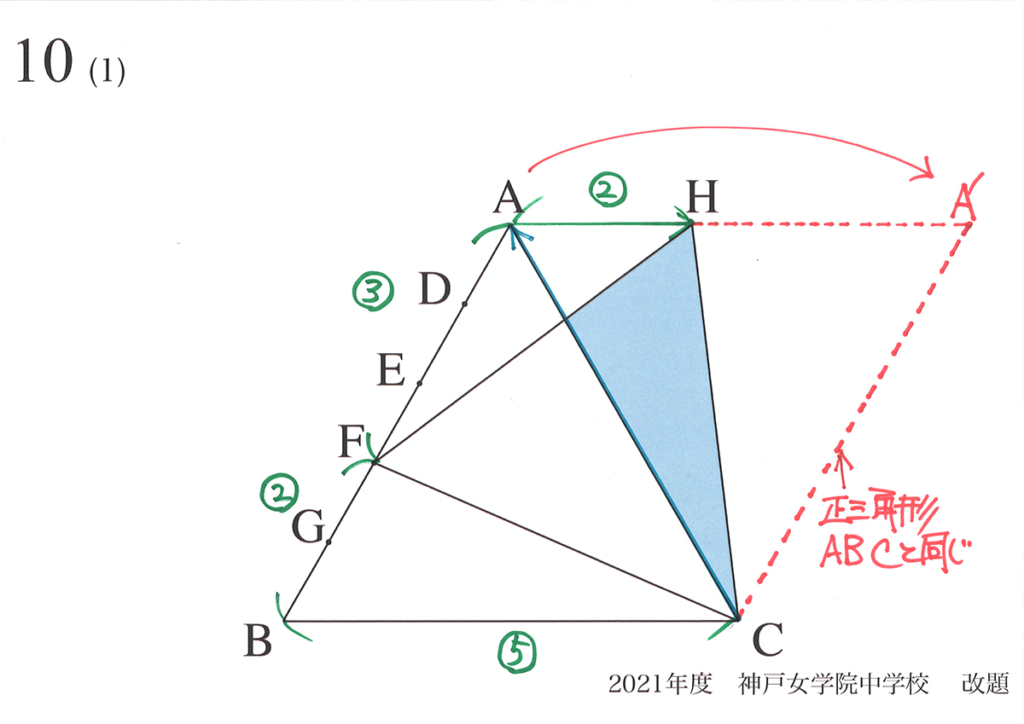
すると、「三角形HACは三角形FBCと同じ（合同）」であることに気づき、解く鍵が分かりました。
この問題の考え方は、上記リンクでご紹介しています。
筆者は「矢印の考え方」が最もお勧めであると考えますが、「小学生の範囲を超えている」面があります。
そこで、「補助線を引く」解法を考えて、どのように「補助線を発見するのか」を考えます。
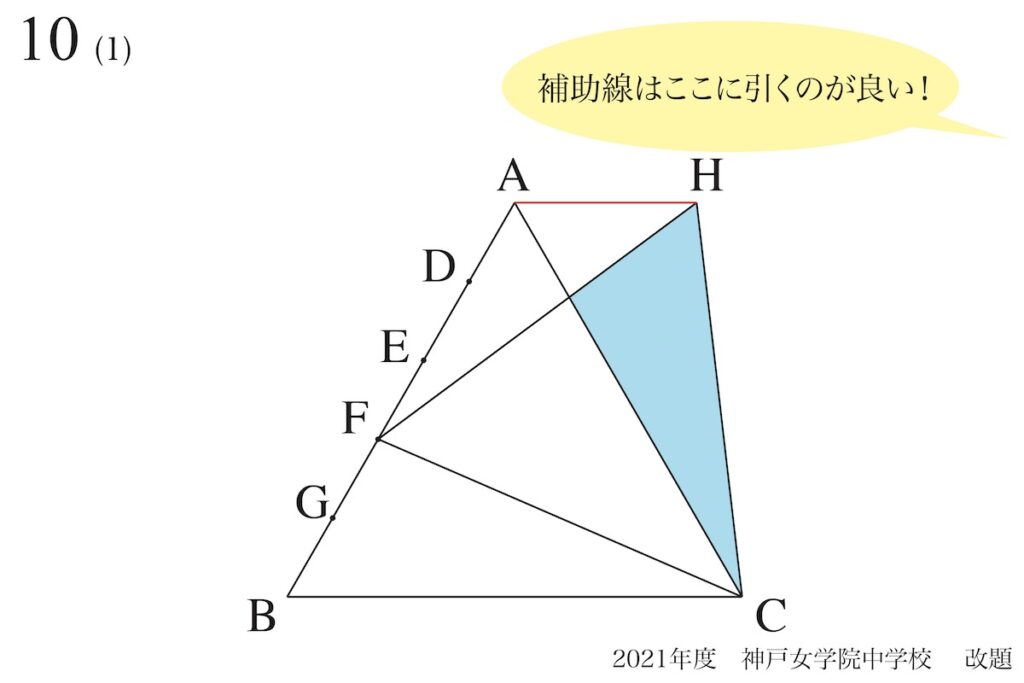
最も多い補助線は、上図の「AHをつないだ補助線」でしょう。
塾講師補助線は
ここがベスト！
この問題を一度教われば、「補助線の位置=AH」は比較的分かりやすいです。
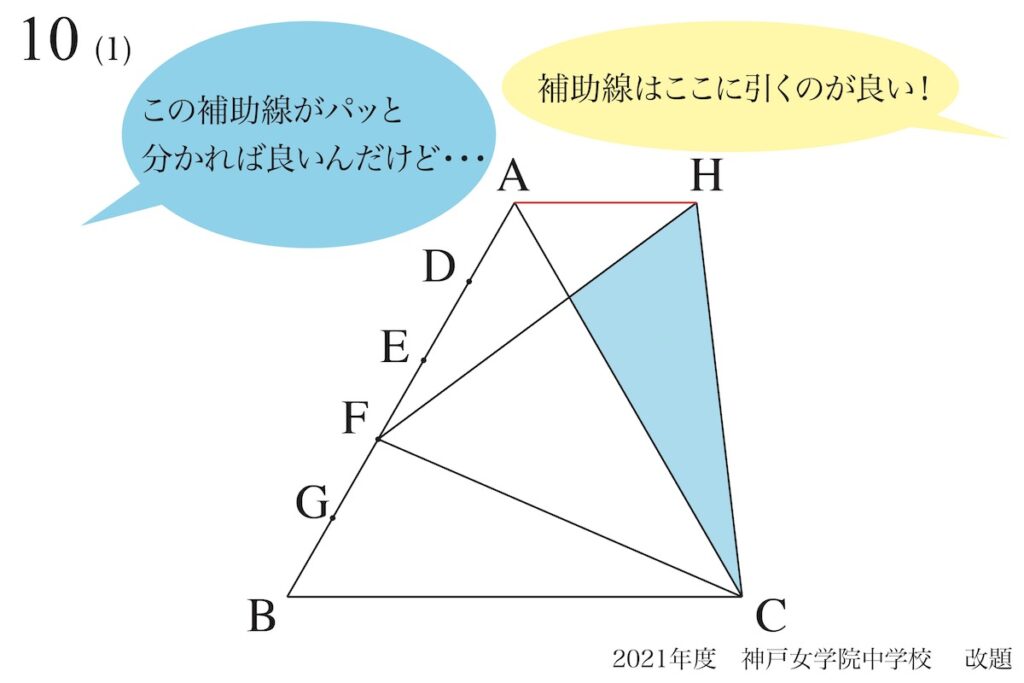
ところが、この問題が「初めて見る問題だったら、補助線をどう思いつくか」が大きな問題です。
男子小学生やっぱり、
補助線にはセンスが必要なのかな？
女子小学生こういう補助線を
パッと思いつくようになりたい・・・
受験生後半〜直前期になると、「どう問題が素早く解けるか」が大事なポイントになります。
「ちょっとしたこと」に気づくことで、問題が一気に見えて解けるようになることがある算数。
この問題は他にも有効な補助線があるでしょうが、「補助線AH」に気付けば全て解けます。
男子小学生どうやって、
この補助線を思いつくのかな・・・
今回は、この図形を異なる視点から考えてみましょう。
図形の線を消してみる発想：「出っぱった図形を整理」する発想
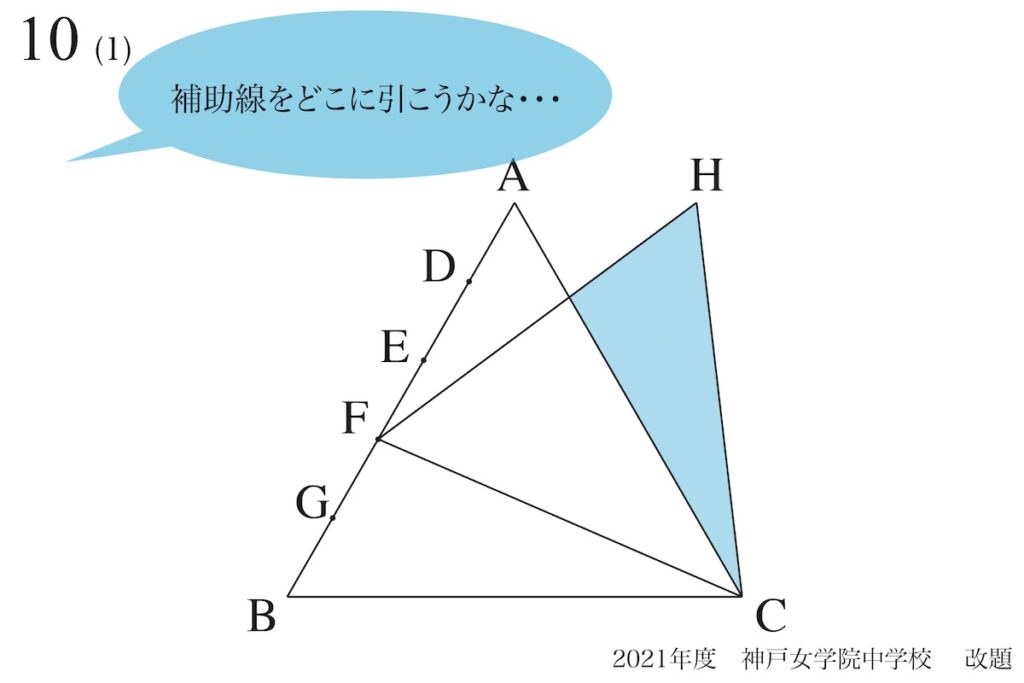
元の図形に戻って、「補助線どこに引こうかな」と悩んでいる状況を考えましょう。
この図形の正体は「二つの正三角形」であり、非常に分かりやすいです。
「分かりやすい形=正三角形」だからこそ、この図形の正体が「分かる」のに「分からない」状況です。
この「分かるのに分からない」状況こそが、算数・数学、理科・物理で大変多いことです。
ここで「分かる」と楽しくなるのですが、「分からない」と楽しくなくなるのが算数・数学です。
男子小学生良い補助線を
発見するぞ！
このように力んでしまう方が多いですが、少し「違う視点」で考えましょう。
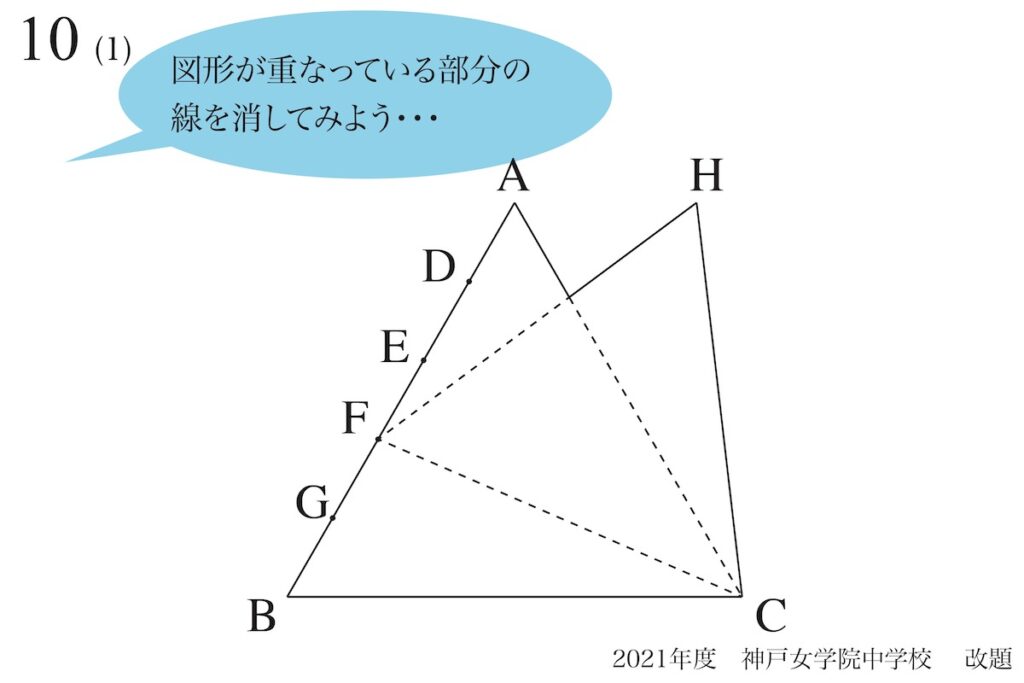
この図形は「正三角形2つ」ですが、図形自体を考えるために、内部の線を消してみましょう。
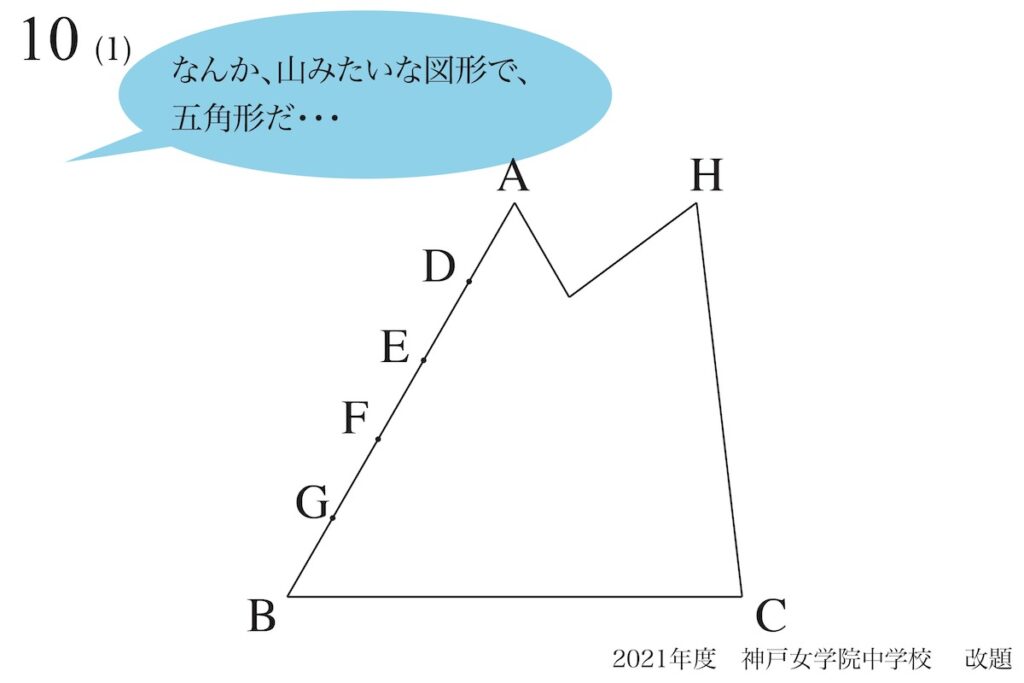
消したら、上図のような「山みたいな五角形」になります。
男子小学生なんか、山みたいで、
2本の角（つの）みたいだね・・・
女子小学生「正三角形2つ」だったのに、
分かりにくくなった気がするけど・・・
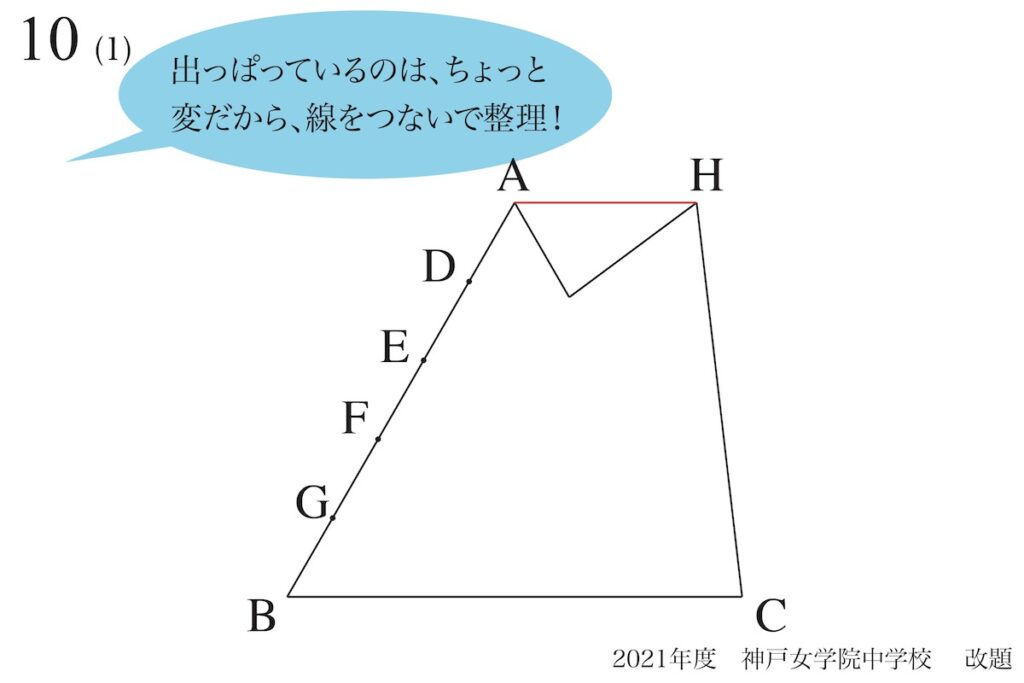
ここで「出っぱっている図形」は扱いにくく変なので、「出っぱり同士」をつなぎましょう。
すると、「四角形の穏やかな図形」が見えてきました。
三角形・四角形までは「分かりやすい」図形ですが、五角形以上になると複雑に見えます。
そこで、「出っぱっている五角形」に補助線を加えて「分かりやすい四角形」にしました。
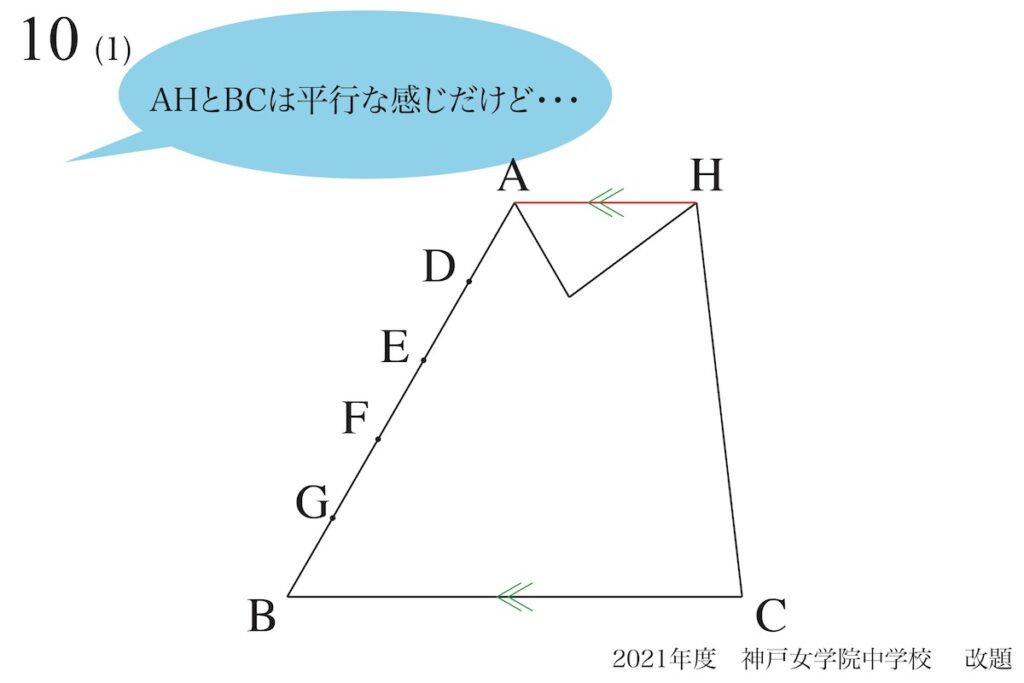
ここで「図形的発想」が思いつけば良いですが、
女子小学生AHとBCが平行な
気がする・・・
「ひょっとしたら」と気づく方が多いでしょう。
この時、「分からなければ」と思わず「そんな気がする」で良いでしょう。
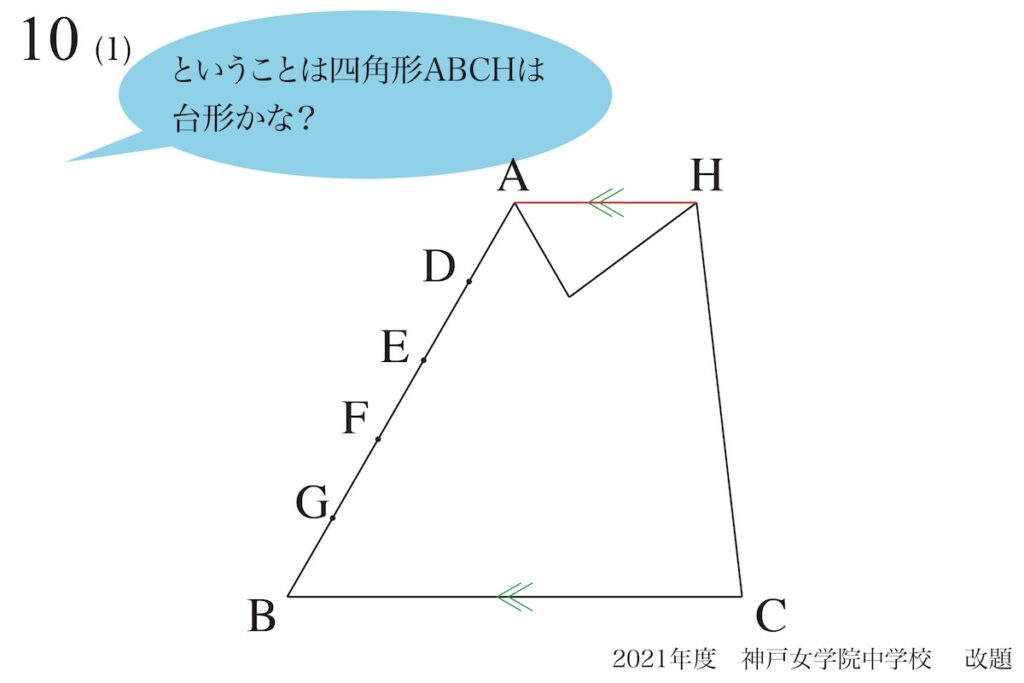
もし、AHとBCが平行ならば、四角形ABCHは台形のはずです。
ここまでは「確信が持てない状況」でも良いので、
女子小学生この図形は台形？
合ってるかな？
「そうかな？」くらいで考えましょう。
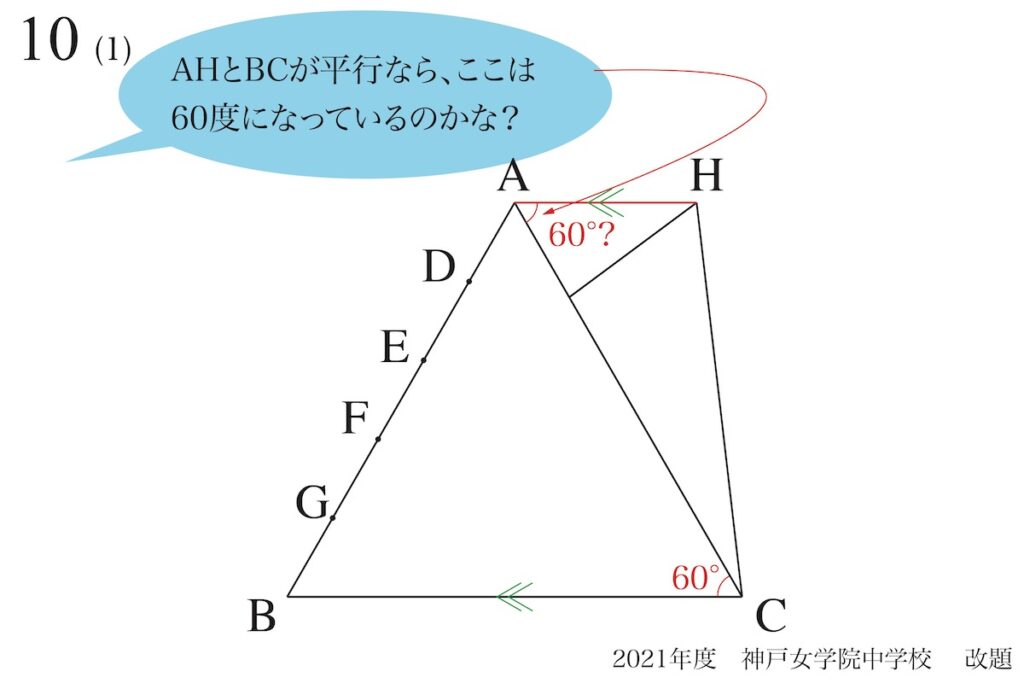
もし、「AHとBCが平行」であれば、上図のように錯角から「角HAC=60度」となります。
この時点でも、
女子小学生こういうことに
なるかな？
まだ「？」が残っていて良いでしょう。
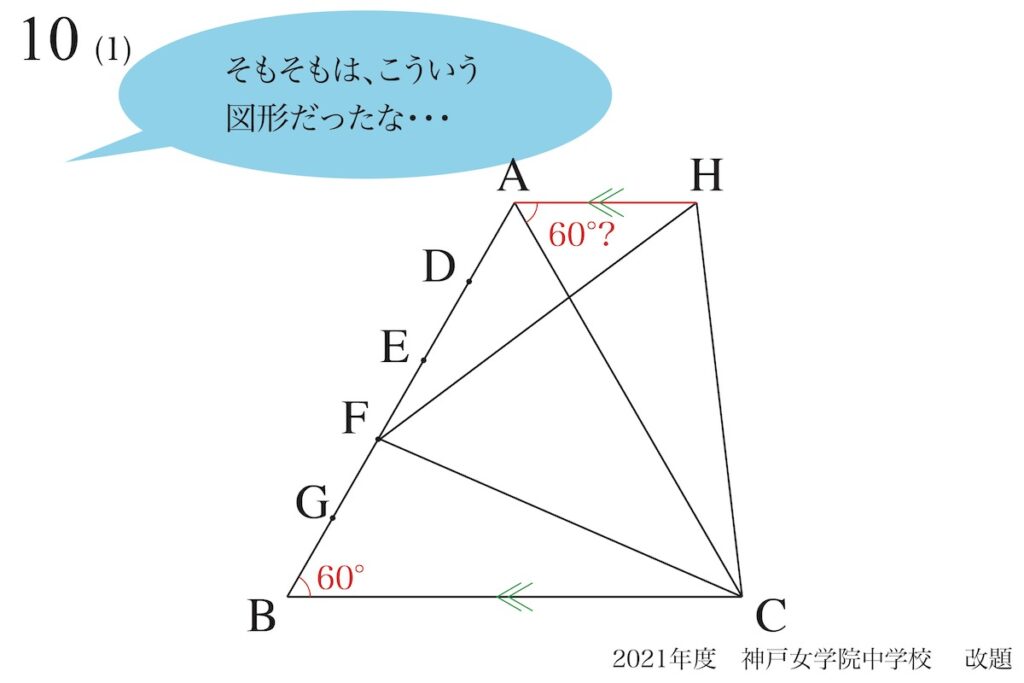
ここで、元の図形に戻ってみると、60度が沢山見えてきます。
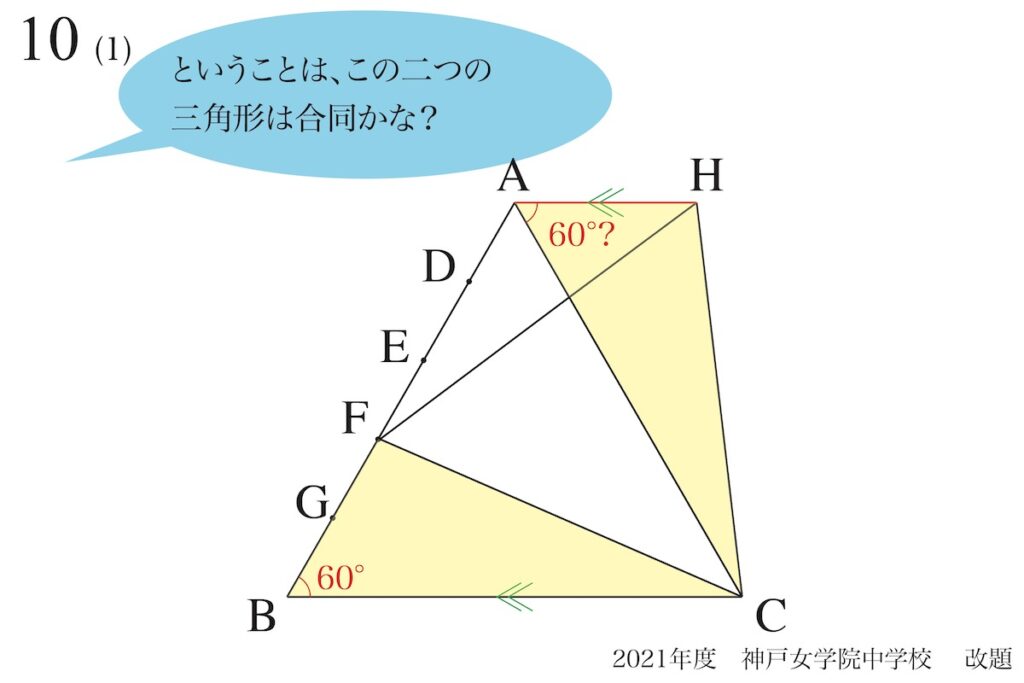
すると、上図の二つの黄色の三角形が同じ（合同）に見えてきます。
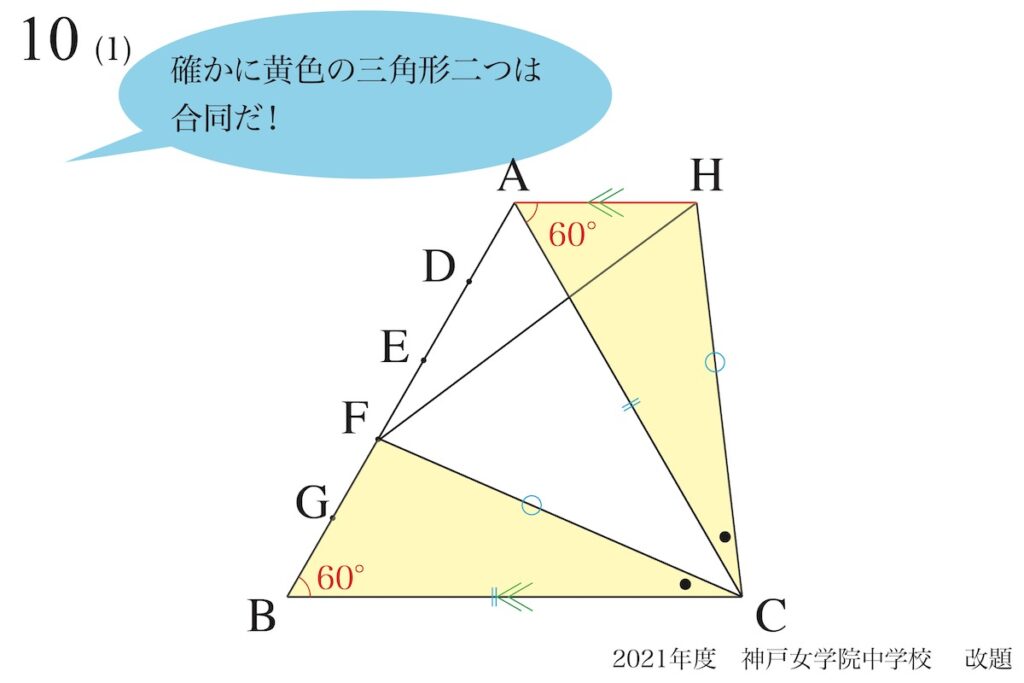
ここで、「正三角形の辺の長さが等しい」を考えると、黄色の三角形が合同であることが分かります。
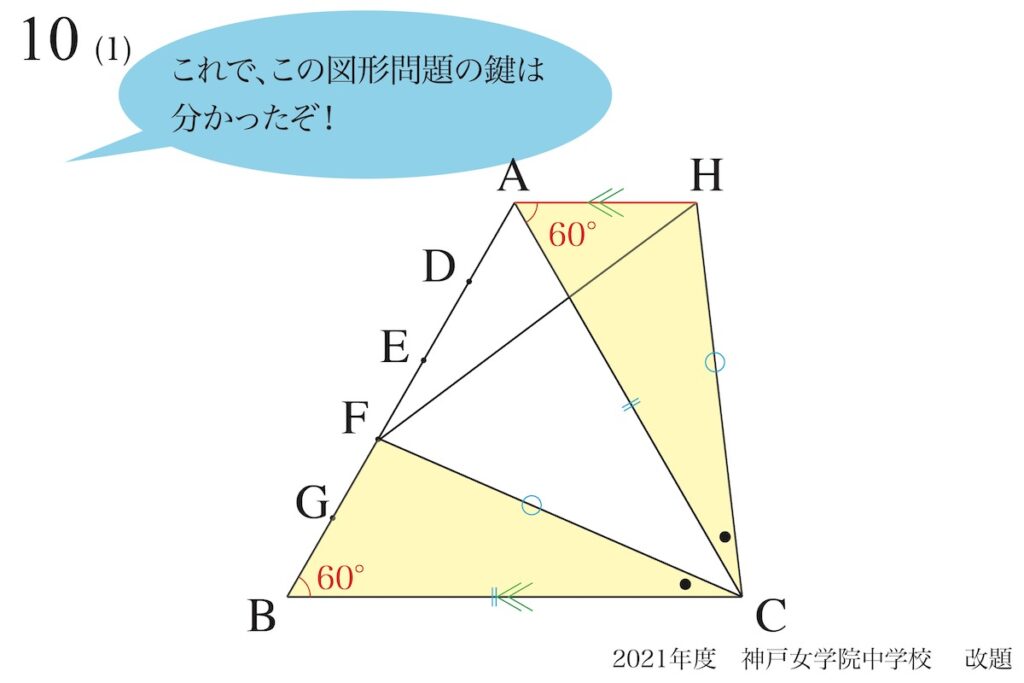
黄色の2つの三角形が合同であることが分かれば、最初の「AHとBCは平行」も分かります。
ここから先は、上記リンクをご覧ください。
男子小学生なんか、
面白いね・・・
女子小学生線を消して、図形そのものの形を考えて、
補助線を思いついた感じだね・・・
「正三角形が2つ」という状況を、線を消すと「よく分からない五角形」になりました。
そこで、「出っぱった図形を整理」する発想を思いつきました。
この考え方は少し長く説明しましたが、こういう思考を素早く出来ると良いでしょう。
「物事を異なる角度から見る」ことは非常に本質的なことで、算数・数学では大事です。
・図形の線を消したり、足したり（補助線）してみる
・異なる視点や角度から見たり、考える思考
整理する発想と解き方：変わったポイントと「解く鍵」
中学受験生・高校受験生・大学受験生の頭の中には沢山の「考え方」が入っています。
上の例は中学受験生ですが、大学受験生なら「数列・微分・積分・複素数」などになります。
これらの「思考の引き出し」を沢山作ることが「一つの学び方」になります。
ところが、これらの引き出しは「学んでいるうちにバラバラになる」傾向があります。
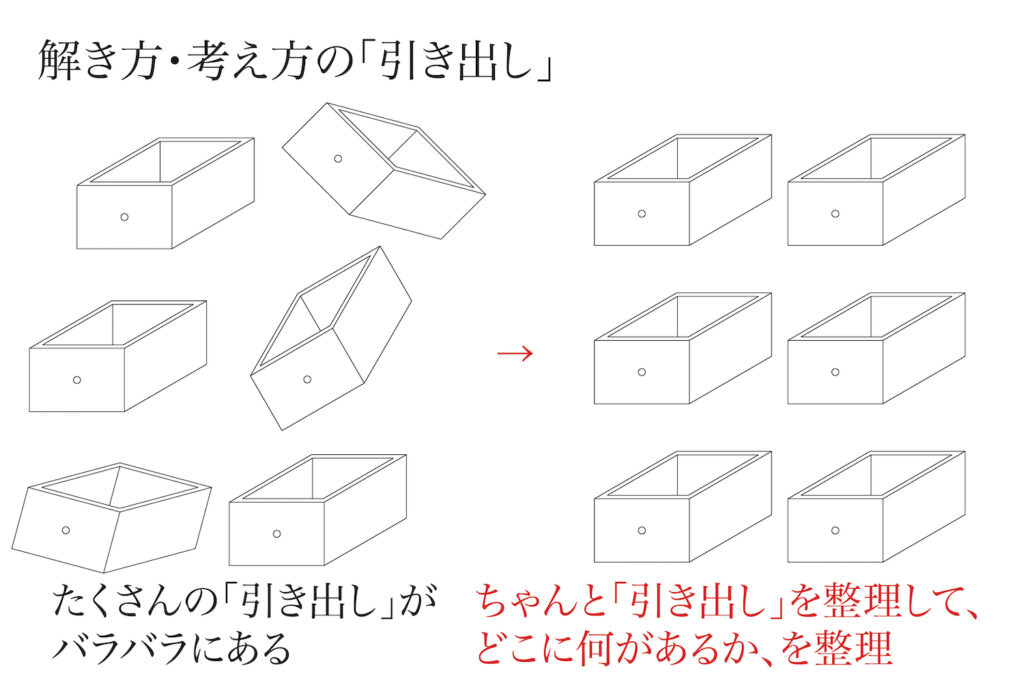
バラバラになった引き出しは、整理整頓して「どこに何があるか」を整理しましょう。
思考を整理する話を上記リンクでご紹介しています。
受験期後半〜直前期は、この「思考の発想の引き出しを整理」する学び方が大事です。
ひたすら問題を沢山解いても、「考え方や思考の引き出し」がバラバラだと解けない可能性があります。
小学生・中学生の方は親から、
受験生の母親ちょっと、これらの本や
おもちゃをすぐ片づけなさい！
このように「片付ける」ように怒られた経験がある方が多いでしょう。
こう親に言われると、
男子小学生分かっているよ・・・
はあ〜大変だな・・・
誰しもこう思いますが、実際に整理整頓してみると、
男子小学生やっぱり、整理整頓されている方が、
きれいだし、どこに何があるか分かるからいいかも・・・
やはり整理されている部屋の方が良いです。
問題を解く時も同じで、「整理整頓されている方が良い」のです。
引き出しを沢山作って、整理整頓しておけば、どんな問題が出てきても解けるでしょう。
この「引き出し」は「全く新しい引き出しをつくろう」より「「引き出しを大きくしよう」が良いでしょう。
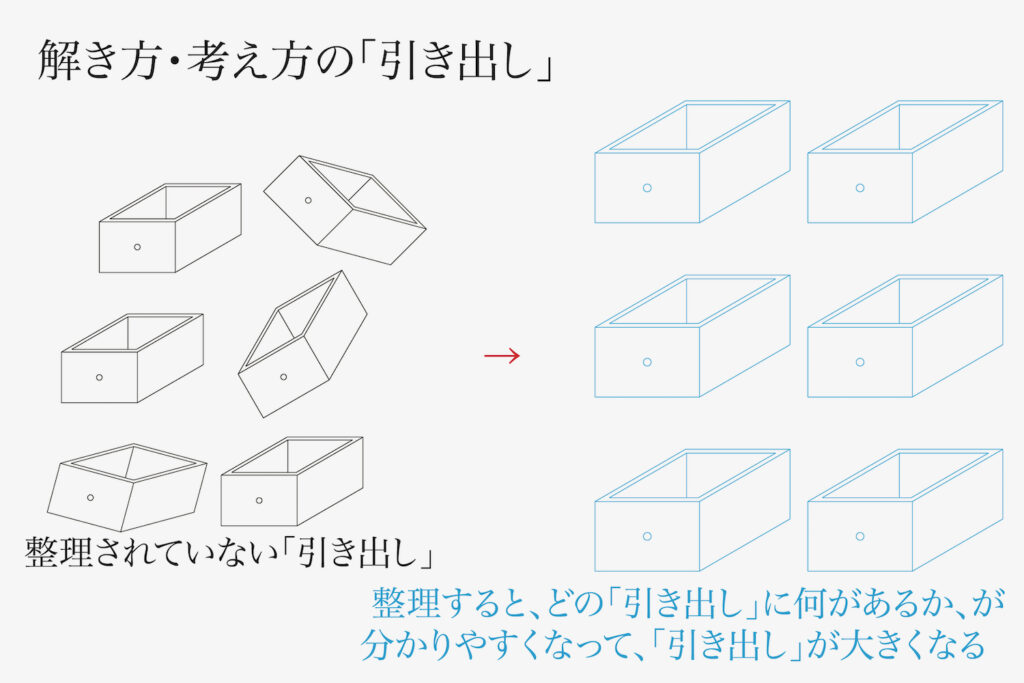
思考の引き出しを大きくすると、「解法の幅」が広がり学力が上がるでしょう。
上の図形問題の考え方は「一つの考え方」であり、賛否両論あるでしょう。
いずれにしても、ある考え方を身につけたら「自分なり」が一番良いでしょう。
自分なりに色々考えてみると、一題の問題から多くを学ぶでしょう。
上の図形では、線を消したら「変な図形」が出てきました。
「変な図形」の「最も変なところ=出っぱり」に補助線を引いて整理整頓したイメージです。
このように視点を変えて、「変なところ」や「変わったところ（変化したところ）」はポイントです。
両方とも「変」がつきますが、「変や変化」は算数・理科のポイントです。
・視点を変えて「変なところ」や「変わった（変化した）ところ」に注目
・気づいた点を考えると「解く鍵」につながることが多い
変な・変わった（変化した）ポイントに注目すると、様々な分野の学力が上がるでしょう。
ニュートン算・流水算・旅人算・比・・・色々な問題が、この「変わった視点に注目」で解けるでしょう。
このように応用問題などで、しっかりとした視点で考えて解くと学力は飛躍的に上がるでしょう。
次回は下記リンクです。
