前回は「動く図形を描いて得意になるポイント・コツ〜実際に自分で描く姿勢・定規を使って正確に作図・図形を頭と身体で理解・まずは描いてみる姿勢・問題14(1)(2)(3)・(1)解法〜」の話でした。
問題14(1)(2)(3)(再掲載)
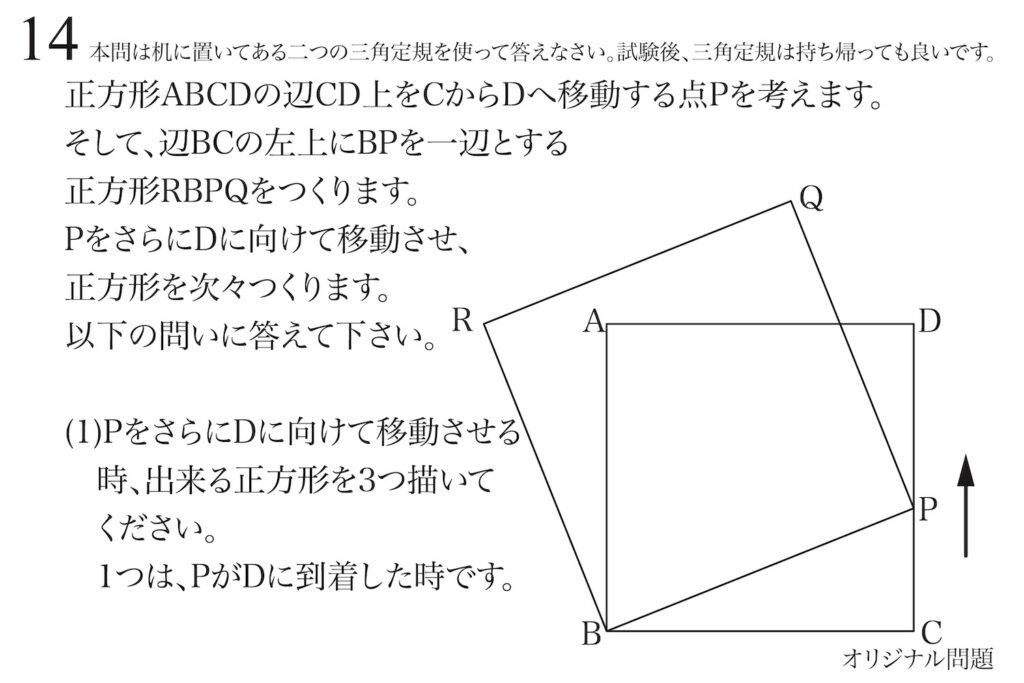
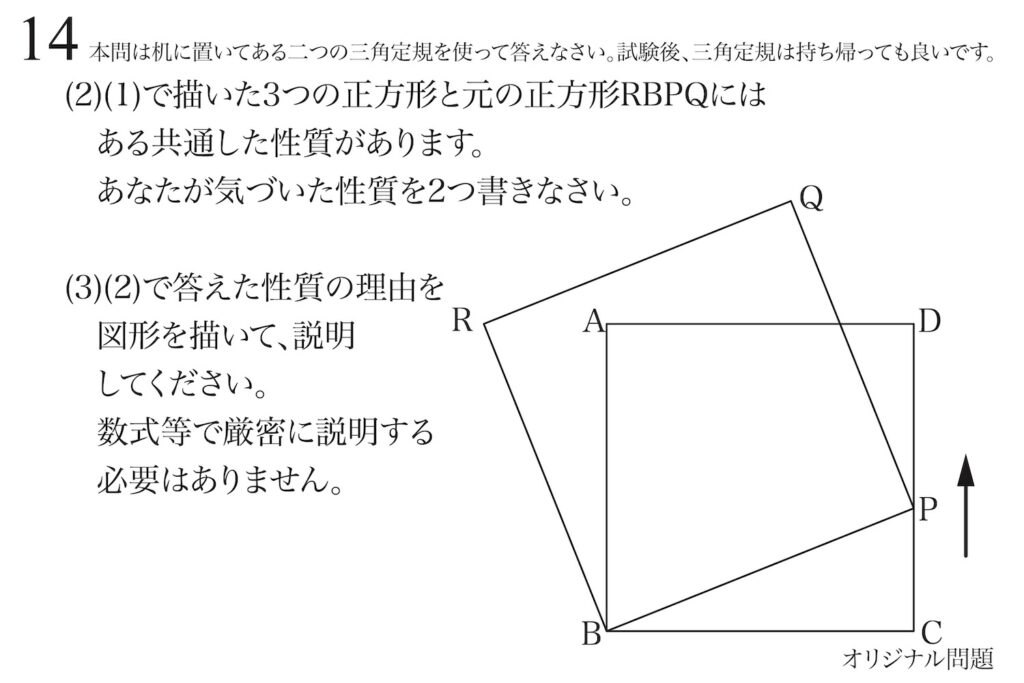
動く点と図形を理解するポイント:新たに出来る正方形の特徴
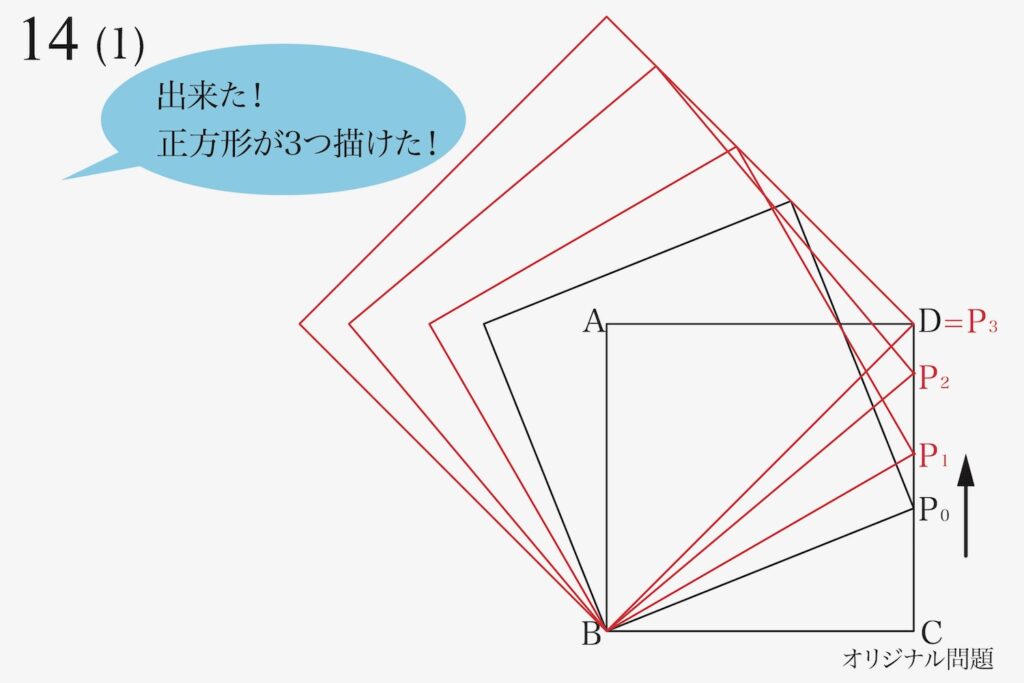
動く点Pが辺CD上を点Cから点Dへ移動して行き、左上に次々と正方形が作られて行きます。
 男子小学生
男子小学生こんな風に
なるんだね!



最初描いてみた時は、
本当?って思った・・・

今回は、動く点Pと新たに出来る正方形の全体像から「図形の特徴」を考えてみましょう。
動く点Pの最初の位置をP0として、「順にP1、P2、P3=Dと移動する」と考えます。
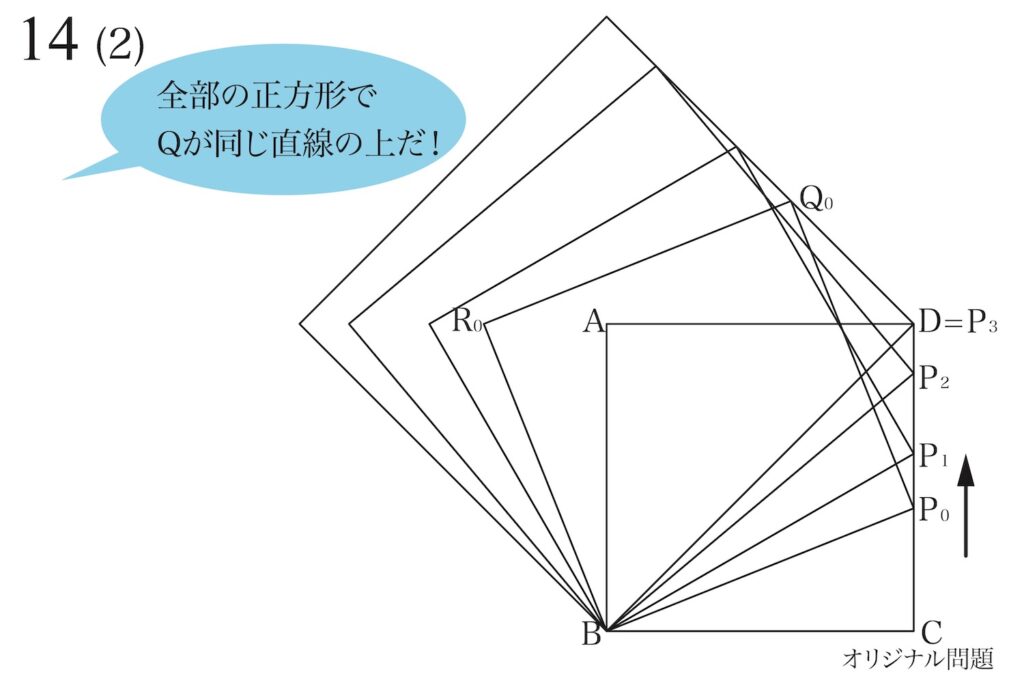

新たに出来る正方形の右上の点である点Qが「全て同じ直線の上」です。
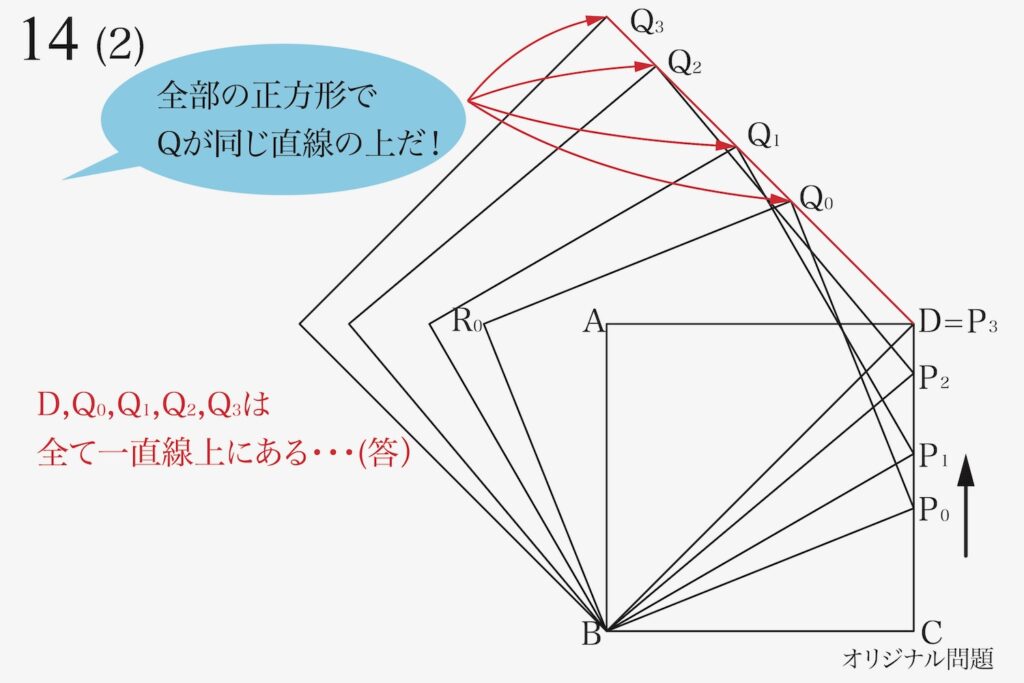

問題文によりますが、今回のように「図形の特徴を答える」時には、自分で点に名前をつけましょう。
「移動する点」の時は、「移動に合わせて、点の名前に添字をつける」のが一つの考え方です。
「点PがP0から順にP1、P2、P3=Dと移動」するにつれて、「点QがQ0から順にQ1、Q2、Q3と移動」としましょう。
すると、(2)の答えの一つは、「点D、Q0、Q1、Q2、Q3は全て(同一)の一直線上にある」です。
図形の特徴を探る姿勢:直線と角度に注目


最も気付きやすい特徴は、点Qの移動です。
この図形の他の特徴を考えてみましょう。



他に
あるの?



図形の特徴って、
どういうことを考えたらいいのかな?
まず、図形の特徴を考えてみましょう。
・辺や直線の長さに共通点
・辺と辺や二直線の角度に共通点
直線と角度を考えると図形を描くことが出来ます。
そこで、図形を考えるときは「辺や直線の長さ」と「辺と辺や二直線の角度」を考えましょう。
今回考えている正方形は「辺や直線の長さ、辺と辺や二直線の角度が全て同じ(同一)」です。
今回のように、「図形が新たに出来る」時の特徴は「点が同一直線上にある」などを考えましょう。
・共通する性質の点が同じ(同一)の直線上にある(直線は見えない場合がある)
・共通する性質の点が同じ(同一)の方向・角度を向いている
「何かの直線上にある」ことと「同じ方向・角度を向いている」は同じことを意味することもあります。
まずは、「点が同じ直線上にないか?」を考えましょう。



これは、
もうないね・・・



ちょっと待って・・・
直線って「まだ見えてない」かも・・・



あっ、ひょっとしたら
この直線はどうかな?
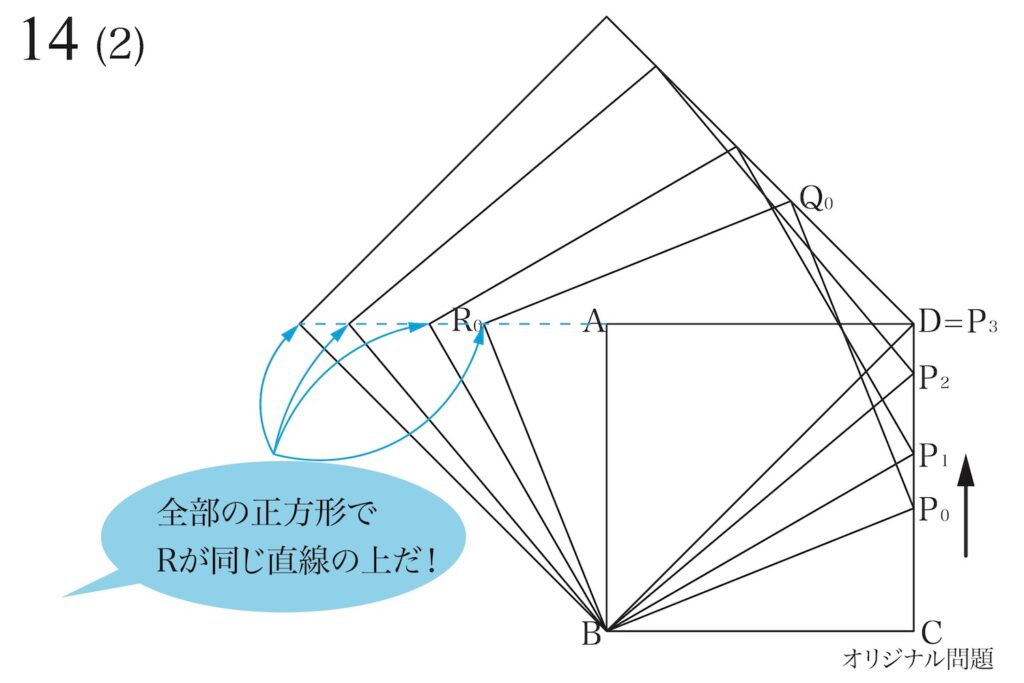




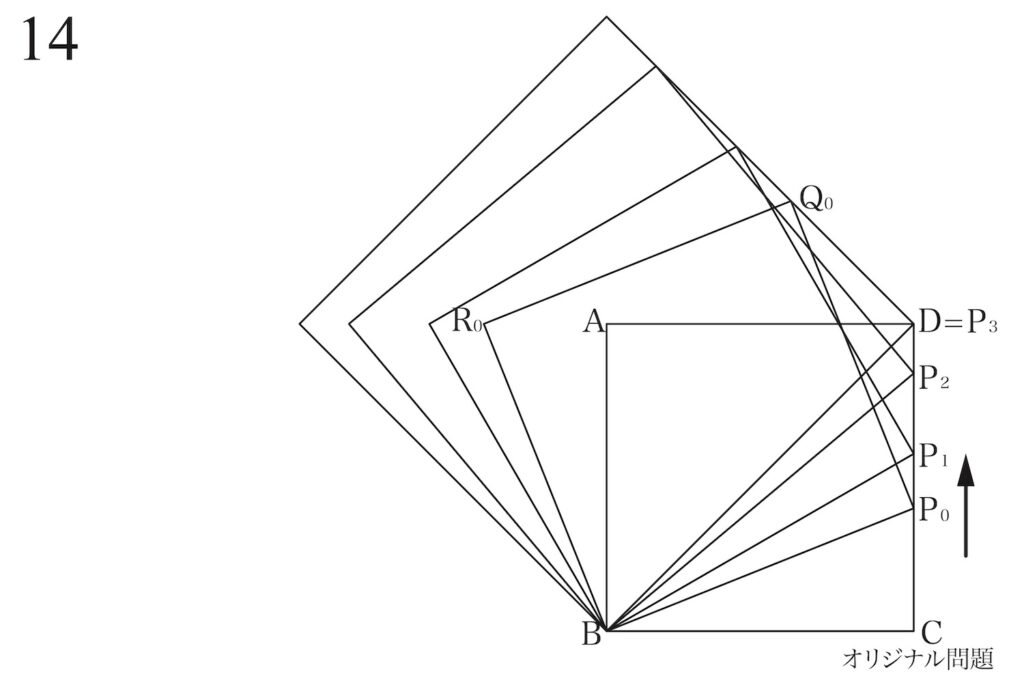
この点Rは
全部この点線の上にあるんじゃない?



確かに
そうだね!
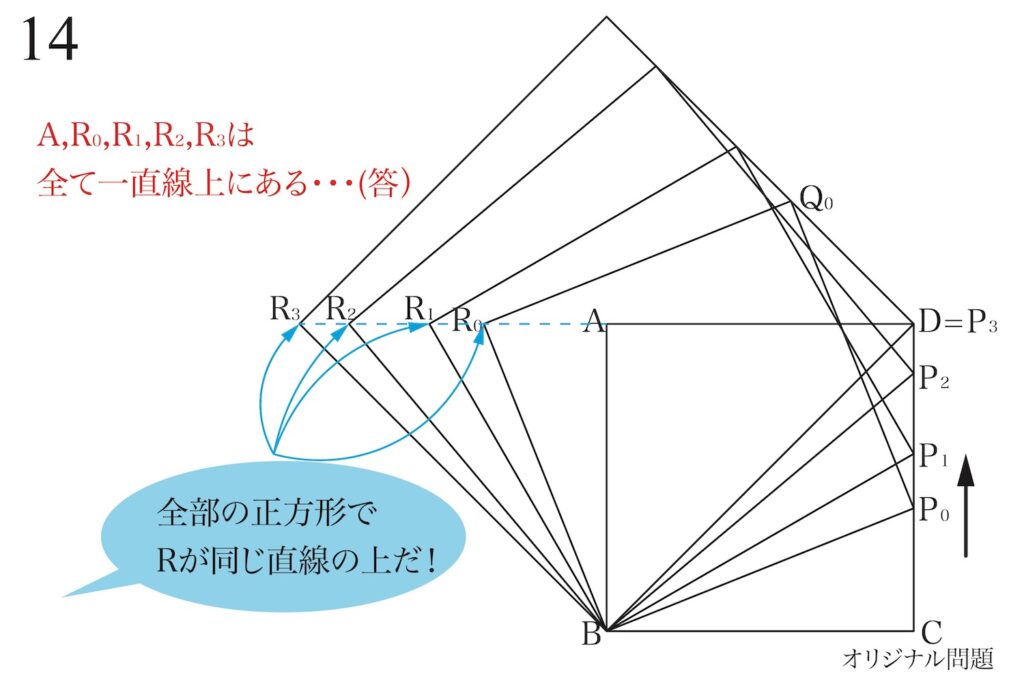

(2)のもう一つの答えは、「点A、点R0、R1、R2、R3は全て(同一)の一直線上にある」です。



これは
なかなか気づかないけど・・・



この線は
真横な気もする・・・



真横とか真上の方向だったら
気付きやすいかもね・・・
(2)の問題は「気づいた性質2つを答える」なので、上の二つが答えです。
・点D、Q0、Q1、Q2、Q3は全て(同一)の一直線上にある
・点A、点R0、R1、R2、R3は全て(同一)の一直線上にある
他にも共通する性質があるかもしれませんが、最も分かり易いのがこの二つでしょう。
点の名前の付け方は自由です。
Q0、Q1などとせずに、新たにX,Y・・・などと名前をつけても良いでしょう。
今回のようにたくさんの点が登場するときは、「点に添字をつける」と分かり易いです。



確かに
そうだね!



添字が同じ点は
「仲間」だから分かり易いね!
移動する点と新たに出来る図形を考える時は「同じ仲間・グループの点は同じ添字」が分かり易いです。
・移動する元の点の名前に添字をつけて整理
・同じ添字の図形は「同じ動く点に対する点」という同じ仲間・グループ
正方形の作り方:平行移動と90度回転

ここで、正方形がどのように出来てゆくかを考えてみましょう。
正三角形を作るとき、「一つの辺を60度回転」と考えました。
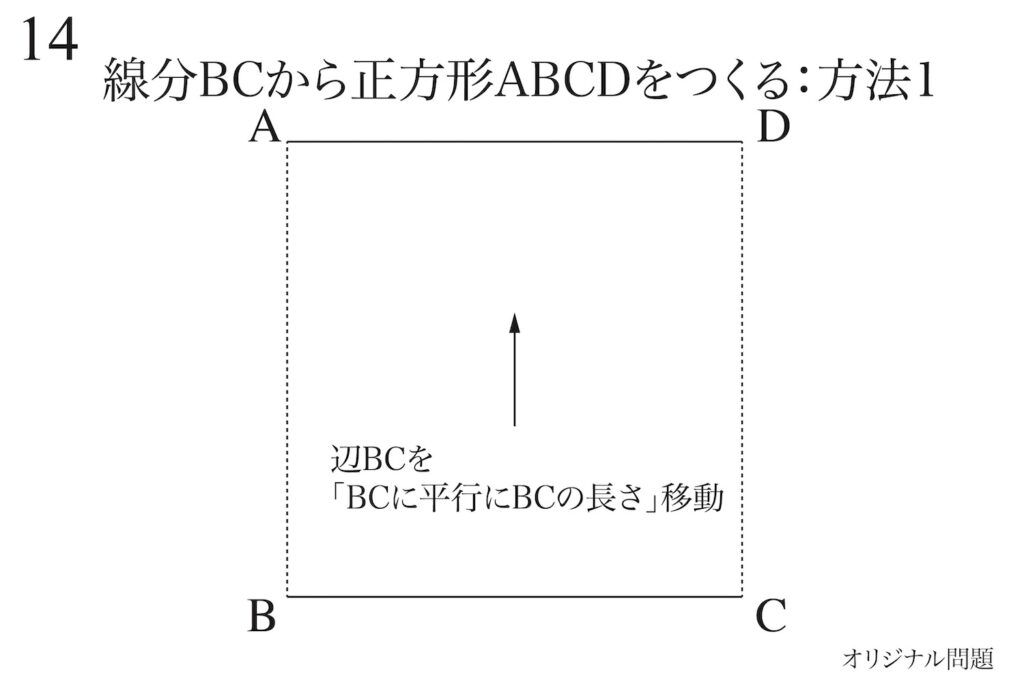

まず最初にオーソドックスな正方形の作り方「方法1」を確認しましょう。

一辺を「その辺と同じ長さ」平行移動すれば、正方形を作ることができます。
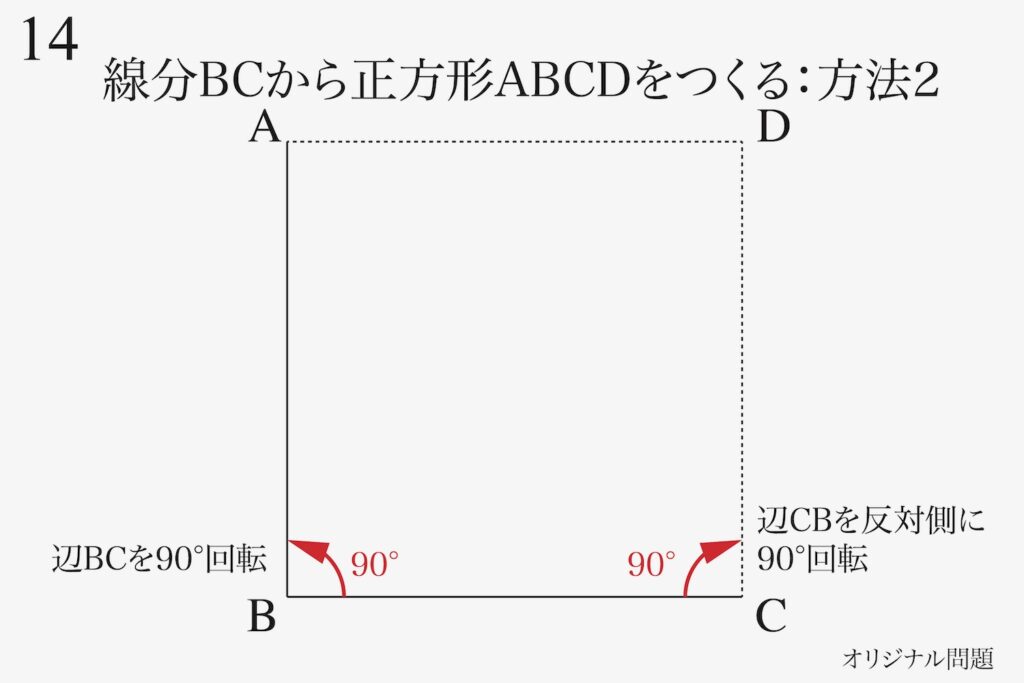

今度はもう一つの方法の「辺を90度、反対側に90度回転する」方法2を考えましょう。
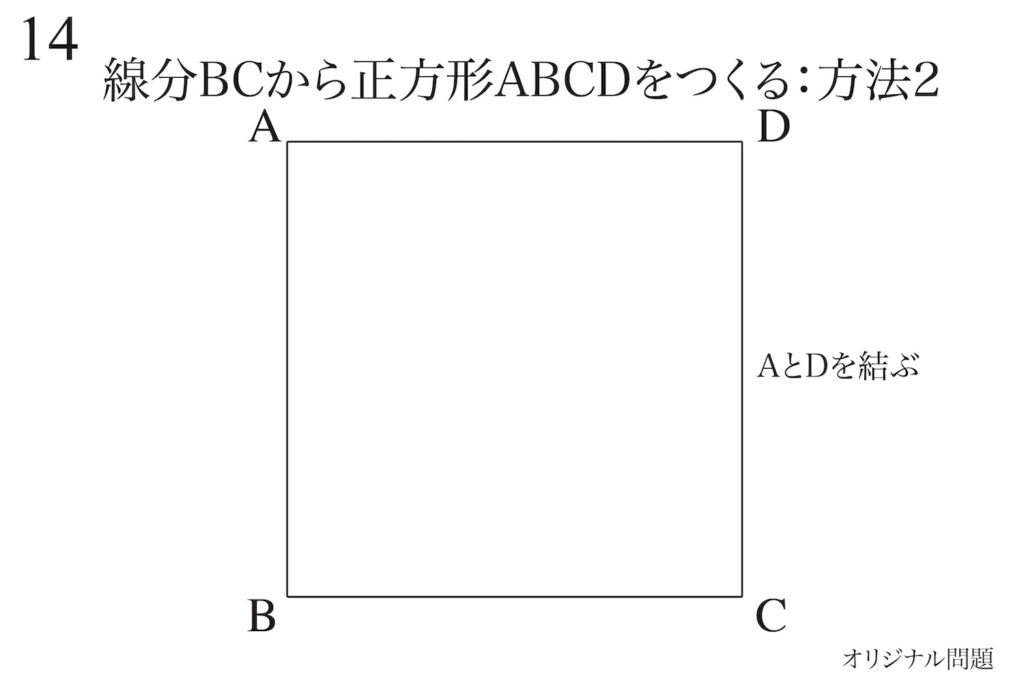

90度回転、反対側に90度回転(-90度回転)すると正方形が作れます。
・全ての辺が同じ長さ
・全ての角が同じで直角
正〜角形は「辺の長さと角度が全て同じ」ですが、正方形は「全ての角が直角」であることが大きな特徴です。
正三角形の「60度回転」と同様に、正方形の「90度回転」も知っておくと良いでしょう。
図形の性質の理由:矢印の考え方
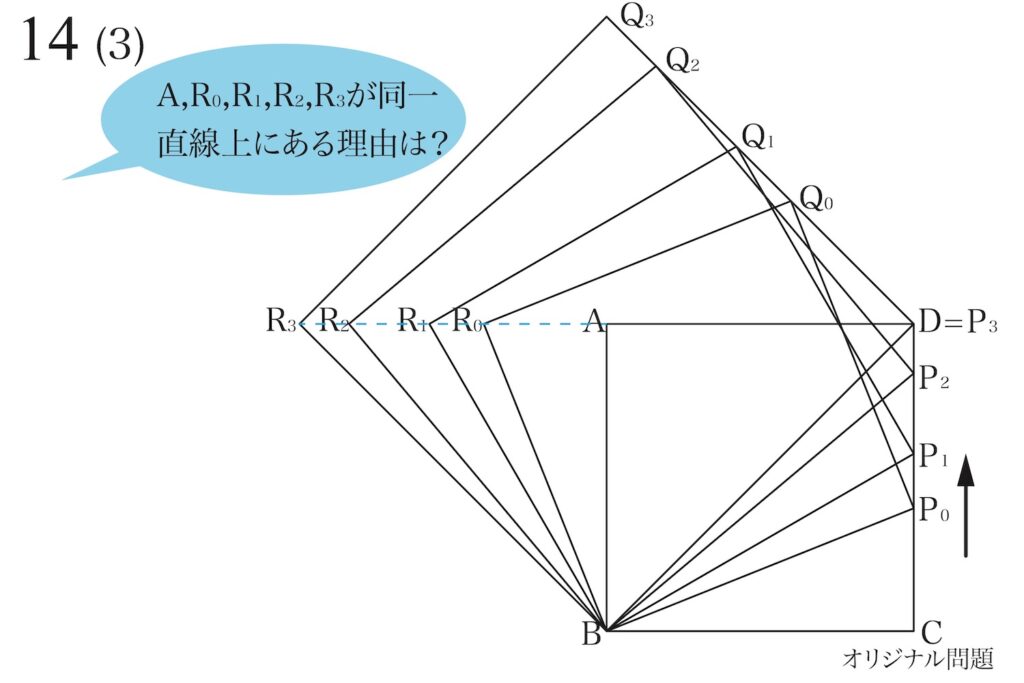

二つの性質が分かったので、(3)の「これらの性質を説明」を考えてみましょう。
二つの性質では、「Qの動き」の方が「Rの動き」よりも分かり易かったです。
「説明する」のは、「Qの動き」より「Rの動き」の方が分かり易いので、先にこちらを考えます。
上で考えた通り、正方形は「一つの辺を90度回転」と考えましょう。
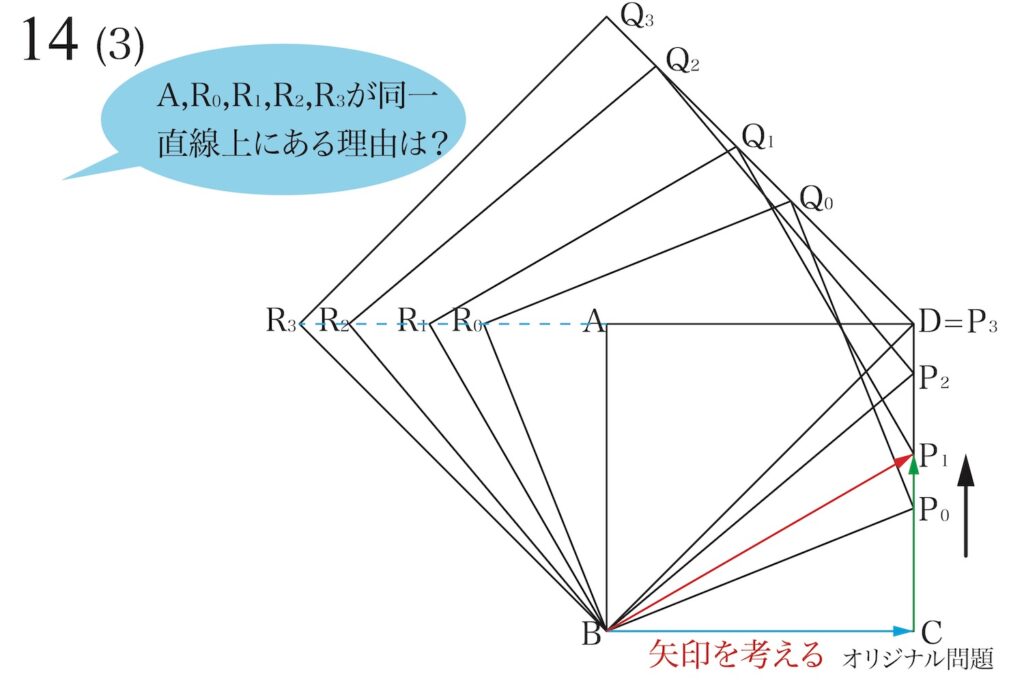

「動く点」の動きを追いかけるには、「矢印の考え方」が良いです。
例えば、動く点P1を矢印で考えましょう。
上の図のように、「BからP1の矢印=BからCの矢印+CからP1の矢印」となります。
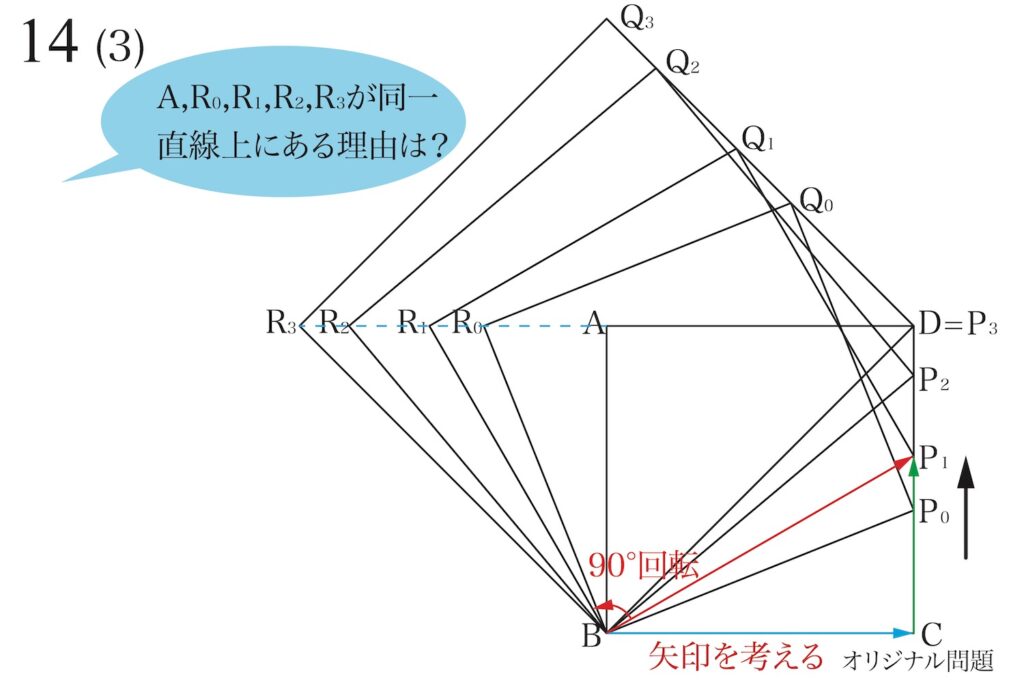

点P1に対応する正方形は「辺BP1を90°回転」すれば出来るはずなので、回転しましょう。
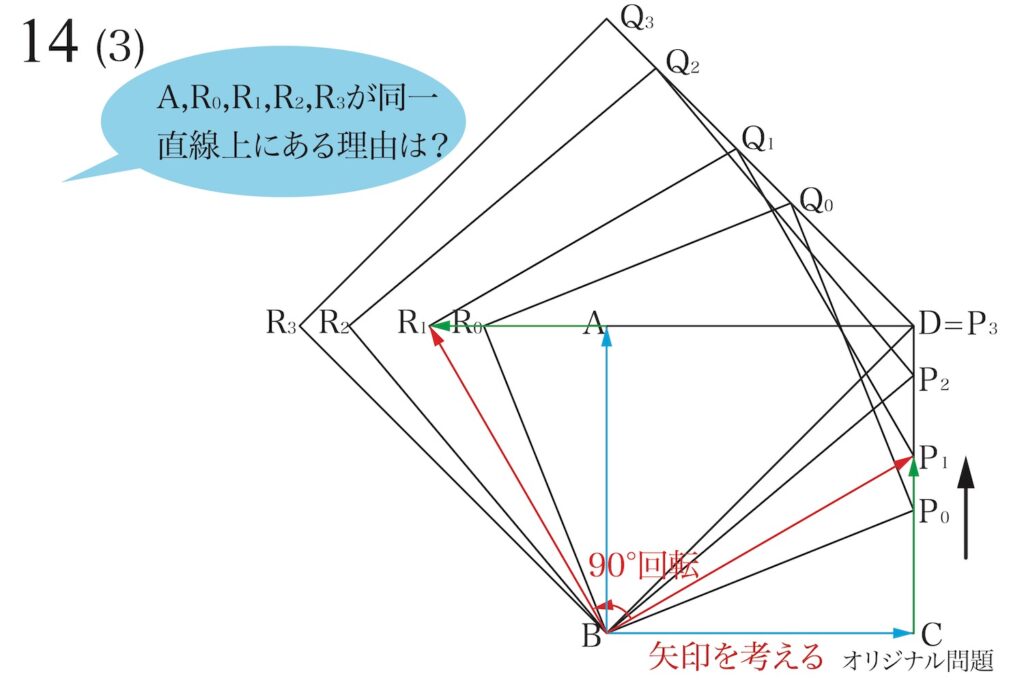

これで、先ほどの「正方形の作り方2」と同様に、正方形R1BP1Q1のもう一辺である辺BR1が完成しました。



これは
分かり易いね!



点Rの動きが
よくわかる!
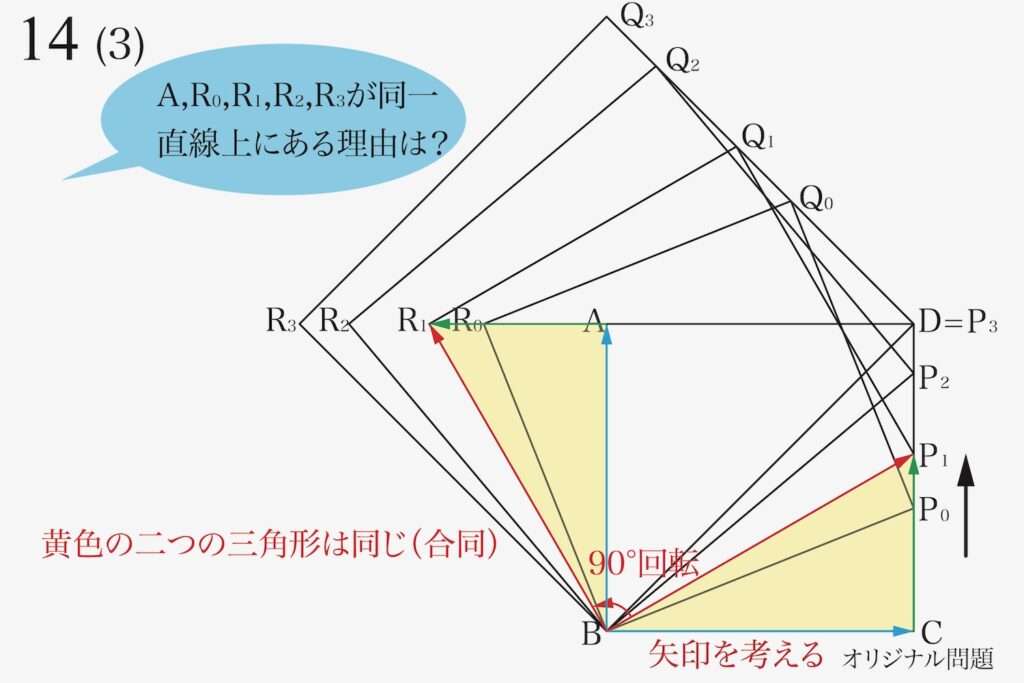

上の黄色の二つの三角形は「回転させただけ」なので同じ(合同)です。
先ほど、辺BP1を回転して、辺BR1を回転しました。
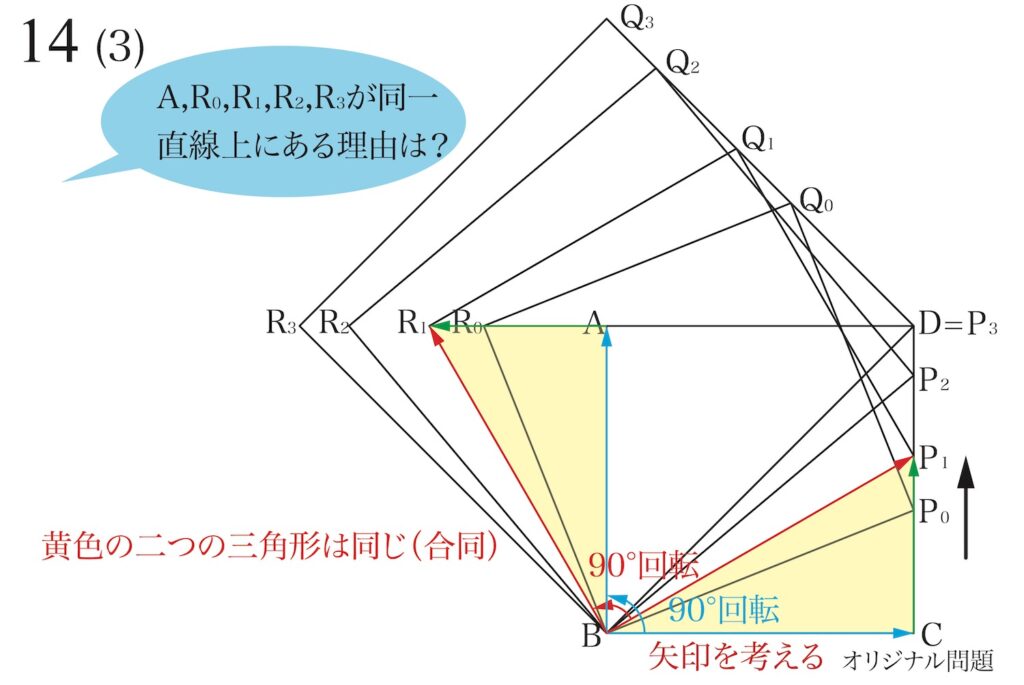

「黄色の三角形を90度回転している」ので、辺BCを90度回転すると辺ABとなります。
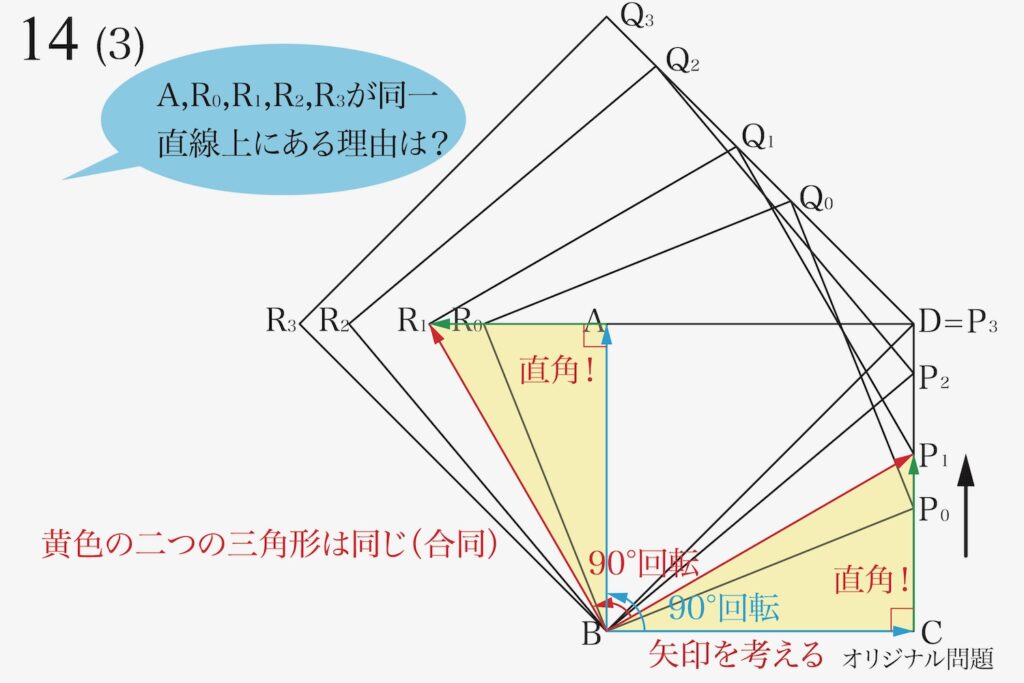

二つの黄色の三角形は、同じ(合同の)直角三角形です。
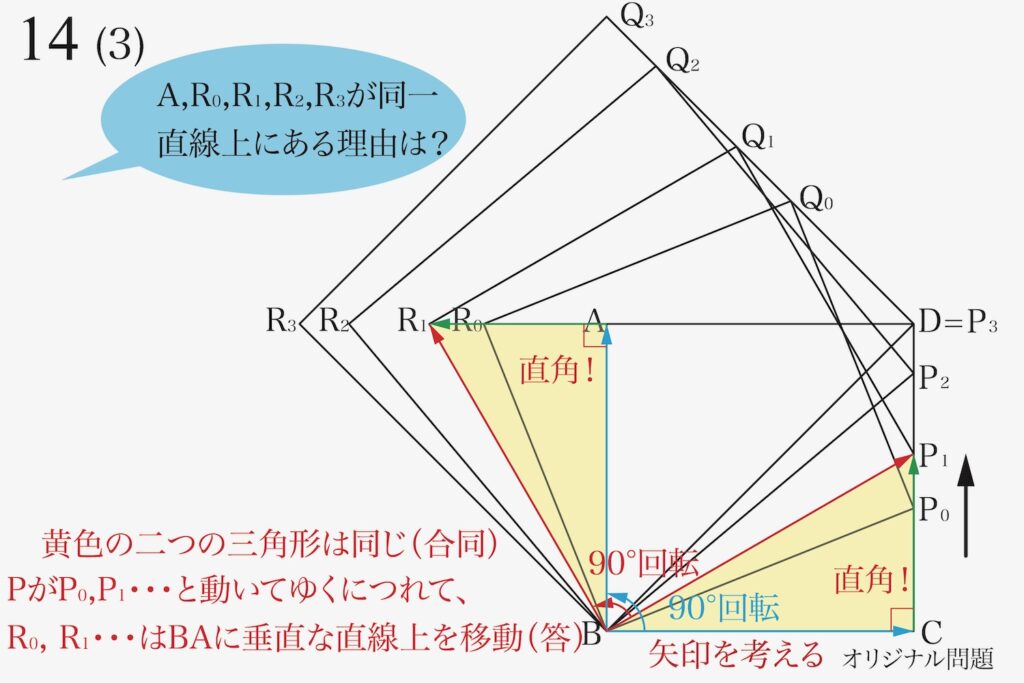

そこで、上のように「点PがP0,P1,P2,P3と移動するにつれて、R0,R1,R2,R3はBAに垂直な直線上を移動」します。
(3)の「説明」に関しては「証明」のように厳密ではなくても、上のように説明できることが求められます。
・「点D、Q0、Q1、Q2、Q3は全て(同一)の一直線上にある」説明←こちらの説明は?
・「点A、点R0、R1、R2、R3は全て(同一)の一直線上にある」説明←こちらを説明
(3)の答えの後半部の説明が終わりました。
前半部も「矢印」を元に考えて説明してみましょう。
今回説明した内容よりも少し難しいですが、次回ご紹介します。
次回は下記リンクです。




