前回は「図形を算数的に考えるコツ・ポイント〜異なる説明をする大事さ・自分で思考する学び・「〜ではない」状況を具体的に考える・角度に注目・図形を作る辺は「長さと角度」が大事・問題 13(3)解法〜」の話でした。
問題 13
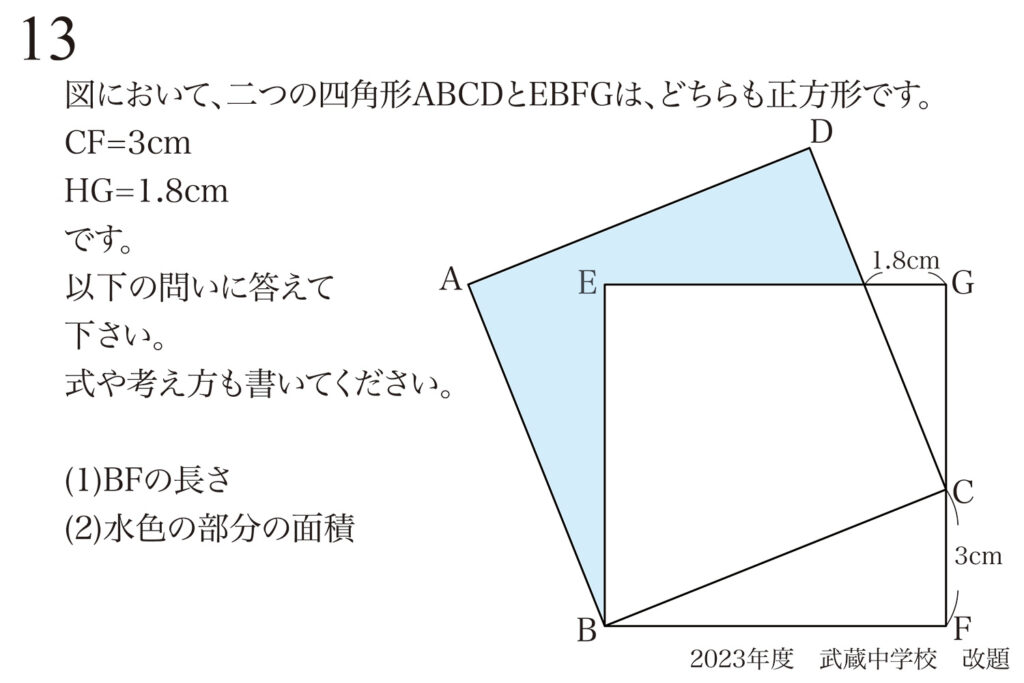
全体を見渡して見えてくる解く鍵
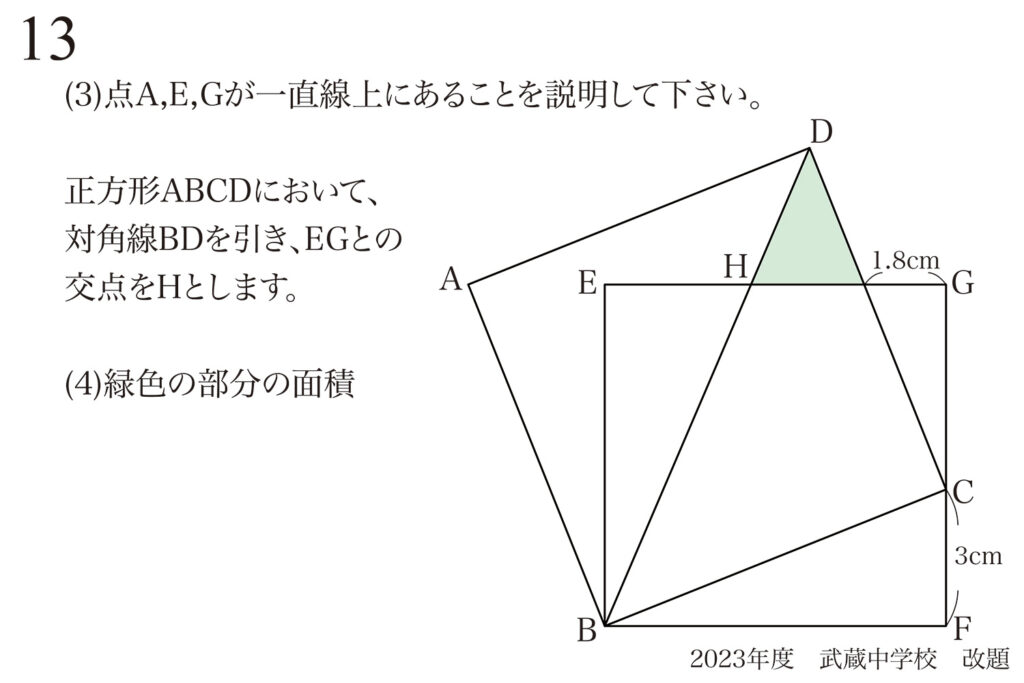
緑色の部分の面積を求めましょう。
(4)の問題である「緑色の部分の面積」を求めるにあたり、大事なことがあります。
それは、まずは「これまでわかった状況」を整理する・俯瞰する姿勢です。
・問題の条件を全て描きこむ:同じ長さ・同じ角度など
・図形の性質などを描く過程で、条件を頭で整理するので解きやすくなる
 男子小学生
男子小学生でも、
問題解かなきゃ、って気が焦るよ・・・
このように図形でも何でも、本試験・模試の際に、焦ってしまいがちな算数(数学)。
他の科目も焦ったり、「一秒でも早く」という気持ちになるかもしれません。
特に算数(数学)は、その傾向があります。
それは、



解法・解くきっかけが、
分かれば一気に進むのに・・・
このように「焦る気持ち」になるからでしょう。
他の理科・社会・国語等では、「一気に進む」ということは少ないです。
一方で、「解法の鍵」が分かれば一気に進むことが多い算数(数学)。
「解法の鍵」が見つからないと、「迷路に入ってしまう」気持ちになります。
1.最後の問題のみだと難しいため、ヒントを作って解きやすくする
2.問題を分け、出来る部分を明確にして、採点の際に点数の差が出やすくする
今回は、小問が4つに分かれています。
前までの(1)〜(3)で分かったことや考えたことを使う可能性が大きいので、それも考えましょう。
そのためには、最初は「全体を見渡す」俯瞰する姿勢が大事です。
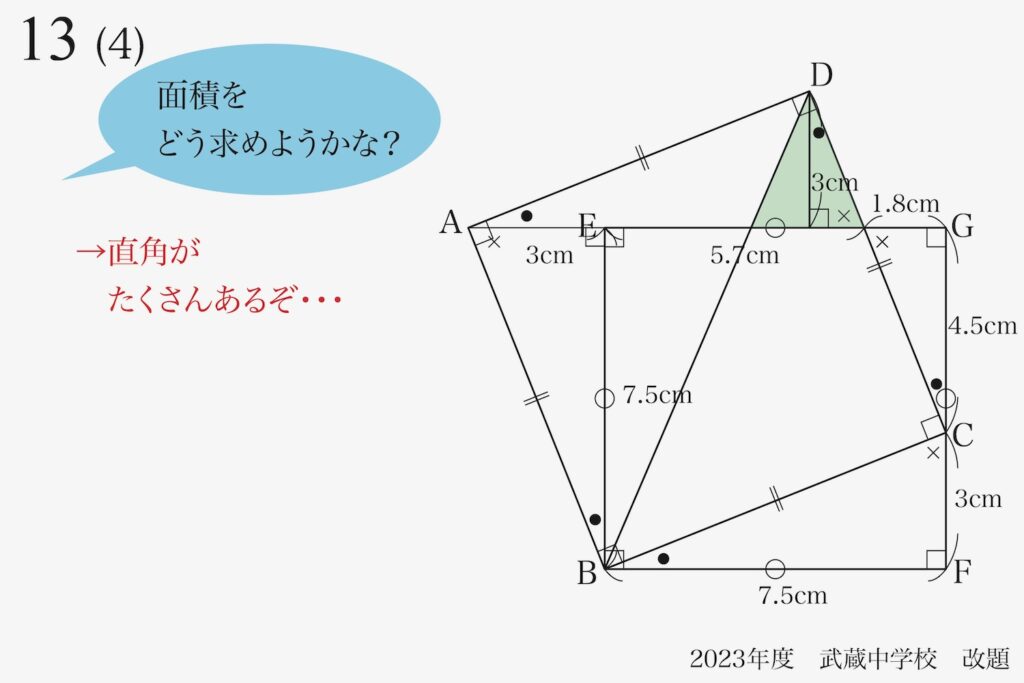

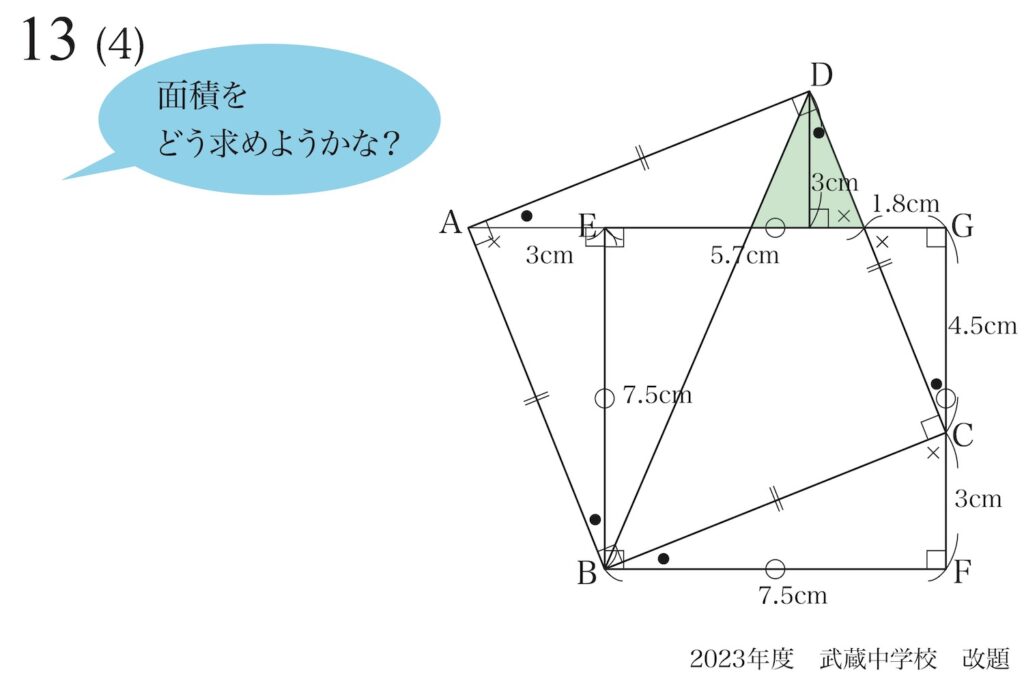
ここで、「これまでわかったこと」を描いて、全体を見渡してみましょう。
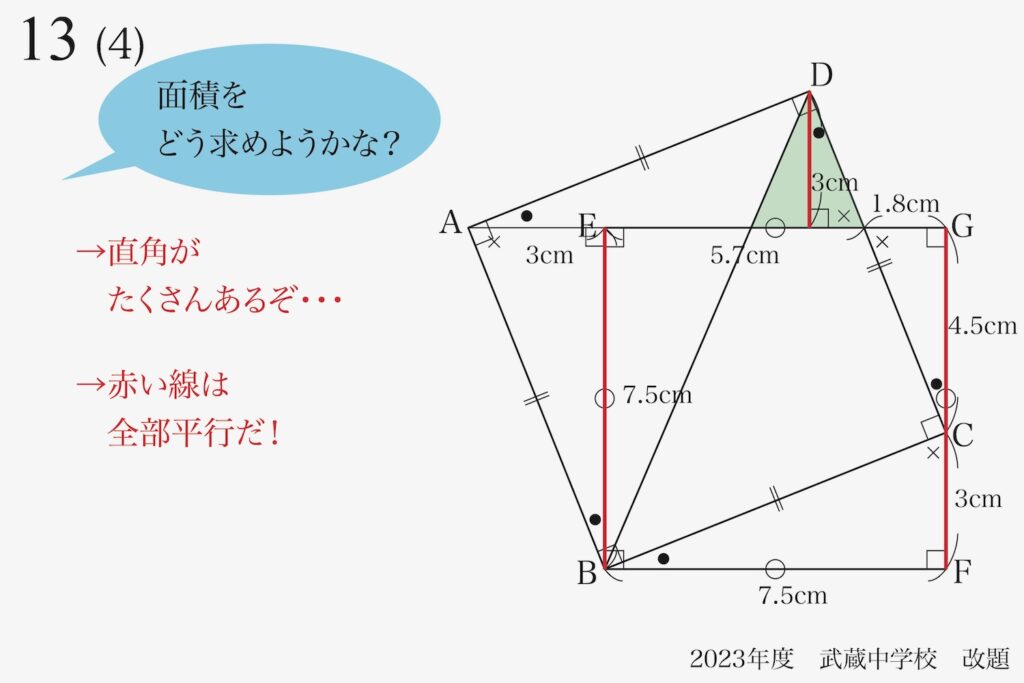
直角が、たくさんあります。
・180度から直角を引くと直角:180-90=90
・直角は同一角度が見つけやすい→相似形が見つかりやすい
これは、「正方形が二つ」ある時点で、直角が「4個 x 2 = 8個」あるので、



直角が沢山あるのは
当たり前だけど・・・
「正方形の上は直角は当たり前」と考えるかもしれません。
問題を解くプロセスにおいて、AE・DからEGへの垂線(垂直な線)など、さらに直角が見えます。



うん。
たくさん直角がある!
そして、この図形全体をじっと見てみましょう。
手を動かしても良いですし、頭の中でイメージしても良いです。
次にすることは、何でしょうか?



相似形を
探すことだよ!
・相似形を探す
・「同じくらいの大きさ」の相似形の時、「同じ(合同)図形」かどうか考える
相似形を発見するコツ・ポイント:同じ角度を探す

「相似形」を見つけることが大きな鍵になることが多い図形問題。



相似形は
どこだ?
「相似形を探そう」と気持ちが逸ります。
確かに「相似形が見つかる=解く鍵」であることが多い、図形問題。
・ある形AとBが「相似」
→片方の図形を拡大・縮小すれば、もう一方の図形となる
・相似の条件
←→対応する角度が同一
←→対応する辺の比が同一
「相似形を見つける」プロセスにおいて、「良い補助線を見つける=解く鍵」になる傾向があります。
「直角が多い」ということは、ある線に対して「直角となる線が多い」ということになります。
上の図で、赤い線は全てが「直線AGに対して直角」となります。
・辺は「長さと角度」で決まる
・それらの辺が「どのようにつながっているか」を考える
図形問題は「長さ」ばかりではなく、「角度」に注目すると視野が広がるでしょう。
上の図で「赤い線は全て平行」となります。



平行な線があると、
相似形が沢山あるね!
相似形と相似比
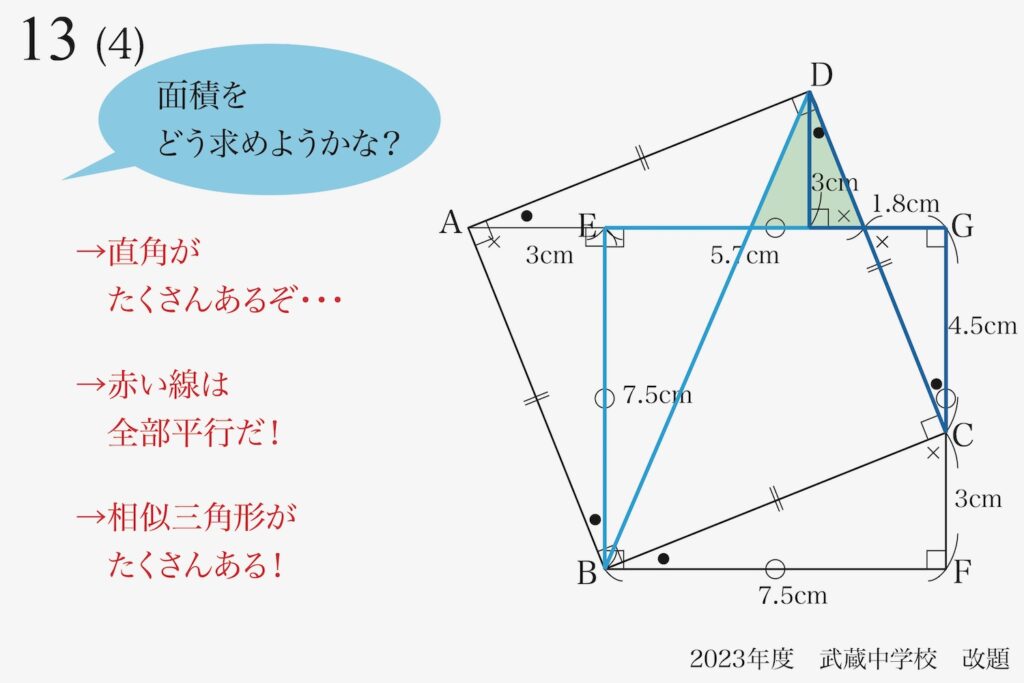

二組の相似形が見えてきました。
しかも「それぞれの相似形の辺の長さが、たくさん分かる」状況です。



これで、
一気に進められる!
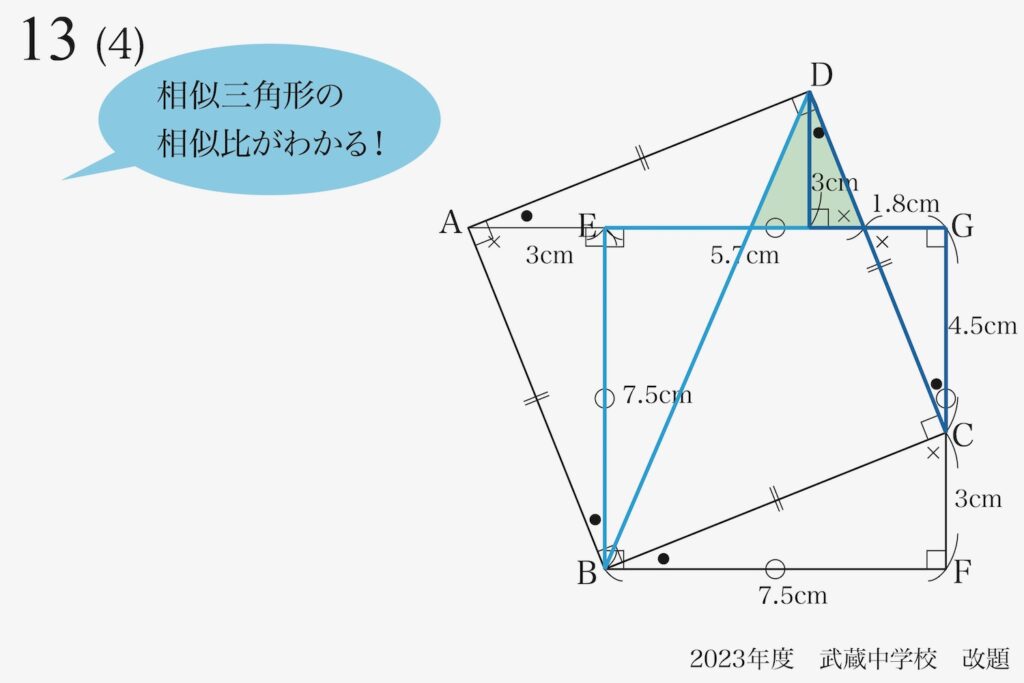

具体的に相似比を考えてみましょう。
これらの相似形の対応する辺の長さが分かるので、考えてみましましょう。
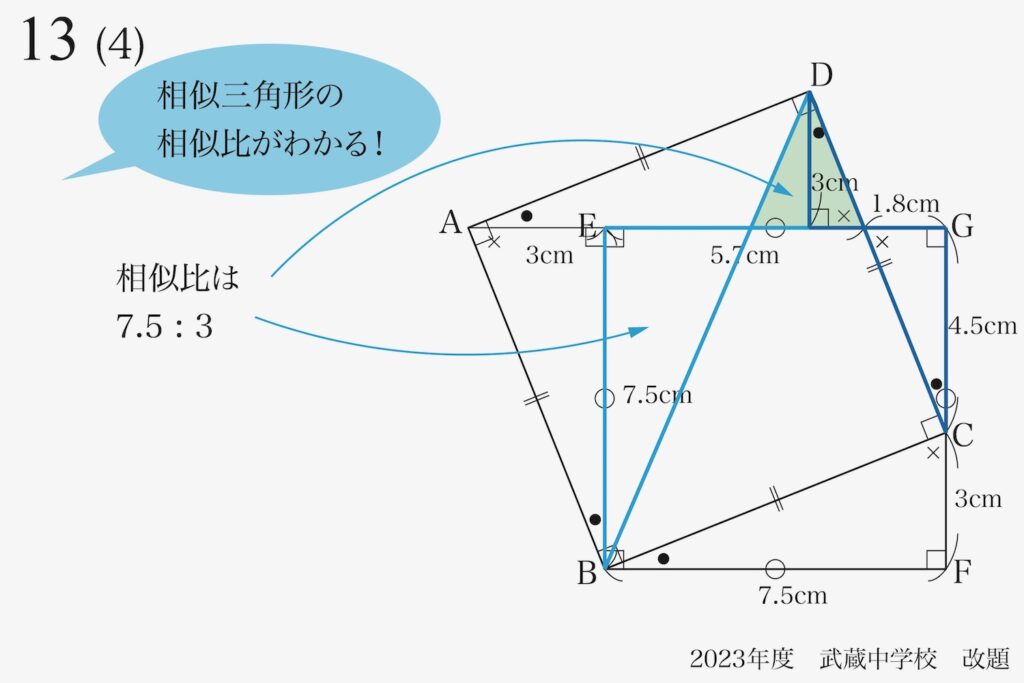

左側の水色の線の二組の相似形の相似比は、「7.5 : 3」です。
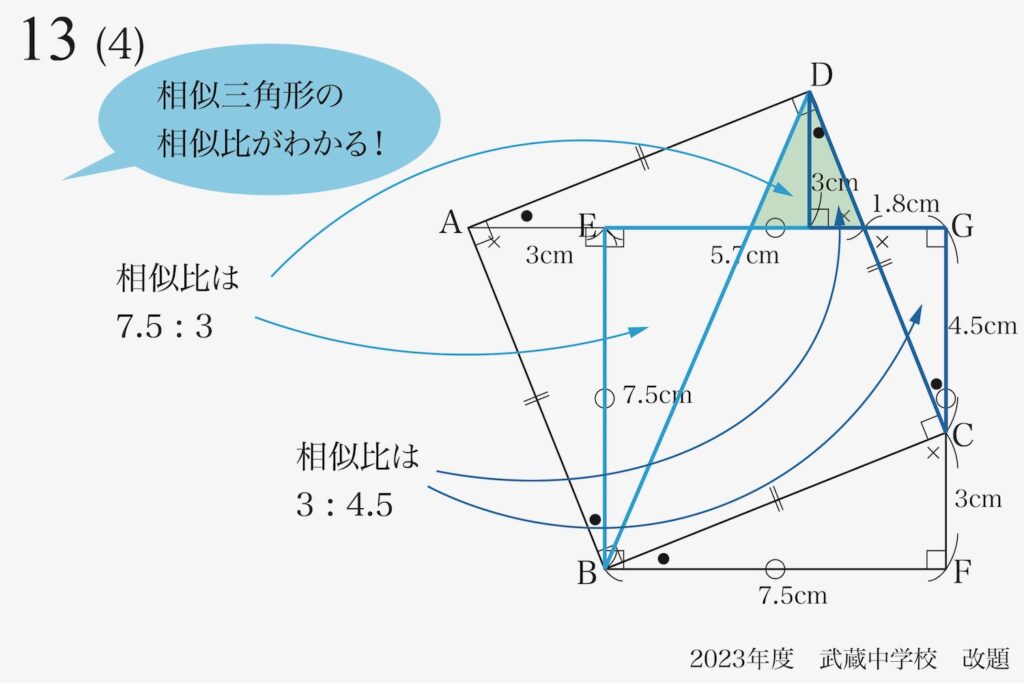

右側の水色の線の二組の相似形の相似比は、「3 : 4.5」です。
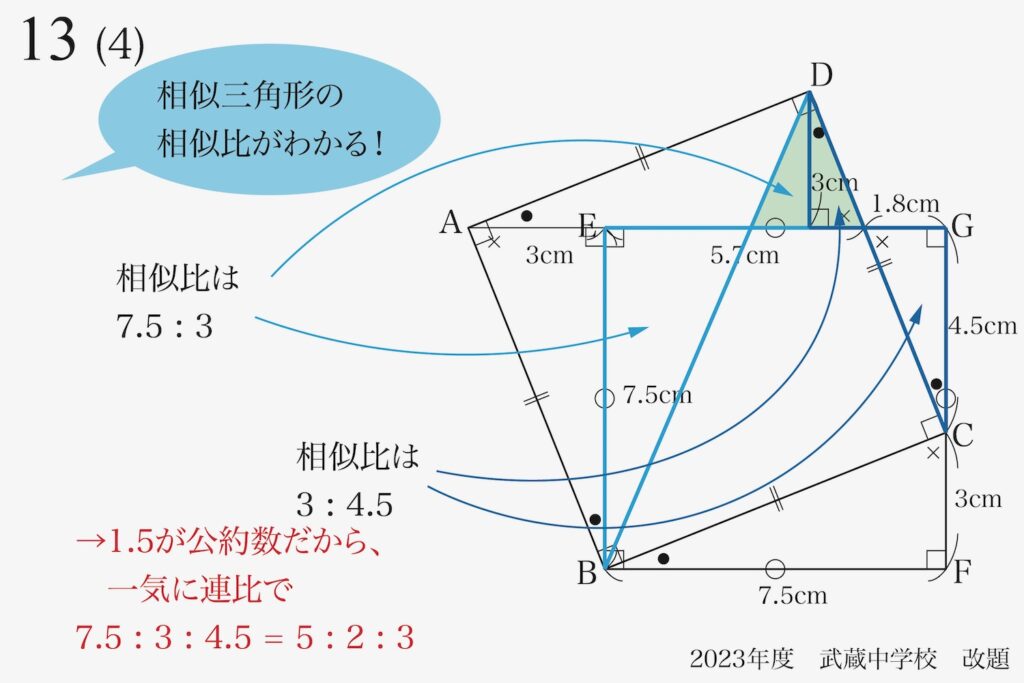

これで、それぞれの三角形の相似比がわかり、さらに「1.5が公約数」です。
「7.5 : 3」と「3 : 4.5」の関係があるので、一気に「7.5 : 3 : 4.5 =5 : 2 : 3」です。
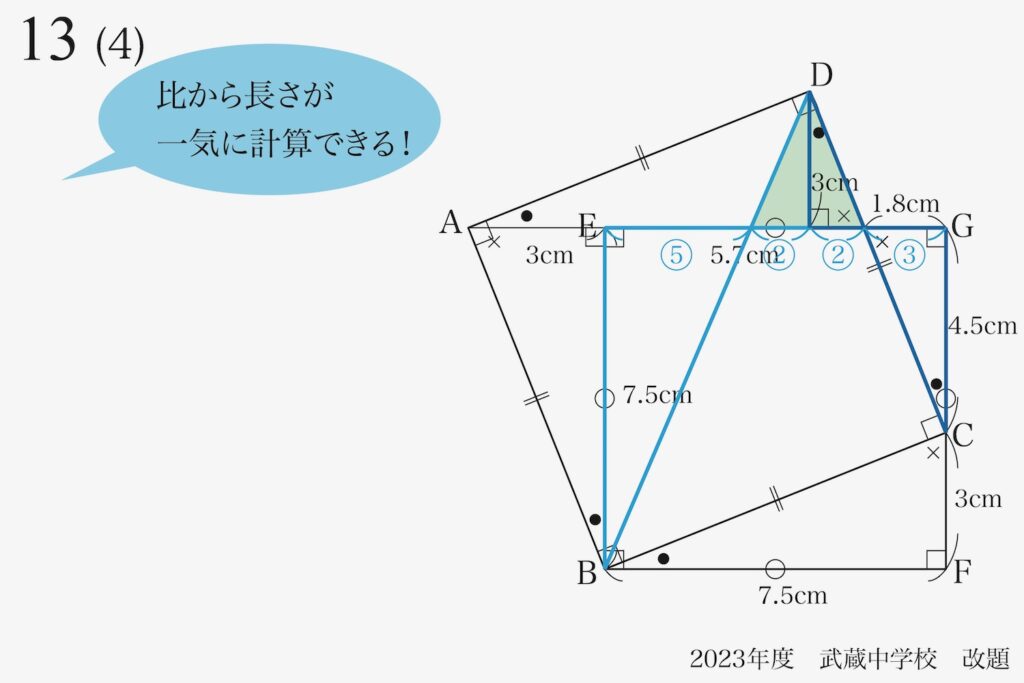

これで、辺の比が連比で一気に求まり、進められます。
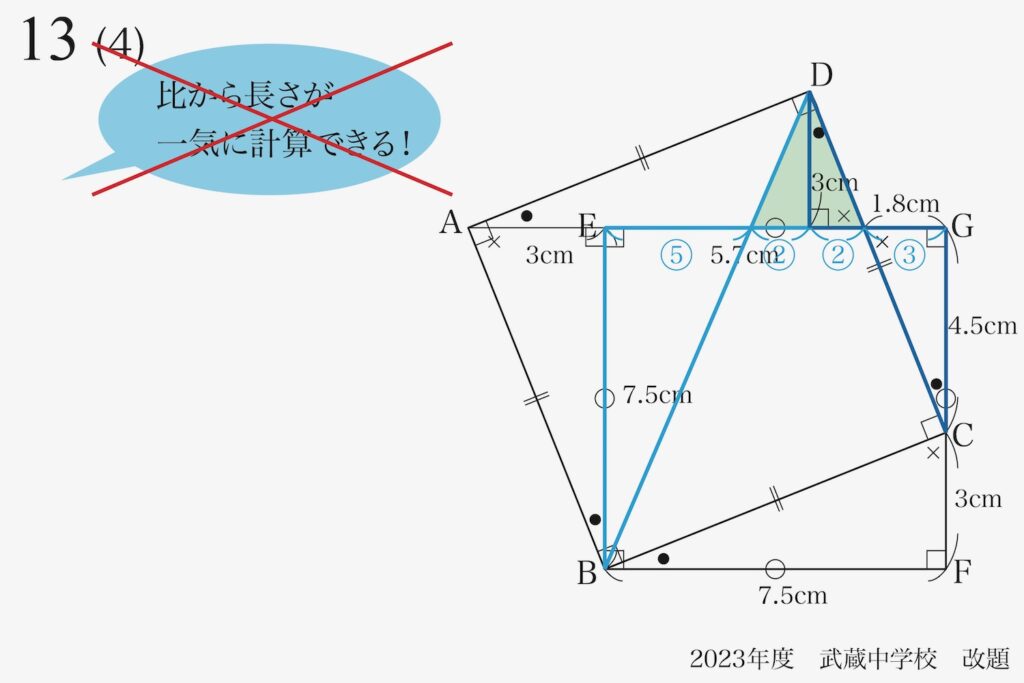

ちょっと待ってください。
これは「間違った考え方」です。



えっ、
なぜなの?
もう一度、相似を考えてみましょう。
そして、「どこが間違っているのか?」を考えてみましょう。
相似形の条件をもう一度復習しながら、自分の手で描いて考えてみると力がつきます。
「どこが間違っているのか?」を「全体を見渡して」しっかり考えてみましょう。
次回は下記リンクです。



