前回は「二つの正方形と図形問題を得意になるコツ・ポイント〜図形の性質を理解・早めに過去問と入試問題と向き合う大事さ・目標を理解して合格へ大きく前進・問題 13〜」の話でした。
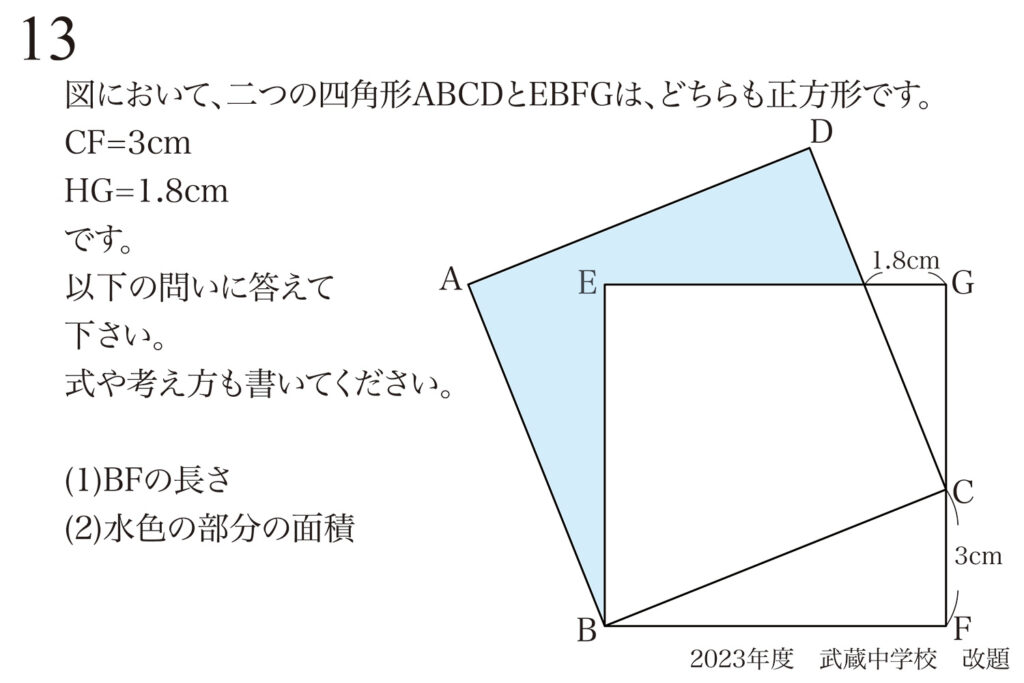
問題 13
学力を高める姿勢:テクニックやパターンと「考え方の骨格」
 男子小学生
男子小学生正方形は分かりやすいけど、
二つあって、斜めだから・・・



形は分かるけど、
なんとなく難しい・・・
正方形は「辺が水平・垂直」だと理解しやすいです。
問題13では「一つの正方形が斜め」になっているのが、難しく感じる理由かもしれません。
そのため、難しく感じる方が多いかもしれません。
「問題の解き方」と共に「学力を高める」学び方の具体的姿勢の話をご紹介します。
中学受験の図形問題ですが、考え方は高校受験・大学受験の数学も共通する点があります。
中学受験〜大学受験の算数・数学において、非常に多岐にわたる分野があります。
中学受験では、図形(平面・立体)・てんびん算・旅人算・ニュートン算・つるかめ算・・・・・
主だった分野・単元だけで、数え方によりますが20〜30程度になるでしょう。



ニュートン算とか
面積算は得意だけど・・・
さらにそれぞれの分野において、「考え方」や「テクニック」があります。



これを全部
学ばなければならない・・・



解法やテクニックは
全部頭に入れなきゃならないんだね・・・
受験生は、とても大変です。
それぞれの分野では、非常に多くの「考え方」や「テクニック」があります。
戦後、日本が高度成長を続け、中学受験〜大学受験が加熱してきたのが1970年代〜1980年代。
それから40年以上の時間が経過しました。
高度成長期の「輝いていた日本」の話を、上記リンクでご紹介しています。
その間、実に多種多様な問題が出題されました。
近い未来に受験する中学受験生〜大学受験生で「1980年代の過去問をやる」方は極めて少ないでしょう。



どこで、そんな昔の
過去問を手に入れられるの?
神保町などの古書店には「昔の過去問」があります。
過去問は早めにやったほうが良いですが、「数多くやれば良い」わけでもないです。
それよりも大事なことは、一題一題をしっかり理解しましょう。
この40年以上の膨大な蓄積がある中、出題者側も一生懸命に工夫してきました。



この問題面白そうだけど、
類似した問題が他で出題されていないか・・・



これは新しい視点の問題で、良さそうだけど
どうだろう?
その「様々な工夫」が、「解法」と「テクニック」の多様性をもたらしているのです。
しっかり理解して一題から多くを学ぶ:応用力構築
そこで、「しっかり理解して一題を解く効果を高める」のがベストです。
図形問題は、非常にたくさんの問題があります。
高校受験〜大学受験は数多くの定理が出てくるので、一定の数の定理を頭に入れる必要があります。
対して、中学受験では「数多くの定理」は範囲外となります。
それにも関わらず、多様な問題が出題されます。
算数の全分野に共通することは「基本姿勢」をしっかり身につければ一気に解けるようになるです。
・各分野の基本的手法・考え方:問題を解きながら実践的に身につける
・各分野の応用的手法・考え方:一題一題しっかり学び、一題から多くを習得
今回の話は基本的姿勢で「算数が得意な方」は、



もう分かって
いるよ!
このように「分かっている」方もいらっしゃるでしょう。
問題13ではじっくりと考えてゆきます。
中堅校〜最難関校志望の幅広い方に、「しっかりした基本」を身につける参考にして下さい。
図形問題の基本的姿勢:相似形を探す
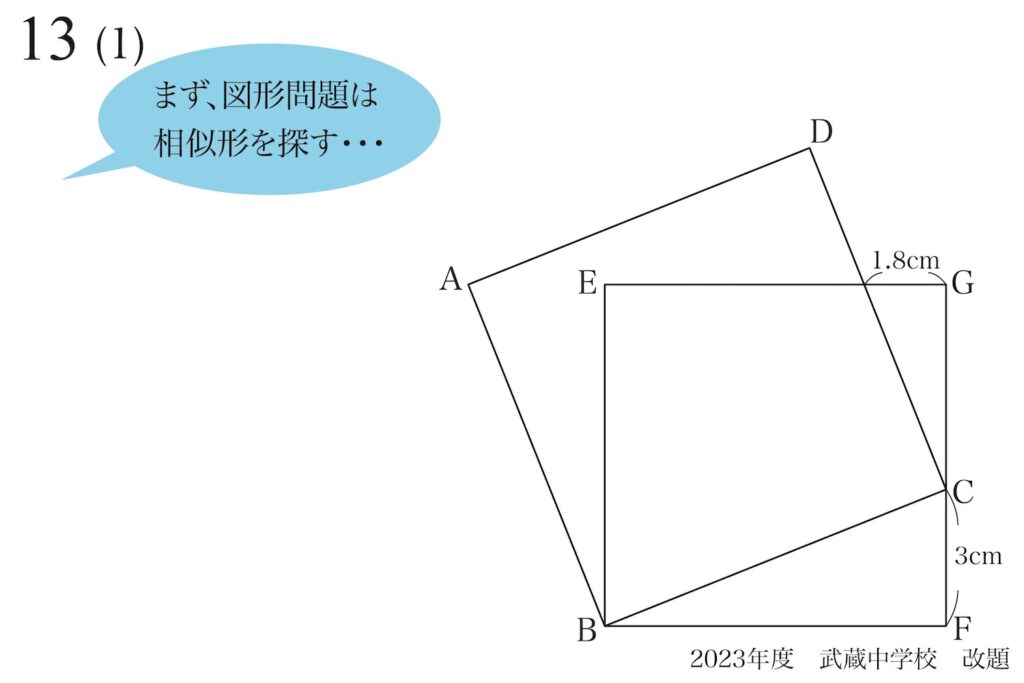

具体的に問題を考えてゆき、解いてゆきましょう。
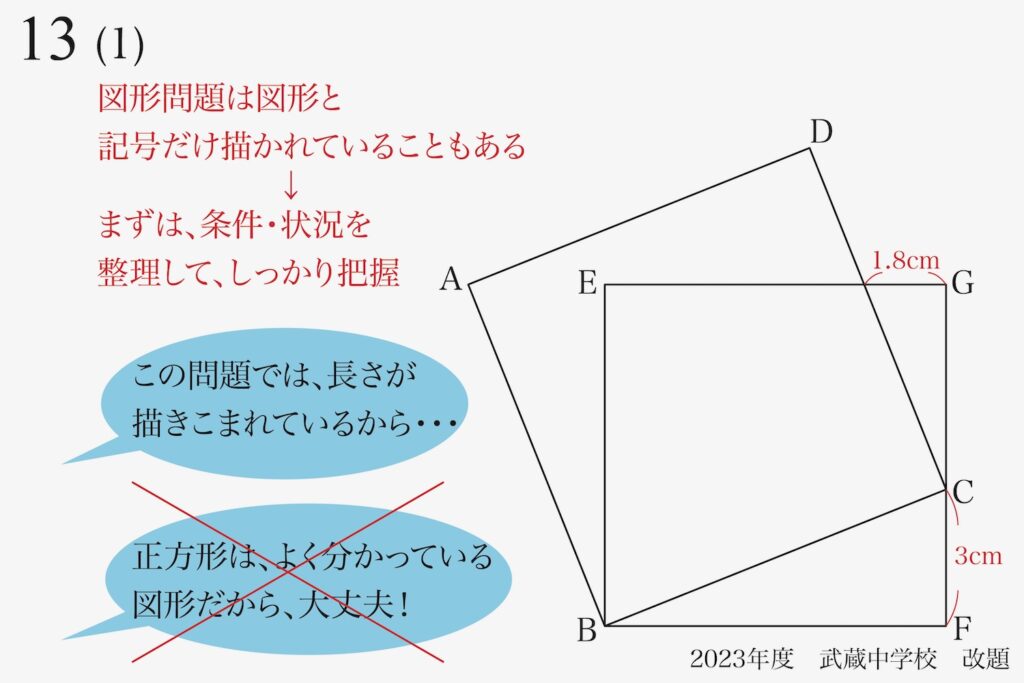
ポイントは「二つの図形は正方形」です。
そこで、「まず相似形」を考えます。
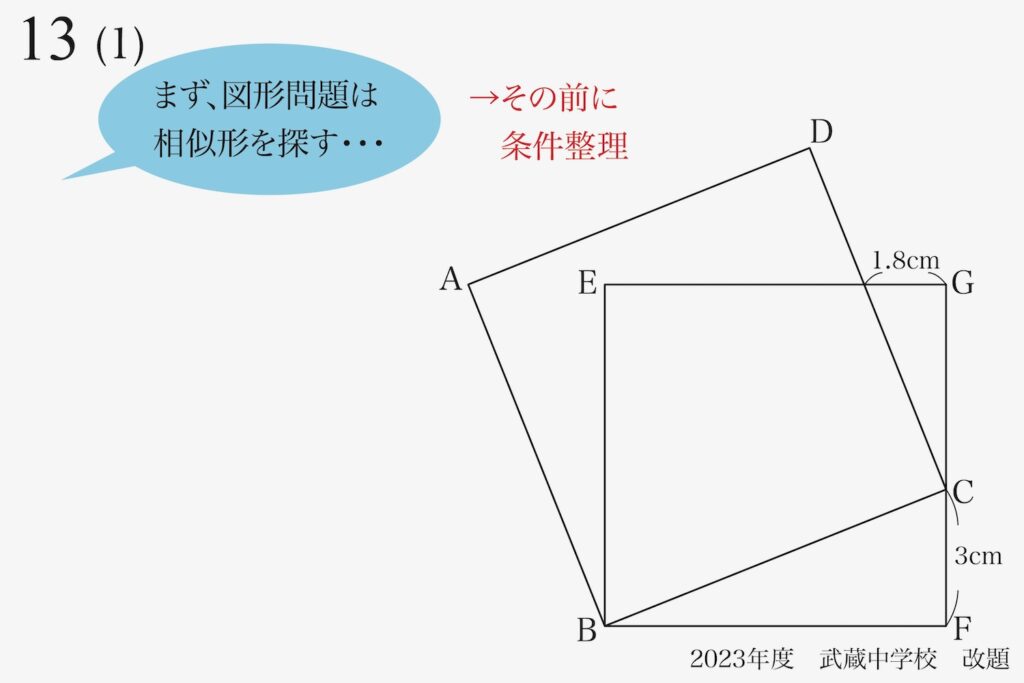

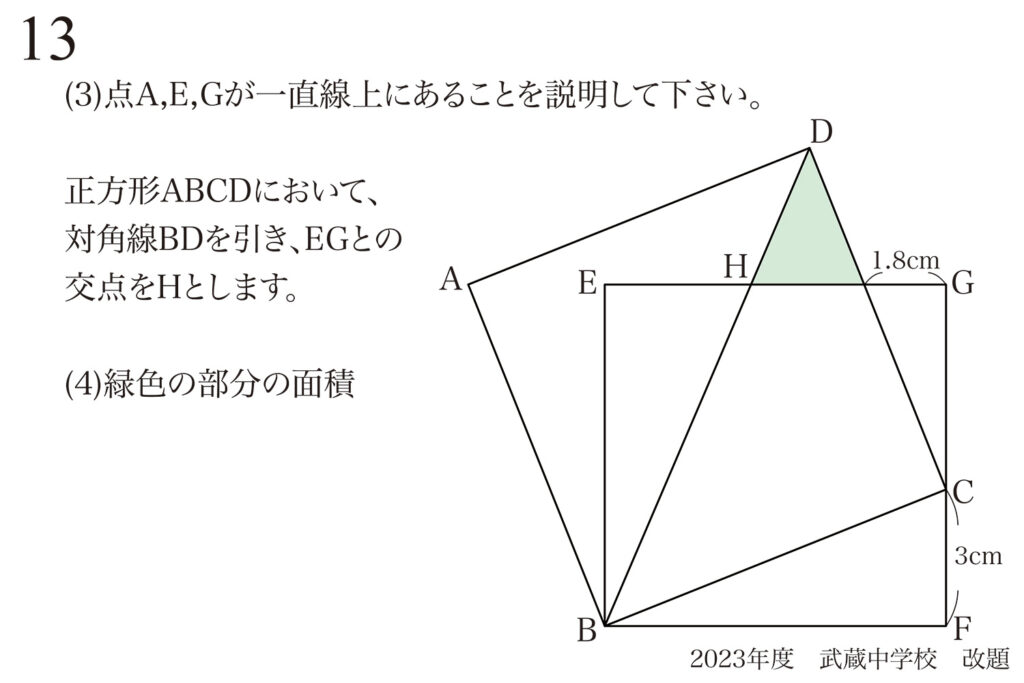
その前に、しっかりと条件を整理・理解することが最重要です。
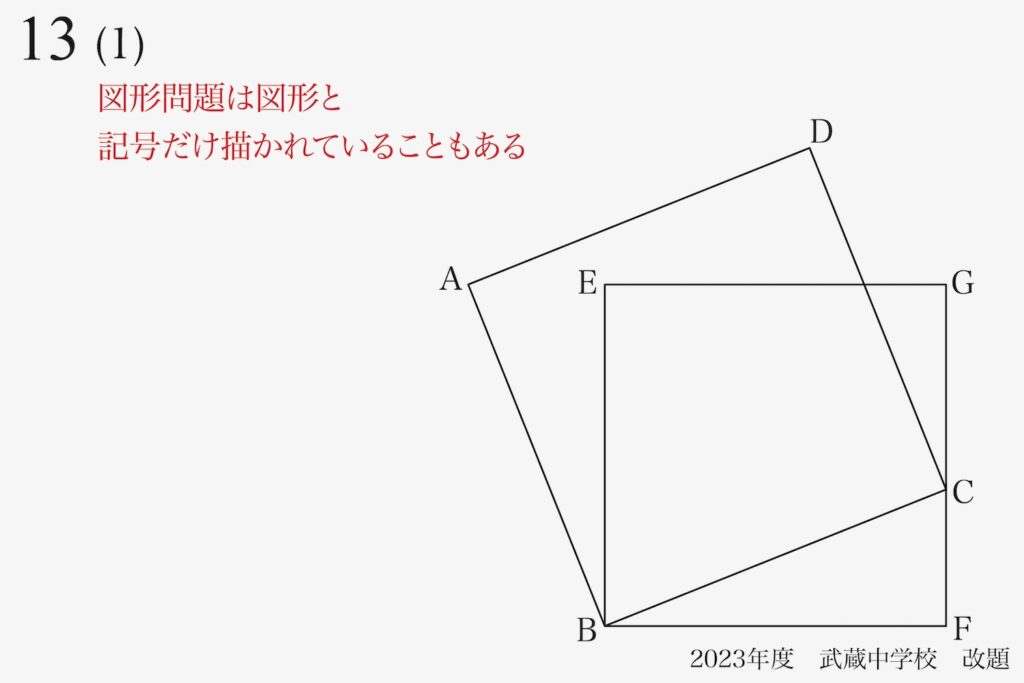

図形問題では、上記の通り図形・記号だけ描かれて「長さ等の情報は文章内」であることがあります。
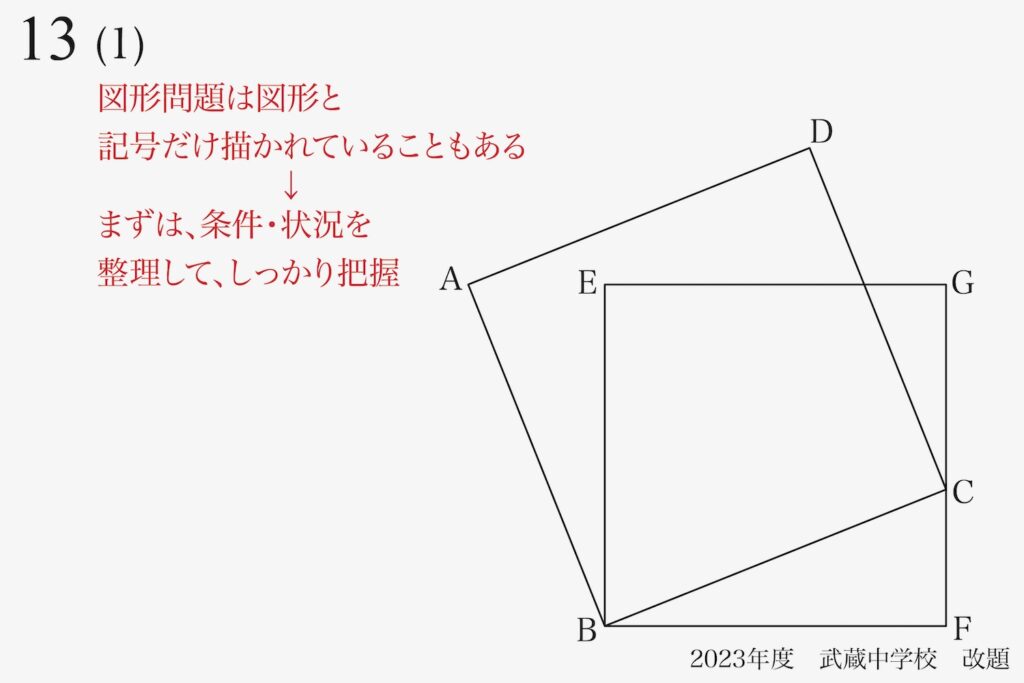

今回の問題は「長さが記入されている」状態ですが、「まずは条件・状況を整理・把握」しましょう。
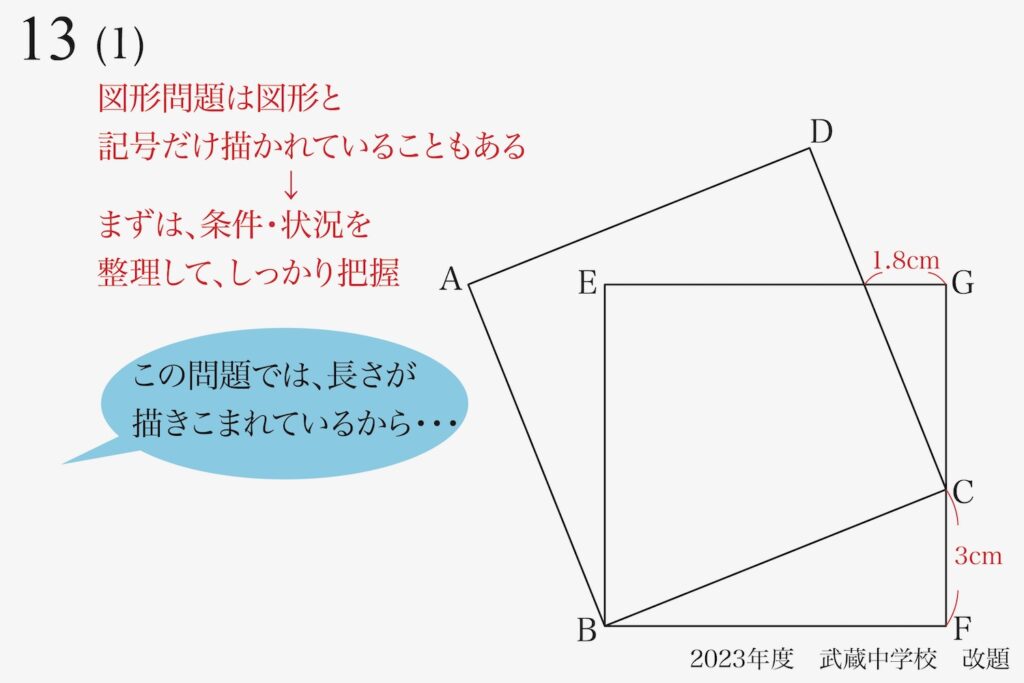

この問題では「長さの条件」が描きこまれています。
こういう「長さ・角度などの条件」を勘違いして、「自分で問題を難しくしてしまう」ことがあります。



そういえば、前の模試で
勘違いしたことある・・・
「勘違いで勝手に難しくする」はしないように、落ち着いて「しっかり理解」しましょう。
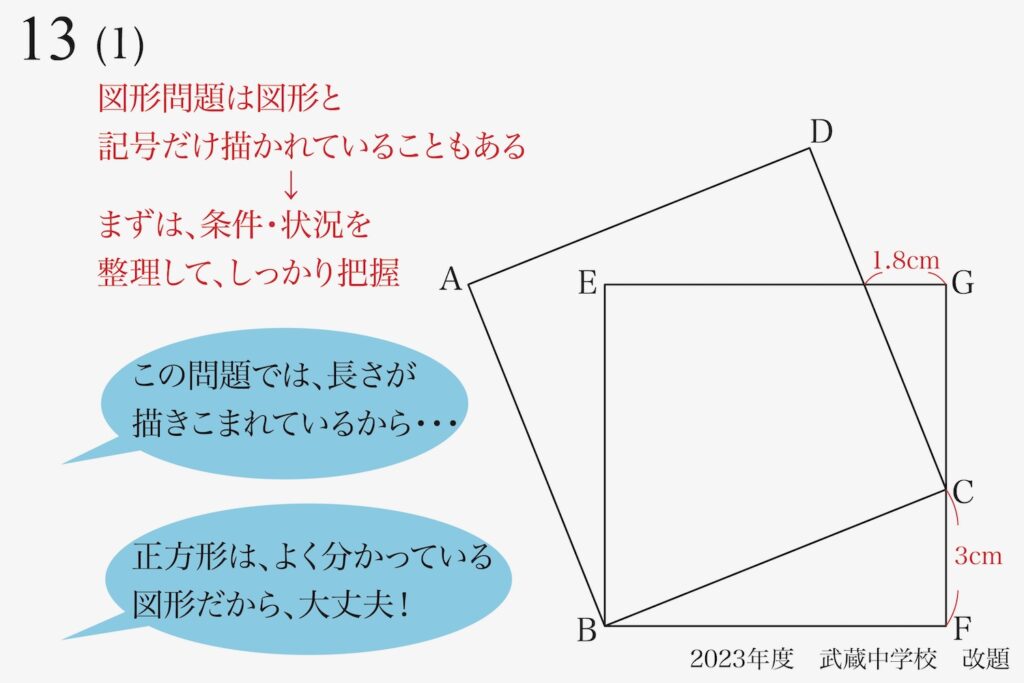

この問題は「長さが描きこまれている」ので、勘違いがない分「良心的」です。
そして、大きな条件である「二つの四角形が正方形」です。
ここで、「正方形」という図形は、「誰でも知っている簡単でシンプルな図形」です。
そこで、



正方形なら
分かっている!
このような方が多いかもしれません。

「よく分かっているから、大丈夫」は、よほど学力が上がるまではやめましょう。
特に算数の基礎を固めて、応用力を磨いてゆく段階で大事なこと。
それは「しっかり状況を描く」です。
「分かっていること」を描いて視覚化
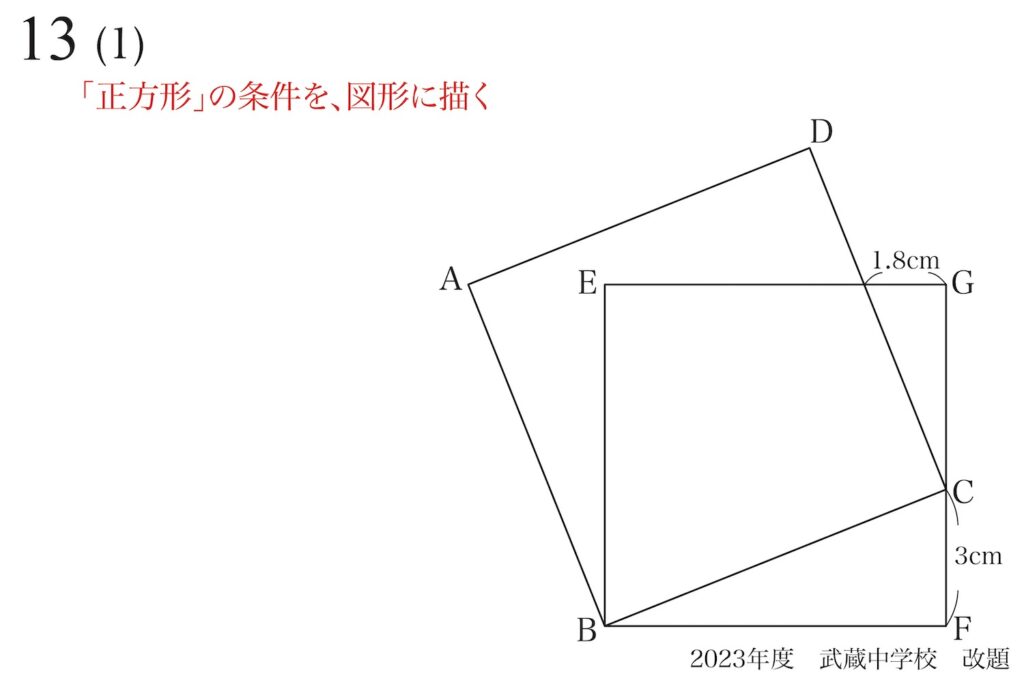

そこで、「正方形の条件」を図形内に描きこみましょう。
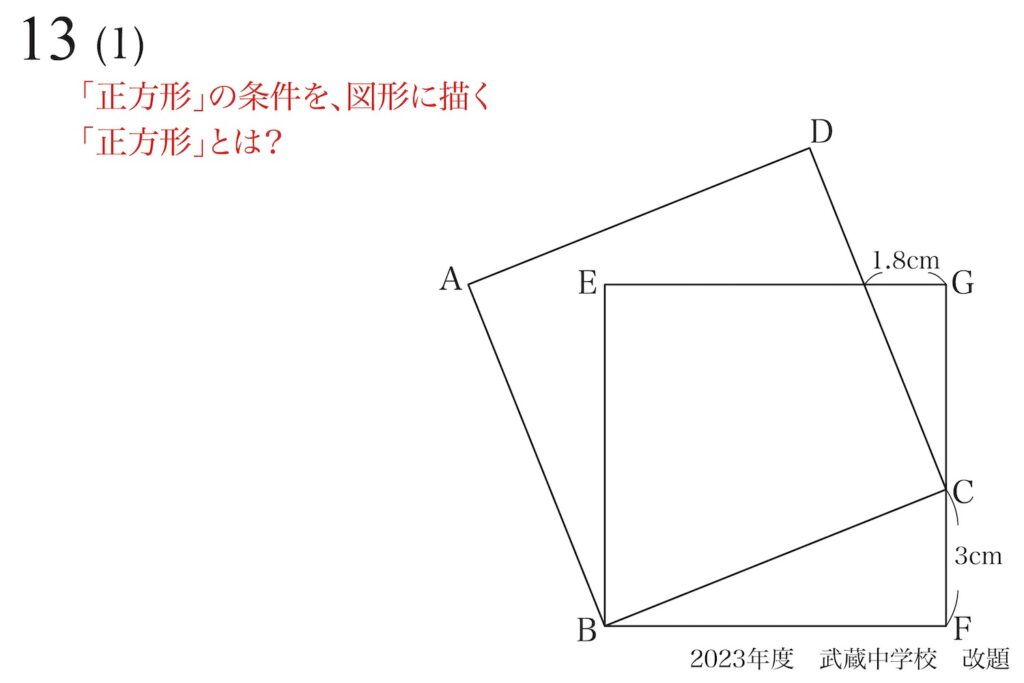

「正方形とは?」をしっかり考えましょう。
・全ての辺が同じ長さ
・全ての角が同じで直角



これは
分かるよ!
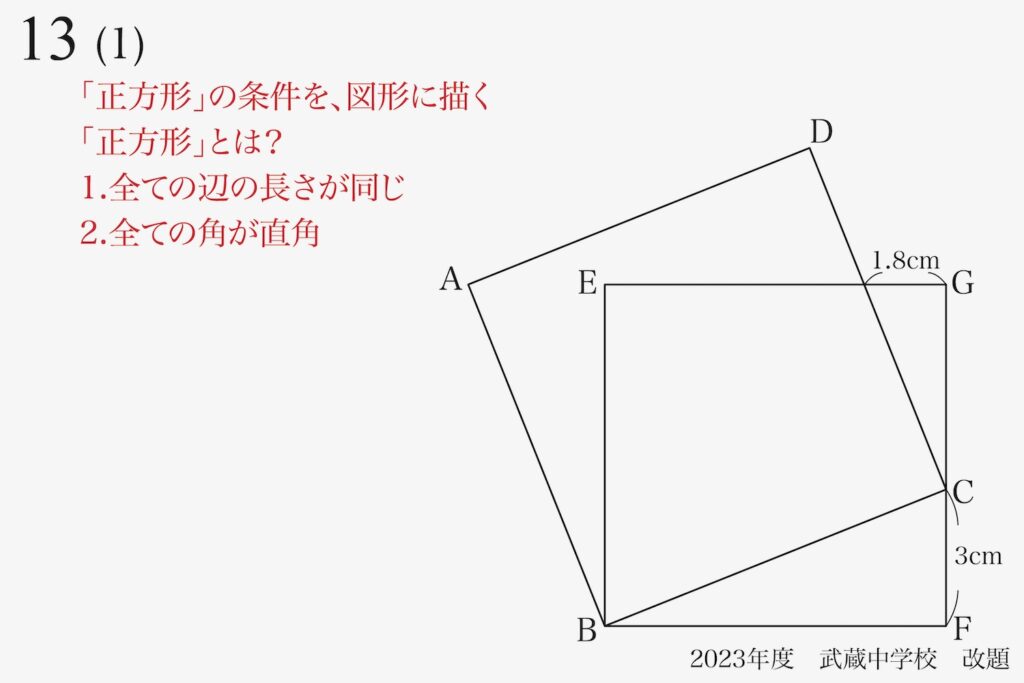

正方形は「二つの大事な性質」がある非常にシンプルな四角形です。


工作で使う方眼紙は「多数の正方形でできている」用紙です。
いわば「正方形は全ての図形の基本となる図形」です。
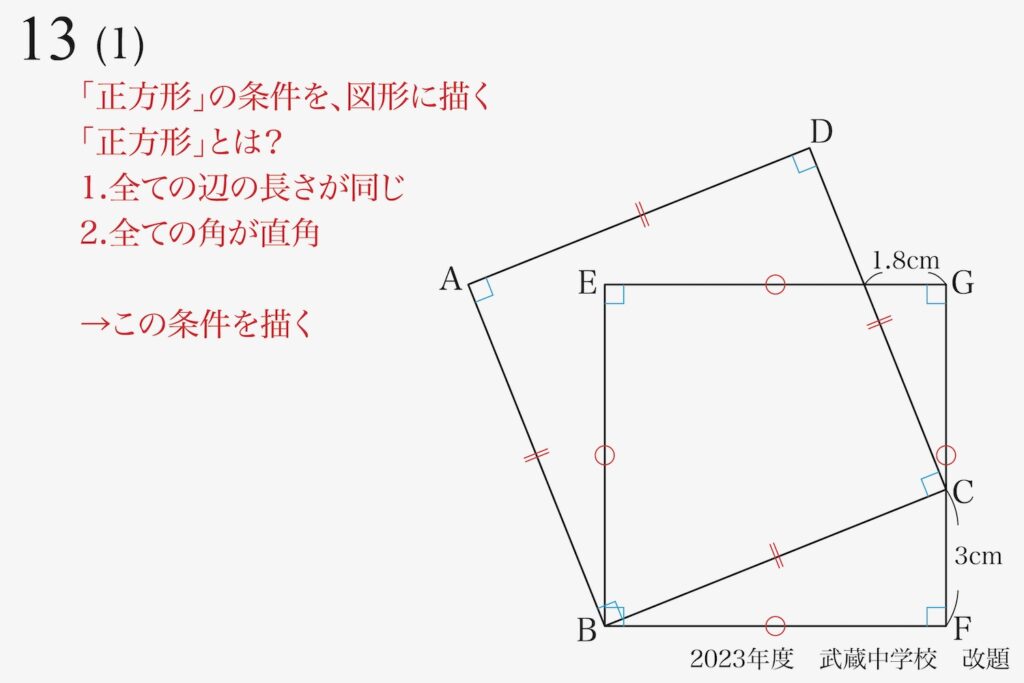

「基本的図形」である正方形。
改めて見ると、非常に美しいです、
まず「全ての辺の長さが同じ」と「全ての角が直角」の条件を上の図のように描いてみましょう。
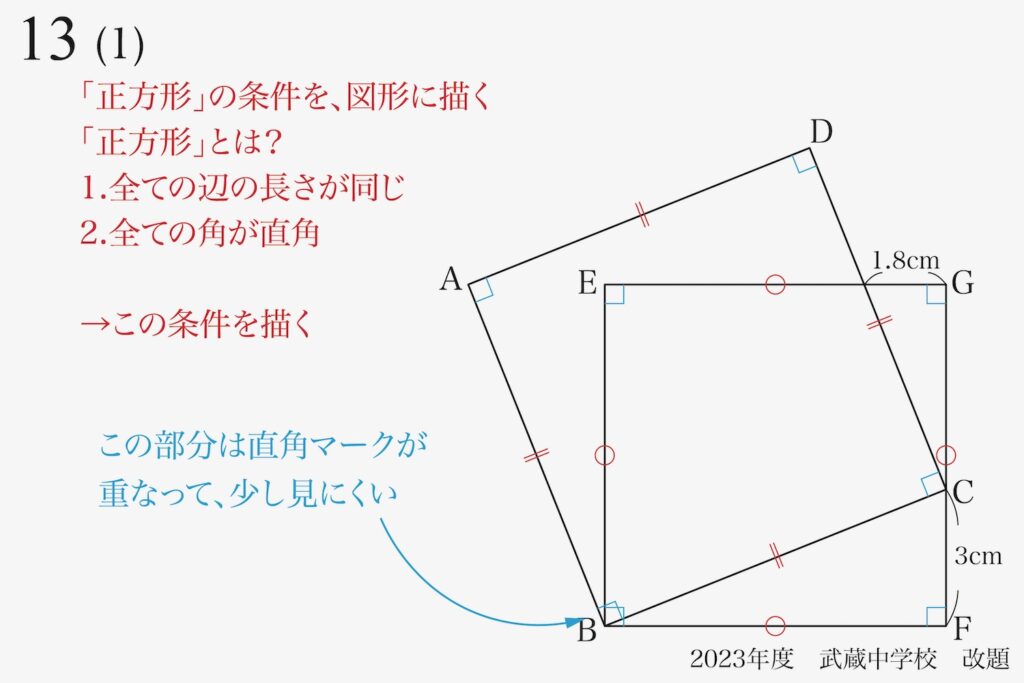

この時、Bの周辺のように「直角マーク」などが「重なって見えずらい」時があります。
これに対しては「描く」「描かない」は本人次第です。
僕は「描いた方が良い」と考えます。
これで、問題の条件が「全て視覚化された」状況になりました。
・問題の条件を全て描きこむ:同じ長さ・同じ角度など
・図形の性質などを描く過程で、条件を頭で整理するので解きやすくなる



確かに、こうして
描きこんだ方が分かる気がする・・・



「全部わかっていること」なのに、
「描いた方が分かる」って不思議・・・
本問を「考えても、出来なかった」方はこの「条件を視覚化した」状況で再度トライしてみましょう。
出来た方も「図形問題への基本姿勢」をしっかり固めましょう。
算数の学力を上げるためには、こうした「基本姿勢」をしっかり身につけることが非常に大事です。
次回は下記リンクです。





