前回は「文章題のてんびん算のコツ・ポイント〜3つのてんびん算・食塩水を混ぜる・状況を絵に描いて整理・食塩と「混ぜて半分」の算数的意味・状況を算数的視点で考える・問題 12〜」の話でした。
問題 12

問題の内容を図や絵に描いて理解:記述式や解く過程を示すとき
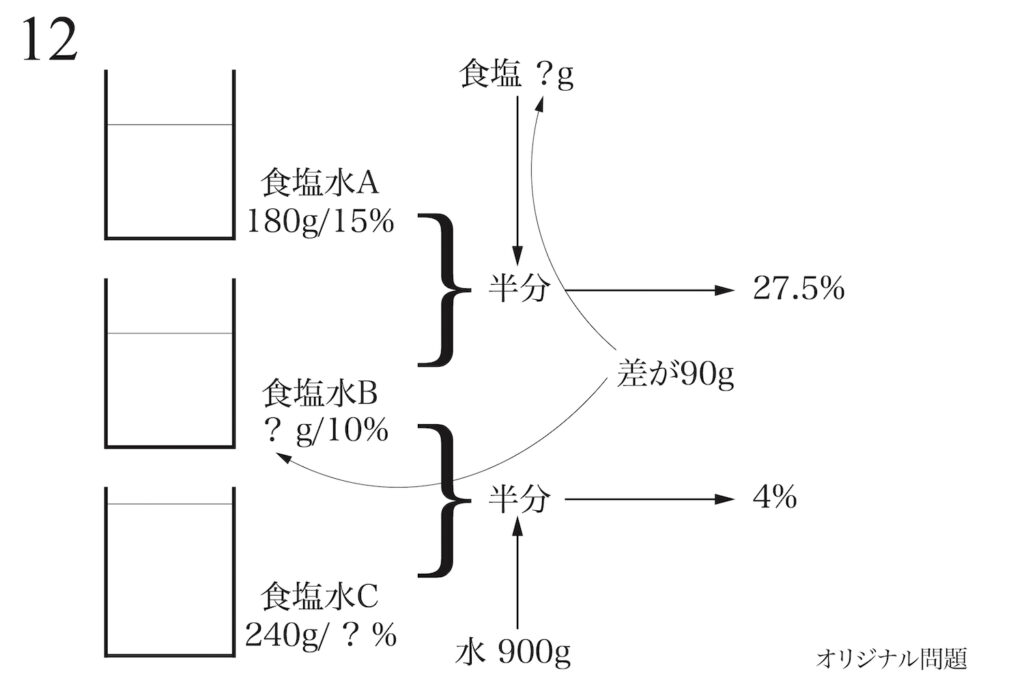
少し文章が長い文章題です。
・文章の内容を理解することが大変
・いくつかの量や長さが登場するので、混乱することがある
文章が長い文章題は、状況をしっかり理解することが問題を解く第一歩です。
ここで「しっかり理解」があやふやだと、分からなくなってしまう可能性があります。
・状況を簡単な絵や図に描く
・状況をしっかり理解することが解く第一歩
・大事な量や長さなどを見落とさない
問題文の余白に「メモ」や「走り書き」でも良いので、上のような図や絵を描くようにしましょう。
 男子小学生
男子小学生こうやって
整理すると、分かりやすいね!



文章より、
断然分かる!
麻布中・武蔵中などの記述式では、上のような絵を描くことが大事です。
このような絵が描かれていると、採点者は、



問題を
よく理解しているな・・・
こう考えて、途中で終わっていても、



ここまでは、
よく出来ている・・・
このように判断して、ある程度の点数を与えるでしょう。
「解く過程を書きなさい」という形式の問題でも書いても良いですが、余白とのバランスによります。



私の志望校は
「解く過程を書きなさい」が多いけど・・・



描く部分は、それほど大きくなくて、
計算式を書いたら、一杯かも・・・
「書く余白」がなくなってしまっては困ります。
上のような図・絵を答案に書けない時は、問題文の余白に「ササッと描いて理解」しましょう。
「混ぜて半分」を描いて考える
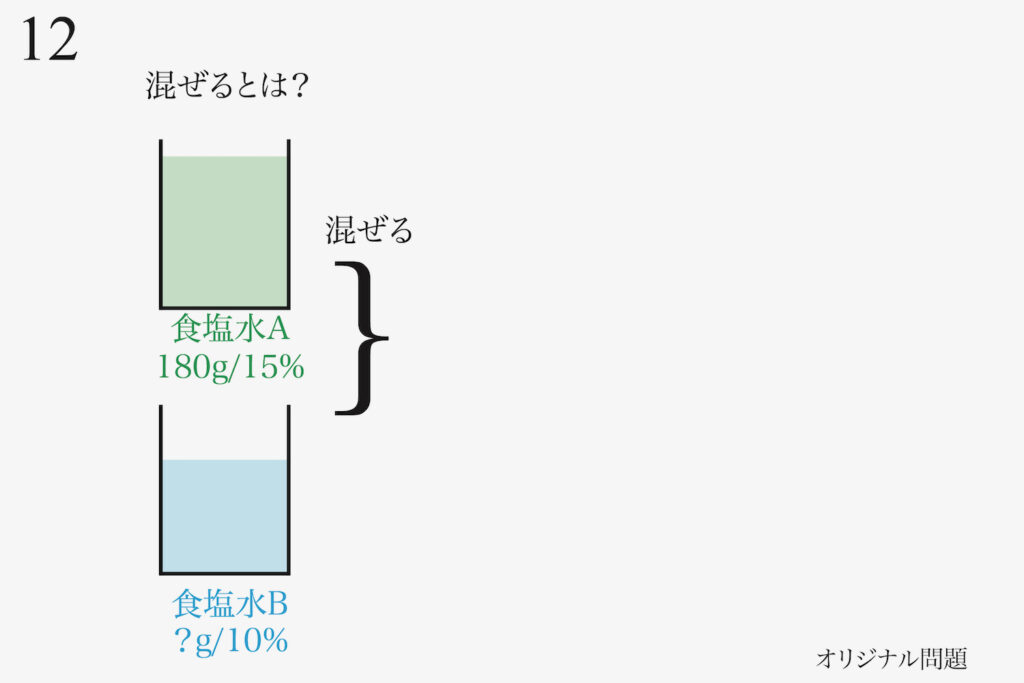

この問題では、「二つの食塩水を混ぜて、半分」がポイントです。
実際に二つの食塩水A、Bを混ぜる状況を描いてみましょう。



これは、描かなくても
分かるよ!
「描かなくても分かる」かもしれませんが、描いてみましょう。
濃度・重さ共に分かっている食塩水Aと、濃度のみ分かっている食塩水Bを混ぜます。
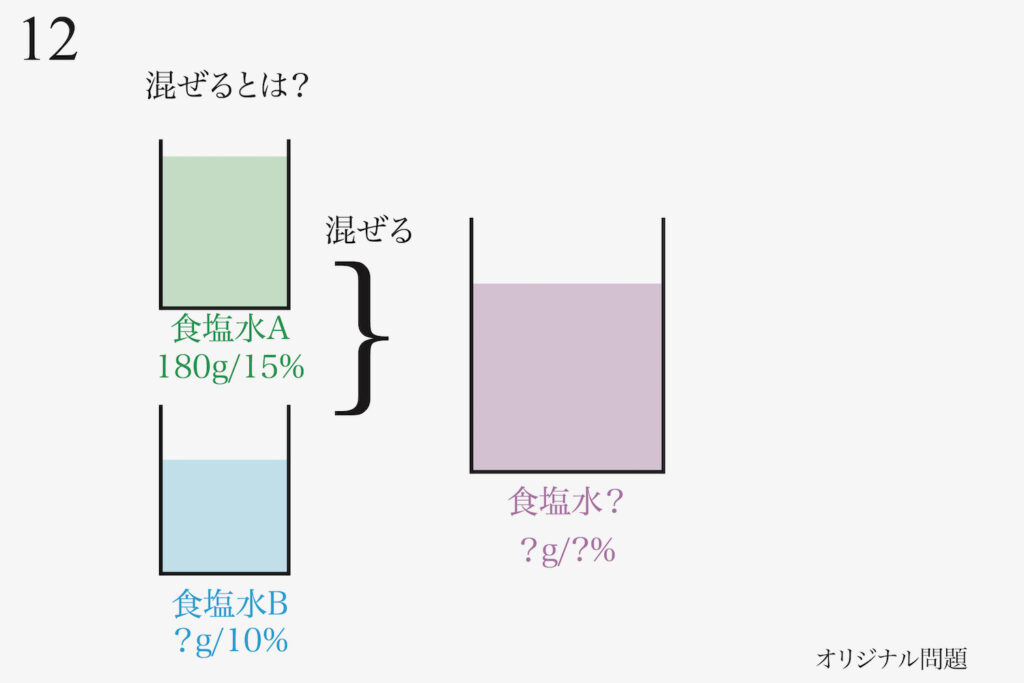

これらを混ぜると、「濃度も重さも分からない食塩水」となります。



濃度も重さも分からない
食塩水って・・・



どう考えたら
いいの?
「濃度も重さも分からない食塩水」を半分にします。
すると、その食塩水もまた「濃度も重さも分からない食塩水」となります。



これでは
困ってしまうけど・・・
てんびん算の意味:混ぜる食塩水と理科的視点

ここから、てんびん算で考えてみましょう。
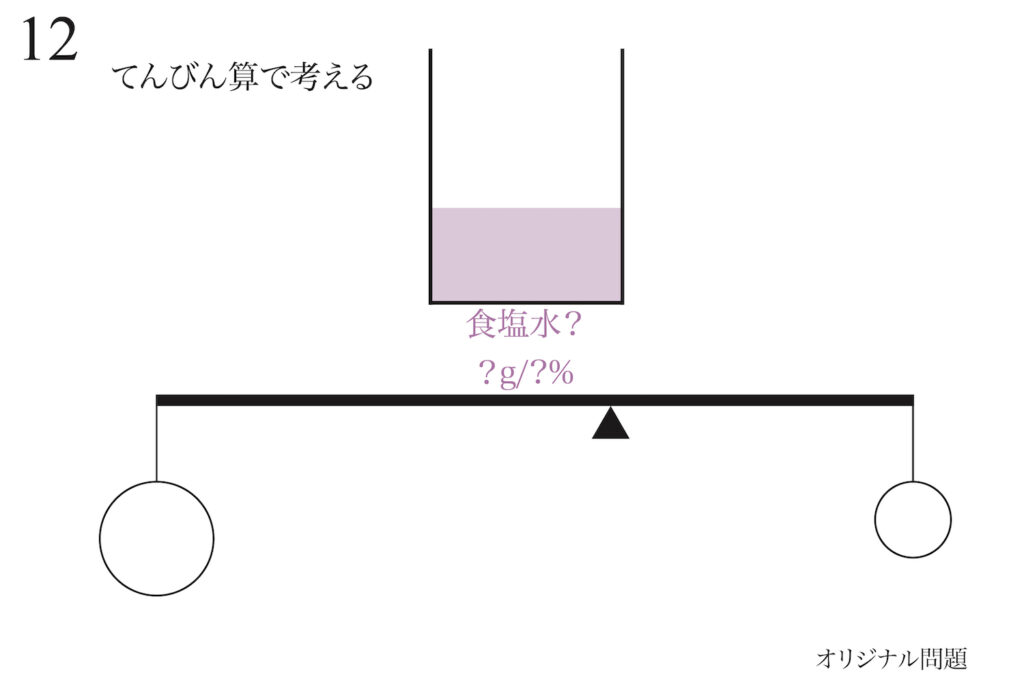

食塩水Aと食塩水Bを混ぜた食塩水を考えます。
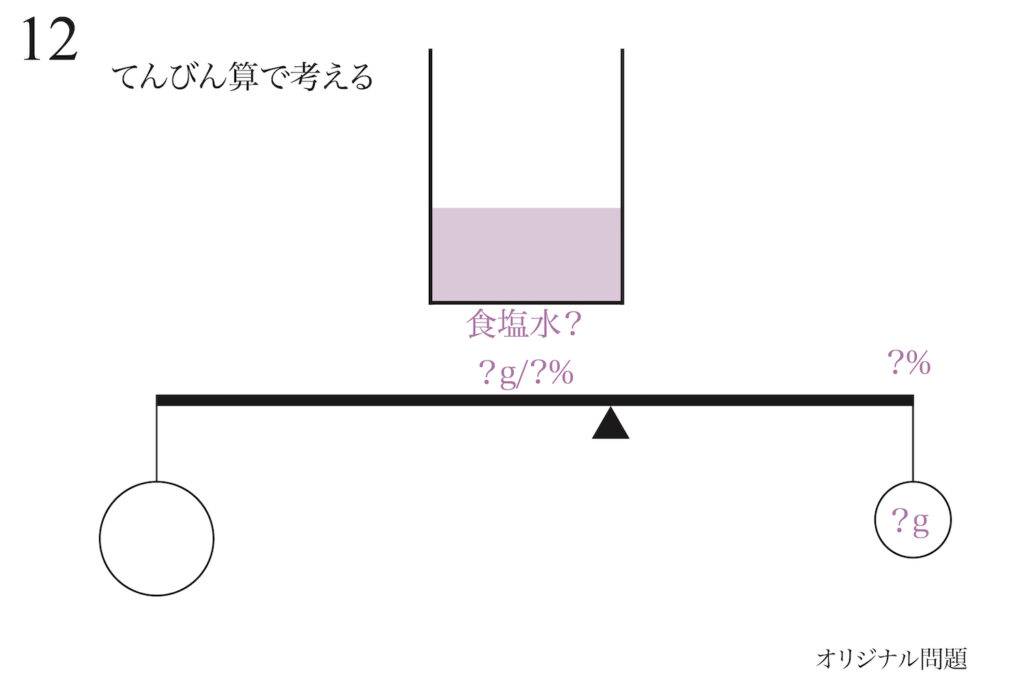

重さも濃度も分かりません。



これって、
てんびんになるの?
この重さ・濃度の分からない食塩水を、なんとか「てんびん」で考えられないでしょうか。



これって、
無理じゃない?


やはり、重さ・濃度のどちらかは分かってないと、難しそうです。



無理だよ・・・
全然分からないよ・・・
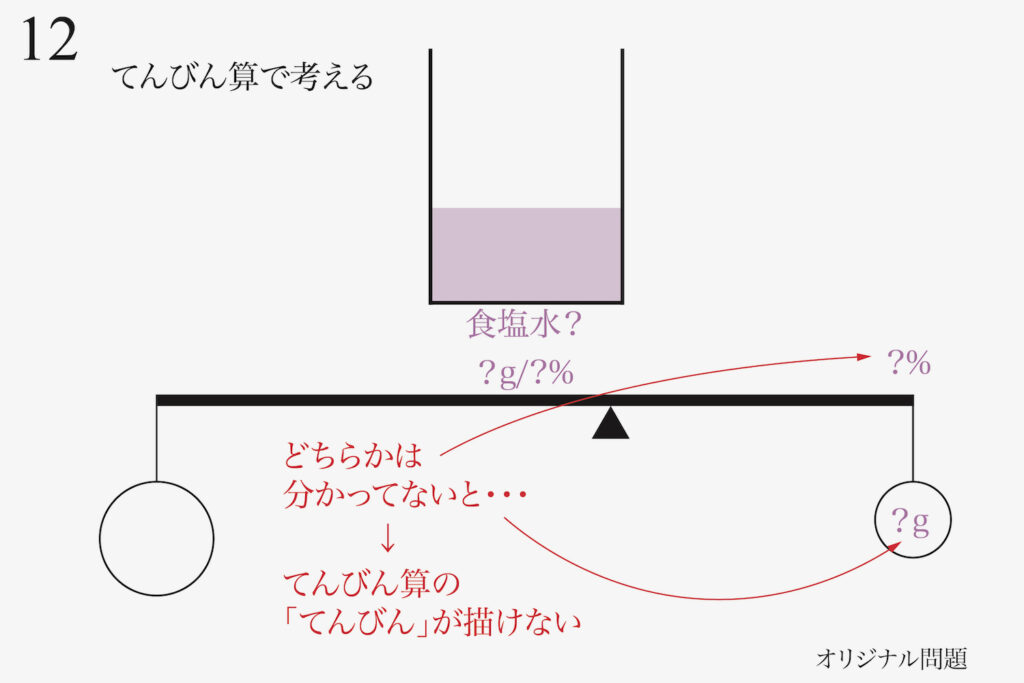

それは、「てんびん」をうまく描けず、モーメント(回転する力)を考えることが出来ないからです。
てんびん算は「理科と算数の架け橋」でもあります。
算数の問題ですが、食塩水やてんびん算を考えるときは、理科的発想を考えましょう。


上皿てんびんを考えるとき、分銅の重さも上皿の位置も不明だと困ります。
上皿てんびんの「上皿の位置」は固定で「両側一緒」ですが、てんびん算では、ここが動きます。
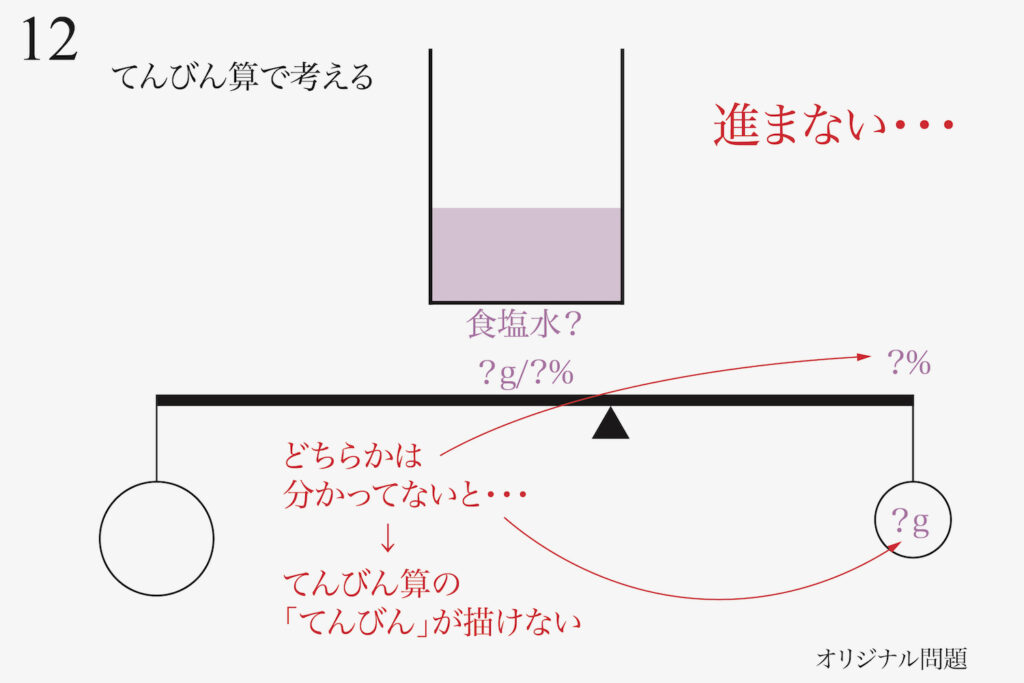

ここで困ってしまい、手が止まってしまいます。



てんびん算では、
解けないんじゃないの?
方程式で立式して考えても良いですが、もう少してんびん算で考えましょう。
「混ぜて半分」の算数的意味:食塩水=食塩+水
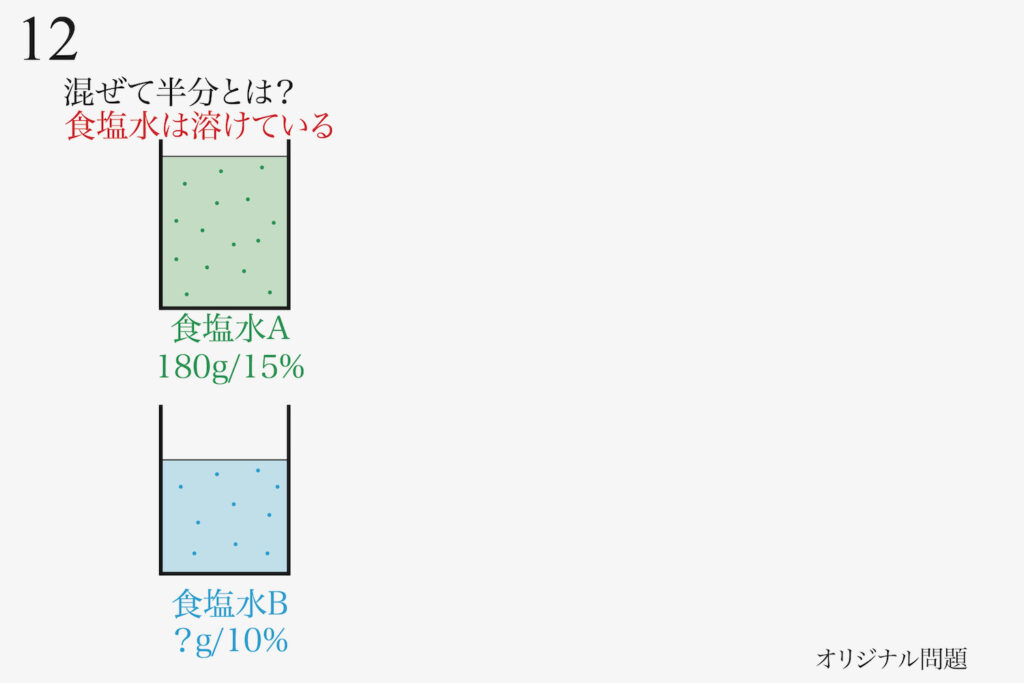

食塩水は、水に食塩が溶けた水溶液です。
文字通り「食塩水=食塩+水」なのです。
溶けている食塩水を、上の絵のように鉛筆や色鉛筆で点を打ってみましょう。
そして、具体的に「食塩があるイメージ」を考えましょう。
実際には食塩は「溶けている」ので、目では見えません。
実際には、食塩水には「食塩はいる」のです。
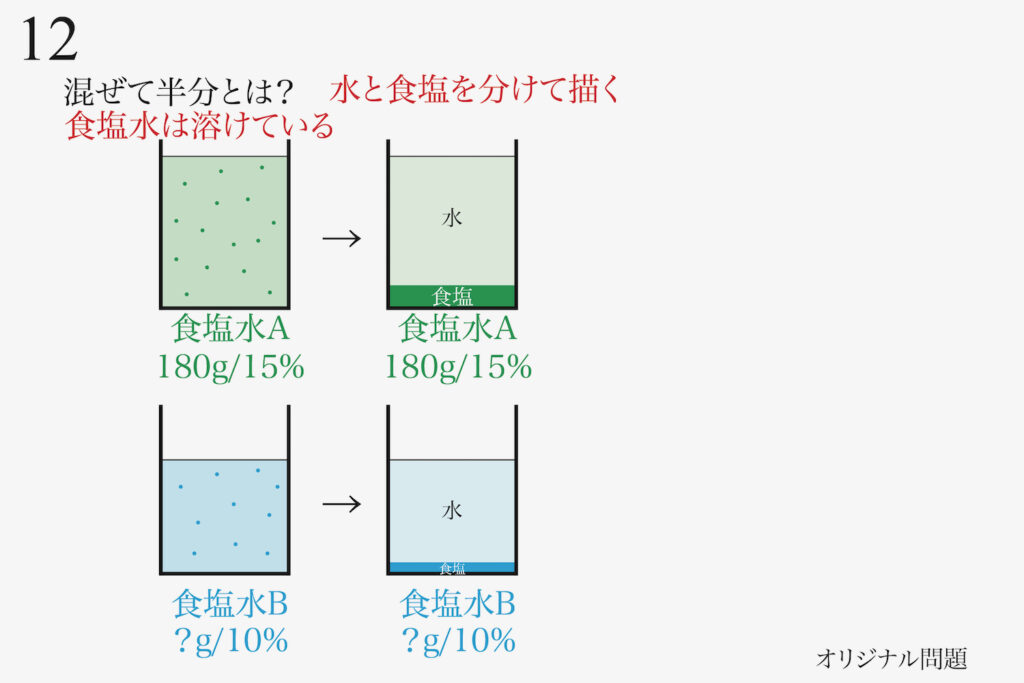

それら食塩と水を分離して描いてみましょう。
実際に、このように「食塩が沈澱する状況」ではありません。



「違う」のでは、
意味ないんじゃない?
「食塩が沈澱していない」状況ですが、「食塩水の実態」をこのように考えてみましょう。



なんとなく
分かるけど、これで解けるの?
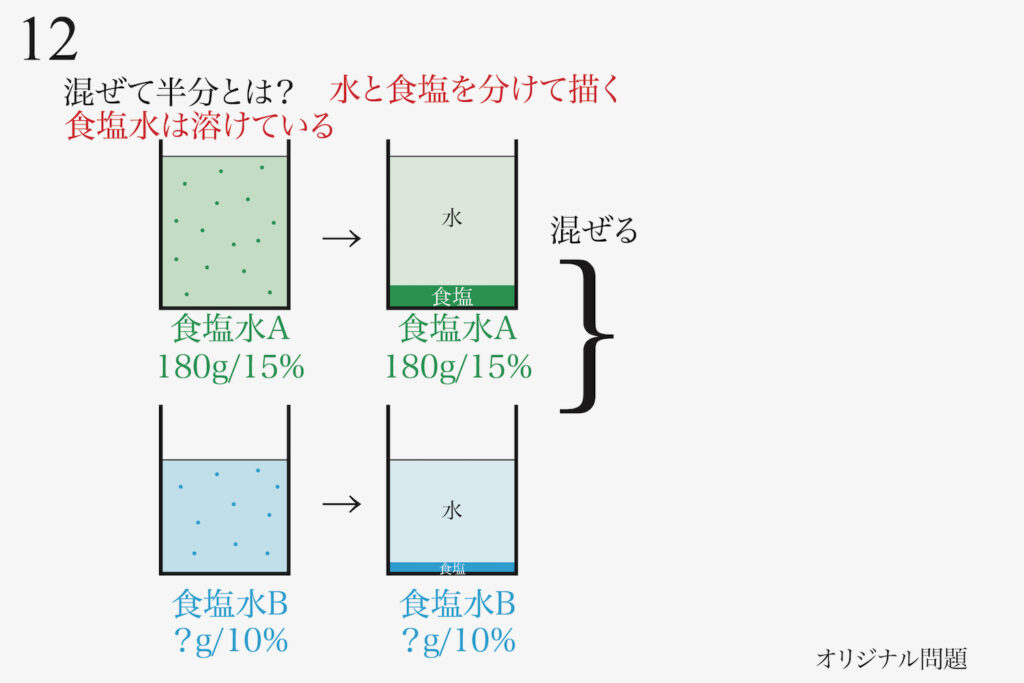

そして、「食塩水A=Aの水+Aの食塩」と考えます。
「食塩水B=Bの水+Bの食塩」です。
「二つの食塩水を混ぜる」のですが、これらの「二つの食塩と水のセットを混ぜる」と考えましょう。
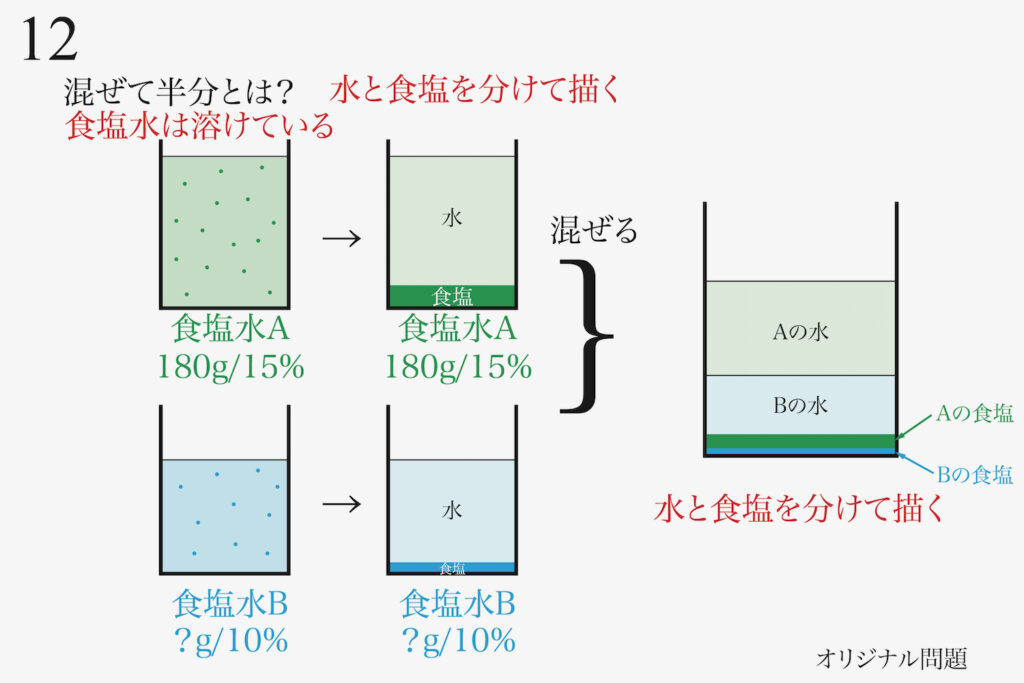

そして、混ぜた後も「食塩が水に溶けている」のですが、別々に分離して描いてみます。
この地層のように積み重なった「食塩+水」が「食塩水Aと食塩水Bを混ぜた食塩水」の実態です。
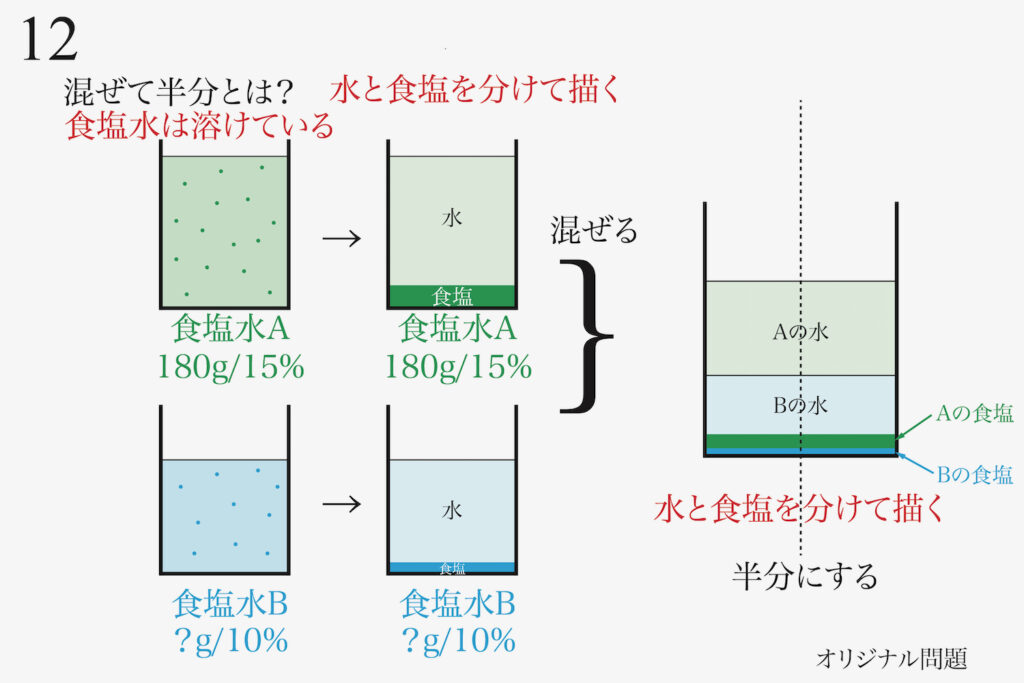

この「AとBを混ぜた食塩水」を半分にするので、縦に半分にする線を描いてみましょう。



あっ!
そういうことかな。
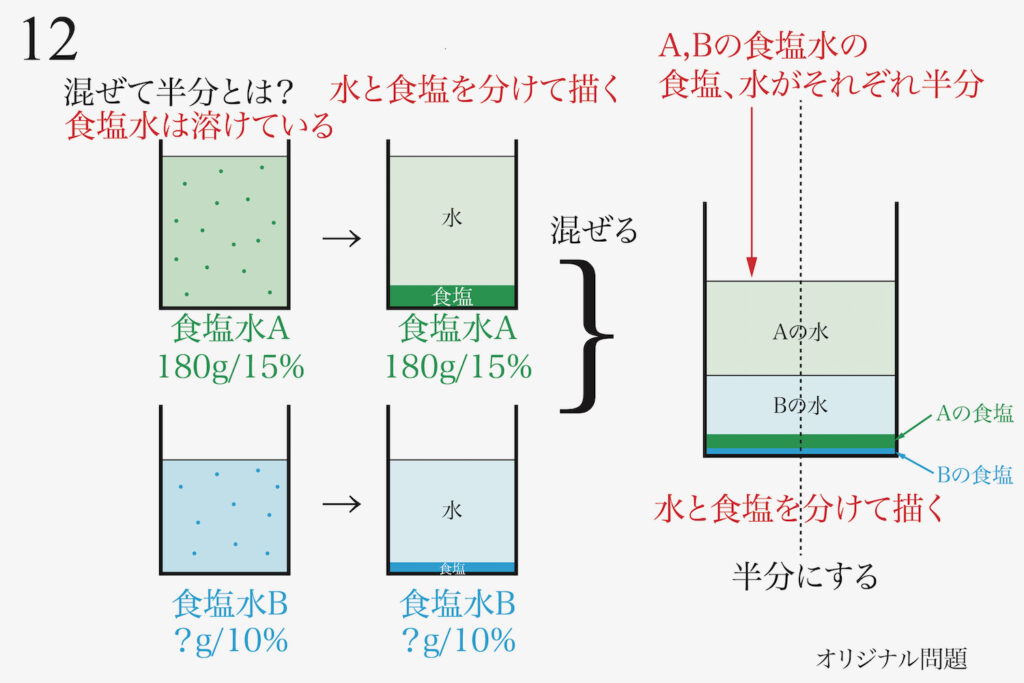

「AとBを混ぜた食塩水」は「A,Bの食塩水の食塩、水がそれぞれ半分入っている」のが実態です。



これは、
分かりやすい!
これで、この問題のポイントが分かりました。
・混ぜる前の食塩水を「それぞれ半分にして混ぜる」と同じ
・食塩と水が分離したイメージで描いて考える
食塩水の問題をみて、すぐに立式したり、天秤を描くよりも前にすることがあります。
それは、一度状況をしっかり整理して考えることです。
「混ぜる」などの問題の時は、上の絵のように「混ぜる状況」を自分で描いてみましょう。
上記リンクでは、「描いて考える」学び方をご紹介しています。
途中でうまくいかなかった方は、もう一度ここで本問を考えてみましょう。
次回は下記リンクです。



